数学人教A版(2019)选择性必修第二册4.3.1等比数列的概念及通项公式(共26张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第二册4.3.1等比数列的概念及通项公式(共26张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 15:34:14 | ||
图片预览






文档简介
(共26张PPT)
4.3.1等比数列的概念及通项公式
人教A版(2019)
选择性必修第二册
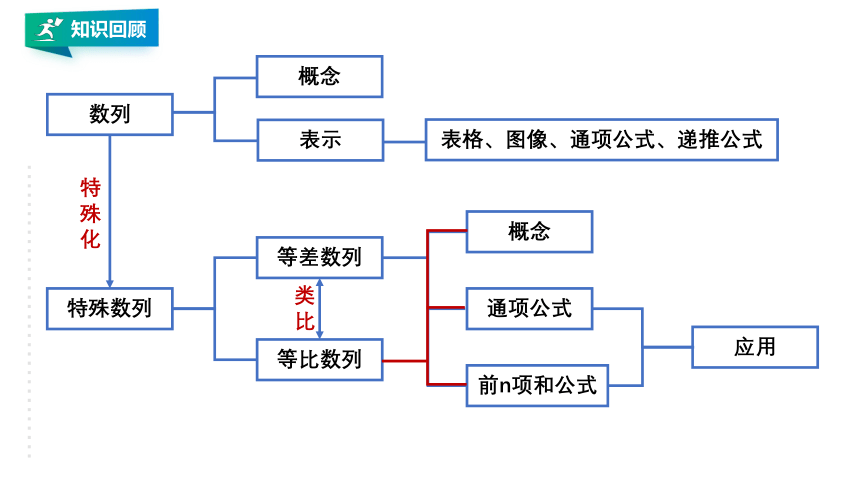
知识回顾
特殊数列
等差数列
等比数列
概念
通项公式
前n项和公式
应用
数列
概念
表示
表格、图像、通项公式、递推公式
特殊化
类比
观察与思考
类比等差数列的研究,从运算的角度,观察下列数列有什么共同规律?
两河流域发掘的古巴比伦时期的泥板上记录了下面的数列:
①;②;.
2.《庄子 天下》中提到:“一尺之棰,日取其半,万世不竭.”若把“一尺之棰”的长度看
成 “1”,那么从第1天起,各天得到的“棰”的长度依次是. ④
3. 在营养和生存空间没有限制的情况下,某种细菌每20min就通过分裂繁殖一代,那么一
个这种细菌从第1次分裂开始,各次分裂产生的后代个数是2,4,8,16,32,64,… ⑤
4. 某人存入银行a元,存期为5年,年利率为r,那么按照复利,他5年内每年末得到的本利
和分别是⑥
从第二项起,每一项与它的前一项的比都等于同一个常数.
新知讲解
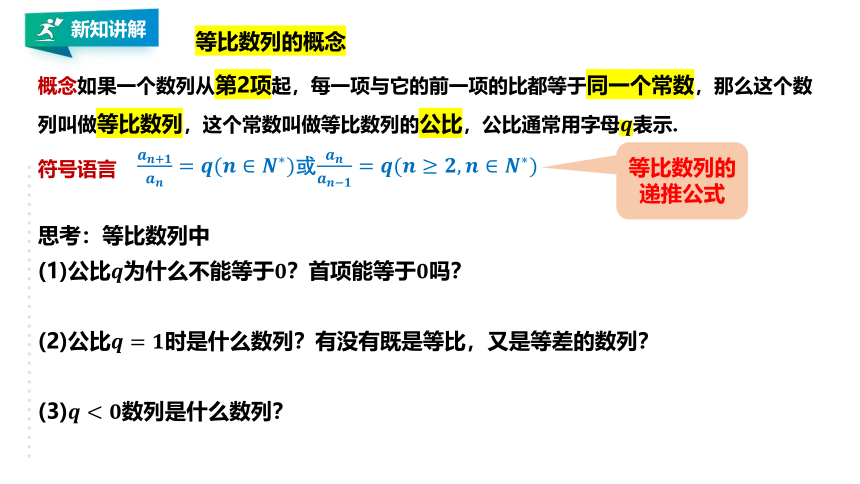
等比数列的概念
概念如果一个数列从第2项起,每一项与它的前一项的比都等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母表示.
符号语言
或
等比数列的递推公式
思考:等比数列中
(1)公比为什么不能等于?首项能等于吗?
(2)公比时是什么数列?有没有既是等比,又是等差的数列?
(3)数列是什么数列?
新知讲解
等比中项
与等差中项类似,如果在a 和中间插入一个数,使成等比数列,那么叫做与的等比中项. 此时 .
概念辨析(对的打“A”,错的打“B”)
(1)若数列那么是等比数列. ()
(2)数列中,已知,,那么是等比数列. ()
(3)常数列一定为等比数列. ()
(4)任意两个非零常数都有等比中项. ()
成等比数列的充要条件. ( )
B
B
B
B
B
课堂练习
B
课堂练习
2.已知,,成等差数列,,,成等比数列,则______.
3.“”是“,,,成等比数列”的(@3@)
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
B
合作探究
等比数列的通项公式
探究已知一个等比数列的首项为,公比为,试根据等比数列的定义推导它的通项公式?
又a1=a1q0=a1q1-1,即当n=1时上式也成立.
方法1由等比数列的定义可得:
a2=a1q
a3=a2q = (a1q) q = a1q2,
a4=a3q = (a1q2) q =a1q3,
an=a1qn-1 ( n ≥2 ) .
则首项为a1,公比为q的等比数列{an}通项公式为
an=a1qn-1 (n∈)
不完全
归纳法
合作探究
等比数列的通项公式
探究已知一个等比数列的首项为,公比为,试根据等比数列的定义推导它的通项公式?
……
方法2由等比数列的定义得
n-1个
9
又a1=a1q0=a1q1-1,即当n=1时上式也成立.
则首项为a1,公比为q的等比数列{an}通项公式为
an=a1qn-1 (n∈)
累乘法
新知讲解
首项为,公比为的等比数列的通项公式为
反之,任给指数函数且构成一个等比数列,其首项为,公比为.
类似于一次函数与等差数列的关系,
由可知,当q>0 且时的函数值,
例题讲解
等比数列的通项公式的应用
例1 若等比数列的第4项和第6项分别为48和12,求的第5项.
解法1由 ,得
②的两边分别除以①的两边,得
即
当时,
当时,
因此,的第5项是24或-24.
解法2因为 是与的等比中项,
所以
所以
例题讲解
例2 已知等比数列的公比为q,试用的第m项表示 .
解:由题意,得
②的两边分别除以①的两边,得
所以
等比数列的任意一项都可以由该数列的某一项和公比表示.
等比数列通项公式的推广
例题讲解
解:设前三项的公比为q,后三项的公差为d,则数列的各项依次为
解方程组,得或
所以这个数列是20,40,80,96,112 或180,120,80,16,-48 .
例3 数列共有5项,前三项成等比数列,后三项成等差数列,第3项等于80,第2项与第4项的和等于136,第1项与第5项的和等于132.求这个数列.
1(教材P31T5改编)已知数列是等比数列,下列说法错误的是()
a3 , a5,a7 成等比数列
a1 , a3,a9 成等比数列
an , an+1,an+2 成等比数列
n>3时,an-3 , an ,an+3 成等比数列
课堂练习
B
②在等比数列中,若m+n=p+q(),则
①在等比数列中,当 m+n=2k()时,;
拓展(等比数列的运算性质)
特别地,等比数列中,
课堂练习
2.已知是首项为1,公比为3的等比数列,则.
4.在等比数列中,,,,求.
3.如果,,,,成等比数列,那么
6.已知为等比数列,,,则(@4@)
A.B.C.D.
5.若
课堂总结
1. 等比数列的概念;
2.等比数列通项公式及其推广;
3. 等比中项;
4. 等比数列与指数函数的关系;
5.等比数列通项的性质.
例题讲解
例4 已知数列的首项 .
(1)若为等差数列,公差d=2,证明数列为等比数列;
(2)若等比数列,公比为 ,证明数列为等差数列.
证明:(1)由, d=2,得的通项公式为 .
设,则
又
所以,是以27为首项,9为公比的等比数列.
例题讲解
证明:(2)由, ,得
两边取以3为底的对数,得
所以
又24
所以,是首项为1,公差为-2的等差数列.
例4 已知数列的首项 .
(1)若为等差数列,公差d=2,证明数列为等比数列;
(2)若等比数列,公比为 ,证明数列为等差数列.
方法总结
证明数列是等比数列的常用的方法
1.定义法:(为常数且)或(为常数且)
为等比数列.
2.等比中项法:为等比数列.
课堂练习
练习1.在数列中,若,且 . 证明:数列是等比数列.
证明:[定义法]∵,∴
又∵,
∴.
∴数列是首项为,公比为2等比数列.
课堂练习
练习1.在数列中,若,且 . 证明:数列是等比数列.
证明:[等比中项法]∵,∴
又∵,∴.
∴.
即,,成等比数列,
∴数列是等比数列.
课堂练习
2.已知数列的前项和,求证:是等比数列,并求出通项公式.
证明:∵∴
∴.
∴
又∵.
又由知,知
∴,∴是以为首项,为公比的等比数列.
其通项公式.
例题讲解
等比数列的通项公式在实际问题中的应用
例5 用10 000 元购买某个理财产品一年.
(1)若以月利率0.400%的复利计息,12个月能获得多少利息(精确到1元)?
(2)若以季度复利计息,存4个季度,则当每季度利率为多少时,按季结算的利息不少于按月结算的利息(精确到)?
解:(1)设这笔钱存n个月以后的本利和组成一个数列,
则是等比数列,首项,公比q=1+0.400% ,
所以
所以,12个月后的利息为(元)
例题讲解
(2)设季度利率为r,这笔钱存n个季度以后的本金和组成一个数列,
则也是一个等比数列,首项,公比为1+r,
于是
因此,以季度复利计息,存4个季度后的利息为 元.
解不等式,得
所以,当季度利率不小于1.206%时,按季结算的利息不少于按月结算的利息.
例5 用10 000 元购买某个理财产品一年.
(1)若以月利率0.400%的复利计息,12个月能获得多少利息(精确到1元)?
(2)若以季度复利计息,存4个季度,则当每季度利率为多少时,按季结算的利息不少于按月结算的利息(精确到)?
例题讲解
例6 某工厂去年12月试产1050个高新电子产品,产品合格率为90%. 从今年1月开始,工厂在接下来的两年中将生产这款产品. 1月按去年12月的产量和产品合格率生产,以后每月的产量都在前一个月的基础上提高5%,产品合格率比前一个月增加0.4%,那么生产该产品一年后,月不合格品的数量能否控制在100个以内?
例题讲解
解:设从今年1月起,各月的产量及不合格率分别构成数列,.
,
,其中,n=1,2,…,24,
则从今年1月起,各月不合格产品的数量是
由,得
所以,当时,递减,又
所以,当时,
所以,生产该产品一年后,月不合格品的数量能控制在100以内.
4.3.1等比数列的概念及通项公式
人教A版(2019)
选择性必修第二册
知识回顾
特殊数列
等差数列
等比数列
概念
通项公式
前n项和公式
应用
数列
概念
表示
表格、图像、通项公式、递推公式
特殊化
类比
观察与思考
类比等差数列的研究,从运算的角度,观察下列数列有什么共同规律?
两河流域发掘的古巴比伦时期的泥板上记录了下面的数列:
①;②;.
2.《庄子 天下》中提到:“一尺之棰,日取其半,万世不竭.”若把“一尺之棰”的长度看
成 “1”,那么从第1天起,各天得到的“棰”的长度依次是. ④
3. 在营养和生存空间没有限制的情况下,某种细菌每20min就通过分裂繁殖一代,那么一
个这种细菌从第1次分裂开始,各次分裂产生的后代个数是2,4,8,16,32,64,… ⑤
4. 某人存入银行a元,存期为5年,年利率为r,那么按照复利,他5年内每年末得到的本利
和分别是⑥
从第二项起,每一项与它的前一项的比都等于同一个常数.
新知讲解
等比数列的概念
概念如果一个数列从第2项起,每一项与它的前一项的比都等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母表示.
符号语言
或
等比数列的递推公式
思考:等比数列中
(1)公比为什么不能等于?首项能等于吗?
(2)公比时是什么数列?有没有既是等比,又是等差的数列?
(3)数列是什么数列?
新知讲解
等比中项
与等差中项类似,如果在a 和中间插入一个数,使成等比数列,那么叫做与的等比中项. 此时 .
概念辨析(对的打“A”,错的打“B”)
(1)若数列那么是等比数列. ()
(2)数列中,已知,,那么是等比数列. ()
(3)常数列一定为等比数列. ()
(4)任意两个非零常数都有等比中项. ()
成等比数列的充要条件. ( )
B
B
B
B
B
课堂练习
B
课堂练习
2.已知,,成等差数列,,,成等比数列,则______.
3.“”是“,,,成等比数列”的(@3@)
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
B
合作探究
等比数列的通项公式
探究已知一个等比数列的首项为,公比为,试根据等比数列的定义推导它的通项公式?
又a1=a1q0=a1q1-1,即当n=1时上式也成立.
方法1由等比数列的定义可得:
a2=a1q
a3=a2q = (a1q) q = a1q2,
a4=a3q = (a1q2) q =a1q3,
an=a1qn-1 ( n ≥2 ) .
则首项为a1,公比为q的等比数列{an}通项公式为
an=a1qn-1 (n∈)
不完全
归纳法
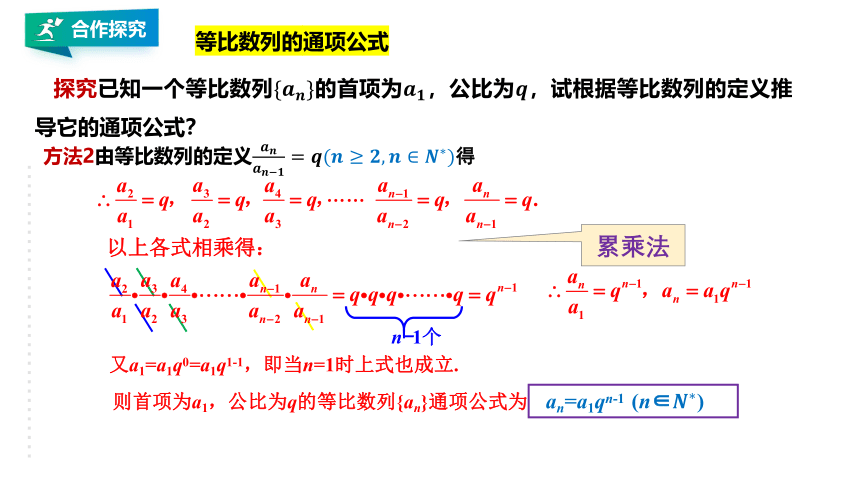
合作探究
等比数列的通项公式
探究已知一个等比数列的首项为,公比为,试根据等比数列的定义推导它的通项公式?
……
方法2由等比数列的定义得
n-1个
9
又a1=a1q0=a1q1-1,即当n=1时上式也成立.
则首项为a1,公比为q的等比数列{an}通项公式为
an=a1qn-1 (n∈)
累乘法
新知讲解
首项为,公比为的等比数列的通项公式为
反之,任给指数函数且构成一个等比数列,其首项为,公比为.
类似于一次函数与等差数列的关系,
由可知,当q>0 且时的函数值,
例题讲解
等比数列的通项公式的应用
例1 若等比数列的第4项和第6项分别为48和12,求的第5项.
解法1由 ,得
②的两边分别除以①的两边,得
即
当时,
当时,
因此,的第5项是24或-24.
解法2因为 是与的等比中项,
所以
所以
例题讲解
例2 已知等比数列的公比为q,试用的第m项表示 .
解:由题意,得
②的两边分别除以①的两边,得
所以
等比数列的任意一项都可以由该数列的某一项和公比表示.
等比数列通项公式的推广
例题讲解
解:设前三项的公比为q,后三项的公差为d,则数列的各项依次为
解方程组,得或
所以这个数列是20,40,80,96,112 或180,120,80,16,-48 .
例3 数列共有5项,前三项成等比数列,后三项成等差数列,第3项等于80,第2项与第4项的和等于136,第1项与第5项的和等于132.求这个数列.
1(教材P31T5改编)已知数列是等比数列,下列说法错误的是()
a3 , a5,a7 成等比数列
a1 , a3,a9 成等比数列
an , an+1,an+2 成等比数列
n>3时,an-3 , an ,an+3 成等比数列
课堂练习
B
②在等比数列中,若m+n=p+q(),则
①在等比数列中,当 m+n=2k()时,;
拓展(等比数列的运算性质)
特别地,等比数列中,
课堂练习
2.已知是首项为1,公比为3的等比数列,则.
4.在等比数列中,,,,求.
3.如果,,,,成等比数列,那么
6.已知为等比数列,,,则(@4@)
A.B.C.D.
5.若
课堂总结
1. 等比数列的概念;
2.等比数列通项公式及其推广;
3. 等比中项;
4. 等比数列与指数函数的关系;
5.等比数列通项的性质.
例题讲解
例4 已知数列的首项 .
(1)若为等差数列,公差d=2,证明数列为等比数列;
(2)若等比数列,公比为 ,证明数列为等差数列.
证明:(1)由, d=2,得的通项公式为 .
设,则
又
所以,是以27为首项,9为公比的等比数列.
例题讲解
证明:(2)由, ,得
两边取以3为底的对数,得
所以
又24
所以,是首项为1,公差为-2的等差数列.
例4 已知数列的首项 .
(1)若为等差数列,公差d=2,证明数列为等比数列;
(2)若等比数列,公比为 ,证明数列为等差数列.
方法总结
证明数列是等比数列的常用的方法
1.定义法:(为常数且)或(为常数且)
为等比数列.
2.等比中项法:为等比数列.
课堂练习
练习1.在数列中,若,且 . 证明:数列是等比数列.
证明:[定义法]∵,∴
又∵,
∴.
∴数列是首项为,公比为2等比数列.
课堂练习
练习1.在数列中,若,且 . 证明:数列是等比数列.
证明:[等比中项法]∵,∴
又∵,∴.
∴.
即,,成等比数列,
∴数列是等比数列.
课堂练习
2.已知数列的前项和,求证:是等比数列,并求出通项公式.
证明:∵∴
∴.
∴
又∵.
又由知,知
∴,∴是以为首项,为公比的等比数列.
其通项公式.
例题讲解
等比数列的通项公式在实际问题中的应用
例5 用10 000 元购买某个理财产品一年.
(1)若以月利率0.400%的复利计息,12个月能获得多少利息(精确到1元)?
(2)若以季度复利计息,存4个季度,则当每季度利率为多少时,按季结算的利息不少于按月结算的利息(精确到)?
解:(1)设这笔钱存n个月以后的本利和组成一个数列,
则是等比数列,首项,公比q=1+0.400% ,
所以
所以,12个月后的利息为(元)
例题讲解
(2)设季度利率为r,这笔钱存n个季度以后的本金和组成一个数列,
则也是一个等比数列,首项,公比为1+r,
于是
因此,以季度复利计息,存4个季度后的利息为 元.
解不等式,得
所以,当季度利率不小于1.206%时,按季结算的利息不少于按月结算的利息.
例5 用10 000 元购买某个理财产品一年.
(1)若以月利率0.400%的复利计息,12个月能获得多少利息(精确到1元)?
(2)若以季度复利计息,存4个季度,则当每季度利率为多少时,按季结算的利息不少于按月结算的利息(精确到)?
例题讲解
例6 某工厂去年12月试产1050个高新电子产品,产品合格率为90%. 从今年1月开始,工厂在接下来的两年中将生产这款产品. 1月按去年12月的产量和产品合格率生产,以后每月的产量都在前一个月的基础上提高5%,产品合格率比前一个月增加0.4%,那么生产该产品一年后,月不合格品的数量能否控制在100个以内?
例题讲解
解:设从今年1月起,各月的产量及不合格率分别构成数列,.
,
,其中,n=1,2,…,24,
则从今年1月起,各月不合格产品的数量是
由,得
所以,当时,递减,又
所以,当时,
所以,生产该产品一年后,月不合格品的数量能控制在100以内.
