人教B版(2019)高中数学必修第一册 1.2.2 全称量词命题与存在量词命题的否定 课件(共19张PPT)
文档属性
| 名称 | 人教B版(2019)高中数学必修第一册 1.2.2 全称量词命题与存在量词命题的否定 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 364.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
1.2 常用逻辑用语
第一章 集合与常用逻辑用语
1.2.2 全称量词命题与存在量词命题的否定
学习目标
1.能正确使用存在量词对全称量词命题进行否定,
2.能正确使用全称量词对存在量词命题进行否定.
学习目标
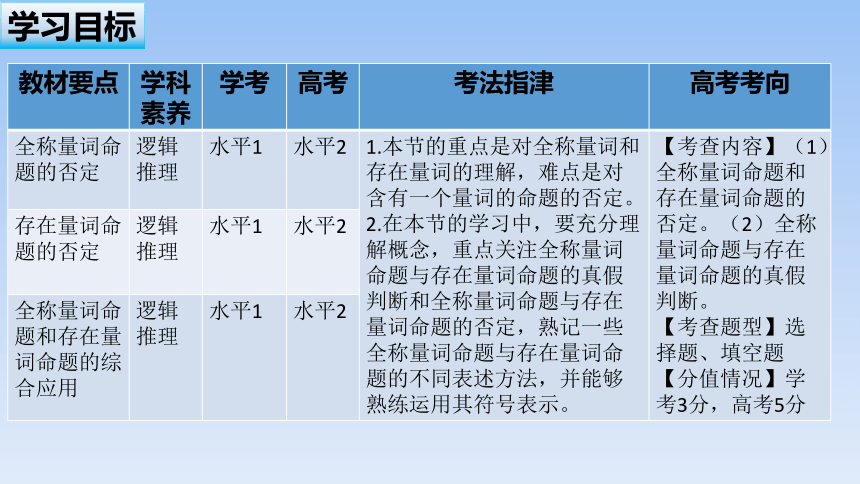
教材要点 学科素养 学考 高考 考法指津 高考考向
全称量词命题的否定 逻辑推理 水平1 水平2 1.本节的重点是对全称量词和存在量词的理解,难点是对含有一个量词的命题的否定。 2.在本节的学习中,要充分理解概念,重点关注全称量词命题与存在量词命题的真假判断和全称量词命题与存在量词命题的否定,熟记一些全称量词命题与存在量词命题的不同表述方法,并能够熟练运用其符号表示。 【考查内容】(1)全称量词命题和存在量词命题的否定。(2)全称量词命题与存在量词命题的真假判断。
【考查题型】选择题、填空题【分值情况】学考3分,高考5分
存在量词命题的否定 逻辑推理 水平1 水平2
全称量词命题和存在量词命题的综合应用 逻辑推理 水平1 水平2
知识点一 全称量词命题与存在量词命题的否定
(一)教材梳理填空
一、自学教材·注重基础
(1)存在量词命题的否定:对含有一个量词的存在量词命题的否定,有下面的结论:存在量词命题p: x∈M,p(x),它的否定綈p:________________.
存在量词命题的否定是全称量词命题.
(2)全称量词命题的否定:对含有一个量词的全称量词命题的否定,有下面的结论:全称量词命题p: x∈M,p(x),它的否定綈p:________________
全称量词命题的否定是存在量词命题.
(3)在书写这两种命题的否定时,相应地___________变为全称量词,全称量词变为 ___________ .
(二)基本知能小试
1.判断正误
(1)命题“ x∈{x|x≥0},x3+x≥0”的否定是“ x∈{x|x≥0},x3+x<0”. ( )
(2) x∈M,p(x)与 x∈M,綈p(x)的真假性相反. ( )
(3)从存在量词命题的否定看,是对“量词”和“p(x)”同时否定. ( )
√
×
一、自学教材·注重基础
知识点一 全称量词命题与存在量词命题的否定
√
(二)基本知能小试
2.若命题p: x>0,x2-3x+2>0,则命题p的否定为( )
A. x>0,x2-3x+2≤0 B. x≤0,x2-3x+2≤0
C. x>0,x2-3x+2≤0 D. x≤0,x2-3x+2≤0
解析:命题p是一个存在量词命题,綈p为: x>0,x2-3x+2≤0.
C
一、自学教材·注重基础
知识点一 全称量词命题与存在量词命题的否定
3.已知命题p: x>2,x3-8>0,那么p的否定是_________________.
解析:命题p为全称量词命题,其否定为存在量词命题,则綈p: x>2,x3-8≤0.
x>2,x3-8≤0
题型一 全称量词命题的否定
二、提升新知·注重综合
例1、写出下列全称量词命题的否定,并判断其否定的真假.
(1)对所有正数x,>x+1;
(2) x∈R,x3+1≠0;
(3)所有被5整除的整数都是奇数;
(3)所有的正方形都是矩形.
解析
(1)该命题的否定:存在正数x,≤x+1,真命题.
(2)该命题的否定: x∈R,x3+1=0,真命题.
(3)该命题的否定:存在一个被5整除的整数不是奇数,真命题.
(4)该命题的否定:至少存在一个正方形不是矩形
二、提升新知·注重综合
方法总结
题型一 全称量词命题的否定
1.对全称量词命题否定的两个步骤
(1)改变量词:把全称量词换为恰当的存在量词.
(2)否定结论:原命题中的“是”“成立”等改为“不是”“不成立”等.
2.全称量词命题否定后的真假判断方法
全称量词命题的否定是存在量词命题,其真假性与全称量词命题相反;要说明一个全称量词命题是假命题,只需举一个反例即可.
变式训练
写出下列全称量词命题的否定:
(1) x∈{-2,-1,0,1,2},|x-2|≥2.
(2)任何一个实数除以1,仍等于这个数.
(3)所有分数都是有理数.
(4)任意两个等边三角形都相似.
解析:(1)该命题的否定: x∈{-2,-1,0,1,2},|x-2|<2.
(2)该命题的否定:存在一个实数除以1,不等于这个数.
(3)该命题的否定:存在一个分数不是有理数.
(4)该命题的否定:存在两个等边三角形,它们不相似.
二、提升新知·注重综合
题型一 全称量词命题的否定
解析
二、提升新知·注重综合
例2、(1)命题p: x>0,x+=2,则綈p为 ( )
A. x>0,x+ =2 B. x>0,x+ ≠2
C. x≤0,x+ =2 D. x≤0,x+ ≠2
(1)存在量词命题的否定为全称量词命题:把 → ,x+ =2→x+ ≠2,故选B.
题型二 存在量词命题的否定
B
解析
二、提升新知·注重综合
(2)写出下列存在量词命题的否定,并判断其否定的真假.
①有些实数的绝对值是正数; ②某些平行四边形是菱形;
③ x∈R,x2+1<0; ④ x,y∈Z,使得x+y=3.
(2)①该命题的否定:“不存在一个实数,它的绝对值是正数”.也即“所有实数的绝对值都不是正数”.假命题.
②该命题的否定:“没有一个平行四边形是菱形”,也即“每一个平行四边形都不是菱形”.假命题.
③该命题的否定:“不存在x∈R,x2+1<0”,也即“ x∈R,x2+1≥0”.真命题.
④该命题的否定:“ x,y∈Z,x+y≠3”.假命题.
题型二 存在量词命题的否定
方法总结
二、提升新知·注重综合
题型二 存在量词命题的否定
1.对存在量词命题否定的两个步骤
(1)改变量词:把存在量词换为恰当的全称量词.
(2)否定结论:原命题中的“有”“存在”等更改为“没有”“不存在”等.
2.存在量词命题否定后的真假判断
存在量词命题的否定是全称量词命题,其真假性与存在量词命题相反;要说明一个存在量词命题是真命题,只需要找到一个实例即可.
变式训练
二、提升新知·注重综合
题型二 存在量词命题的否定
判断下列命题的真假,并写出这些命题的否定:
(1)某些梯形的对角线互相平分.
(2) x∈R,x3-1=0.
(3)在同圆中,同弧所对的圆周角相等.
(4)有些素数是奇数.
解析:(1)假命题.该命题的否定:任意一个梯形的对角线都不互相平分.
(2)真命题.该命题的否定: x∈R,x3-1≠0.
(3)真命题.该命题的否定:在同圆中,同弧所对的圆周角不相等.
(4)真命题.该命题的否定:所有的素数都不是奇数.
例3、(1)已知命题p: x∈(1,3),x-a≥0;若綈p是真命题,则实数a的取值范围是 ( )
A.(-∞,1) B.(3,+∞)
C.(-∞,3] D.[3,+∞)
(2)已知命题p:“ x∈R,mx2≥0”是真命题,则实数m的取值范围是___________.
题型三 全称量词命题与存在量词命题的应用
x∈(1,3),x-a≥0的否定为 x∈(1,3),x-a<0,
因为綈p为真命题,所以x故a≥3.
(2)因为 x∈R,x2≥0是真命题,
故若 x∈R,mx2≥0是真命题,则有m≥0.
解析
二、提升新知·注重综合
D
[0,+∞)
方法总结
二、提升新知·注重综合
题型三 全称量词命题与存在量词命题的应用
利用含量词的命题的真假求参数范围的技巧
(1)含参数的全称量词为真时,常与不等式恒成立有关,可根据有关代数恒等式(如x2≥0),确定参数的范围.
(2)含参数的存在量词命题为真时,常转化为方程或不等式有解问题来处理.
变式训练
1.已知命题: x≥3,2x-1≥m是真命题,则实数m的取值范围为________.
解析:因为x≥3,所以2x-1≥5,又因为 x≥3,2x-1≥m是真命题,所以m≤5.
(-∞,5]
{a∈R|a≠3}
2.已知命题p:“ x∈R,(a-3)x+1=0”是真命题,则实数a的取值集合是__________.
解析:因为“ x∈R,(a-3)x+1=0”是真命题,所以关于x的方程(a-3)x+1=0有实数解,所以a-3≠0,即a≠3,所以实数a的取值集合是{a∈R|a≠3}.
二、提升新知·注重综合
题型三 全称量词命题与存在量词命题的应用
当堂练习
1.命题“ x∈R,x2=x”的否定是 ( )
A. x∈R,x2≠x B. x∈R,x2=x
C. x R,x2≠x D. x∈R,x2≠x
一、基础经典题
D
2.命题p: x∈N,x3A. x∈N,x3≥x2 B. x∈N,x3C. x∈N,x3>x2 D. x∈N,x3≥x2
解析:命题p: x∈N,x3D
三、训练素养·注重应用、创新
当堂练习
3.已知命题p: x,y∈Z,x2+y2=2 019,则綈p为 ( )
A. x,y∈Z,x2+y2≠2 019
B. x,y∈Z,x2+y2≠2 019
C. x,y∈Z,x2+y2=2 019
D.不存在x,y∈Z,x2+y2=2 019
解析:由题意知, → ,x2+y2=2 019→x2+y2≠2 019.故选A.
A
三、训练素养·注重应用、创新
当堂练习
4.写出下列命题的否定.
(1)所有自然数的平方是正数;
(2)任何实数x都是方程5x-12=0的根;
(3)有些整数是奇数.
解析:(1)有些自然数的平方不是正数.
(2)存在实数x不是方程5x-12=0的根.
(3)所有的整数都不是奇数.
二、创新应用题
三、训练素养·注重应用、创新
1.2 常用逻辑用语
第一章 集合与常用逻辑用语
1.2.2 全称量词命题与存在量词命题的否定
学习目标
1.能正确使用存在量词对全称量词命题进行否定,
2.能正确使用全称量词对存在量词命题进行否定.
学习目标
教材要点 学科素养 学考 高考 考法指津 高考考向
全称量词命题的否定 逻辑推理 水平1 水平2 1.本节的重点是对全称量词和存在量词的理解,难点是对含有一个量词的命题的否定。 2.在本节的学习中,要充分理解概念,重点关注全称量词命题与存在量词命题的真假判断和全称量词命题与存在量词命题的否定,熟记一些全称量词命题与存在量词命题的不同表述方法,并能够熟练运用其符号表示。 【考查内容】(1)全称量词命题和存在量词命题的否定。(2)全称量词命题与存在量词命题的真假判断。
【考查题型】选择题、填空题【分值情况】学考3分,高考5分
存在量词命题的否定 逻辑推理 水平1 水平2
全称量词命题和存在量词命题的综合应用 逻辑推理 水平1 水平2
知识点一 全称量词命题与存在量词命题的否定
(一)教材梳理填空
一、自学教材·注重基础
(1)存在量词命题的否定:对含有一个量词的存在量词命题的否定,有下面的结论:存在量词命题p: x∈M,p(x),它的否定綈p:________________.
存在量词命题的否定是全称量词命题.
(2)全称量词命题的否定:对含有一个量词的全称量词命题的否定,有下面的结论:全称量词命题p: x∈M,p(x),它的否定綈p:________________
全称量词命题的否定是存在量词命题.
(3)在书写这两种命题的否定时,相应地___________变为全称量词,全称量词变为 ___________ .
(二)基本知能小试
1.判断正误
(1)命题“ x∈{x|x≥0},x3+x≥0”的否定是“ x∈{x|x≥0},x3+x<0”. ( )
(2) x∈M,p(x)与 x∈M,綈p(x)的真假性相反. ( )
(3)从存在量词命题的否定看,是对“量词”和“p(x)”同时否定. ( )
√
×
一、自学教材·注重基础
知识点一 全称量词命题与存在量词命题的否定
√
(二)基本知能小试
2.若命题p: x>0,x2-3x+2>0,则命题p的否定为( )
A. x>0,x2-3x+2≤0 B. x≤0,x2-3x+2≤0
C. x>0,x2-3x+2≤0 D. x≤0,x2-3x+2≤0
解析:命题p是一个存在量词命题,綈p为: x>0,x2-3x+2≤0.
C
一、自学教材·注重基础
知识点一 全称量词命题与存在量词命题的否定
3.已知命题p: x>2,x3-8>0,那么p的否定是_________________.
解析:命题p为全称量词命题,其否定为存在量词命题,则綈p: x>2,x3-8≤0.
x>2,x3-8≤0
题型一 全称量词命题的否定
二、提升新知·注重综合
例1、写出下列全称量词命题的否定,并判断其否定的真假.
(1)对所有正数x,>x+1;
(2) x∈R,x3+1≠0;
(3)所有被5整除的整数都是奇数;
(3)所有的正方形都是矩形.
解析
(1)该命题的否定:存在正数x,≤x+1,真命题.
(2)该命题的否定: x∈R,x3+1=0,真命题.
(3)该命题的否定:存在一个被5整除的整数不是奇数,真命题.
(4)该命题的否定:至少存在一个正方形不是矩形
二、提升新知·注重综合
方法总结
题型一 全称量词命题的否定
1.对全称量词命题否定的两个步骤
(1)改变量词:把全称量词换为恰当的存在量词.
(2)否定结论:原命题中的“是”“成立”等改为“不是”“不成立”等.
2.全称量词命题否定后的真假判断方法
全称量词命题的否定是存在量词命题,其真假性与全称量词命题相反;要说明一个全称量词命题是假命题,只需举一个反例即可.
变式训练
写出下列全称量词命题的否定:
(1) x∈{-2,-1,0,1,2},|x-2|≥2.
(2)任何一个实数除以1,仍等于这个数.
(3)所有分数都是有理数.
(4)任意两个等边三角形都相似.
解析:(1)该命题的否定: x∈{-2,-1,0,1,2},|x-2|<2.
(2)该命题的否定:存在一个实数除以1,不等于这个数.
(3)该命题的否定:存在一个分数不是有理数.
(4)该命题的否定:存在两个等边三角形,它们不相似.
二、提升新知·注重综合
题型一 全称量词命题的否定
解析
二、提升新知·注重综合
例2、(1)命题p: x>0,x+=2,则綈p为 ( )
A. x>0,x+ =2 B. x>0,x+ ≠2
C. x≤0,x+ =2 D. x≤0,x+ ≠2
(1)存在量词命题的否定为全称量词命题:把 → ,x+ =2→x+ ≠2,故选B.
题型二 存在量词命题的否定
B
解析
二、提升新知·注重综合
(2)写出下列存在量词命题的否定,并判断其否定的真假.
①有些实数的绝对值是正数; ②某些平行四边形是菱形;
③ x∈R,x2+1<0; ④ x,y∈Z,使得x+y=3.
(2)①该命题的否定:“不存在一个实数,它的绝对值是正数”.也即“所有实数的绝对值都不是正数”.假命题.
②该命题的否定:“没有一个平行四边形是菱形”,也即“每一个平行四边形都不是菱形”.假命题.
③该命题的否定:“不存在x∈R,x2+1<0”,也即“ x∈R,x2+1≥0”.真命题.
④该命题的否定:“ x,y∈Z,x+y≠3”.假命题.
题型二 存在量词命题的否定
方法总结
二、提升新知·注重综合
题型二 存在量词命题的否定
1.对存在量词命题否定的两个步骤
(1)改变量词:把存在量词换为恰当的全称量词.
(2)否定结论:原命题中的“有”“存在”等更改为“没有”“不存在”等.
2.存在量词命题否定后的真假判断
存在量词命题的否定是全称量词命题,其真假性与存在量词命题相反;要说明一个存在量词命题是真命题,只需要找到一个实例即可.
变式训练
二、提升新知·注重综合
题型二 存在量词命题的否定
判断下列命题的真假,并写出这些命题的否定:
(1)某些梯形的对角线互相平分.
(2) x∈R,x3-1=0.
(3)在同圆中,同弧所对的圆周角相等.
(4)有些素数是奇数.
解析:(1)假命题.该命题的否定:任意一个梯形的对角线都不互相平分.
(2)真命题.该命题的否定: x∈R,x3-1≠0.
(3)真命题.该命题的否定:在同圆中,同弧所对的圆周角不相等.
(4)真命题.该命题的否定:所有的素数都不是奇数.
例3、(1)已知命题p: x∈(1,3),x-a≥0;若綈p是真命题,则实数a的取值范围是 ( )
A.(-∞,1) B.(3,+∞)
C.(-∞,3] D.[3,+∞)
(2)已知命题p:“ x∈R,mx2≥0”是真命题,则实数m的取值范围是___________.
题型三 全称量词命题与存在量词命题的应用
x∈(1,3),x-a≥0的否定为 x∈(1,3),x-a<0,
因为綈p为真命题,所以x
(2)因为 x∈R,x2≥0是真命题,
故若 x∈R,mx2≥0是真命题,则有m≥0.
解析
二、提升新知·注重综合
D
[0,+∞)
方法总结
二、提升新知·注重综合
题型三 全称量词命题与存在量词命题的应用
利用含量词的命题的真假求参数范围的技巧
(1)含参数的全称量词为真时,常与不等式恒成立有关,可根据有关代数恒等式(如x2≥0),确定参数的范围.
(2)含参数的存在量词命题为真时,常转化为方程或不等式有解问题来处理.
变式训练
1.已知命题: x≥3,2x-1≥m是真命题,则实数m的取值范围为________.
解析:因为x≥3,所以2x-1≥5,又因为 x≥3,2x-1≥m是真命题,所以m≤5.
(-∞,5]
{a∈R|a≠3}
2.已知命题p:“ x∈R,(a-3)x+1=0”是真命题,则实数a的取值集合是__________.
解析:因为“ x∈R,(a-3)x+1=0”是真命题,所以关于x的方程(a-3)x+1=0有实数解,所以a-3≠0,即a≠3,所以实数a的取值集合是{a∈R|a≠3}.
二、提升新知·注重综合
题型三 全称量词命题与存在量词命题的应用
当堂练习
1.命题“ x∈R,x2=x”的否定是 ( )
A. x∈R,x2≠x B. x∈R,x2=x
C. x R,x2≠x D. x∈R,x2≠x
一、基础经典题
D
2.命题p: x∈N,x3
解析:命题p: x∈N,x3
三、训练素养·注重应用、创新
当堂练习
3.已知命题p: x,y∈Z,x2+y2=2 019,则綈p为 ( )
A. x,y∈Z,x2+y2≠2 019
B. x,y∈Z,x2+y2≠2 019
C. x,y∈Z,x2+y2=2 019
D.不存在x,y∈Z,x2+y2=2 019
解析:由题意知, → ,x2+y2=2 019→x2+y2≠2 019.故选A.
A
三、训练素养·注重应用、创新
当堂练习
4.写出下列命题的否定.
(1)所有自然数的平方是正数;
(2)任何实数x都是方程5x-12=0的根;
(3)有些整数是奇数.
解析:(1)有些自然数的平方不是正数.
(2)存在实数x不是方程5x-12=0的根.
(3)所有的整数都不是奇数.
二、创新应用题
三、训练素养·注重应用、创新
