人教B版(2019)高中数学必修第一册 1.2.2全称量词命题与存在量词命题的否定 教学设计(表格式)
文档属性
| 名称 | 人教B版(2019)高中数学必修第一册 1.2.2全称量词命题与存在量词命题的否定 教学设计(表格式) |
|
|
| 格式 | docx | ||
| 文件大小 | 78.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 00:00:00 | ||
图片预览

文档简介
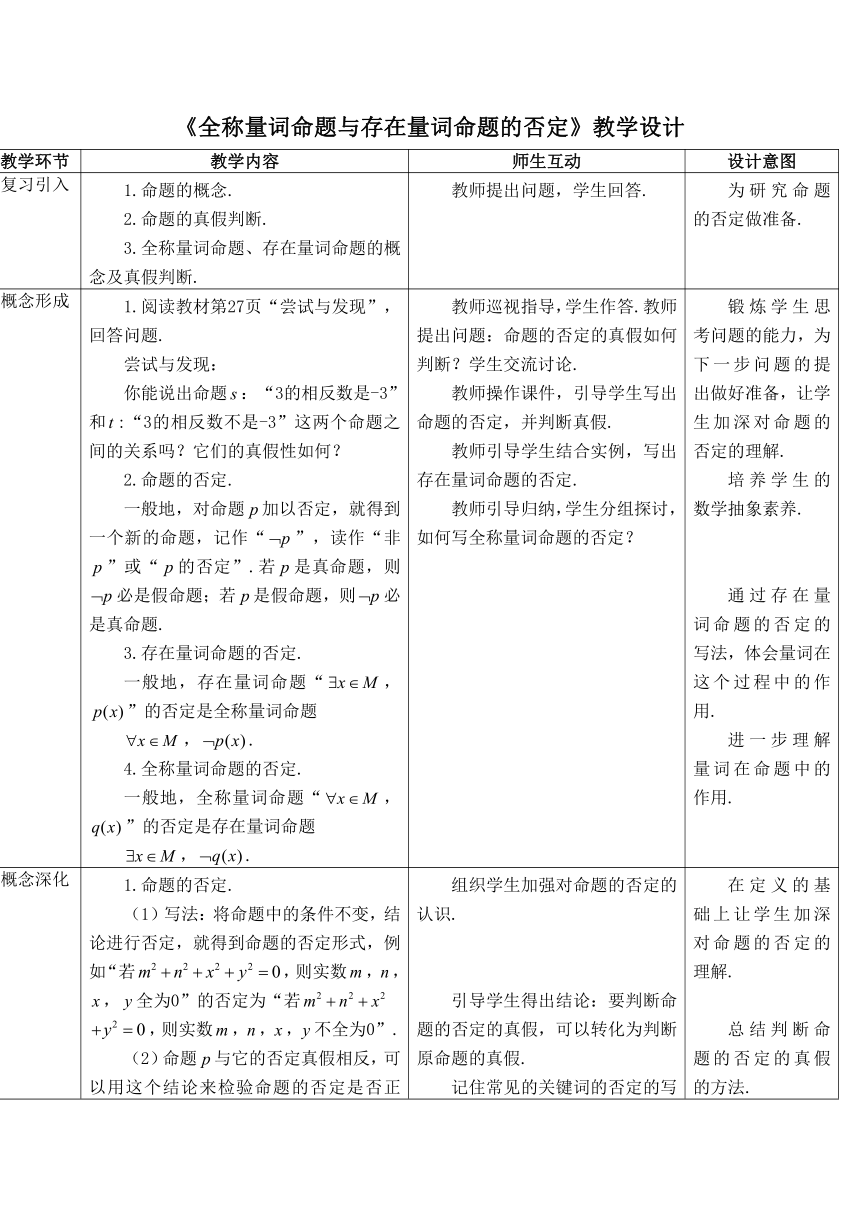
《全称量词命题与存在量词命题的否定》教学设计
教学环节 教学内容 师生互动 设计意图
复习引入 1.命题的概念. 2.命题的真假判断. 3.全称量词命题、存在量词命题的概念及真假判断. 教师提出问题,学生回答. 为研究命题的否定做准备.
概念形成 1.阅读教材第27页“尝试与发现”,回答问题. 尝试与发现: 你能说出命题:“3的相反数是-3”和:“3的相反数不是-3”这两个命题之间的关系吗?它们的真假性如何? 2.命题的否定. 一般地,对命题加以否定,就得到一个新的命题,记作“”,读作“非”或“的否定”.若是真命题,则必是假命题;若是假命题,则必是真命题. 3.存在量词命题的否定. 一般地,存在量词命题“,”的否定是全称量词命题 ,. 4.全称量词命题的否定. 一般地,全称量词命题“,”的否定是存在量词命题 ,. 教师巡视指导,学生作答.教师提出问题:命题的否定的真假如何判断?学生交流讨论. 教师操作课件,引导学生写出命题的否定,并判断真假. 教师引导学生结合实例,写出存在量词命题的否定. 教师引导归纳,学生分组探讨,如何写全称量词命题的否定? 锻炼学生思考问题的能力,为下一步问题的提出做好准备,让学生加深对命题的否定的理解. 培养学生的数学抽象素养. 通过存在量词命题的否定的写法,体会量词在这个过程中的作用. 进一步理解量词在命题中的作用.
概念深化 1.命题的否定. (1)写法:将命题中的条件不变,结论进行否定,就得到命题的否定形式,例如“若,则实数,, ,全为0”的否定为“若 ,则实数,,,不全为0”. (2)命题与它的否定真假相反,可以用这个结论来检验命题的否定是否正确. (3)常见关键词的否定形式如下表: 关键词否定词等于不等于能不能至少有一个一个都没有 都是不都是没有至少有一个
关键词否定词大于不大于小于不小于至多有一个至少有两个是不是属于不属于
2.全称量词命题与存在量词命题的否定. (1)含有一个量词的命题的否定,是在否定结论的同时改变量词的属性,即将全称量词改为存在量词,存在量词改为全称量词,所以全称量词命题的否定是存在量词命题,存在量词命题的否定是全称量词命题. (2)对含有一个量词的命题进行否定时,应根据命题的叙述对象的特征,挖掘其中的量词. 组织学生加强对命题的否定的认识. 引导学生得出结论:要判断命题的否定的真假,可以转化为判断原命题的真假. 记住常见的关键词的否定的写法,特别是“大于”的否定不是小于,而是“不大于”,即“小于等于”,“都是”的否定是“不都是”,而不是“都不是”. 教师引导学生紧扣定义求含有一个量词的命题的否定,学生可以进行小组讨论. 组织学生在小组内进行举例,评判,然后以小组为单位汇总后进行回答. 在定义的基础上让学生加深对命题的否定的理解. 总结判断命题的否定的真假的方法. 正确使用否定词. 在熟练掌握定义的基础上,激发学生的潜能,达到多思多说的目的,进一步让学生加深对本课时内容的理解.
应用举例 例1 教材第28~29页例1. 练习:教材第29页练习A第2,3题. 例2 教材第29页例2. 练习:教材第29页练习B第1题. 教师板书例1,引导学生自己解决问题,让学生板演. 学生分组练习,交流讨论,教师巡视,收集信息,及时评价. 学生自学例2,教师引导归纳. 学生练习,教师做好巡视指导. 锻炼学生的知识应用能力. 进一步加深对命题的否定的认识.
归纳小结 1.知识:(1)命题的否定的定义; (2)全称量词命题的否定; (3)存在量词命题的否定. 2.方法:命题的否定的写法、真假的判断方法. 学生相互交流收获与体会,并进行反思. 关注学生的自主体验.
布置作业 1.教材第29页练习A第1题. 2.教材第29页练习B第2题. 3.选做题:教材第29页练习B第3题. 学生独立完成前两题,教师批阅. 通过分层作业使学生巩固所学内容,并为有余力的学生提供进一步学习的机会.
板书设计
1.2.2 全称量词命题与存在量词命题的否定 一、复习 1.命题的概念 2.全称量词命题与存在量词命题及真假判断 二、新课 1.命题的否定 2.存在量词命题“,”的否定是,; 全称量词命题“,”的否定是,. 3.命题的否定的应用 三、例题 例1 例2 四、小结 1.知识 (1)命题的否定的定义; (2)存在量词命题的否定; (3)全称量词命题的否定 2.方法
教学研讨
教学过程中要和学生一起分析实例,概括出命题的否定的写法,并归纳出以下结论:
1.命题的否定与原命题的真假相反.
2.存在量词命题“,”的否定是,;全称量词命题“,”的否定是,.
即存在量词命题的否定是全称量词命题,全称量词命题的否定是存在量词命题.
3.当含有一个量词的命题是假命题时,一般利用它与其否定命题的真假相反,即利用其否定为真命题转化解决.
通过此总结,使学生能够比较全面地掌握命题的否定.
教学环节 教学内容 师生互动 设计意图
复习引入 1.命题的概念. 2.命题的真假判断. 3.全称量词命题、存在量词命题的概念及真假判断. 教师提出问题,学生回答. 为研究命题的否定做准备.
概念形成 1.阅读教材第27页“尝试与发现”,回答问题. 尝试与发现: 你能说出命题:“3的相反数是-3”和:“3的相反数不是-3”这两个命题之间的关系吗?它们的真假性如何? 2.命题的否定. 一般地,对命题加以否定,就得到一个新的命题,记作“”,读作“非”或“的否定”.若是真命题,则必是假命题;若是假命题,则必是真命题. 3.存在量词命题的否定. 一般地,存在量词命题“,”的否定是全称量词命题 ,. 4.全称量词命题的否定. 一般地,全称量词命题“,”的否定是存在量词命题 ,. 教师巡视指导,学生作答.教师提出问题:命题的否定的真假如何判断?学生交流讨论. 教师操作课件,引导学生写出命题的否定,并判断真假. 教师引导学生结合实例,写出存在量词命题的否定. 教师引导归纳,学生分组探讨,如何写全称量词命题的否定? 锻炼学生思考问题的能力,为下一步问题的提出做好准备,让学生加深对命题的否定的理解. 培养学生的数学抽象素养. 通过存在量词命题的否定的写法,体会量词在这个过程中的作用. 进一步理解量词在命题中的作用.
概念深化 1.命题的否定. (1)写法:将命题中的条件不变,结论进行否定,就得到命题的否定形式,例如“若,则实数,, ,全为0”的否定为“若 ,则实数,,,不全为0”. (2)命题与它的否定真假相反,可以用这个结论来检验命题的否定是否正确. (3)常见关键词的否定形式如下表: 关键词否定词等于不等于能不能至少有一个一个都没有 都是不都是没有至少有一个
关键词否定词大于不大于小于不小于至多有一个至少有两个是不是属于不属于
2.全称量词命题与存在量词命题的否定. (1)含有一个量词的命题的否定,是在否定结论的同时改变量词的属性,即将全称量词改为存在量词,存在量词改为全称量词,所以全称量词命题的否定是存在量词命题,存在量词命题的否定是全称量词命题. (2)对含有一个量词的命题进行否定时,应根据命题的叙述对象的特征,挖掘其中的量词. 组织学生加强对命题的否定的认识. 引导学生得出结论:要判断命题的否定的真假,可以转化为判断原命题的真假. 记住常见的关键词的否定的写法,特别是“大于”的否定不是小于,而是“不大于”,即“小于等于”,“都是”的否定是“不都是”,而不是“都不是”. 教师引导学生紧扣定义求含有一个量词的命题的否定,学生可以进行小组讨论. 组织学生在小组内进行举例,评判,然后以小组为单位汇总后进行回答. 在定义的基础上让学生加深对命题的否定的理解. 总结判断命题的否定的真假的方法. 正确使用否定词. 在熟练掌握定义的基础上,激发学生的潜能,达到多思多说的目的,进一步让学生加深对本课时内容的理解.
应用举例 例1 教材第28~29页例1. 练习:教材第29页练习A第2,3题. 例2 教材第29页例2. 练习:教材第29页练习B第1题. 教师板书例1,引导学生自己解决问题,让学生板演. 学生分组练习,交流讨论,教师巡视,收集信息,及时评价. 学生自学例2,教师引导归纳. 学生练习,教师做好巡视指导. 锻炼学生的知识应用能力. 进一步加深对命题的否定的认识.
归纳小结 1.知识:(1)命题的否定的定义; (2)全称量词命题的否定; (3)存在量词命题的否定. 2.方法:命题的否定的写法、真假的判断方法. 学生相互交流收获与体会,并进行反思. 关注学生的自主体验.
布置作业 1.教材第29页练习A第1题. 2.教材第29页练习B第2题. 3.选做题:教材第29页练习B第3题. 学生独立完成前两题,教师批阅. 通过分层作业使学生巩固所学内容,并为有余力的学生提供进一步学习的机会.
板书设计
1.2.2 全称量词命题与存在量词命题的否定 一、复习 1.命题的概念 2.全称量词命题与存在量词命题及真假判断 二、新课 1.命题的否定 2.存在量词命题“,”的否定是,; 全称量词命题“,”的否定是,. 3.命题的否定的应用 三、例题 例1 例2 四、小结 1.知识 (1)命题的否定的定义; (2)存在量词命题的否定; (3)全称量词命题的否定 2.方法
教学研讨
教学过程中要和学生一起分析实例,概括出命题的否定的写法,并归纳出以下结论:
1.命题的否定与原命题的真假相反.
2.存在量词命题“,”的否定是,;全称量词命题“,”的否定是,.
即存在量词命题的否定是全称量词命题,全称量词命题的否定是存在量词命题.
3.当含有一个量词的命题是假命题时,一般利用它与其否定命题的真假相反,即利用其否定为真命题转化解决.
通过此总结,使学生能够比较全面地掌握命题的否定.
