3.1.2函数的表示法第2课时课件-2022-2023学年高一上学期数学人教A版(2019)必修第一册(共21张PPT)
文档属性
| 名称 | 3.1.2函数的表示法第2课时课件-2022-2023学年高一上学期数学人教A版(2019)必修第一册(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 15:54:20 | ||
图片预览








文档简介
(共21张PPT)
导语
同学们,函数的图象在整个函数的学习中占据重要的地位,因为它能带领我们直观的感受变量的发生、发展过程,就好像是有了“两个黄鹂鸣翠柳,一行白鹭上青天”,就能在我们的脑海里呈现出一幅优美的图象一样直接.
第2课时 函数的表示法(2)
第三章 3.1.2 函数的表示法
学习目标
1.掌握利用图象的变换法作图.
2.会求函数的解析式.
函数图象的画法
一
问题 除了我们所熟悉的“列表、描点、连线”作图,还有哪些作图的方法?
提示 平移变换、对称变换、翻折变换.
知识梳理
1.函数图象的平移变换
(1)左加右减:函数y=f(x)的图象沿x轴方向向左(a>0)或向右(a<0)平移|a|个单位长度得到函数y=f(x+a)的图象.
(2)上加下减:函数y=f(x)的图象沿y轴方向向上(b>0)或向下(b<0)平移|b|个单位长度得到函数y=f(x)+b的图象.
2.函数图象的对称变换
3.函数图象的翻折变换
(1)左右移动加减的是自变量,且不带系数与符号,上下移动加减的是函数值.
(2)自变量的绝对值是左右翻折,函数值的绝对值是上下翻折.
(3)若f(a-x)=f(a+x),则函数f(x)的图象关于x=a对称.
注意点:
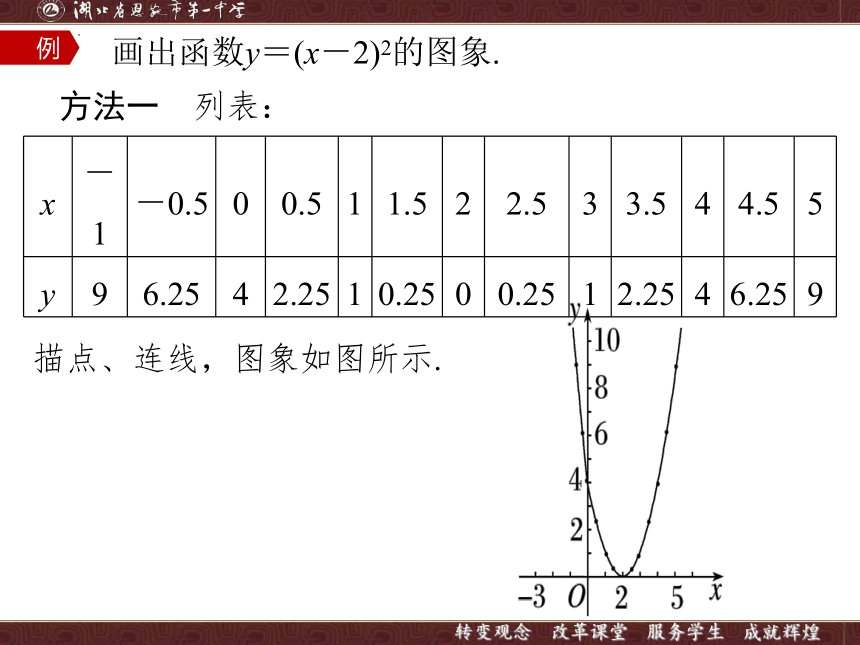
方法一 列表:
x -1 -0.5 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
y 9 6.25 4 2.25 1 0.25 0 0.25 1 2.25 4 6.25 9
描点、连线,图象如图所示.
画出函数y=(x-2)2的图象.
例1
方法二 图象变换法:先作出函数y=x2的图象,然后把它向右平移2个单位长度,就得到函数y=(x-2)2的图象,如图所示.
画函数图象的两种常见方法
(1)描点法:列表、描点、连线.
(2)变换作图法:常用的有水平平移变换、竖直平移变换、对称变换、翻折变换等.
反思感悟
跟踪训练1
√
求函数的解析式
二
则x=(t-1)2,t≥1,
所以f(t)=(t-1)2+2(t-1)=t2-1(t≥1),
所以f(x)的解析式为f(x)=x2-1(x≥1).
所以f(x)的解析式为f(x)=x2-1(x≥1).
例2
换元后范围保持一致
设f(x)=ax2+bx+c(a≠0),
则f(x+1)+f(x-1)
=a(x+1)2+b(x+1)+c+a(x-1)2+b(x-1)+c
=2ax2+2bx+2a+2c=2x2-4x,
(2)已知f(x)为二次函数,且f(x+1)+f(x-1)=2x2-4x,求f(x).
所以f(x)=x2-2x-1.
待定系数法
(3)已知2f(x)+ =x(x∈R且x≠0),求f(x)的解析式.
方程组法
求函数解析式的四种常用方法
(1)换元法:设t=g(x),解出x,代入f(g(x)),求f(t)的解析式即可.
(2)配凑法:对f(g(x))的解析式进行配凑变形,使它能用g(x)表示出来,再用x代替两边所有的“g(x)”即可.
(3)待定系数法:若已知f(x)的解析式的类型,设出它的一般形式,根据特殊值确定相关的系数即可.
(4)方程组法(或消元法):当同一个对应关系中的两个之间有互为相反数或互为倒数关系时,可构造方程组求解.
提醒:应用换元法求函数解析式时,务必保证函数在换元前后的等价性.
换元后范围保持一致
反思感悟
(1)已知f(x+1)=x2-3x+2,求f(x);
跟踪训练2
方法一 (配凑法):∵f(x+1)=x2-3x+2
=(x+1)2-5x+1=(x+1)2-5(x+1)+6,
∴f(x)=x2-5x+6.
方法二 (换元法):令t=x+1,则x=t-1,
∴f(t)=(t-1)2-3(t-1)+2=t2-5t+6,
即f(x)=x2-5x+6.
(2)已知函数f(x)是一次函数,若f(f(x))=4x+8,求f(x).
设f(x)=ax+b(a≠0),
则f(f(x))=f(ax+b)=a(ax+b)+b=a2x+ab+b.
又f(f(x))=4x+8,∴a2x+ab+b=4x+8,
(3)已知f(x)+2f(-x)=9x+2,求f(x)的解析式.
因为f(x)+2f(-x)=9x+2,
所以f(-x)+2f(x)=9(-x)+2,
②×2-①得3f(x)=-27x+2,
①
②
课堂小结
1.知识清单:
(1)函数的图象.
(2)求函数解析式.
2.方法归纳:待定系数法、换元法、配凑法、数形结合法.
3.常见误区:求函数解析式时容易忽视定义域.
导语
同学们,函数的图象在整个函数的学习中占据重要的地位,因为它能带领我们直观的感受变量的发生、发展过程,就好像是有了“两个黄鹂鸣翠柳,一行白鹭上青天”,就能在我们的脑海里呈现出一幅优美的图象一样直接.
第2课时 函数的表示法(2)
第三章 3.1.2 函数的表示法
学习目标
1.掌握利用图象的变换法作图.
2.会求函数的解析式.
函数图象的画法
一
问题 除了我们所熟悉的“列表、描点、连线”作图,还有哪些作图的方法?
提示 平移变换、对称变换、翻折变换.
知识梳理
1.函数图象的平移变换
(1)左加右减:函数y=f(x)的图象沿x轴方向向左(a>0)或向右(a<0)平移|a|个单位长度得到函数y=f(x+a)的图象.
(2)上加下减:函数y=f(x)的图象沿y轴方向向上(b>0)或向下(b<0)平移|b|个单位长度得到函数y=f(x)+b的图象.
2.函数图象的对称变换
3.函数图象的翻折变换
(1)左右移动加减的是自变量,且不带系数与符号,上下移动加减的是函数值.
(2)自变量的绝对值是左右翻折,函数值的绝对值是上下翻折.
(3)若f(a-x)=f(a+x),则函数f(x)的图象关于x=a对称.
注意点:
方法一 列表:
x -1 -0.5 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
y 9 6.25 4 2.25 1 0.25 0 0.25 1 2.25 4 6.25 9
描点、连线,图象如图所示.
画出函数y=(x-2)2的图象.
例1
方法二 图象变换法:先作出函数y=x2的图象,然后把它向右平移2个单位长度,就得到函数y=(x-2)2的图象,如图所示.
画函数图象的两种常见方法
(1)描点法:列表、描点、连线.
(2)变换作图法:常用的有水平平移变换、竖直平移变换、对称变换、翻折变换等.
反思感悟
跟踪训练1
√
求函数的解析式
二
则x=(t-1)2,t≥1,
所以f(t)=(t-1)2+2(t-1)=t2-1(t≥1),
所以f(x)的解析式为f(x)=x2-1(x≥1).
所以f(x)的解析式为f(x)=x2-1(x≥1).
例2
换元后范围保持一致
设f(x)=ax2+bx+c(a≠0),
则f(x+1)+f(x-1)
=a(x+1)2+b(x+1)+c+a(x-1)2+b(x-1)+c
=2ax2+2bx+2a+2c=2x2-4x,
(2)已知f(x)为二次函数,且f(x+1)+f(x-1)=2x2-4x,求f(x).
所以f(x)=x2-2x-1.
待定系数法
(3)已知2f(x)+ =x(x∈R且x≠0),求f(x)的解析式.
方程组法
求函数解析式的四种常用方法
(1)换元法:设t=g(x),解出x,代入f(g(x)),求f(t)的解析式即可.
(2)配凑法:对f(g(x))的解析式进行配凑变形,使它能用g(x)表示出来,再用x代替两边所有的“g(x)”即可.
(3)待定系数法:若已知f(x)的解析式的类型,设出它的一般形式,根据特殊值确定相关的系数即可.
(4)方程组法(或消元法):当同一个对应关系中的两个之间有互为相反数或互为倒数关系时,可构造方程组求解.
提醒:应用换元法求函数解析式时,务必保证函数在换元前后的等价性.
换元后范围保持一致
反思感悟
(1)已知f(x+1)=x2-3x+2,求f(x);
跟踪训练2
方法一 (配凑法):∵f(x+1)=x2-3x+2
=(x+1)2-5x+1=(x+1)2-5(x+1)+6,
∴f(x)=x2-5x+6.
方法二 (换元法):令t=x+1,则x=t-1,
∴f(t)=(t-1)2-3(t-1)+2=t2-5t+6,
即f(x)=x2-5x+6.
(2)已知函数f(x)是一次函数,若f(f(x))=4x+8,求f(x).
设f(x)=ax+b(a≠0),
则f(f(x))=f(ax+b)=a(ax+b)+b=a2x+ab+b.
又f(f(x))=4x+8,∴a2x+ab+b=4x+8,
(3)已知f(x)+2f(-x)=9x+2,求f(x)的解析式.
因为f(x)+2f(-x)=9x+2,
所以f(-x)+2f(x)=9(-x)+2,
②×2-①得3f(x)=-27x+2,
①
②
课堂小结
1.知识清单:
(1)函数的图象.
(2)求函数解析式.
2.方法归纳:待定系数法、换元法、配凑法、数形结合法.
3.常见误区:求函数解析式时容易忽视定义域.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
