人教B版(2019)高中数学必修第一册 【 整合精品课件】1.2.3《充分条件、必要条件》(共31张PPT)
文档属性
| 名称 | 人教B版(2019)高中数学必修第一册 【 整合精品课件】1.2.3《充分条件、必要条件》(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 881.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 15:52:06 | ||
图片预览











文档简介
(共31张PPT)
1.2 常用逻辑用语
第一章 集合与常用逻辑用语
1.2.3 充分条件、必要条件
1.通过对典型数学命题的梳理,理解必要条件的意义,理解性质定理与必要条件的关系,
2.通过对典型数学命题的梳理,理解充分条件的意义,理解判定定理与充分条件的关系,
3.通过对典型数学命题的梳理,理解充要条件的意义,理解数学定义与充要条件的关系.
学习目标
学习目标
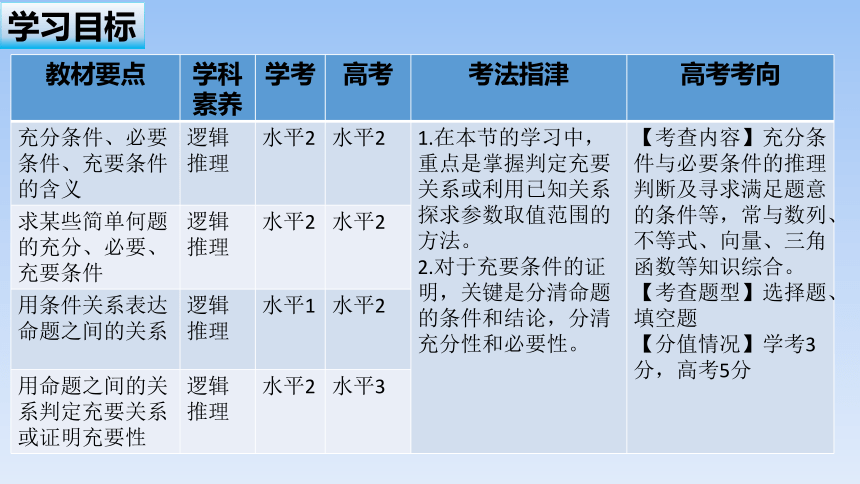
教材要点 学科素养 学考 高考 考法指津 高考考向
充分条件、必要条件、充要条件的含义 逻辑推理 水平2 水平2 1.在本节的学习中,重点是掌握判定充要关系或利用已知关系探求参数取值范围的方法。 2.对于充要条件的证明,关键是分清命题的条件和结论,分清充分性和必要性。 【考查内容】充分条件与必要条件的推理判断及寻求满足题意的条件等,常与数列、不等式、向量、三角函数等知识综合。【考查题型】选择题、填空题
【分值情况】学考3分,高考5分
求某些简单何题的充分、必要、充要条件 逻辑推理 水平2 水平2
用条件关系表达命题之间的关系 逻辑推理 水平1 水平2
用命题之间的关系判定充要关系或证明充要性 逻辑推理 水平2 水平3
知识点一 充分条件、必要条件
(一)教材梳理填空
一、自学教材·注重基础
(1)若“如果p,那么q”是一个真命题,则称由p可以推出q,记作________ ,读作________ ;否则,称由p推不出q,记作_______,读作____________ .
(2)当p q时,我们称p是q的________条件,q是p的________条件.
(3)当时,我们称p不是q的________条件,q不是p的________条件.
(二)基本知能小试
1.判断正误
(1)“两角不相等”是“两角不是对顶角”的必要条件. ( )
(2)若p是q的充分条件,则p是唯一的. ( )
(3)“x>0”是“x>1”的充分条件. ( )
(4)q不是p的必要条件时,“”成立. ( )
√
×
一、自学教材·注重基础
×
×
知识点一 充分条件、必要条件
(二)基本知能小试
一、自学教材·注重基础
知识点一 充分条件、必要条件
2.“x<0或x>4”的一个必要条件是 ( )
A.x<0 B.x>4
C.x<0或x>2 D.x<-1或x>5
解析:当x<0或x>4时,一定有x<0或x>2.
C
3.设集合M={x|0<x≤3},N={x|0必要
(二)基本知能小试
一、自学教材·注重基础
知识点一 充分条件、必要条件
4.若集合A={1,m2},B={2,4},则“m=2”是“A∩B={4}”的________条件.(填“充分”“必要”)
解析:当m=2时,m2=4,所以A∩B={4},所以“m=2”是“A∩B={4}”的充分条件.
充分
知识点二 充要条件
(一)教材梳理填空
一、自学教材·注重基础
(1)一般地,如果p q且qp,则称p是q的充分________条件.
(2)如果pq且q p,则称p是q的_____________条件.
(3)如果p q且q p,则称p是q的__________条件(简称为 _________ 条件),记作 ________,此时,也读作“p与q等价”“p当且仅当q”.
(二)基本知能小试
1.判断正误
(1)q是p的必要条件时,p是q的充分条件. ( )
(2)若p是q的充要条件,则命题p和q是两个相互等价的命题. ( )
一、自学教材·注重基础
√
√
2.“x<2”是“<0”的 ( )
A.充要条件 B.必要不充分条件
C.充分不必要条件 D.既不充分也不必要条件
A
知识点二 充要条件
解析:由<0得x-2<0得x<2,
即“x<2”是“<0”的充要条件,故选A.
(二)基本知能小试
一、自学教材·注重基础
知识点二 充要条件
3.设p:一元二次方程ax2+bx+c=0有实数根,q:b2-4ac≥0,则p是q的________条件.
解析:因为p q,q r,所以p r,所以p是r的充要条件.
充要
充要
4.若p是q的充要条件,q是r的充要条件,则p是r的________条件.
题型一 充分条件与必要条件的判定
(1)对“推出”的正确理解
对于命题p:∠A=30°,q:sin A=.显然p可以推出q,记为p q,而q是不能推出p的.
(2)若p q,则p是q的充分条件.所谓充分,就是说条件是充分的,也就是说条件是充足的,条件是足够的,条件是足以保证的.“有之必成立,无之未必不成立”.
(3)若p q,则q是p的必要条件.所谓必要,就是条件是必须有的,必不可少的,缺其不可.“有之未必成立,无之必不成立”.
二、提升新知·注重综合
例1、(1)“两个三角形面积相等”是“两个三角形全等”的___________条件.(填“充分”“必要”)
(2)判断下列说法中,p不是q的充分条件的是________.
①p:“x=1”,q:“x2-2x+1=0”;
②设a,b是实数,p:“a+b>0”,q:“ab>0”;
③p:四边形的对角线相等,q:四边形是平行四边形.
(1)设p:两个三角形面积相等;q:两个三角形全等,则pq,q p.
∴p是q的必要条件.
(2)对①,当x=1时,显然有x2-2x+1=0,故p q,即p是q的充分条件;
对②,当a=5,b=-1时,有a+b>0,但ab<0,故pq, p不是q的充分条件;
③∵四边形的对角线相等四边形是平行四边形,∴p不是q的充分条件.
解析
二、提升新知·注重综合
题型一 充分条件与必要条件的判定
必要
②③
二、提升新知·注重综合
方法总结
充分条件、必要条件的判断方法
定义法:①分清条件p和结论q:分清哪个是条件,哪个是结论;②找推式:判断“p q”及“q p”的真假;③下结论:根据定义下结论
等价法:将命题转化为另一个与之等价的、又便于判断真假的命题
集合法:写出集合A={x|p(x)}及B={x|q(x)},利用集合之间的包含关系加以判断.用集合法判断时,要尽可能用Venn图、数轴、直角坐标平面等几何方法,图形形象、直观,能简化解题过程,降低思维难度.
题型一 充分条件与必要条件的判定
变式训练
1.从“充分条件”“必要条件”中选出适当的一种填空:
(1)“ax2+bx+c=0(a≠0)有实根”是“ac<0”的__________.
(2)“△ABC≌△A′B′C′”是“△ABC∽△A′B′C′”的__________.
二、提升新知·注重综合
题型一 充分条件与必要条件的判定
必要条件
充分条件
2.设A,B是两个集合,判断“A∩B=A”是“A B”的什么条件.
解析:由题意得,A∩B=A A B,反之,A B A∩B=A,故“A∩B=A”是 “A B”的充分条件,也是必要条件.
变式训练
3.指出下列命题中,p是q的什么条件?
(1)p:x2=2x+1,q:x=;
(2)p:a2+b2=0,q:a+b=0;
(3)p:(x-1)2+(y-2)2=0,q:(x-1)(y-2)=0.
二、提升新知·注重综合
题型一 充分条件与必要条件的判定
解析:(1)∵x2=2x+1 x= ,x= x2=2x+1,
∴p是q的必要条件.
(2)∵a2+b2=0 a=b=0 a+b=0,a+b=0 / a2+b2=0,
∴p是q的充分条件.
(3)∵(x-1)2+(y-2)2=0 x=1且y=2 (x-1)·(y-2)=0,
而(x-1)(y-2)=0 / (x-1)2+(y-2)2=0,∴p是q的充分条件.
题型二 充要条件的判断
二、提升新知·注重综合
p是q的充要条件还有以下相同意义的说法:①当且仅当p成立时,q成立;②要使q成立,必须且只需p成立.
对充要条件的词义表达要熟悉.如“当且仅当”“必须且只需”“等价于”“反之亦成立”等.
二、提升新知·注重综合
(1)方程x2+x+m=0无实根 Δ=1-4m<0 m>.故选B.
(2)a2+b2>0,则a,b不同时为零;a,b中至少有一个不为零,则a2+b2>0.
例2、(1)“m>”是“一元二次方程x2+x+m=0无实数解”的 ( )
A.充分不必要条件 B.充要条件
C.必要不充分条件 D.既不充分也不必要条件
(2)a,b中至少有一个不为零的充要条件是( )
A.ab=0 B.ab>0 C.a2+b2=0 D.a2+b2>0
解析
题型二 充要条件的判断
B
D
二、提升新知·注重综合
方法总结
(1)如果p是q的充要条件,那么q也是p的充要条件,也就是说,如果p q,那么p与q互为充要条件.
(2)条件关系判定的常用结论:
题型二 充要条件的判断
条件p与结论q的关系 结论
p是q的充分不必要条件
p是q的必要不充分条件
p q,且q p,即p q p是q的充要条件
p是q的既不充分也不必要条件
变式训练
1.(2019·天津高考)设x∈R,则“0A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
B
解析:由“|x-1|<1”可得“0二、提升新知·注重综合
题型二 充要条件的判断
2.已知a,b是实数,则“a>0且b>0”是“a+b>0且ab>0”的________条件.
解析:a>0且b>0 a+b>0且ab>0,a+b>0且ab>0 a>0且b>0,故填充要.
充要
3.下列各题中,哪些p是q的充要条件?
(1)p:x=1;q:x-1= ;
(2)p:-1≤x≤5;q:x≥-1且x≤5;
(3)p:三角形是等边三角形;q:三角形是等腰三角形;
(4)p:A∩B=A,q: UB UA.
解析: (1)当x=1时,x-1= 成立;
当x-1= 时,x=1或x=2.
∴p不是q的充要条件,p是q的充分不必要条件.
(2)∵-1≤x≤5 x≥-1且x≤5,
∴p是q的充要条件.
二、提升新知·注重综合
变式训练
题型二 充要条件的判断
3.下列各题中,哪些p是q的充要条件?
(1)p:x=1;q:x-1= ;
(2)p:-1≤x≤5;q:x≥-1且x≤5;
(3)p:三角形是等边三角形;q:三角形是等腰三角形;
(4)p:A∩B=A,q: UB UA.
解析:(3)∵等边三角形一定是等腰三角形,而等腰三角形不一定都是等边三角形,
∴p不是q的充要条件,p是q的充分不必要条件.
(4)∵A∩B=A A B UB UA,
∴p是q的充要条件.
二、提升新知·注重综合
变式训练
题型二 充要条件的判断
例3、已知a+b≠0,证明a2+b2-a-b+2ab=0成立的充要条件是a+b=1.
题型三 充要条件的证明
先证充分性:
若a+b=1,
则a2+b2-a-b+2ab=(a+b)2-(a+b)=1-1=0,即充分性成立.
再证必要性:若a2+b2-a-b+2ab=0,
则(a+b)2-(a+b)=(a+b)·(a+b-1)=0.
∵a+b≠0,∴a+b-1=0,
即a+b=1成立,
综上,a2+b2-a-b+2ab=0成立的充要条件是a+b=1.
解析
二、提升新知·注重综合
二、提升新知·注重综合
方法总结
(1)先寻找必要条件,即将探求充要条件的对象视为结论,寻找使之成立的条件;再证明此条件是该对象的充分条件,即从充分性和必要性两方面说明.
(2)将原命题进行等价变形或转换,直至获得其成立的充要条件,探求的过程同时也是证明的过程,因为探求过程每一步都是等价的,所以不需要将充分性和必要性分开来证.
探求充要条件一般有两种方法
题型三 充要条件的证明
已知x,y都是非零实数,且x>y,求证:的充要条件是xy>0.
证明:(1)必要性:由,得,即,
又由x>y,得y-x<0,所以xy>0.
(2)充分性:由xy>0及x>y,得,即.
综上所述, 的充要条件是xy>0.
二、提升新知·注重综合
变式训练
题型三 充要条件的证明
例4、 已知p:-2≤x≤10,q:1-m≤x≤1+m(m>0),若p是q的必要不充分条件,求实数m的取值范围.
解析:p:-2≤x≤10,q:1-m≤x≤1+m(m>0).
因为p是q的必要不充分条件,
所以q是p的充分不必要条件,
即{x|1-m≤x≤1+m} {x|-2≤x≤10},
故有或
解得m≤3.
又m>0,所以实数m的取值范围为(0,3].
二、提升新知·注重综合
题型四 充分条件与必要条件应用
二、提升新知·注重综合
方法总结
(1)应用:可利用充分性与必要性进行相关问题的求解,特别是求参数的值或取值范围问题.
(2)求解步骤:先把p,q等价转化,利用充分条件、必要条件与集合间的包含关系,建立关于参数的不等式(组)进行求解.
(3)关键点:利用充分条件、必要条件求参数的取值范围的关键就是找出集合间的包含关系,要注意范围的临界值.
充分条件与必要条件的应用技巧
题型四 充分条件与必要条件应用
二、提升新知·注重综合
变式训练
题型四 充分条件与必要条件应用
例4、 已知p:-2≤x≤10,q:1-m≤x≤1+m(m>0),若p是q的必要不充分条件,求实数m的取值范围.
1.[变条件]若本例中“p是q的必要不充分条件”改为“p是q的充分不必要条件”,其他条件不变,求实数m的取值范围.
解析:p:-2≤x≤10,q:1-m≤x≤1+m(m>0).
因为p是q的充分不必要条件,
设p代表的集合为A,q代表的集合为B,所以AB.
所以或解得m≥9,
即实数m的取值范围是[9,+∞).
二、提升新知·注重综合
变式训练
题型四 充分条件与必要条件应用
例4、 已知p:-2≤x≤10,q:1-m≤x≤1+m(m>0),若p是q的必要不充分条件,求实数m的取值范围.
2.[变问法]本例中p,q不变,是否存在实数m使p是q的充要条件?若存在,求出m的值;若不存在,说明理由.
解析:因为p:-2≤x≤10,q:1-m≤x≤1+m(m>0).
若p是q的充要条件,则方程组无解.
故不存在实数m,使得p是q的充要条件.
当堂练习
1.设x∈R,则“1A.必要不充分条件 B.充分不必要条件
C.充要条件 D.既不充分也不必要条件
一、基础经典题
解析:“1∴“1B
三、训练素养·注重应用、创新
2.“x=1是x2-4x+3=0”的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
A
解析:若x=1,则x2-4x+3=0,是充分条件,若x2-4x+3=0,则x=1或x=3,不是必要条件.故选A.
当堂练习
3.下面四个条件中,使a>b成立的充分不必要条件是 ( )
A.a≥b+1 B.a>b-1
C.a2>b2 D.a3>b3
解析:由a≥b+1>b,从而a≥b+1 a>b;反之,如a=4,b=3.5,则4>3.5 3.5+1,故a>b a≥b+1,故A正确.
A
三、训练素养·注重应用、创新
4.王大妈在地摊上因为贪图便宜买了劣质商品,非常气愤地说了句“真是便宜没好货”,按照王大妈的理解,“好货”是“不便宜”的________________条件.
解析:“好货不便宜”是“便宜没好货”的逆否命题,
根据互为逆否命题的真假一致得到:“好货不便宜”是真命题.
所以“好货” “不便宜”,
所以“好货”是“不便宜”的充分不必要条件.
充分不必要
当堂练习
5.条件p:1-x<0,条件q:x>a,若p是q的充分不必要条件,求a的取值范围.
解析:p:x>1,若p是q的充分不必要条件,则p q,但qp,也就是说,p对应集合是q对应集合的真子集,所以a<1,即a的取值范围为(-∞,1).
二、创新应用题
三、训练素养·注重应用、创新
1.2 常用逻辑用语
第一章 集合与常用逻辑用语
1.2.3 充分条件、必要条件
1.通过对典型数学命题的梳理,理解必要条件的意义,理解性质定理与必要条件的关系,
2.通过对典型数学命题的梳理,理解充分条件的意义,理解判定定理与充分条件的关系,
3.通过对典型数学命题的梳理,理解充要条件的意义,理解数学定义与充要条件的关系.
学习目标
学习目标
教材要点 学科素养 学考 高考 考法指津 高考考向
充分条件、必要条件、充要条件的含义 逻辑推理 水平2 水平2 1.在本节的学习中,重点是掌握判定充要关系或利用已知关系探求参数取值范围的方法。 2.对于充要条件的证明,关键是分清命题的条件和结论,分清充分性和必要性。 【考查内容】充分条件与必要条件的推理判断及寻求满足题意的条件等,常与数列、不等式、向量、三角函数等知识综合。【考查题型】选择题、填空题
【分值情况】学考3分,高考5分
求某些简单何题的充分、必要、充要条件 逻辑推理 水平2 水平2
用条件关系表达命题之间的关系 逻辑推理 水平1 水平2
用命题之间的关系判定充要关系或证明充要性 逻辑推理 水平2 水平3
知识点一 充分条件、必要条件
(一)教材梳理填空
一、自学教材·注重基础
(1)若“如果p,那么q”是一个真命题,则称由p可以推出q,记作________ ,读作________ ;否则,称由p推不出q,记作_______,读作____________ .
(2)当p q时,我们称p是q的________条件,q是p的________条件.
(3)当时,我们称p不是q的________条件,q不是p的________条件.
(二)基本知能小试
1.判断正误
(1)“两角不相等”是“两角不是对顶角”的必要条件. ( )
(2)若p是q的充分条件,则p是唯一的. ( )
(3)“x>0”是“x>1”的充分条件. ( )
(4)q不是p的必要条件时,“”成立. ( )
√
×
一、自学教材·注重基础
×
×
知识点一 充分条件、必要条件
(二)基本知能小试
一、自学教材·注重基础
知识点一 充分条件、必要条件
2.“x<0或x>4”的一个必要条件是 ( )
A.x<0 B.x>4
C.x<0或x>2 D.x<-1或x>5
解析:当x<0或x>4时,一定有x<0或x>2.
C
3.设集合M={x|0<x≤3},N={x|0
(二)基本知能小试
一、自学教材·注重基础
知识点一 充分条件、必要条件
4.若集合A={1,m2},B={2,4},则“m=2”是“A∩B={4}”的________条件.(填“充分”“必要”)
解析:当m=2时,m2=4,所以A∩B={4},所以“m=2”是“A∩B={4}”的充分条件.
充分
知识点二 充要条件
(一)教材梳理填空
一、自学教材·注重基础
(1)一般地,如果p q且qp,则称p是q的充分________条件.
(2)如果pq且q p,则称p是q的_____________条件.
(3)如果p q且q p,则称p是q的__________条件(简称为 _________ 条件),记作 ________,此时,也读作“p与q等价”“p当且仅当q”.
(二)基本知能小试
1.判断正误
(1)q是p的必要条件时,p是q的充分条件. ( )
(2)若p是q的充要条件,则命题p和q是两个相互等价的命题. ( )
一、自学教材·注重基础
√
√
2.“x<2”是“<0”的 ( )
A.充要条件 B.必要不充分条件
C.充分不必要条件 D.既不充分也不必要条件
A
知识点二 充要条件
解析:由<0得x-2<0得x<2,
即“x<2”是“<0”的充要条件,故选A.
(二)基本知能小试
一、自学教材·注重基础
知识点二 充要条件
3.设p:一元二次方程ax2+bx+c=0有实数根,q:b2-4ac≥0,则p是q的________条件.
解析:因为p q,q r,所以p r,所以p是r的充要条件.
充要
充要
4.若p是q的充要条件,q是r的充要条件,则p是r的________条件.
题型一 充分条件与必要条件的判定
(1)对“推出”的正确理解
对于命题p:∠A=30°,q:sin A=.显然p可以推出q,记为p q,而q是不能推出p的.
(2)若p q,则p是q的充分条件.所谓充分,就是说条件是充分的,也就是说条件是充足的,条件是足够的,条件是足以保证的.“有之必成立,无之未必不成立”.
(3)若p q,则q是p的必要条件.所谓必要,就是条件是必须有的,必不可少的,缺其不可.“有之未必成立,无之必不成立”.
二、提升新知·注重综合
例1、(1)“两个三角形面积相等”是“两个三角形全等”的___________条件.(填“充分”“必要”)
(2)判断下列说法中,p不是q的充分条件的是________.
①p:“x=1”,q:“x2-2x+1=0”;
②设a,b是实数,p:“a+b>0”,q:“ab>0”;
③p:四边形的对角线相等,q:四边形是平行四边形.
(1)设p:两个三角形面积相等;q:两个三角形全等,则pq,q p.
∴p是q的必要条件.
(2)对①,当x=1时,显然有x2-2x+1=0,故p q,即p是q的充分条件;
对②,当a=5,b=-1时,有a+b>0,但ab<0,故pq, p不是q的充分条件;
③∵四边形的对角线相等四边形是平行四边形,∴p不是q的充分条件.
解析
二、提升新知·注重综合
题型一 充分条件与必要条件的判定
必要
②③
二、提升新知·注重综合
方法总结
充分条件、必要条件的判断方法
定义法:①分清条件p和结论q:分清哪个是条件,哪个是结论;②找推式:判断“p q”及“q p”的真假;③下结论:根据定义下结论
等价法:将命题转化为另一个与之等价的、又便于判断真假的命题
集合法:写出集合A={x|p(x)}及B={x|q(x)},利用集合之间的包含关系加以判断.用集合法判断时,要尽可能用Venn图、数轴、直角坐标平面等几何方法,图形形象、直观,能简化解题过程,降低思维难度.
题型一 充分条件与必要条件的判定
变式训练
1.从“充分条件”“必要条件”中选出适当的一种填空:
(1)“ax2+bx+c=0(a≠0)有实根”是“ac<0”的__________.
(2)“△ABC≌△A′B′C′”是“△ABC∽△A′B′C′”的__________.
二、提升新知·注重综合
题型一 充分条件与必要条件的判定
必要条件
充分条件
2.设A,B是两个集合,判断“A∩B=A”是“A B”的什么条件.
解析:由题意得,A∩B=A A B,反之,A B A∩B=A,故“A∩B=A”是 “A B”的充分条件,也是必要条件.
变式训练
3.指出下列命题中,p是q的什么条件?
(1)p:x2=2x+1,q:x=;
(2)p:a2+b2=0,q:a+b=0;
(3)p:(x-1)2+(y-2)2=0,q:(x-1)(y-2)=0.
二、提升新知·注重综合
题型一 充分条件与必要条件的判定
解析:(1)∵x2=2x+1 x= ,x= x2=2x+1,
∴p是q的必要条件.
(2)∵a2+b2=0 a=b=0 a+b=0,a+b=0 / a2+b2=0,
∴p是q的充分条件.
(3)∵(x-1)2+(y-2)2=0 x=1且y=2 (x-1)·(y-2)=0,
而(x-1)(y-2)=0 / (x-1)2+(y-2)2=0,∴p是q的充分条件.
题型二 充要条件的判断
二、提升新知·注重综合
p是q的充要条件还有以下相同意义的说法:①当且仅当p成立时,q成立;②要使q成立,必须且只需p成立.
对充要条件的词义表达要熟悉.如“当且仅当”“必须且只需”“等价于”“反之亦成立”等.
二、提升新知·注重综合
(1)方程x2+x+m=0无实根 Δ=1-4m<0 m>.故选B.
(2)a2+b2>0,则a,b不同时为零;a,b中至少有一个不为零,则a2+b2>0.
例2、(1)“m>”是“一元二次方程x2+x+m=0无实数解”的 ( )
A.充分不必要条件 B.充要条件
C.必要不充分条件 D.既不充分也不必要条件
(2)a,b中至少有一个不为零的充要条件是( )
A.ab=0 B.ab>0 C.a2+b2=0 D.a2+b2>0
解析
题型二 充要条件的判断
B
D
二、提升新知·注重综合
方法总结
(1)如果p是q的充要条件,那么q也是p的充要条件,也就是说,如果p q,那么p与q互为充要条件.
(2)条件关系判定的常用结论:
题型二 充要条件的判断
条件p与结论q的关系 结论
p是q的充分不必要条件
p是q的必要不充分条件
p q,且q p,即p q p是q的充要条件
p是q的既不充分也不必要条件
变式训练
1.(2019·天津高考)设x∈R,则“0
C.充要条件 D.既不充分也不必要条件
B
解析:由“|x-1|<1”可得“0
题型二 充要条件的判断
2.已知a,b是实数,则“a>0且b>0”是“a+b>0且ab>0”的________条件.
解析:a>0且b>0 a+b>0且ab>0,a+b>0且ab>0 a>0且b>0,故填充要.
充要
3.下列各题中,哪些p是q的充要条件?
(1)p:x=1;q:x-1= ;
(2)p:-1≤x≤5;q:x≥-1且x≤5;
(3)p:三角形是等边三角形;q:三角形是等腰三角形;
(4)p:A∩B=A,q: UB UA.
解析: (1)当x=1时,x-1= 成立;
当x-1= 时,x=1或x=2.
∴p不是q的充要条件,p是q的充分不必要条件.
(2)∵-1≤x≤5 x≥-1且x≤5,
∴p是q的充要条件.
二、提升新知·注重综合
变式训练
题型二 充要条件的判断
3.下列各题中,哪些p是q的充要条件?
(1)p:x=1;q:x-1= ;
(2)p:-1≤x≤5;q:x≥-1且x≤5;
(3)p:三角形是等边三角形;q:三角形是等腰三角形;
(4)p:A∩B=A,q: UB UA.
解析:(3)∵等边三角形一定是等腰三角形,而等腰三角形不一定都是等边三角形,
∴p不是q的充要条件,p是q的充分不必要条件.
(4)∵A∩B=A A B UB UA,
∴p是q的充要条件.
二、提升新知·注重综合
变式训练
题型二 充要条件的判断
例3、已知a+b≠0,证明a2+b2-a-b+2ab=0成立的充要条件是a+b=1.
题型三 充要条件的证明
先证充分性:
若a+b=1,
则a2+b2-a-b+2ab=(a+b)2-(a+b)=1-1=0,即充分性成立.
再证必要性:若a2+b2-a-b+2ab=0,
则(a+b)2-(a+b)=(a+b)·(a+b-1)=0.
∵a+b≠0,∴a+b-1=0,
即a+b=1成立,
综上,a2+b2-a-b+2ab=0成立的充要条件是a+b=1.
解析
二、提升新知·注重综合
二、提升新知·注重综合
方法总结
(1)先寻找必要条件,即将探求充要条件的对象视为结论,寻找使之成立的条件;再证明此条件是该对象的充分条件,即从充分性和必要性两方面说明.
(2)将原命题进行等价变形或转换,直至获得其成立的充要条件,探求的过程同时也是证明的过程,因为探求过程每一步都是等价的,所以不需要将充分性和必要性分开来证.
探求充要条件一般有两种方法
题型三 充要条件的证明
已知x,y都是非零实数,且x>y,求证:的充要条件是xy>0.
证明:(1)必要性:由,得,即,
又由x>y,得y-x<0,所以xy>0.
(2)充分性:由xy>0及x>y,得,即.
综上所述, 的充要条件是xy>0.
二、提升新知·注重综合
变式训练
题型三 充要条件的证明
例4、 已知p:-2≤x≤10,q:1-m≤x≤1+m(m>0),若p是q的必要不充分条件,求实数m的取值范围.
解析:p:-2≤x≤10,q:1-m≤x≤1+m(m>0).
因为p是q的必要不充分条件,
所以q是p的充分不必要条件,
即{x|1-m≤x≤1+m} {x|-2≤x≤10},
故有或
解得m≤3.
又m>0,所以实数m的取值范围为(0,3].
二、提升新知·注重综合
题型四 充分条件与必要条件应用
二、提升新知·注重综合
方法总结
(1)应用:可利用充分性与必要性进行相关问题的求解,特别是求参数的值或取值范围问题.
(2)求解步骤:先把p,q等价转化,利用充分条件、必要条件与集合间的包含关系,建立关于参数的不等式(组)进行求解.
(3)关键点:利用充分条件、必要条件求参数的取值范围的关键就是找出集合间的包含关系,要注意范围的临界值.
充分条件与必要条件的应用技巧
题型四 充分条件与必要条件应用
二、提升新知·注重综合
变式训练
题型四 充分条件与必要条件应用
例4、 已知p:-2≤x≤10,q:1-m≤x≤1+m(m>0),若p是q的必要不充分条件,求实数m的取值范围.
1.[变条件]若本例中“p是q的必要不充分条件”改为“p是q的充分不必要条件”,其他条件不变,求实数m的取值范围.
解析:p:-2≤x≤10,q:1-m≤x≤1+m(m>0).
因为p是q的充分不必要条件,
设p代表的集合为A,q代表的集合为B,所以AB.
所以或解得m≥9,
即实数m的取值范围是[9,+∞).
二、提升新知·注重综合
变式训练
题型四 充分条件与必要条件应用
例4、 已知p:-2≤x≤10,q:1-m≤x≤1+m(m>0),若p是q的必要不充分条件,求实数m的取值范围.
2.[变问法]本例中p,q不变,是否存在实数m使p是q的充要条件?若存在,求出m的值;若不存在,说明理由.
解析:因为p:-2≤x≤10,q:1-m≤x≤1+m(m>0).
若p是q的充要条件,则方程组无解.
故不存在实数m,使得p是q的充要条件.
当堂练习
1.设x∈R,则“1
C.充要条件 D.既不充分也不必要条件
一、基础经典题
解析:“1
三、训练素养·注重应用、创新
2.“x=1是x2-4x+3=0”的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
A
解析:若x=1,则x2-4x+3=0,是充分条件,若x2-4x+3=0,则x=1或x=3,不是必要条件.故选A.
当堂练习
3.下面四个条件中,使a>b成立的充分不必要条件是 ( )
A.a≥b+1 B.a>b-1
C.a2>b2 D.a3>b3
解析:由a≥b+1>b,从而a≥b+1 a>b;反之,如a=4,b=3.5,则4>3.5 3.5+1,故a>b a≥b+1,故A正确.
A
三、训练素养·注重应用、创新
4.王大妈在地摊上因为贪图便宜买了劣质商品,非常气愤地说了句“真是便宜没好货”,按照王大妈的理解,“好货”是“不便宜”的________________条件.
解析:“好货不便宜”是“便宜没好货”的逆否命题,
根据互为逆否命题的真假一致得到:“好货不便宜”是真命题.
所以“好货” “不便宜”,
所以“好货”是“不便宜”的充分不必要条件.
充分不必要
当堂练习
5.条件p:1-x<0,条件q:x>a,若p是q的充分不必要条件,求a的取值范围.
解析:p:x>1,若p是q的充分不必要条件,则p q,但qp,也就是说,p对应集合是q对应集合的真子集,所以a<1,即a的取值范围为(-∞,1).
二、创新应用题
三、训练素养·注重应用、创新
