人教B版(2019)数学必修第三册综合复习:同角三角函数的基本关系及诱导公式达标训练(含答案)
文档属性
| 名称 | 人教B版(2019)数学必修第三册综合复习:同角三角函数的基本关系及诱导公式达标训练(含答案) |
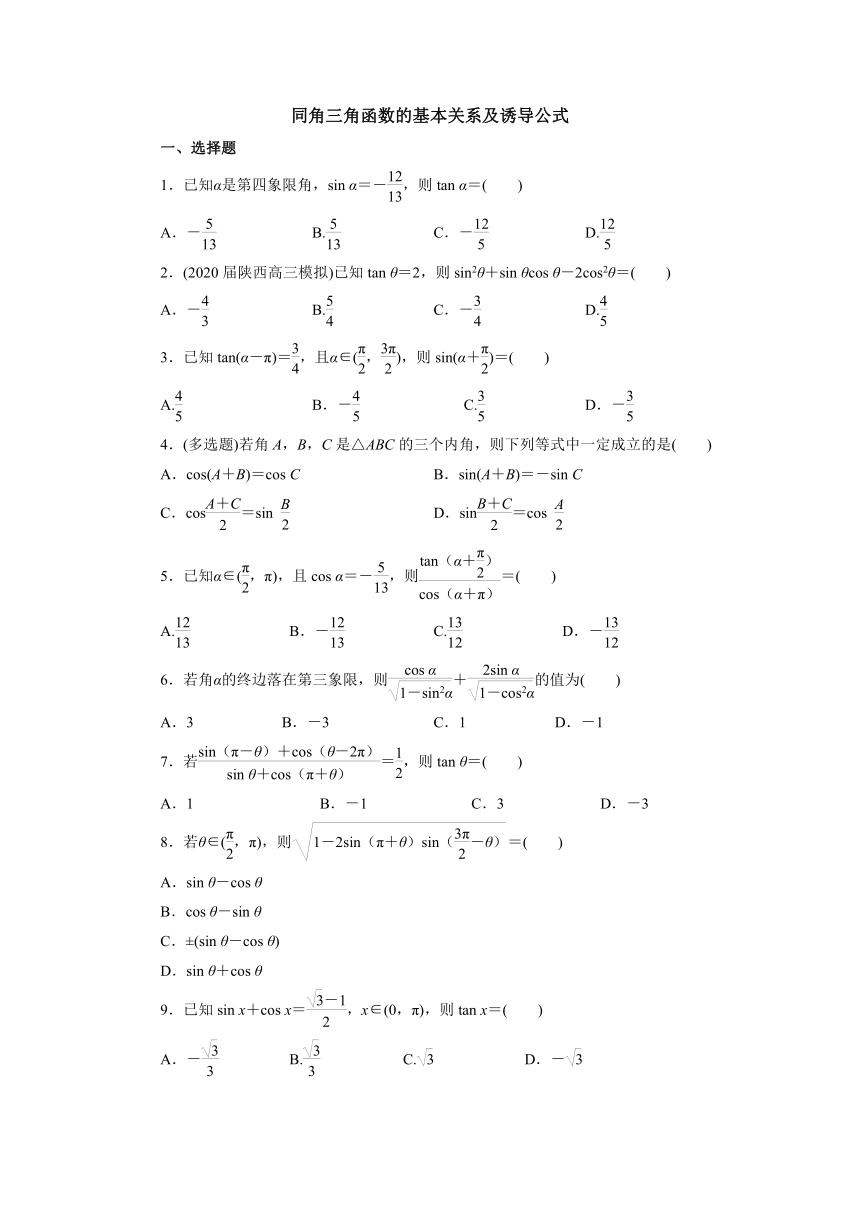
|
|
| 格式 | docx | ||
| 文件大小 | 25.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 00:00:00 | ||
图片预览
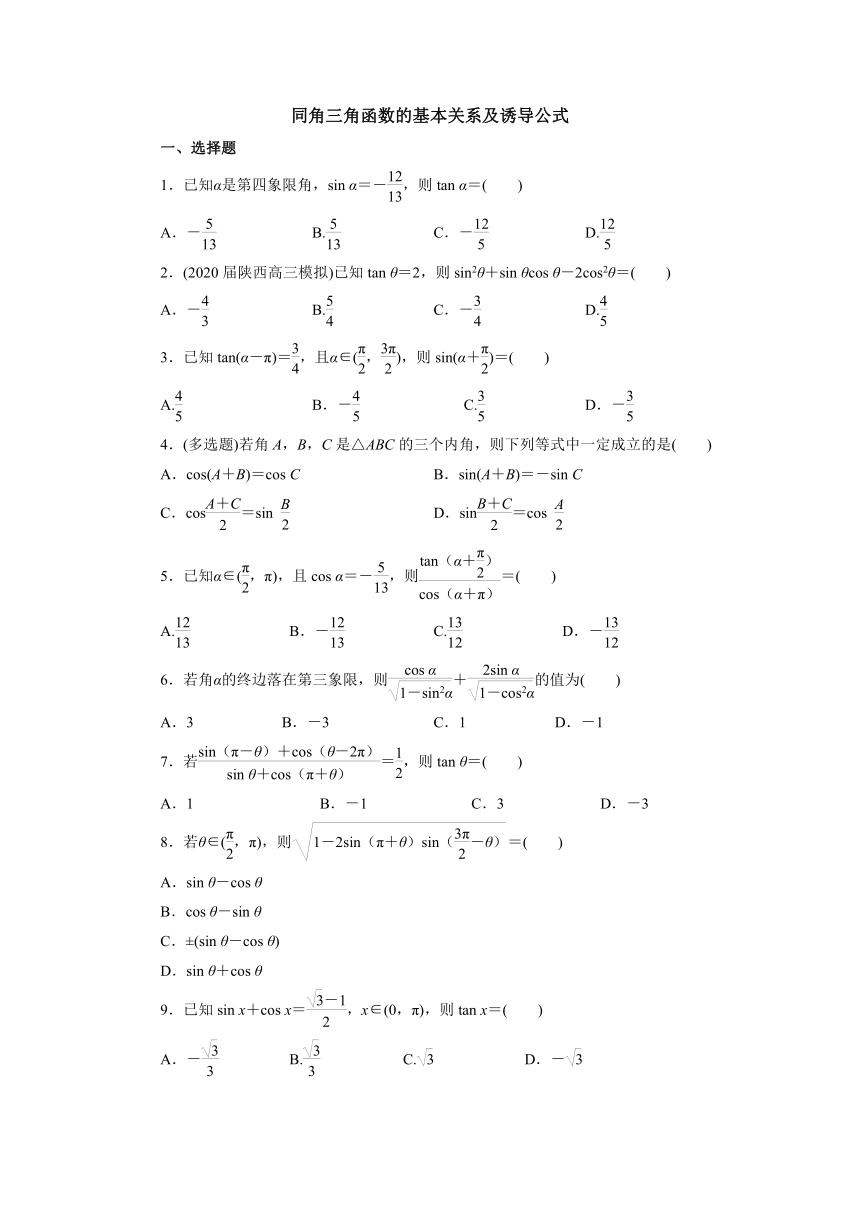

文档简介
同角三角函数的基本关系及诱导公式
一、选择题
1.已知α是第四象限角,sin α=-,则tan α=( )
A.- B. C.- D.
2.(2020届陕西高三模拟)已知tan θ=2,则sin2θ+sin θcos θ-2cos2θ=( )
A.- B. C.- D.
3.已知tan(α-π)=,且α∈(,),则sin(α+)=( )
A. B.- C. D.-
4.(多选题)若角A,B,C是△ABC的三个内角,则下列等式中一定成立的是( )
A.cos(A+B)=cos C B.sin(A+B)=-sin C
C.cos=sin D.sin=cos
5.已知α∈(,π),且cos α=-,则=( )
A. B.- C. D.-
6.若角α的终边落在第三象限,则+的值为( )
A.3 B.-3 C.1 D.-1
7.若=,则tan θ=( )
A.1 B.-1 C.3 D.-3
8.若θ∈(,π),则=( )
A.sin θ-cos θ
B.cos θ-sin θ
C.±(sin θ-cos θ)
D.sin θ+cos θ
9.已知sin x+cos x=,x∈(0,π),则tan x=( )
A.- B. C. D.-
10.(2020·福建三明模拟)已知cos(75°+α)=,则sin(α-15°)+cos(105°-α)的值是( )
A. B.-
C. D.-
二、填空题
11.计算:sin 750°=________.
12.(2020届浙江台州一中高三月考)若sin(π-α)=-2sin(+α),则sin α·cos α=________.
13.已知sin α=,α∈(0,),则cos(π-α)=________,cos 2α=________.
14.(2020届辽宁葫芦岛第六高级中学高三月考)已知α为第二象限角,则cos α+sin α·=________.
15.已知sin θ+cos θ=,θ∈(0,),则sin θ-cos θ的值为________.
16.(2020届河北张家口高三月考)已知0<α<,若cos α-sin α=-,则的值为________.
三、解答题
17.已知关于x的方程2x2-(+1)x+m=0的两根为sin θ和cos θ,θ∈(0,2π).求:
(1)+的值;
(2)m的值;
(3)方程的两根及此时θ的值.
参考答案
1.C
解析:因为α是第四象限角,sin α=-,所以cos α==,故tan α==-.故选C.
2.D
解析:sin2θ+sin θcos θ-2cos2θ===.故选D.
3.B
解析:tan(α-π)=tan α=.由解得cos α=±.又因为α∈,所以α为第三象限的角,所以cos α=-,所以sin=cos α=-.故选B.
4.CD
解析:因为A+B+C=π,所以A+B=π-C,=,=,所以cos(A+B)=cos(π-C)=-cos C,sin(A+B)=sin(π-C),cos=cos-=sin,sin=sin-=cos .故选CD.
5.C
解析:因为α∈,且cos α=-,所以sin α==,所以===.故选C.
6.B
解析:由角α的终边落在第三象限,得sin α<0,cos α<0,故原式=+=+=-1-2=-3.故选B.
7.D
解析:由已知得,=,∴=,故tan θ=-3.故选D.
8.A
解析:因为===|sin θ-cos θ|,θ∈,所以sin θ-cos θ>0,所以原式=sin θ-cos θ.故选A.
9.D
解析:sin x+cos x=,x∈(0,π),则(sin x+cos x)2=.因为sin2x+cos2x=1,所以2sin xcos x=-,即==-,解得tan x=-或tan x=-.当tan x=-时,sin x+cos x<0,不合题意,舍去,所以tan x=-.故选D.
10.D
解析: sin(α-15°)+cos(105°-α)=sin[(75°+α)-90°]+cos[180°-(75°+α)]=-cos(75°+α)-cos(75°+α)=-2cos(75°+α)=-,故选D.
11.
解析:sin 750°=sin(720°+30°)=sin 30°=.
12.-
解析:由sin(π-α)=-2sin,可得sin α=-2cos α,则tan α=-2,所以sin α·cos α===-.
13.-
解析:cos(π-α)=-cos α=-=-,cos 2α=cos2α-sin2α=-2-2=.
14.0
解析:原式=cos α+sin α=cos α+sin α.因为α是第二象限角,所以sin α>0,cos α<0,
所以cos α+sin α=-1+1=0,即原式等于0.
15.-
解析:∵sin θ+cos θ=,∴sin θcos θ=.∵(sin θ-cos θ)2=1-2sin θcos θ=,θ∈,∴sin θ-cos θ=-.
16.
解析:因为cos α-sin α=-,①所以1-2sin αcos α=,即2sin αcos α=.所以(sin α+cos α)2=1+2sin αcos α=1+=.又0<α<,所以sin α+cos α>0.所以sin α+cos α=.②由①②得sin α=,cos α=,tan α=2,所以=.
17.解:(1)原式=+=+==sin θ+cos θ.
由条件知sin θ+cos θ=,故+=.
(2)由sin2θ+2sin θcos θ+cos2θ=1+2sin θcos θ,
即(sin θ+cos θ)2=1+2×,解得m=.
(3)由
解得或
又θ∈(0,2π),故θ=或θ=.
一、选择题
1.已知α是第四象限角,sin α=-,则tan α=( )
A.- B. C.- D.
2.(2020届陕西高三模拟)已知tan θ=2,则sin2θ+sin θcos θ-2cos2θ=( )
A.- B. C.- D.
3.已知tan(α-π)=,且α∈(,),则sin(α+)=( )
A. B.- C. D.-
4.(多选题)若角A,B,C是△ABC的三个内角,则下列等式中一定成立的是( )
A.cos(A+B)=cos C B.sin(A+B)=-sin C
C.cos=sin D.sin=cos
5.已知α∈(,π),且cos α=-,则=( )
A. B.- C. D.-
6.若角α的终边落在第三象限,则+的值为( )
A.3 B.-3 C.1 D.-1
7.若=,则tan θ=( )
A.1 B.-1 C.3 D.-3
8.若θ∈(,π),则=( )
A.sin θ-cos θ
B.cos θ-sin θ
C.±(sin θ-cos θ)
D.sin θ+cos θ
9.已知sin x+cos x=,x∈(0,π),则tan x=( )
A.- B. C. D.-
10.(2020·福建三明模拟)已知cos(75°+α)=,则sin(α-15°)+cos(105°-α)的值是( )
A. B.-
C. D.-
二、填空题
11.计算:sin 750°=________.
12.(2020届浙江台州一中高三月考)若sin(π-α)=-2sin(+α),则sin α·cos α=________.
13.已知sin α=,α∈(0,),则cos(π-α)=________,cos 2α=________.
14.(2020届辽宁葫芦岛第六高级中学高三月考)已知α为第二象限角,则cos α+sin α·=________.
15.已知sin θ+cos θ=,θ∈(0,),则sin θ-cos θ的值为________.
16.(2020届河北张家口高三月考)已知0<α<,若cos α-sin α=-,则的值为________.
三、解答题
17.已知关于x的方程2x2-(+1)x+m=0的两根为sin θ和cos θ,θ∈(0,2π).求:
(1)+的值;
(2)m的值;
(3)方程的两根及此时θ的值.
参考答案
1.C
解析:因为α是第四象限角,sin α=-,所以cos α==,故tan α==-.故选C.
2.D
解析:sin2θ+sin θcos θ-2cos2θ===.故选D.
3.B
解析:tan(α-π)=tan α=.由解得cos α=±.又因为α∈,所以α为第三象限的角,所以cos α=-,所以sin=cos α=-.故选B.
4.CD
解析:因为A+B+C=π,所以A+B=π-C,=,=,所以cos(A+B)=cos(π-C)=-cos C,sin(A+B)=sin(π-C),cos=cos-=sin,sin=sin-=cos .故选CD.
5.C
解析:因为α∈,且cos α=-,所以sin α==,所以===.故选C.
6.B
解析:由角α的终边落在第三象限,得sin α<0,cos α<0,故原式=+=+=-1-2=-3.故选B.
7.D
解析:由已知得,=,∴=,故tan θ=-3.故选D.
8.A
解析:因为===|sin θ-cos θ|,θ∈,所以sin θ-cos θ>0,所以原式=sin θ-cos θ.故选A.
9.D
解析:sin x+cos x=,x∈(0,π),则(sin x+cos x)2=.因为sin2x+cos2x=1,所以2sin xcos x=-,即==-,解得tan x=-或tan x=-.当tan x=-时,sin x+cos x<0,不合题意,舍去,所以tan x=-.故选D.
10.D
解析: sin(α-15°)+cos(105°-α)=sin[(75°+α)-90°]+cos[180°-(75°+α)]=-cos(75°+α)-cos(75°+α)=-2cos(75°+α)=-,故选D.
11.
解析:sin 750°=sin(720°+30°)=sin 30°=.
12.-
解析:由sin(π-α)=-2sin,可得sin α=-2cos α,则tan α=-2,所以sin α·cos α===-.
13.-
解析:cos(π-α)=-cos α=-=-,cos 2α=cos2α-sin2α=-2-2=.
14.0
解析:原式=cos α+sin α=cos α+sin α.因为α是第二象限角,所以sin α>0,cos α<0,
所以cos α+sin α=-1+1=0,即原式等于0.
15.-
解析:∵sin θ+cos θ=,∴sin θcos θ=.∵(sin θ-cos θ)2=1-2sin θcos θ=,θ∈,∴sin θ-cos θ=-.
16.
解析:因为cos α-sin α=-,①所以1-2sin αcos α=,即2sin αcos α=.所以(sin α+cos α)2=1+2sin αcos α=1+=.又0<α<,所以sin α+cos α>0.所以sin α+cos α=.②由①②得sin α=,cos α=,tan α=2,所以=.
17.解:(1)原式=+=+==sin θ+cos θ.
由条件知sin θ+cos θ=,故+=.
(2)由sin2θ+2sin θcos θ+cos2θ=1+2sin θcos θ,
即(sin θ+cos θ)2=1+2×,解得m=.
(3)由
解得或
又θ∈(0,2π),故θ=或θ=.
