人教A版(2019)高中数学选择性必修第三册 8.3.2独立性检验 课件(共24张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第三册 8.3.2独立性检验 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 484.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 16:11:20 | ||
图片预览








文档简介
(共24张PPT)
成对数据的统计分析
第八章
8.3.2 独立性检验
8.3 列联表与独立性检验
课前 预习案
1.零假设H0或原假设:分类变量X和Y独立.
2.公式:χ2=________________________.
独立性检验
3.临界值:忽略χ2的实际分布与该近似分布的误差后,对于任何小概率值α,可以找到相应的正实数xα,使下面关系式成立:
P(χ2≥xα)=α.
我们称xα为α的临界值,这个临界值可作为判断χ2大小的标准.概率值α越小,临界值xα越大.
4.独立性检验
基于小概率值α的检验规则是:
当_________时,我们就推断H0_________,即认为X和Y_________,就推断犯错误的概率__________;
当_________时,我们_______充分证据推断H0不成立,可以认为X和Y_______.
这种利用χ2的取值推断分类变量X和Y是否独立的方法称为χ2独立性检验,读作“_________________”,简称独立性检验.
χ2≥xα
不成立
不独立
不超过α
χ2没有
独立
卡方独立性检验
1.判断下列说法是否正确,正确的在它后面的括号里打“√”,错误的打“×”.
(1)在独立性检验中,若χ2越大,则两个分类变量有关系的可能性越大.
( )
(2)应用独立性检验的基本思想对两个变量间的关系作出的推断一定是正确的.
( )
答案 (1)√ (2)×
2.在一项中学生近视情况的调查中,某校男生150名中有80名近视,女生140名中有70名近视,在检验这些中学生眼睛近视是否与性别有关时用什么方法最有说服力 ( )
A.平均数与方差 B.回归分析
C.独立性检验 D.概率
答案 C
解析 判断两个分类变量是否有关的最有效方法是进行独立性检验.
3.根据下表计算:
χ2≈____________(保留3位小数).
答案 4.514
不看电视 看电视
男 37 85
女 35 143
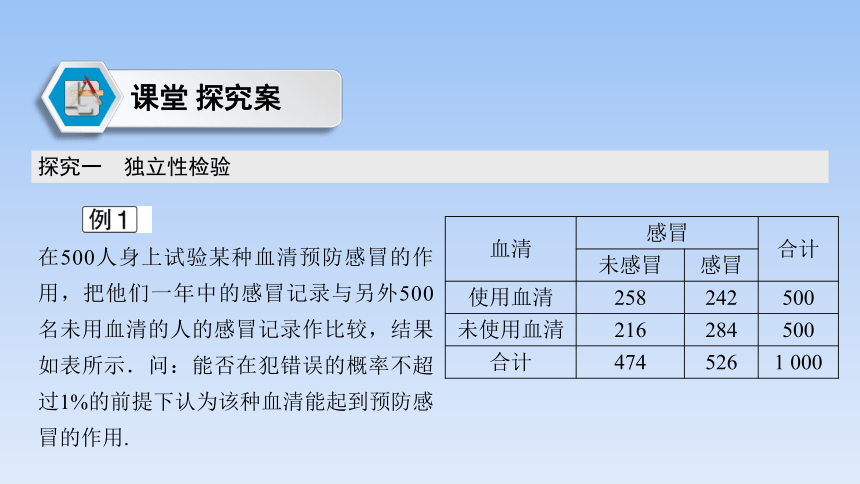
在500人身上试验某种血清预防感冒的作用,把他们一年中的感冒记录与另外500名未用血清的人的感冒记录作比较,结果如表所示.问:能否在犯错误的概率不超过1%的前提下认为该种血清能起到预防感冒的作用.
课堂 探究案
探究一 独立性检验
血清 感冒 合计
未感冒 感冒 使用血清 258 242 500
未使用血清 216 284 500
合计 474 526 1 000
[方法总结] 独立性检验的一般步骤
(1)提出零假设H0:X和Y相互独立,并给出在问题中的解释;
(2)根据抽样数据整理出2×2列联表,计算χ2的值,并与临界值xα比较;
(3)根据检验规则得出推断结论;
(4)在X和Y不独立的情况下,根据需要,通过比较相应的频率,分析X和Y间的影响规律.
[训练1] 调查在2~3级风的海上航行中男女乘客的晕船情况,结果如表所示:
根据此资料,你是否认为在2~3级风的海上航行中男人比女人更容易晕船?
性别 晕船 合计
晕船 不晕船 男人 12 25 37
女人 10 24 34
合计 22 49 71
探究二 独立性检验的应用
[变式1] 根据(2)的结论,本次被调查的人中,至少有多少人的休闲方式是运动?
[变式2] 若增加条件n=100,问能否在犯错误不超过0.1的前提下,可认为“性别与休闲方式有关”?
[方法总结] 运用独立性检验的方法
(1)列出2×2列联表,根据公式计算χ2.
(2)根据临界值作出判断.
[训练2] 为了解某品种一批树苗生长情况,在该批树苗中随机抽取了容量为120的样本,测量树苗高度(单位:cm),经统计,其高度均在区间[19,31]内,将其按[19,21),[21,23),[23,25),[25,27),[27,29),[29,31]分成6组,制成如图所示的频率分布直方图.其中高度为27 cm及以上的树苗为优质树苗.
(1)求图中a的值,并估计这批树苗的平均高度(同一组中的数据用该组区间的中点值作代表);
(2)已知所抽取的这120棵树苗来自于A,B两个试验区,部分数据如下列联表:
树苗 试验区 合计
A试验区 B试验区 优质树苗 20
非优质树苗 60
合计
将列联表补充完整,并判断是否有99.9%的把握认为优质树苗与A,B两个试验区有关系,并说明理由.
成对数据的统计分析
第八章
8.3.2 独立性检验
8.3 列联表与独立性检验
课前 预习案
1.零假设H0或原假设:分类变量X和Y独立.
2.公式:χ2=________________________.
独立性检验
3.临界值:忽略χ2的实际分布与该近似分布的误差后,对于任何小概率值α,可以找到相应的正实数xα,使下面关系式成立:
P(χ2≥xα)=α.
我们称xα为α的临界值,这个临界值可作为判断χ2大小的标准.概率值α越小,临界值xα越大.
4.独立性检验
基于小概率值α的检验规则是:
当_________时,我们就推断H0_________,即认为X和Y_________,就推断犯错误的概率__________;
当_________时,我们_______充分证据推断H0不成立,可以认为X和Y_______.
这种利用χ2的取值推断分类变量X和Y是否独立的方法称为χ2独立性检验,读作“_________________”,简称独立性检验.
χ2≥xα
不成立
不独立
不超过α
χ2
独立
卡方独立性检验
1.判断下列说法是否正确,正确的在它后面的括号里打“√”,错误的打“×”.
(1)在独立性检验中,若χ2越大,则两个分类变量有关系的可能性越大.
( )
(2)应用独立性检验的基本思想对两个变量间的关系作出的推断一定是正确的.
( )
答案 (1)√ (2)×
2.在一项中学生近视情况的调查中,某校男生150名中有80名近视,女生140名中有70名近视,在检验这些中学生眼睛近视是否与性别有关时用什么方法最有说服力 ( )
A.平均数与方差 B.回归分析
C.独立性检验 D.概率
答案 C
解析 判断两个分类变量是否有关的最有效方法是进行独立性检验.
3.根据下表计算:
χ2≈____________(保留3位小数).
答案 4.514
不看电视 看电视
男 37 85
女 35 143
在500人身上试验某种血清预防感冒的作用,把他们一年中的感冒记录与另外500名未用血清的人的感冒记录作比较,结果如表所示.问:能否在犯错误的概率不超过1%的前提下认为该种血清能起到预防感冒的作用.
课堂 探究案
探究一 独立性检验
血清 感冒 合计
未感冒 感冒 使用血清 258 242 500
未使用血清 216 284 500
合计 474 526 1 000
[方法总结] 独立性检验的一般步骤
(1)提出零假设H0:X和Y相互独立,并给出在问题中的解释;
(2)根据抽样数据整理出2×2列联表,计算χ2的值,并与临界值xα比较;
(3)根据检验规则得出推断结论;
(4)在X和Y不独立的情况下,根据需要,通过比较相应的频率,分析X和Y间的影响规律.
[训练1] 调查在2~3级风的海上航行中男女乘客的晕船情况,结果如表所示:
根据此资料,你是否认为在2~3级风的海上航行中男人比女人更容易晕船?
性别 晕船 合计
晕船 不晕船 男人 12 25 37
女人 10 24 34
合计 22 49 71
探究二 独立性检验的应用
[变式1] 根据(2)的结论,本次被调查的人中,至少有多少人的休闲方式是运动?
[变式2] 若增加条件n=100,问能否在犯错误不超过0.1的前提下,可认为“性别与休闲方式有关”?
[方法总结] 运用独立性检验的方法
(1)列出2×2列联表,根据公式计算χ2.
(2)根据临界值作出判断.
[训练2] 为了解某品种一批树苗生长情况,在该批树苗中随机抽取了容量为120的样本,测量树苗高度(单位:cm),经统计,其高度均在区间[19,31]内,将其按[19,21),[21,23),[23,25),[25,27),[27,29),[29,31]分成6组,制成如图所示的频率分布直方图.其中高度为27 cm及以上的树苗为优质树苗.
(1)求图中a的值,并估计这批树苗的平均高度(同一组中的数据用该组区间的中点值作代表);
(2)已知所抽取的这120棵树苗来自于A,B两个试验区,部分数据如下列联表:
树苗 试验区 合计
A试验区 B试验区 优质树苗 20
非优质树苗 60
合计
将列联表补充完整,并判断是否有99.9%的把握认为优质树苗与A,B两个试验区有关系,并说明理由.
