人教A版(2019)高中数学选择性必修第三册 《成对数据的统计分析》单元测试(一)(含解析)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第三册 《成对数据的统计分析》单元测试(一)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 16:19:45 | ||
图片预览




文档简介
《成对数据的统计分析》单元测试(一)
一、选择题
1.已知x,y是两个变量,下列四个关系中,x,y呈负相关的是( )
A.
B.
C.
D.
2.如果两个变量之间的线性相关程度很高,则其相关系数r的绝对值应接近于( )
A.0.5
B.2
C.0
D.1
3.两个变量的散点图如图,可考虑用如下函数进行拟合比较合理的是( )
A.
B.
C.
D.
4.一位母亲记录了儿子3~9岁的身高,数据(略),由此建立的身高与年龄的回归模型为,用这个模型预测这个孩子10岁时的身高,则正确的叙述是( )
A.身高一定是145.83cm
B.身高在145.83cm以上
C.身高在145.83cm左右
D.身高在145.83cm以下
5.在一组样本数据的散点图中,若所有样本点都在直线上,则这组样本数据的样本相关系数为( )
A.
B.0
C.
D.1
6.已知变量x与y正相关,且由观测数据算得样本平均数,则由该观测的数据算得的经验回归方程可能是( )
A.
B.
C.
D.
7.为了研究高中学生对乡村音乐的态度(喜欢和不喜欢两种态度)与性别的关系,运用2×2列联表进行独立性检验,经计算得=7.01,则认为“喜欢乡村音乐与性别有关系”的把握约为( )
A.0.1%
B.1%
C.99%
D.99.9%
8.某研究所为了检验某血清预防感冒的作用,把500名使用了该血清的志愿者与另外500名未使用该血清的志愿者一年中的感冒记录作比较,提出假设:“这种血清不能起到预防感冒的作用”,利用2×2列联表计算得≈3.918,经查临界值表知P(≥3.841)=0.05.则下列叙述中正确的是( )
A.有95%的把握认为“这种血清能起到预防感冒的作用”
B.若有人未使用该血清,那么他一年中有95%的可能性得感冒
C.这种血清预防感冒的有效率为95%
D.这种血清预防感冒的有效率为5%
9.在吸烟与患肺病这两个分类变量的计算中,下列说法正确的是( )
A.若>6.635,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病
B.从独立性检验可知,有99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有99%的可能患有肺病
C.若从统计量中得出有95%的把握认为吸烟与患肺病有关系,是指有5%的可能性使得推断出现错误
D.以上三种说法都不正确
10.根据如下样本数据
x 3 4 5 6 7 8
y 4.0 2.5 -0.5 0.5 -2.0 -3.0
得到的经验回归方程为,则( )
A.
B.
C.
D.
11.某化工厂为预测某产品的回收率y,需要研究它和原料有效成分含量x之间的相关关系,现取了8对观测值,计算得,则y与x的回归直线方程是( )
A.
B.
C.
D.
12.已知变量y关于x的经验回归方程为,其一组数据如下表所示.
x 1 2 3 4
y e
若x=5,则预测y的值可能为( )
A.
B.
C.
D.
二、填空题
13.以模型去拟合一组数据时,为了求出回归方程,设之,其变换后得到线性回归方程z=0.3x+4,则c=_________.
14.已知第一组样本点为(-5,-8.9),(-4,-7.2),(-3,-4.8),(-2,-3.3),(-1,-0.9),其变量间的相关系数为;第二组样本点为(1,8.9),(2,7.2),(3,4.8),(4,3.3),(5,0.9)其变量间的相关系数为.则,的大小关系为_________.
15.高三年级267位学生参加期末考试,某班37位学生的语文成绩,数学成绩与总成绩在全年级中的排名情况如下,甲、乙、丙为该班三位学生.
从这次考试成绩看:
(1)在甲、乙两人中,其语文成绩名次比其总成绩名次靠前的学生是_________.
(2)在语文和数学两个科目中,丙同学的成绩名次更靠前的科目是_________.
16.某班主任对全班50名学生作了一次调查,所得数据如表:
0.05 0.01
3.841 6.635
认为作业多 认为作业不多 总计
喜欢玩电脑游戏 18 9 27
不喜欢玩电脑游戏 8 15 23
总计 26 24 50
由表中数据计算得到≈5.059,于是___________(填“能”或“不能”)在犯错误的概率不超过0.01的前提下认为喜欢玩电脑游戏与认为作业多有关.
三、解答题
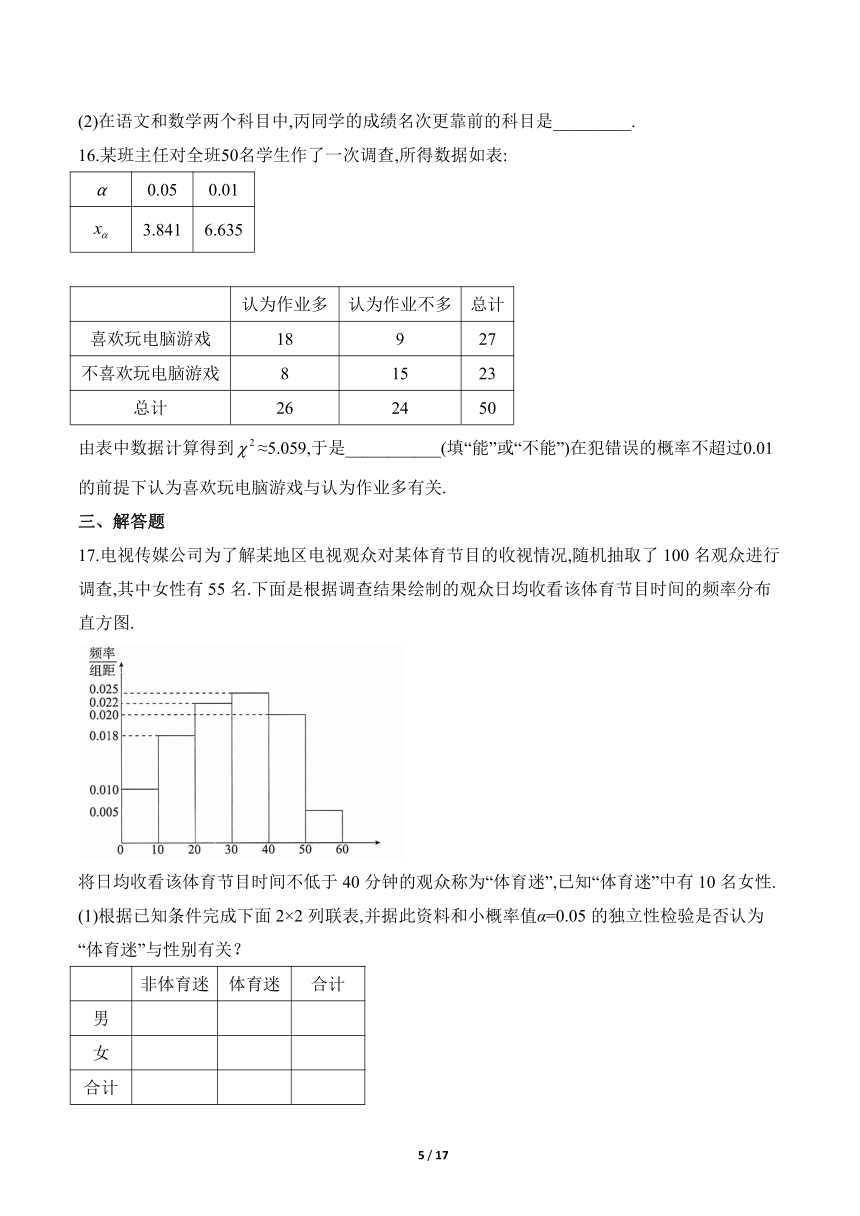
17.电视传媒公司为了解某地区电视观众对某体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图.
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性.
(1)根据已知条件完成下面2×2列联表,并据此资料和小概率值α=0.05的独立性检验是否认为“体育迷”与性别有关?
非体育迷 体育迷 合计
男
女
合计
(2)将日均收看该体育节目不低于50分钟的观众称为“超级体育迷”,已知“超级体育迷”中有2名女性.若从“超级体育迷”中任意选取2人,求至少有1名女性观众的概率.
附:.
0.050 0.010 0.001
3.841 6.635 10.825
18.(2018·全国卷Ⅲ改编)某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图.
(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;
(2)求40名工人完成生产任务所需时间的中位数m,并将完成生产任务所需时间超过m和不超过m的工人数填入下面的列联表:
超过m 不超过m
第一种生产方式
第二种生产方式
(3)根据(2)中的列联表,和小概率值α=0.1的独立性检验,是否认为两种生产方式的效率有差异?
附:
a 0.050 0.010 0.001
3.841 6.635 10.825
19.(2017·全国卷Ⅱ改编)海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取100个网箱,测量各箱水产品的产量(单位:kg),其频率分布直方图如下:
(1)设两种养殖方法的箱产量相互独立,记A表示事件“旧养殖法的箱产量低于50kg,新养殖法的箱产量不低于50kg”,估计A的概率;
(2)填写下面列联表,并根据小概率值α=0.01的独立性检验,是否认为箱产量与养殖方法有关.
箱产量<50kg
旧养殖法
新养殖法
(3)根据箱产量的频率分布直方图,求新养殖法箱产量的中位数的估计值(精确到0.01).
附:
0.050 0.010 0.001
3.841 6.635 10.828
.
20.(12分)近年来,国资委、党委高度重视扶贫开发工作,坚决贯彻落实中央扶贫工作重大决策部署,在各个贫困县全力推进定点扶贫各项工作,取得了积极成效,某贫困县为了响应国家精准扶贫的号召,特地承包了一块土地,已知土地的使用面积以及相应的管理时间的关系如下表所示:
土地使用面积x(单位:亩) 1 2 3 4 5
管理时间y(单位:月) 8 10 13 25 24
并调查了某村300名村民参与管理的意愿,得到的部分数据如下表所示:
愿意参与管理 不愿意参与管理
男性村民 150 50
女性村民 50
(1)求出相关系数r的大小,并判断管理时间y(月)与土地使用面积x(亩)是否线性相关?
(2)根据小概率值α=0.001的独立性检验,是否认为村民的性别与参与管理的意愿具有相关性?
参考公式:
.
临界值表:
0.100 0.050 0.025 0.010 0.001
2.706 3.841 5.024 6.635 10.828
参考数据:
21.某企业新研发了一种产品,产品的成本由原料成本及非原料成本组成.每件产品的非原料成本y(元)与生产该产品的数量x(千件)有关,经统计得到如下数据.
x 1 2 3 4 5 6 7 8
y 112 61 44.5 35 30.5 28 25 24
根据以上数据,绘制了散点图.
观察散点图,两个变量不具有线性相关关系,现考虑用反比例函数模型和指数函数模型分别对两个变量的关系进行拟合.已求得用指数函数模型拟合的回归方程为,lny与x的相关系数=-0.94.
(1)用反比例函数模型求y关于x的经验回归方程;
(2)用相关系数判断上述两个模型哪一个拟合效果更好(精确到0.01),并用其估计产量为10千件时每件产品的非原料成本;
(3)该企业采取订单生产模式(根据订单数量进行生产,即产品全部售出).根据市场调研数据,若该产品单价定为100元,则签订9千件订单的概率为0.8,签订10千件订单的概率为0.2;若单价定为90元,则签订10千件订单的概率为0.3,签订11千件订单的概率为0.7.已知每件产品的原料成本为10元,根据(2)的结果,企业要想获得更高利润,产品单价应选择100元还是90元,请说明理由.
参考数据(其中):
183.4 0.34 0.115 1.53 360 22385.5 61.4 0.135
参考公式:对于一组数据,其回归直线的斜率和截距的最小二乘估计分别为:,相关系数
22.为研究质量x(单位:g)对弹簧长度y(单位:cm)的影响,对不同质量的6个物体进行测量,数据如表所示.
x 5 10 15 20 25 30
y 7.25 8.12 8.95 9.90 10.9 11.8
(1)作出散点图并求经验回归方程;
(2)求出并说明回归模型拟合的程度;
(3)进行残差分析.
答案解析
一、选择题
1.答案:D
解析:根据题意,依次分析选项:对于A,,当x增大时,y的值不一定减小,两个变量不是负相关,不符合题意;对于B,,当x增大时,y的值不一定减小,两个变量不是负相关,不符合题意;对于C,,当x增大时,y的值一定增大,两个变量正相关,不符合题意;对于D,,当x增大时,y的值一定减小,两个变量负相关,符合题意.
2.答案:D
解析:相关系数越接近于1,相关程度越高.
3.答案:B
解析:本题考查学生数学抽象、数学建模的核心素养.由散点图可知,此曲线类似对数函数型曲线,因此可用函数模型进行拟合.
4.答案:C
解析:将x的值代入回归方程,可以预测孩子10岁时的身高为83.
5.答案:D
解析:因为所有的点都在直线上,这组样本数据完全正相关,故其相关系数为1.
6.答案:A
解析:因为变量与正相关,所以排除选项C,D,又因为回归直线必过样本中心点(3,3.5),代入检验知,只有直线过点(3,3.5)
7.答案:C
解析:易知=7.01>6.635,对照临界值表知,有99%的把握认为喜欢乡村音乐与性别有关系.
8.答案:A
解析:≈3.918>3.841,因此有95%的把握认为“这种血清能起到预防感冒的作用”..
9.答案:C
解析:A,B是对的误解,99%的把握认为吸烟和患肺病有关,是指通过大量的观察试验得出的一个数值,并不是100个人中必有99个人患肺病,也可能这100个人全健康.
10.答案:B
解析:依题意,画散点图知,两个变量负相关,所以b<0,a>0.
11.答案:A
解析:由题意知,,
则,
.
12.答案:D
解析:将式子两边取对数,得到,令,得到,列出x,z的取值对应的表格,
x 1 2 3 4
z 1 3 4 6
则,
,
解得,当x=5时,.
二、填空题
13.答案:
解析:,两边取对数.可得,
令z=lny,可得.
14.答案:>
解析:由第1组数据可知,两变量间成正相关,故>0,由第2组数据可知,两变量间成负相关,故<0,故>0>.
15.答案:乙;数学
解析:数学①由图可知,甲的语文成绩排名比总成绩排名靠后;而乙的语文成绩排名比总成绩排名靠前,故填乙.②由图可知,比丙的数学成绩排名还靠后的人比较多;而总成绩的排名中比丙排名靠后的人数比较少,所以丙的数学成绩的排名更靠前.
16.答案:不能
解析:查表知若要在犯错误的概率不超过0.01的前提下认为喜欢玩电脑游戏与认为作业多有关,则临界值=6.635.本题中,k≈5.059<6.635,所以不能在犯错误的概率不超过0.01的前提下认为喜欢玩电脑游戏与认为作业多有关.
三、解答题
17.答案:见解析
解析:(1)零假设为:“体育迷”与性别无关.由频率颁布直方图可知,在抽取的100人中,“体育迷”有25人,从而2×2列联表如下:
非体育迷 体育迷 合计
男 30 15 45
女 45 10 55
合计 75 25 100
由2×2列联表中数据代入公式计算,得:
=.
因为3.030<3.841,所以,根据小概率值α=0.05的独立检验,认为“体育迷”与性别有关.
(2)由频率分布直方图可知,“超级体育迷”为5人,从而一切可能结果所组成的基本事件空间
其中表示男生,
表示女生,j=1,2.由10个基本事件组成,而且这些事件的出现是等可能的.用A表示“任选2人中至少有1名是女性”这一事件,则A=
.
.
18.答案:见解析
解析:(1)第二种生产方式的效率更高.理由如下:
①由茎叶图可知:用第一种生产方式的工人中,有75%的工人完成生产任务所需时间至少80分钟,用第二种生产方式的工人中,有75%的工人完成生产任务所需时间至多79分钟.因此第二种生产方式的效率更高.
②由茎叶图可知:用第一种生产方式的工人完成生产任务所需时间的中位数为85.5分钟,用第二种生产方式的工人完成生产任务所需时间的中位数为73.5分钟.因此第二种生产方式的效率更高.
③由茎叶图可知:用第一种生产方式的工人完成生产任务平均所需时间高于80分钟;用第二种生产方式的工人完成生产任务平均所需时间低于80分钟,因此第二种生产方式的效率更高.
④由茎叶图可知:用第一种生产方式的工人完成生产任务所需时间分布在茎8上的最多,关于茎8大致呈对称分布;用第二种生产方式的工人完成生产任务所需时间分布在茎7上的最多,关于茎7大致呈对称分布,又用两种生产方式的工人完成生产任务所需时间分布的区间相同,故可以认为用第二种生产方式完成生产任务所需的时间比用第一种生产方式完成生产任务所需的时间更少,因此第二种生产方式的效率更高.
(2)由茎叶图知.列联表如下.
超过m 不超过m
第一种生产方式 15 5
第二种生产方式 5 15
(3)零假设:两种生产方式的效率没有差异.由于,所以根据小概率值α=0.1的独立性检验,判断不成立,即认为两种生产方式的效率有差异.
19.答案:见解析
解析:(1)记:“旧养殖法的箱产量低于50kg”为事件B,“新养殖法的箱产量不低于50kg”为事件C.而
,
.
(2)零假设为:箱产量与养殖方法无关.
箱产量<50kg
旧养殖法 62 38
新养殖法 34 66
由计算可得:.
根据小概率值α=0.001的独立性检验,我们判断不成立.即认为箱产量与养殖方法有关.
(3),,
中位数为52.35.
20.答案:见解析
解析:依题意:.
故
,
,
则.
故管理时间y与土地使用面积x线性相关.
(2)依题意,计算得的值为:
.
根据小概率值α=0.001的独立性检验,我们判断不成立,即认为村民的性别与参与管理的意愿具有相关性.
21.答案:见解析
解析:(1)令,则可转化为,因为,所以
.
则,所以,
所以y关于x的经验回归方程为.
(2)y与的相关系数为:
,
因为,所以用反比例函数模型拟合效果更好,当x=10时,(元),所以当产量为10千件时,每件产品的非原料成本为21元;
(3)①当产品单价为100元时,设订单数为x千件.因为签订9千件订单的概率为0.8,签订10千件订单的概率为0.2,所以E(x)=9×0.8+10×0.3=9.2,所以企业利润为10100×9.2-9.2×(9.2
+21)=626.8(千元),
②当产品单价为90元,设订单数为y千件:因为签订10千件订单的概率为0.3,签订11千件订单的概率为0.7,所以E(y)=10×0.3+11×0.7=10.7,所以企业利润为(千元),故企业要想获得更高利润,产品单价应选择90元.
22.答案:见解析
解析:(1)散点图如下图.
,
.
计算得.
故所求经验回归方程为.
(2)列出残差表为.
0.05 0.005 -0.08 -0.045 0.04 0.025
-2.237 -1.367 -0.537 0.413 1.413 2.313
所以.
所以,回归模型的拟合效果较好.
(3)由残差表中的数值可以看出第3个样本点的残差比较大,需要确认在采集这个样本点的时候是否有人为的错误,如果有的话,需要纠正,重新建立回归模型;由表中数据可以看出残差点比较均匀地落在狭窄的水平带状区域中,说明选用的线性回归模型的精度较高,由以上分析可知,弹簧长度与所挂物体的质量成线性关系.
1 / 17
一、选择题
1.已知x,y是两个变量,下列四个关系中,x,y呈负相关的是( )
A.
B.
C.
D.
2.如果两个变量之间的线性相关程度很高,则其相关系数r的绝对值应接近于( )
A.0.5
B.2
C.0
D.1
3.两个变量的散点图如图,可考虑用如下函数进行拟合比较合理的是( )
A.
B.
C.
D.
4.一位母亲记录了儿子3~9岁的身高,数据(略),由此建立的身高与年龄的回归模型为,用这个模型预测这个孩子10岁时的身高,则正确的叙述是( )
A.身高一定是145.83cm
B.身高在145.83cm以上
C.身高在145.83cm左右
D.身高在145.83cm以下
5.在一组样本数据的散点图中,若所有样本点都在直线上,则这组样本数据的样本相关系数为( )
A.
B.0
C.
D.1
6.已知变量x与y正相关,且由观测数据算得样本平均数,则由该观测的数据算得的经验回归方程可能是( )
A.
B.
C.
D.
7.为了研究高中学生对乡村音乐的态度(喜欢和不喜欢两种态度)与性别的关系,运用2×2列联表进行独立性检验,经计算得=7.01,则认为“喜欢乡村音乐与性别有关系”的把握约为( )
A.0.1%
B.1%
C.99%
D.99.9%
8.某研究所为了检验某血清预防感冒的作用,把500名使用了该血清的志愿者与另外500名未使用该血清的志愿者一年中的感冒记录作比较,提出假设:“这种血清不能起到预防感冒的作用”,利用2×2列联表计算得≈3.918,经查临界值表知P(≥3.841)=0.05.则下列叙述中正确的是( )
A.有95%的把握认为“这种血清能起到预防感冒的作用”
B.若有人未使用该血清,那么他一年中有95%的可能性得感冒
C.这种血清预防感冒的有效率为95%
D.这种血清预防感冒的有效率为5%
9.在吸烟与患肺病这两个分类变量的计算中,下列说法正确的是( )
A.若>6.635,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病
B.从独立性检验可知,有99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有99%的可能患有肺病
C.若从统计量中得出有95%的把握认为吸烟与患肺病有关系,是指有5%的可能性使得推断出现错误
D.以上三种说法都不正确
10.根据如下样本数据
x 3 4 5 6 7 8
y 4.0 2.5 -0.5 0.5 -2.0 -3.0
得到的经验回归方程为,则( )
A.
B.
C.
D.
11.某化工厂为预测某产品的回收率y,需要研究它和原料有效成分含量x之间的相关关系,现取了8对观测值,计算得,则y与x的回归直线方程是( )
A.
B.
C.
D.
12.已知变量y关于x的经验回归方程为,其一组数据如下表所示.
x 1 2 3 4
y e
若x=5,则预测y的值可能为( )
A.
B.
C.
D.
二、填空题
13.以模型去拟合一组数据时,为了求出回归方程,设之,其变换后得到线性回归方程z=0.3x+4,则c=_________.
14.已知第一组样本点为(-5,-8.9),(-4,-7.2),(-3,-4.8),(-2,-3.3),(-1,-0.9),其变量间的相关系数为;第二组样本点为(1,8.9),(2,7.2),(3,4.8),(4,3.3),(5,0.9)其变量间的相关系数为.则,的大小关系为_________.
15.高三年级267位学生参加期末考试,某班37位学生的语文成绩,数学成绩与总成绩在全年级中的排名情况如下,甲、乙、丙为该班三位学生.
从这次考试成绩看:
(1)在甲、乙两人中,其语文成绩名次比其总成绩名次靠前的学生是_________.
(2)在语文和数学两个科目中,丙同学的成绩名次更靠前的科目是_________.
16.某班主任对全班50名学生作了一次调查,所得数据如表:
0.05 0.01
3.841 6.635
认为作业多 认为作业不多 总计
喜欢玩电脑游戏 18 9 27
不喜欢玩电脑游戏 8 15 23
总计 26 24 50
由表中数据计算得到≈5.059,于是___________(填“能”或“不能”)在犯错误的概率不超过0.01的前提下认为喜欢玩电脑游戏与认为作业多有关.
三、解答题
17.电视传媒公司为了解某地区电视观众对某体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图.
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性.
(1)根据已知条件完成下面2×2列联表,并据此资料和小概率值α=0.05的独立性检验是否认为“体育迷”与性别有关?
非体育迷 体育迷 合计
男
女
合计
(2)将日均收看该体育节目不低于50分钟的观众称为“超级体育迷”,已知“超级体育迷”中有2名女性.若从“超级体育迷”中任意选取2人,求至少有1名女性观众的概率.
附:.
0.050 0.010 0.001
3.841 6.635 10.825
18.(2018·全国卷Ⅲ改编)某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图.
(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;
(2)求40名工人完成生产任务所需时间的中位数m,并将完成生产任务所需时间超过m和不超过m的工人数填入下面的列联表:
超过m 不超过m
第一种生产方式
第二种生产方式
(3)根据(2)中的列联表,和小概率值α=0.1的独立性检验,是否认为两种生产方式的效率有差异?
附:
a 0.050 0.010 0.001
3.841 6.635 10.825
19.(2017·全国卷Ⅱ改编)海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取100个网箱,测量各箱水产品的产量(单位:kg),其频率分布直方图如下:
(1)设两种养殖方法的箱产量相互独立,记A表示事件“旧养殖法的箱产量低于50kg,新养殖法的箱产量不低于50kg”,估计A的概率;
(2)填写下面列联表,并根据小概率值α=0.01的独立性检验,是否认为箱产量与养殖方法有关.
箱产量<50kg
旧养殖法
新养殖法
(3)根据箱产量的频率分布直方图,求新养殖法箱产量的中位数的估计值(精确到0.01).
附:
0.050 0.010 0.001
3.841 6.635 10.828
.
20.(12分)近年来,国资委、党委高度重视扶贫开发工作,坚决贯彻落实中央扶贫工作重大决策部署,在各个贫困县全力推进定点扶贫各项工作,取得了积极成效,某贫困县为了响应国家精准扶贫的号召,特地承包了一块土地,已知土地的使用面积以及相应的管理时间的关系如下表所示:
土地使用面积x(单位:亩) 1 2 3 4 5
管理时间y(单位:月) 8 10 13 25 24
并调查了某村300名村民参与管理的意愿,得到的部分数据如下表所示:
愿意参与管理 不愿意参与管理
男性村民 150 50
女性村民 50
(1)求出相关系数r的大小,并判断管理时间y(月)与土地使用面积x(亩)是否线性相关?
(2)根据小概率值α=0.001的独立性检验,是否认为村民的性别与参与管理的意愿具有相关性?
参考公式:
.
临界值表:
0.100 0.050 0.025 0.010 0.001
2.706 3.841 5.024 6.635 10.828
参考数据:
21.某企业新研发了一种产品,产品的成本由原料成本及非原料成本组成.每件产品的非原料成本y(元)与生产该产品的数量x(千件)有关,经统计得到如下数据.
x 1 2 3 4 5 6 7 8
y 112 61 44.5 35 30.5 28 25 24
根据以上数据,绘制了散点图.
观察散点图,两个变量不具有线性相关关系,现考虑用反比例函数模型和指数函数模型分别对两个变量的关系进行拟合.已求得用指数函数模型拟合的回归方程为,lny与x的相关系数=-0.94.
(1)用反比例函数模型求y关于x的经验回归方程;
(2)用相关系数判断上述两个模型哪一个拟合效果更好(精确到0.01),并用其估计产量为10千件时每件产品的非原料成本;
(3)该企业采取订单生产模式(根据订单数量进行生产,即产品全部售出).根据市场调研数据,若该产品单价定为100元,则签订9千件订单的概率为0.8,签订10千件订单的概率为0.2;若单价定为90元,则签订10千件订单的概率为0.3,签订11千件订单的概率为0.7.已知每件产品的原料成本为10元,根据(2)的结果,企业要想获得更高利润,产品单价应选择100元还是90元,请说明理由.
参考数据(其中):
183.4 0.34 0.115 1.53 360 22385.5 61.4 0.135
参考公式:对于一组数据,其回归直线的斜率和截距的最小二乘估计分别为:,相关系数
22.为研究质量x(单位:g)对弹簧长度y(单位:cm)的影响,对不同质量的6个物体进行测量,数据如表所示.
x 5 10 15 20 25 30
y 7.25 8.12 8.95 9.90 10.9 11.8
(1)作出散点图并求经验回归方程;
(2)求出并说明回归模型拟合的程度;
(3)进行残差分析.
答案解析
一、选择题
1.答案:D
解析:根据题意,依次分析选项:对于A,,当x增大时,y的值不一定减小,两个变量不是负相关,不符合题意;对于B,,当x增大时,y的值不一定减小,两个变量不是负相关,不符合题意;对于C,,当x增大时,y的值一定增大,两个变量正相关,不符合题意;对于D,,当x增大时,y的值一定减小,两个变量负相关,符合题意.
2.答案:D
解析:相关系数越接近于1,相关程度越高.
3.答案:B
解析:本题考查学生数学抽象、数学建模的核心素养.由散点图可知,此曲线类似对数函数型曲线,因此可用函数模型进行拟合.
4.答案:C
解析:将x的值代入回归方程,可以预测孩子10岁时的身高为83.
5.答案:D
解析:因为所有的点都在直线上,这组样本数据完全正相关,故其相关系数为1.
6.答案:A
解析:因为变量与正相关,所以排除选项C,D,又因为回归直线必过样本中心点(3,3.5),代入检验知,只有直线过点(3,3.5)
7.答案:C
解析:易知=7.01>6.635,对照临界值表知,有99%的把握认为喜欢乡村音乐与性别有关系.
8.答案:A
解析:≈3.918>3.841,因此有95%的把握认为“这种血清能起到预防感冒的作用”..
9.答案:C
解析:A,B是对的误解,99%的把握认为吸烟和患肺病有关,是指通过大量的观察试验得出的一个数值,并不是100个人中必有99个人患肺病,也可能这100个人全健康.
10.答案:B
解析:依题意,画散点图知,两个变量负相关,所以b<0,a>0.
11.答案:A
解析:由题意知,,
则,
.
12.答案:D
解析:将式子两边取对数,得到,令,得到,列出x,z的取值对应的表格,
x 1 2 3 4
z 1 3 4 6
则,
,
解得,当x=5时,.
二、填空题
13.答案:
解析:,两边取对数.可得,
令z=lny,可得.
14.答案:>
解析:由第1组数据可知,两变量间成正相关,故>0,由第2组数据可知,两变量间成负相关,故<0,故>0>.
15.答案:乙;数学
解析:数学①由图可知,甲的语文成绩排名比总成绩排名靠后;而乙的语文成绩排名比总成绩排名靠前,故填乙.②由图可知,比丙的数学成绩排名还靠后的人比较多;而总成绩的排名中比丙排名靠后的人数比较少,所以丙的数学成绩的排名更靠前.
16.答案:不能
解析:查表知若要在犯错误的概率不超过0.01的前提下认为喜欢玩电脑游戏与认为作业多有关,则临界值=6.635.本题中,k≈5.059<6.635,所以不能在犯错误的概率不超过0.01的前提下认为喜欢玩电脑游戏与认为作业多有关.
三、解答题
17.答案:见解析
解析:(1)零假设为:“体育迷”与性别无关.由频率颁布直方图可知,在抽取的100人中,“体育迷”有25人,从而2×2列联表如下:
非体育迷 体育迷 合计
男 30 15 45
女 45 10 55
合计 75 25 100
由2×2列联表中数据代入公式计算,得:
=.
因为3.030<3.841,所以,根据小概率值α=0.05的独立检验,认为“体育迷”与性别有关.
(2)由频率分布直方图可知,“超级体育迷”为5人,从而一切可能结果所组成的基本事件空间
其中表示男生,
表示女生,j=1,2.由10个基本事件组成,而且这些事件的出现是等可能的.用A表示“任选2人中至少有1名是女性”这一事件,则A=
.
.
18.答案:见解析
解析:(1)第二种生产方式的效率更高.理由如下:
①由茎叶图可知:用第一种生产方式的工人中,有75%的工人完成生产任务所需时间至少80分钟,用第二种生产方式的工人中,有75%的工人完成生产任务所需时间至多79分钟.因此第二种生产方式的效率更高.
②由茎叶图可知:用第一种生产方式的工人完成生产任务所需时间的中位数为85.5分钟,用第二种生产方式的工人完成生产任务所需时间的中位数为73.5分钟.因此第二种生产方式的效率更高.
③由茎叶图可知:用第一种生产方式的工人完成生产任务平均所需时间高于80分钟;用第二种生产方式的工人完成生产任务平均所需时间低于80分钟,因此第二种生产方式的效率更高.
④由茎叶图可知:用第一种生产方式的工人完成生产任务所需时间分布在茎8上的最多,关于茎8大致呈对称分布;用第二种生产方式的工人完成生产任务所需时间分布在茎7上的最多,关于茎7大致呈对称分布,又用两种生产方式的工人完成生产任务所需时间分布的区间相同,故可以认为用第二种生产方式完成生产任务所需的时间比用第一种生产方式完成生产任务所需的时间更少,因此第二种生产方式的效率更高.
(2)由茎叶图知.列联表如下.
超过m 不超过m
第一种生产方式 15 5
第二种生产方式 5 15
(3)零假设:两种生产方式的效率没有差异.由于,所以根据小概率值α=0.1的独立性检验,判断不成立,即认为两种生产方式的效率有差异.
19.答案:见解析
解析:(1)记:“旧养殖法的箱产量低于50kg”为事件B,“新养殖法的箱产量不低于50kg”为事件C.而
,
.
(2)零假设为:箱产量与养殖方法无关.
箱产量<50kg
旧养殖法 62 38
新养殖法 34 66
由计算可得:.
根据小概率值α=0.001的独立性检验,我们判断不成立.即认为箱产量与养殖方法有关.
(3),,
中位数为52.35.
20.答案:见解析
解析:依题意:.
故
,
,
则.
故管理时间y与土地使用面积x线性相关.
(2)依题意,计算得的值为:
.
根据小概率值α=0.001的独立性检验,我们判断不成立,即认为村民的性别与参与管理的意愿具有相关性.
21.答案:见解析
解析:(1)令,则可转化为,因为,所以
.
则,所以,
所以y关于x的经验回归方程为.
(2)y与的相关系数为:
,
因为,所以用反比例函数模型拟合效果更好,当x=10时,(元),所以当产量为10千件时,每件产品的非原料成本为21元;
(3)①当产品单价为100元时,设订单数为x千件.因为签订9千件订单的概率为0.8,签订10千件订单的概率为0.2,所以E(x)=9×0.8+10×0.3=9.2,所以企业利润为10100×9.2-9.2×(9.2
+21)=626.8(千元),
②当产品单价为90元,设订单数为y千件:因为签订10千件订单的概率为0.3,签订11千件订单的概率为0.7,所以E(y)=10×0.3+11×0.7=10.7,所以企业利润为(千元),故企业要想获得更高利润,产品单价应选择90元.
22.答案:见解析
解析:(1)散点图如下图.
,
.
计算得.
故所求经验回归方程为.
(2)列出残差表为.
0.05 0.005 -0.08 -0.045 0.04 0.025
-2.237 -1.367 -0.537 0.413 1.413 2.313
所以.
所以,回归模型的拟合效果较好.
(3)由残差表中的数值可以看出第3个样本点的残差比较大,需要确认在采集这个样本点的时候是否有人为的错误,如果有的话,需要纠正,重新建立回归模型;由表中数据可以看出残差点比较均匀地落在狭窄的水平带状区域中,说明选用的线性回归模型的精度较高,由以上分析可知,弹簧长度与所挂物体的质量成线性关系.
1 / 17
