人教A版(2019)高中数学选择性必修第三册 《成对数据的统计分析》学业水平测试题(含答案)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第三册 《成对数据的统计分析》学业水平测试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 16:10:46 | ||
图片预览



文档简介
《成对数据的统计分析》学业水平测试题
一、选择题(本大题共5小题,每小题6分,共30分.在每小题给出的四个选项中,只有一项符合题目的要求.)
1.观察下列散点图,关于两个变量的相关关系推断正确的是( ).
(A)(1)为正相关,(2)为负相关,(3)为不相关
(B)(1)为负相关,(2)为不相关,(3)为正相关
(C)(1)为负相关,(2)为正相关,(3)为不相关
(D)(1)为正相关,(2)为不相关,(3)为负相关
2.对于样本相关系数,下列说法错误的是( ).
(A)样本相关系数可以用来判断成对样本数据相关的正负性
(B)样本相关系数可以是正的,也可以是负的
(C)样本相关系数越大,成对样本数据的线性相关程度也越强
(D)样本相关系数
3.由成对样本数据得到的经验回归方程为,则下列说法正确的是( ).
(A)直线必过点
(B)直线至少经过点中的一点
(C)直线是由中的两点确定的
(D)这个点到直线的距离之和最小
4.某人研究中学生的性别与成绩、视力、智商、阅读量这四个变量的关系,随机抽查52名中学生,得到如下4个列联表,则与性别有关联的可能性最大的变量是( ).
(A)成绩
(B)视力
(C)智商
(D)阅读量
5.通过随机询问某中学110名中学生是否爱好跳绳,得到如下列联表.
已知,根据小概率值的独立性检验,则以下结论正确的是( ).
(A)爱好跳绳与性别有关
(B)爱好跳绳与性别有关,这个结论犯错误的概率不超过0.001
(C)爱好跳绳与性别无关
(D)爱好跳绳与性别无关,这个结论犯错误的概率不超过
二、填空题(本题共3小题,每小题6分,共18分.将答案填在题中的横线上.)
6.已知成对样本数据中不全相等,且所有样本点都在直线上,则这组成对样本数据的样本相关系数_____.
7.以下4幅散点图所对应的样本相关系数的大小关系为_____.
(1)相关系数为 (2)相关系数为
(3)相关系数为 (4)相关系数为
8.已知变量之间具有线性相关关系,根据10对样本数据求得经验回归方程为.若,则_____.
三、解答题(本题共3小题,第9小题18分,第10小题18分,第11小题16分,共52分.解答应写出文字说明、证明过程或演算步骤.)
9.为研究鲈鱼体重与身长的关系,某鱼类研究所得到如下表所示的样本数据.
(1)请画出散点图,并求鲈鱼身长与体重之间的线性样本相关系数.
(2)建立一元线性回归模型,求出经验回归方程,并预测当鲈鱼身长时体重的平均值是多少?该模型对预报鲈鱼的体重有帮助吗
10.混凝土的抗压强度较容易测定,而抗剪强度不易测定,工程中希望建立一种能由推算的经验公式,下表列出了现有的9对数据.
请根据散点图选择三种不同形式的回归方程,并根据值选出最优模型.
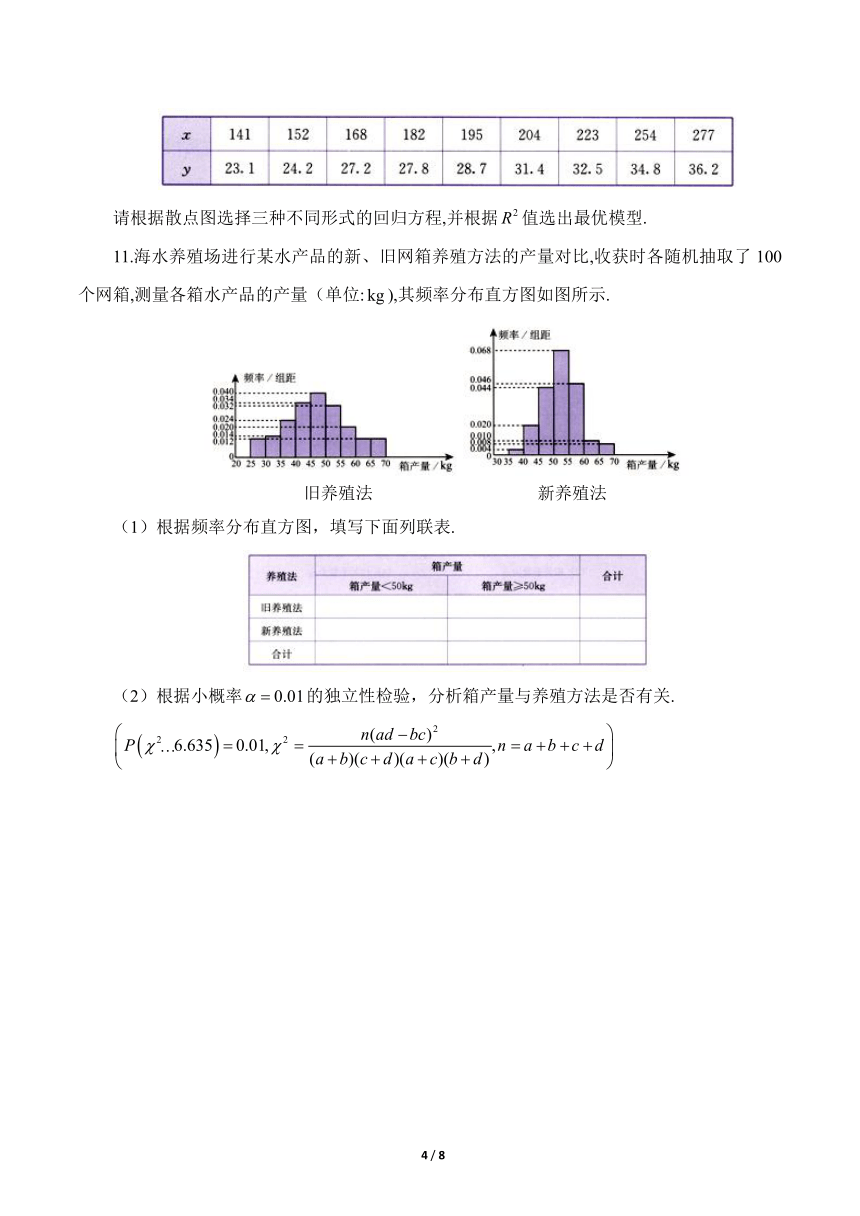
11.海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:),其频率分布直方图如图所示.
旧养殖法 新养殖法
(1)根据频率分布直方图,填写下面列联表.
(2)根据小概率的独立性检验,分析箱产量与养殖方法是否有关.
参考答案
1.D.本题评价学生对根据散点图直观推断两个变量相关性的了解程度,同时评价学生运用数形结合的思想进行数据分析的能力.
2.C.本题评价学生对样本相关系数统计含义的理解程度,同时评价学生运用概率与统计的方法进行推理论证的能力.
3.A.本题评价学生对回归直线性质和用最小二乘法估计一元线性回归模型参数的了解程度,同时评价学生运用概率与统计的思想进行推理论证的能力.
4.D.提示:可以根据频率的差异大小来直观推断两个分类变量是否有关联,也可以通过卡方独立性检验的方法.
本题通过列联表,评价学生对变量独立性的了解程度,同时评价学生运用概率与统计的思想进行数据分析的能力.
5.C.提示:计算可得,根据独立性检验规则,表明没有充分证据推断爱好跳绳与性别有关,可以认为爱好跳绳与性别无关.
6.1.本题通过散点的分布与样本相关系数的关系,评价学生对线性样本相关系数的几何意义的了解程度,同时评价学生运用数形结合的思想进行数据分析的能力.
7..本题通过样本相关系数的大小与散点分布之间的关系,评价学生对样本相关系数统计意义的了解程度,同时评价学生运用数形结合的思想进行数据分析的能力.
8.2.提示:因为,且点在回归直线3上,所以,得.
本题以经验回归直线的性质为载体,评价学生对一元线性回归模型的基本性质的了解程度,同时评价学生运用函数与方程的思想进行运算求解的能力.
9.(1)以鲈鱼的身长为横坐标、体重为纵坐标作散点图,如图(1)所示.在散点图中,散点大致分布在一条从左下角到右上角的直线附近,表明两个变量线性相关,并且是正相关,因此可以用线性回归模型刻画身长和体重之间的关系.
计算样本相关系数得
,
说明线性相关程度很高.
根据最小二乘法,利用统计软件计算,可得经验回归方程为,相应的经验回归直线如图(2)所示.
根据经验回归方程,可以计算鲈鱼体重的预测值及相应的残差,如下表所示.
以鲈鱼的身长为横坐标,残差为纵坐标,作残差图如图(3)所示.观察残差表和残差图可以看到,残差绝对值的最大值是,所有残差均匀地分布在以横轴为对称轴的带状区域内,可见经验回归方程可以较好地刻画鲈鱼体重与身长的关系.我们可以根据经验回归方程由身长预测体重.当时,,即当鲈鱼身长时,它体重的均值是.模型对于预报鲈鱼的体重是有帮助的.
本题通过建构一元线性回归模型解决实际问题,经历线性回归分析的全过程,评价学生对一元线性回归模型的掌握程度,同时评价学生运用概率与统计的思想进行数学建模的能力.
10.以抗压强度为横坐标,抗压强度为纵坐标作出散点图,如图(1)所示.
根据散点图,我们可以选择三种函数模型:
(1);(2);(3).
(1)如果认为散点是集中在直线附近,那么根据一元线性回归模型及最小二乘法,得到经验回归方程为.
(2)如果认为散点是集中在曲线附近,令,对变量作变换,将的样本数据转换成的数据,那么根据一元线性回归模型及最小二乘法,得到回归方程为2.,即.
(3)如果认为散点是集中在曲线附近,令,对变量作变换,将的样本数据转换成的数据,那么根据一元线性回归模型及最小二乘法,得到回归方程为,即.
画出上述三个经验回归方程的图象,如图(2)所示,并比较的大小.可以发现,以上三个回归方程都能较好地对样本数据进行拟合,其中第三个经验回归方程是最优模型.
本题通过散点图选择不同的函数模型作为回归曲线,综合评价学生对一元线性回归分析的掌握程度,同时评价学生运用数形结合的思想进行数学建模和数据分析的能力.
11.(1)旧养殖法箱产量小于的有62箱,所以旧养殖法箱产量不小于有的38箱;新养殖法箱产量小于的有箱,所以新养殖法箱产量不小于有的66箱.根据箱产量的频率分布直方图,得到如下列联表.
(2)零假设箱产量与养殖方法独立,即箱产量与养殖方法无关.根据列联表中的数据,经计算得到,根据小概率的独立性检验,我们推断不成立,即认为箱产量与养殖方法有关,此推断犯错误的概率不大于.
根据列联表中的数据计算,旧养殖法箱产量小于和不小于的频率分别为和;新养殖法箱产量小于和不小于的频率分别为和0.66.由,可见在随机抽取的样本中,新养殖法箱产量不小于的频率是旧养殖法的倍以上.根据频率稳定于概率的原理,我们可以认为新养殖法箱产量不小于的概率明显大于旧养殖法箱产量不小于的概率.
本题主要评价学生对列联表与独立性检验的掌握程度,同时评价学生运用概率与统计的思想和数形结合的思想进行数据分析的能力.
3 / 8
一、选择题(本大题共5小题,每小题6分,共30分.在每小题给出的四个选项中,只有一项符合题目的要求.)
1.观察下列散点图,关于两个变量的相关关系推断正确的是( ).
(A)(1)为正相关,(2)为负相关,(3)为不相关
(B)(1)为负相关,(2)为不相关,(3)为正相关
(C)(1)为负相关,(2)为正相关,(3)为不相关
(D)(1)为正相关,(2)为不相关,(3)为负相关
2.对于样本相关系数,下列说法错误的是( ).
(A)样本相关系数可以用来判断成对样本数据相关的正负性
(B)样本相关系数可以是正的,也可以是负的
(C)样本相关系数越大,成对样本数据的线性相关程度也越强
(D)样本相关系数
3.由成对样本数据得到的经验回归方程为,则下列说法正确的是( ).
(A)直线必过点
(B)直线至少经过点中的一点
(C)直线是由中的两点确定的
(D)这个点到直线的距离之和最小
4.某人研究中学生的性别与成绩、视力、智商、阅读量这四个变量的关系,随机抽查52名中学生,得到如下4个列联表,则与性别有关联的可能性最大的变量是( ).
(A)成绩
(B)视力
(C)智商
(D)阅读量
5.通过随机询问某中学110名中学生是否爱好跳绳,得到如下列联表.
已知,根据小概率值的独立性检验,则以下结论正确的是( ).
(A)爱好跳绳与性别有关
(B)爱好跳绳与性别有关,这个结论犯错误的概率不超过0.001
(C)爱好跳绳与性别无关
(D)爱好跳绳与性别无关,这个结论犯错误的概率不超过
二、填空题(本题共3小题,每小题6分,共18分.将答案填在题中的横线上.)
6.已知成对样本数据中不全相等,且所有样本点都在直线上,则这组成对样本数据的样本相关系数_____.
7.以下4幅散点图所对应的样本相关系数的大小关系为_____.
(1)相关系数为 (2)相关系数为
(3)相关系数为 (4)相关系数为
8.已知变量之间具有线性相关关系,根据10对样本数据求得经验回归方程为.若,则_____.
三、解答题(本题共3小题,第9小题18分,第10小题18分,第11小题16分,共52分.解答应写出文字说明、证明过程或演算步骤.)
9.为研究鲈鱼体重与身长的关系,某鱼类研究所得到如下表所示的样本数据.
(1)请画出散点图,并求鲈鱼身长与体重之间的线性样本相关系数.
(2)建立一元线性回归模型,求出经验回归方程,并预测当鲈鱼身长时体重的平均值是多少?该模型对预报鲈鱼的体重有帮助吗
10.混凝土的抗压强度较容易测定,而抗剪强度不易测定,工程中希望建立一种能由推算的经验公式,下表列出了现有的9对数据.
请根据散点图选择三种不同形式的回归方程,并根据值选出最优模型.
11.海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:),其频率分布直方图如图所示.
旧养殖法 新养殖法
(1)根据频率分布直方图,填写下面列联表.
(2)根据小概率的独立性检验,分析箱产量与养殖方法是否有关.
参考答案
1.D.本题评价学生对根据散点图直观推断两个变量相关性的了解程度,同时评价学生运用数形结合的思想进行数据分析的能力.
2.C.本题评价学生对样本相关系数统计含义的理解程度,同时评价学生运用概率与统计的方法进行推理论证的能力.
3.A.本题评价学生对回归直线性质和用最小二乘法估计一元线性回归模型参数的了解程度,同时评价学生运用概率与统计的思想进行推理论证的能力.
4.D.提示:可以根据频率的差异大小来直观推断两个分类变量是否有关联,也可以通过卡方独立性检验的方法.
本题通过列联表,评价学生对变量独立性的了解程度,同时评价学生运用概率与统计的思想进行数据分析的能力.
5.C.提示:计算可得,根据独立性检验规则,表明没有充分证据推断爱好跳绳与性别有关,可以认为爱好跳绳与性别无关.
6.1.本题通过散点的分布与样本相关系数的关系,评价学生对线性样本相关系数的几何意义的了解程度,同时评价学生运用数形结合的思想进行数据分析的能力.
7..本题通过样本相关系数的大小与散点分布之间的关系,评价学生对样本相关系数统计意义的了解程度,同时评价学生运用数形结合的思想进行数据分析的能力.
8.2.提示:因为,且点在回归直线3上,所以,得.
本题以经验回归直线的性质为载体,评价学生对一元线性回归模型的基本性质的了解程度,同时评价学生运用函数与方程的思想进行运算求解的能力.
9.(1)以鲈鱼的身长为横坐标、体重为纵坐标作散点图,如图(1)所示.在散点图中,散点大致分布在一条从左下角到右上角的直线附近,表明两个变量线性相关,并且是正相关,因此可以用线性回归模型刻画身长和体重之间的关系.
计算样本相关系数得
,
说明线性相关程度很高.
根据最小二乘法,利用统计软件计算,可得经验回归方程为,相应的经验回归直线如图(2)所示.
根据经验回归方程,可以计算鲈鱼体重的预测值及相应的残差,如下表所示.
以鲈鱼的身长为横坐标,残差为纵坐标,作残差图如图(3)所示.观察残差表和残差图可以看到,残差绝对值的最大值是,所有残差均匀地分布在以横轴为对称轴的带状区域内,可见经验回归方程可以较好地刻画鲈鱼体重与身长的关系.我们可以根据经验回归方程由身长预测体重.当时,,即当鲈鱼身长时,它体重的均值是.模型对于预报鲈鱼的体重是有帮助的.
本题通过建构一元线性回归模型解决实际问题,经历线性回归分析的全过程,评价学生对一元线性回归模型的掌握程度,同时评价学生运用概率与统计的思想进行数学建模的能力.
10.以抗压强度为横坐标,抗压强度为纵坐标作出散点图,如图(1)所示.
根据散点图,我们可以选择三种函数模型:
(1);(2);(3).
(1)如果认为散点是集中在直线附近,那么根据一元线性回归模型及最小二乘法,得到经验回归方程为.
(2)如果认为散点是集中在曲线附近,令,对变量作变换,将的样本数据转换成的数据,那么根据一元线性回归模型及最小二乘法,得到回归方程为2.,即.
(3)如果认为散点是集中在曲线附近,令,对变量作变换,将的样本数据转换成的数据,那么根据一元线性回归模型及最小二乘法,得到回归方程为,即.
画出上述三个经验回归方程的图象,如图(2)所示,并比较的大小.可以发现,以上三个回归方程都能较好地对样本数据进行拟合,其中第三个经验回归方程是最优模型.
本题通过散点图选择不同的函数模型作为回归曲线,综合评价学生对一元线性回归分析的掌握程度,同时评价学生运用数形结合的思想进行数学建模和数据分析的能力.
11.(1)旧养殖法箱产量小于的有62箱,所以旧养殖法箱产量不小于有的38箱;新养殖法箱产量小于的有箱,所以新养殖法箱产量不小于有的66箱.根据箱产量的频率分布直方图,得到如下列联表.
(2)零假设箱产量与养殖方法独立,即箱产量与养殖方法无关.根据列联表中的数据,经计算得到,根据小概率的独立性检验,我们推断不成立,即认为箱产量与养殖方法有关,此推断犯错误的概率不大于.
根据列联表中的数据计算,旧养殖法箱产量小于和不小于的频率分别为和;新养殖法箱产量小于和不小于的频率分别为和0.66.由,可见在随机抽取的样本中,新养殖法箱产量不小于的频率是旧养殖法的倍以上.根据频率稳定于概率的原理,我们可以认为新养殖法箱产量不小于的概率明显大于旧养殖法箱产量不小于的概率.
本题主要评价学生对列联表与独立性检验的掌握程度,同时评价学生运用概率与统计的思想和数形结合的思想进行数据分析的能力.
3 / 8
