人教版九年级数学上册25.3用频率估计概率 导学练(附答案)
文档属性
| 名称 | 人教版九年级数学上册25.3用频率估计概率 导学练(附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 119.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 00:00:00 | ||
图片预览

文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
人教版九年级数学上册用频率估计概率导学练(附答案)
一、单选题
1.已知抛一枚均匀硬币正面朝上的概率为, 下列说法正确的是( ).
A. 连续抛一枚均匀硬币2次必有1次正面朝上
B. 连续抛一枚均匀硬币10次,不可能正面都朝上
C. 大量反复抛一枚均匀硬币,平均每100次出现正面朝上50次
D. 通过抛一枚均匀硬币确定谁先发球的比赛规则是公平的
2.某林业局将一种树苗移植成活的情况绘制成如统计图,由此可估计这种树苗移植成活的概率约为( )
A. 0.95 B. 0.90 C. 0.85 D. 0.80
3.下面关于投针实验的说法正确的是( )
A. 针与平行线相交和不相交的可能性是相同的
B. 针与平行线相交的概率与针的长度没有关系
C. 实验次数越多,估算针与平行线相交的概率越精确
D. 针与平行线相交的概率受两平行线间距离的影响
4.在同样的条件下对某种小麦种子进行发芽试验,统计发芽种子数,获得如下频数表,由表估计该麦种的发芽概率是( )
试验种子数n(粒) 50 200 500 1000 3000
发芽频数m 45 188 476 951 2850
发芽频率 0.9 0.94 0.952 0.951 0.95
A. 0.8 B. 0.9 C. 0.95 D. 1
5.在同样的条件下对某种小麦种子进行发芽试验,统计发芽种子数,获得如下频数表,由表估计该麦种的发芽概率是( )
试验种子数n(粒) 50 200 500 1000 3000
发芽频数m 45 188 476 951 2850
发芽频率 0.9 0.94 0.952 0.951 0.95
A. 0.8 B. 0.9 C. 0.95 D. 1
二、填空题
6.在一个不透明的布袋中装有红色、白色玻璃球共40个,除颜色外其他安全相同,小明通过多次摸球试验后发现,其中摸到红色球的频率稳定在0.15左右,则口袋中红色球可能有________个.
7.某射击运动员在相同条件下的射击160次,其成绩记录如下:
射击次数 20 40 60 80 100 120 140 160
射中9环以上的次数 15 33 48 63 79 97 111 130
射中9环以上的频率 0.75 0.83 0.80 0.79 0.79 0.81 0.79 0.81
根据频率的稳定性,估计这名运动员射击一次时“射中9环以上”的概率 ________(精确到0.1).
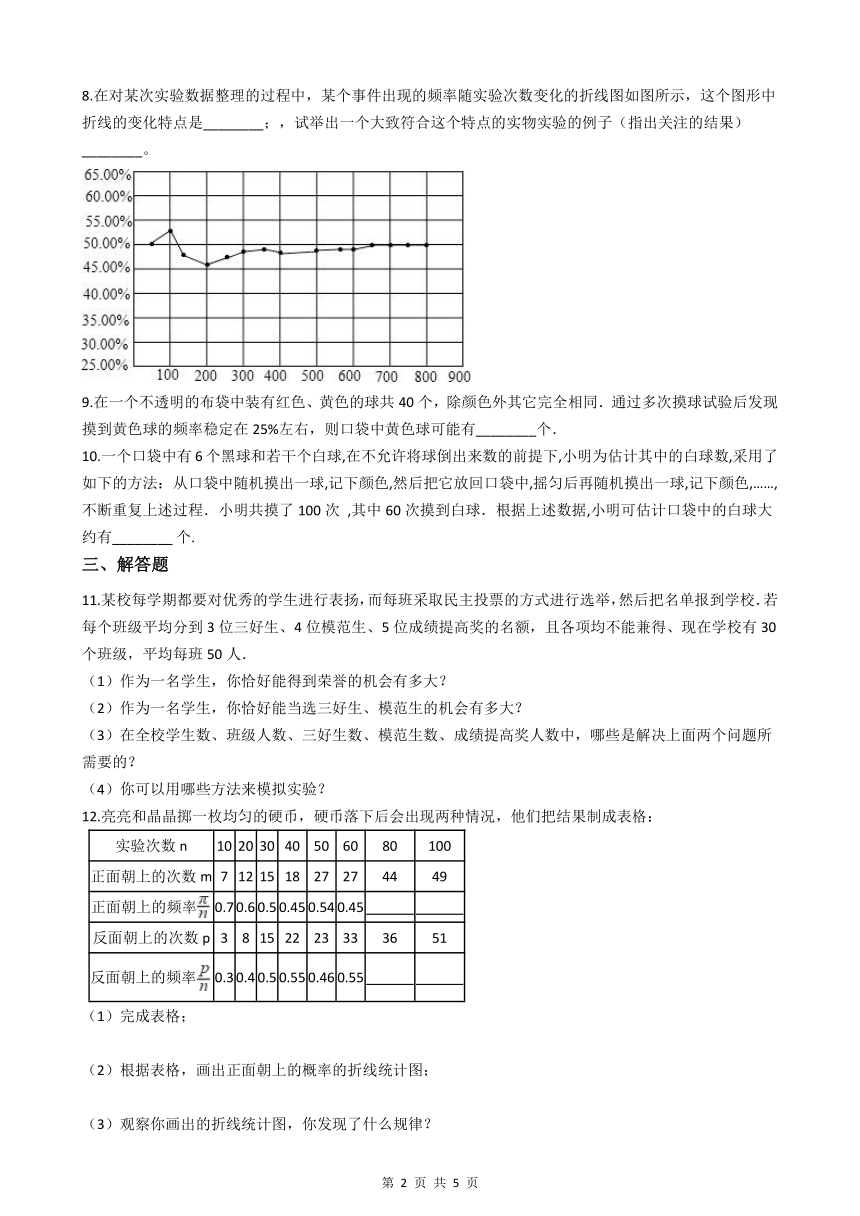
8.在对某次实验数据整理的过程中,某个事件出现的频率随实验次数变化的折线图如图所示,这个图形中折线的变化特点是________;,试举出一个大致符合这个特点的实物实验的例子(指出关注的结果)________。
9.在一个不透明的布袋中装有红色、黄色的球共40个,除颜色外其它完全相同.通过多次摸球试验后发现摸到黄色球的频率稳定在25%左右,则口袋中黄色球可能有________个.
10.一个口袋中有6个黑球和若干个白球,在不允许将球倒出来数的前提下,小明为估计其中的白球数,采用了如下的方法:从口袋中随机摸出一球,记下颜色,然后把它放回口袋中,摇匀后再随机摸出一球,记下颜色,……,不断重复上述过程.小明共摸了100次 ,其中60次摸到白球.根据上述数据,小明可估计口袋中的白球大约有________ 个.
三、解答题
11.某校每学期都要对优秀的学生进行表扬,而每班采取民主投票的方式进行选举,然后把名单报到学校.若每个班级平均分到3位三好生、4位模范生、5位成绩提高奖的名额,且各项均不能兼得、现在学校有30个班级,平均每班50人.
(1)作为一名学生,你恰好能得到荣誉的机会有多大?
(2)作为一名学生,你恰好能当选三好生、模范生的机会有多大?
(3)在全校学生数、班级人数、三好生数、模范生数、成绩提高奖人数中,哪些是解决上面两个问题所需要的?
(4)你可以用哪些方法来模拟实验?
12.亮亮和晶晶掷一枚均匀的硬币,硬币落下后会出现两种情况,他们把结果制成表格:
实验次数n 10 20 30 40 50 60 80 100
正面朝上的次数m 7 12 15 18 27 27 44 49
正面朝上的频率 0.7 0.6 0.5 0.45 0.54 0.45
反面朝上的次数p 3 8 15 22 23 33 36 51
反面朝上的频率 0.3 0.4 0.5 0.55 0.46 0.55
(1)完成表格;
(2)根据表格,画出正面朝上的概率的折线统计图;
(3)观察你画出的折线统计图,你发现了什么规律?
13.一只不透明的袋子中装有 个质地、大小均相同的小球,这些小球分别标有数字 ,甲、乙两人每次同时从袋中各随机摸出 个球,并计算摸出的这 个小球上数字之和,记录后都将小球放回袋中搅匀,进行重复实验.实验数据如下表
摸球总次数 10 20 30 60 90 120 180 240 330 450
“和为 ”出现的频数 2 10 13 24 30 37 58 82 110 150
“和为 ”出现的频率 0.20 0.50 0.43 0.40 0.363 0.31 0.32 0.34 0.33 0.33
解答下列问题:
(1)如果实验继续进行下去,根据上表数据,出现“和为8”的频率将稳定在它的概率附近.估计出现“和为8”的概率是________;
(2)如果摸出的这两个小球上数字之和为 的概率是 ,那么 的值可以取 吗?请用列表法或画树状图法说明理由;如果 的值不可以取 ,请写出一个符合要求的 值.
14.在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
摸球的次数n 100 200 300 500 800 1000 3000
摸到白球的次数m 65 124 178 302 481 599 1803
摸到白球的频率 0.65 0.62 0.593 0.604 0.601 0.599 0.601
(1)请估计:当n很大时,摸到白球的频率将会接近________;(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P(白球)=________;
(3)试估算盒子里黑、白两种颜色的球各有多少只?
答 案
一、单选题
1. D 2. B 3. C 4. C 5. C
二、填空题
6. 6 7. 0.8
8. 随着实验次数增加,频率趋于稳定于50%;抛掷一枚硬币实验中关注正面出现的频率
9. 10 10. 9
三、解答题
11. 解:(1)全班共有50名学生,共有12名学生获奖,所以恰好能得到荣誉的机会为=;
(2)恰好能当选三好生的机会为, 能当选模范生的机会为=;
(3)班级人数、三好生数、模范生数、成绩提高奖人数;
(4)用50个小球,其中3个红球、4个白球、5个黑球,其余均为黄球,把它们装进不透明的口袋中搅均,闭着眼从中摸出一个球,则摸到非黄球的机会就是得到荣誉的机会,摸到红球或白球的机会就是当选为三好生和模范生的机会.
12. 解:(1)
实验次数n 10 20 30 40 50 60 80 100
正面朝上的次数m 7 12 15 18 27 27 44 49
正面朝上的频率 0.7 0.6 0.5 0.45 0.54 0.45 0.55 0.49
反面朝上的次数p 3 8 15 22 23 33 36 51
反面朝上的频率 0.3 0.4 0.5 0.55 0.46 0.55 0.45 0.51
(2)折线统计图为:
(3)随着实验次数的增多,正面朝上的频率逐渐稳定到0.5左右.
13. (1)0.33
(2)解:当x=7时
3 4 5 7
3 7 8 10
4 7 9 11
5 8 9 12
7 10 11 12
则两个小球上数家之和为9的概率是
故x的值不可以取7.
∴出现和为9的概率是三分之一,即有3种可能,
∴3+x=9或4+x=9或5+x=9,
解得:x=6,x=5,x=4,故x的值可以为4,5,6其中一个.
14. (1)0.6(2)0.6(3)白球有24只,黑球有16只.
(
第
- 1 -
页 共
5
页
)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
人教版九年级数学上册用频率估计概率导学练(附答案)
一、单选题
1.已知抛一枚均匀硬币正面朝上的概率为, 下列说法正确的是( ).
A. 连续抛一枚均匀硬币2次必有1次正面朝上
B. 连续抛一枚均匀硬币10次,不可能正面都朝上
C. 大量反复抛一枚均匀硬币,平均每100次出现正面朝上50次
D. 通过抛一枚均匀硬币确定谁先发球的比赛规则是公平的
2.某林业局将一种树苗移植成活的情况绘制成如统计图,由此可估计这种树苗移植成活的概率约为( )
A. 0.95 B. 0.90 C. 0.85 D. 0.80
3.下面关于投针实验的说法正确的是( )
A. 针与平行线相交和不相交的可能性是相同的
B. 针与平行线相交的概率与针的长度没有关系
C. 实验次数越多,估算针与平行线相交的概率越精确
D. 针与平行线相交的概率受两平行线间距离的影响
4.在同样的条件下对某种小麦种子进行发芽试验,统计发芽种子数,获得如下频数表,由表估计该麦种的发芽概率是( )
试验种子数n(粒) 50 200 500 1000 3000
发芽频数m 45 188 476 951 2850
发芽频率 0.9 0.94 0.952 0.951 0.95
A. 0.8 B. 0.9 C. 0.95 D. 1
5.在同样的条件下对某种小麦种子进行发芽试验,统计发芽种子数,获得如下频数表,由表估计该麦种的发芽概率是( )
试验种子数n(粒) 50 200 500 1000 3000
发芽频数m 45 188 476 951 2850
发芽频率 0.9 0.94 0.952 0.951 0.95
A. 0.8 B. 0.9 C. 0.95 D. 1
二、填空题
6.在一个不透明的布袋中装有红色、白色玻璃球共40个,除颜色外其他安全相同,小明通过多次摸球试验后发现,其中摸到红色球的频率稳定在0.15左右,则口袋中红色球可能有________个.
7.某射击运动员在相同条件下的射击160次,其成绩记录如下:
射击次数 20 40 60 80 100 120 140 160
射中9环以上的次数 15 33 48 63 79 97 111 130
射中9环以上的频率 0.75 0.83 0.80 0.79 0.79 0.81 0.79 0.81
根据频率的稳定性,估计这名运动员射击一次时“射中9环以上”的概率 ________(精确到0.1).
8.在对某次实验数据整理的过程中,某个事件出现的频率随实验次数变化的折线图如图所示,这个图形中折线的变化特点是________;,试举出一个大致符合这个特点的实物实验的例子(指出关注的结果)________。
9.在一个不透明的布袋中装有红色、黄色的球共40个,除颜色外其它完全相同.通过多次摸球试验后发现摸到黄色球的频率稳定在25%左右,则口袋中黄色球可能有________个.
10.一个口袋中有6个黑球和若干个白球,在不允许将球倒出来数的前提下,小明为估计其中的白球数,采用了如下的方法:从口袋中随机摸出一球,记下颜色,然后把它放回口袋中,摇匀后再随机摸出一球,记下颜色,……,不断重复上述过程.小明共摸了100次 ,其中60次摸到白球.根据上述数据,小明可估计口袋中的白球大约有________ 个.
三、解答题
11.某校每学期都要对优秀的学生进行表扬,而每班采取民主投票的方式进行选举,然后把名单报到学校.若每个班级平均分到3位三好生、4位模范生、5位成绩提高奖的名额,且各项均不能兼得、现在学校有30个班级,平均每班50人.
(1)作为一名学生,你恰好能得到荣誉的机会有多大?
(2)作为一名学生,你恰好能当选三好生、模范生的机会有多大?
(3)在全校学生数、班级人数、三好生数、模范生数、成绩提高奖人数中,哪些是解决上面两个问题所需要的?
(4)你可以用哪些方法来模拟实验?
12.亮亮和晶晶掷一枚均匀的硬币,硬币落下后会出现两种情况,他们把结果制成表格:
实验次数n 10 20 30 40 50 60 80 100
正面朝上的次数m 7 12 15 18 27 27 44 49
正面朝上的频率 0.7 0.6 0.5 0.45 0.54 0.45
反面朝上的次数p 3 8 15 22 23 33 36 51
反面朝上的频率 0.3 0.4 0.5 0.55 0.46 0.55
(1)完成表格;
(2)根据表格,画出正面朝上的概率的折线统计图;
(3)观察你画出的折线统计图,你发现了什么规律?
13.一只不透明的袋子中装有 个质地、大小均相同的小球,这些小球分别标有数字 ,甲、乙两人每次同时从袋中各随机摸出 个球,并计算摸出的这 个小球上数字之和,记录后都将小球放回袋中搅匀,进行重复实验.实验数据如下表
摸球总次数 10 20 30 60 90 120 180 240 330 450
“和为 ”出现的频数 2 10 13 24 30 37 58 82 110 150
“和为 ”出现的频率 0.20 0.50 0.43 0.40 0.363 0.31 0.32 0.34 0.33 0.33
解答下列问题:
(1)如果实验继续进行下去,根据上表数据,出现“和为8”的频率将稳定在它的概率附近.估计出现“和为8”的概率是________;
(2)如果摸出的这两个小球上数字之和为 的概率是 ,那么 的值可以取 吗?请用列表法或画树状图法说明理由;如果 的值不可以取 ,请写出一个符合要求的 值.
14.在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
摸球的次数n 100 200 300 500 800 1000 3000
摸到白球的次数m 65 124 178 302 481 599 1803
摸到白球的频率 0.65 0.62 0.593 0.604 0.601 0.599 0.601
(1)请估计:当n很大时,摸到白球的频率将会接近________;(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P(白球)=________;
(3)试估算盒子里黑、白两种颜色的球各有多少只?
答 案
一、单选题
1. D 2. B 3. C 4. C 5. C
二、填空题
6. 6 7. 0.8
8. 随着实验次数增加,频率趋于稳定于50%;抛掷一枚硬币实验中关注正面出现的频率
9. 10 10. 9
三、解答题
11. 解:(1)全班共有50名学生,共有12名学生获奖,所以恰好能得到荣誉的机会为=;
(2)恰好能当选三好生的机会为, 能当选模范生的机会为=;
(3)班级人数、三好生数、模范生数、成绩提高奖人数;
(4)用50个小球,其中3个红球、4个白球、5个黑球,其余均为黄球,把它们装进不透明的口袋中搅均,闭着眼从中摸出一个球,则摸到非黄球的机会就是得到荣誉的机会,摸到红球或白球的机会就是当选为三好生和模范生的机会.
12. 解:(1)
实验次数n 10 20 30 40 50 60 80 100
正面朝上的次数m 7 12 15 18 27 27 44 49
正面朝上的频率 0.7 0.6 0.5 0.45 0.54 0.45 0.55 0.49
反面朝上的次数p 3 8 15 22 23 33 36 51
反面朝上的频率 0.3 0.4 0.5 0.55 0.46 0.55 0.45 0.51
(2)折线统计图为:
(3)随着实验次数的增多,正面朝上的频率逐渐稳定到0.5左右.
13. (1)0.33
(2)解:当x=7时
3 4 5 7
3 7 8 10
4 7 9 11
5 8 9 12
7 10 11 12
则两个小球上数家之和为9的概率是
故x的值不可以取7.
∴出现和为9的概率是三分之一,即有3种可能,
∴3+x=9或4+x=9或5+x=9,
解得:x=6,x=5,x=4,故x的值可以为4,5,6其中一个.
14. (1)0.6(2)0.6(3)白球有24只,黑球有16只.
(
第
- 1 -
页 共
5
页
)
同课章节目录
