人教版数学七年级上册2.2整式的加减(一) 同类项 课件(共20张PPT)
文档属性
| 名称 | 人教版数学七年级上册2.2整式的加减(一) 同类项 课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 19:38:33 | ||
图片预览







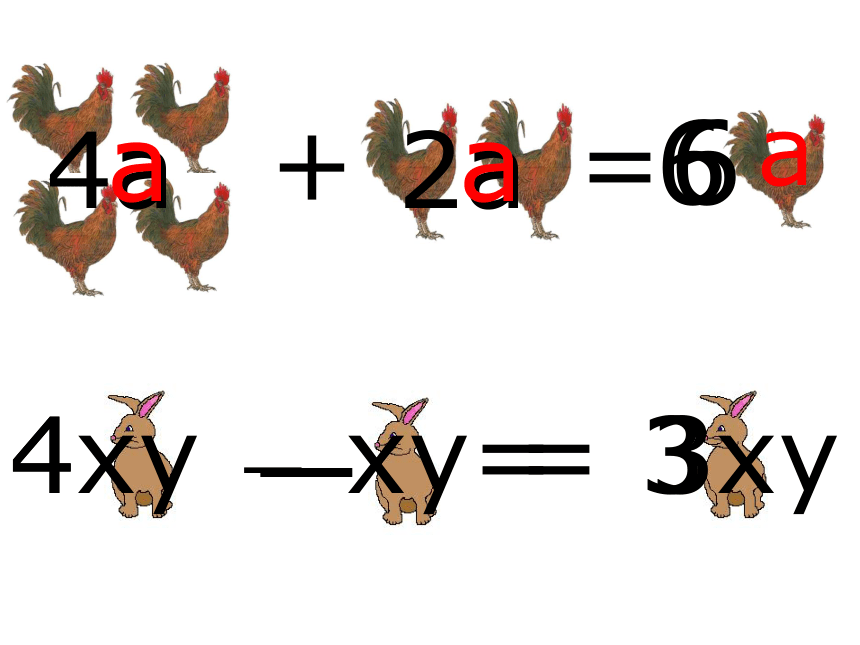
文档简介
(共21张PPT)
超市里新到的水果上架时怎样摆放呢?
问题2:
(1)在日常生活中,你发现还有哪些事物也需要分类?能举出例子吗?
(2)生活中处处有分类的问题,在数学中
也有分类的问题吗?
探讨:
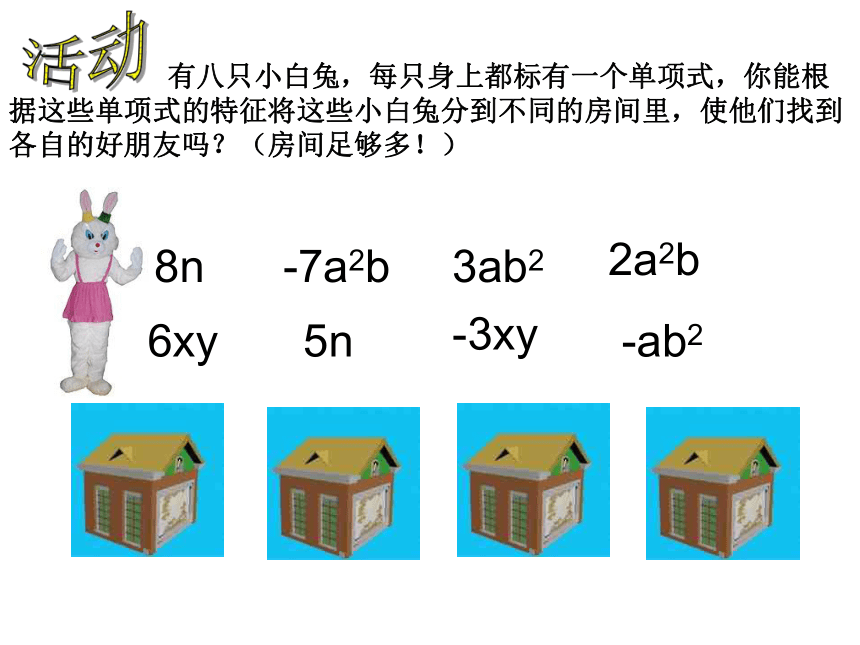
有八只小白兔,每只身上都标有一个单项式,你能根据这些单项式的特征将这些小白兔分到不同的房间里,使他们找到各自的好朋友吗?(房间足够多!)
8n
-7a2b
3ab2
2a2b
6xy
5n
-3xy
-ab2
8n 5n
3ab2 -ab2
6xy -3xy
-7a2b 2a2b
n
n
xy
xy
a b
a b
ab
ab
2
2
2
2
1、所含字母有何特点?
2、相同字母指数有何特点?
探究新知:
1、同类项的概念:
概念:所含字母相同,并且相同字母的指数也相同的项,叫做同类项。
注意:
(1) 同类项与系数无关,
与字母的排列顺序也无关
(2)几个常数项也是同类项。
下列各组中的两项是不是同类项?
(1)、 是同类项。
(2)、 是同类项。
(3)、 是同类项。
(4)、 是同类项。
(5)、 是同类项。
规则:一学生说出一个单项式后,指定一位同学回答它的两个同类项。
要求出题同学尽可能使自己的题目与众不同。
2:游戏
4
+ =
6
―
= 3
4a 2a
6
4xy ― xy=
3xy
a
a
a
每本练习本x元,小明买5本,小刚买2本,两人
一共花了多少钱?小明比小刚多花了多少钱?
小明用了______元
小刚用了______元
小明与小刚一共用了_____________元
5x
2x
5x + 2x
小明比小刚多花了________________元
5x - 2x
5x+2x=(5+2)x=7x
5x+2x=(5+2)x=7x
利用分配律, 可以知道小明与小刚买练习本一共用了7x元,小明比小刚多花了3x元。
思 考
我们把多项式的同类项合并成一项,叫做合并同类项
定义
合并同类项法则:
合并同类项后,所得项的系数是合并
前各同类项的系数的和,且字母部分不变。
注意:
合并的前提是有同类项.
合并指的是系数相加,”相加”指的是代数和.
合并同类项的根据是加法交换律、结合
律以及乘法分配律。
试一试.
合并下列各式的同类项:
(1)3x3+x3; (2)xy2- xy2。
解:(1)3x3+x3
=(3+1)x3
=4x3
(2)xy2- xy2
=(1- )xy2
= xy2
=( )+( )
(1) 6xy-10x2-5yx+7x2 +5x
合并同类项
(找)
6xy-5yx
-10x2+7x2
(移)
= xy
(6-5)
+ x2
(-10+7)
(并)
=xy-3x2
+5x
+5x
+5x
(1) 3x-8x-9x
(2) 5a2+2ab-4a2-4ab
(3) 2x-7y-5x+3+11y-1
=-14x
=a2-2ab
=-3x+4y+2
知 识 延 伸:
已知: 与
是同类项,求 m、n的值 .
2
_
3
x3my3
-
1
_
4
x6yn+1
∴ 3m=6 , n+1=3
∴ m=2 , n=2
解:
∵ 与
是同类项
2
_
3
x3my3
-
1
_
4
x6yn+1
通过这节课的学习:
我学会了……
使我感触最深的是……
我发现生活中……
必做作业:
P66练习:1,2,3 P71习题2.2:1题
课后提高练习:(选做题)
填空:
1.如果2a2 bn+1与-4amb3是同类项,则
m=____,n=____;
2.若5xy2+axy2=-2xy2,则a=___;
3.在6xy-3x2-4x2y-5yx2+x2中没有同类项
的项是______;
再见
超市里新到的水果上架时怎样摆放呢?
问题2:
(1)在日常生活中,你发现还有哪些事物也需要分类?能举出例子吗?
(2)生活中处处有分类的问题,在数学中
也有分类的问题吗?
探讨:
有八只小白兔,每只身上都标有一个单项式,你能根据这些单项式的特征将这些小白兔分到不同的房间里,使他们找到各自的好朋友吗?(房间足够多!)
8n
-7a2b
3ab2
2a2b
6xy
5n
-3xy
-ab2
8n 5n
3ab2 -ab2
6xy -3xy
-7a2b 2a2b
n
n
xy
xy
a b
a b
ab
ab
2
2
2
2
1、所含字母有何特点?
2、相同字母指数有何特点?
探究新知:
1、同类项的概念:
概念:所含字母相同,并且相同字母的指数也相同的项,叫做同类项。
注意:
(1) 同类项与系数无关,
与字母的排列顺序也无关
(2)几个常数项也是同类项。
下列各组中的两项是不是同类项?
(1)、 是同类项。
(2)、 是同类项。
(3)、 是同类项。
(4)、 是同类项。
(5)、 是同类项。
规则:一学生说出一个单项式后,指定一位同学回答它的两个同类项。
要求出题同学尽可能使自己的题目与众不同。
2:游戏
4
+ =
6
―
= 3
4a 2a
6
4xy ― xy=
3xy
a
a
a
每本练习本x元,小明买5本,小刚买2本,两人
一共花了多少钱?小明比小刚多花了多少钱?
小明用了______元
小刚用了______元
小明与小刚一共用了_____________元
5x
2x
5x + 2x
小明比小刚多花了________________元
5x - 2x
5x+2x=(5+2)x=7x
5x+2x=(5+2)x=7x
利用分配律, 可以知道小明与小刚买练习本一共用了7x元,小明比小刚多花了3x元。
思 考
我们把多项式的同类项合并成一项,叫做合并同类项
定义
合并同类项法则:
合并同类项后,所得项的系数是合并
前各同类项的系数的和,且字母部分不变。
注意:
合并的前提是有同类项.
合并指的是系数相加,”相加”指的是代数和.
合并同类项的根据是加法交换律、结合
律以及乘法分配律。
试一试.
合并下列各式的同类项:
(1)3x3+x3; (2)xy2- xy2。
解:(1)3x3+x3
=(3+1)x3
=4x3
(2)xy2- xy2
=(1- )xy2
= xy2
=( )+( )
(1) 6xy-10x2-5yx+7x2 +5x
合并同类项
(找)
6xy-5yx
-10x2+7x2
(移)
= xy
(6-5)
+ x2
(-10+7)
(并)
=xy-3x2
+5x
+5x
+5x
(1) 3x-8x-9x
(2) 5a2+2ab-4a2-4ab
(3) 2x-7y-5x+3+11y-1
=-14x
=a2-2ab
=-3x+4y+2
知 识 延 伸:
已知: 与
是同类项,求 m、n的值 .
2
_
3
x3my3
-
1
_
4
x6yn+1
∴ 3m=6 , n+1=3
∴ m=2 , n=2
解:
∵ 与
是同类项
2
_
3
x3my3
-
1
_
4
x6yn+1
通过这节课的学习:
我学会了……
使我感触最深的是……
我发现生活中……
必做作业:
P66练习:1,2,3 P71习题2.2:1题
课后提高练习:(选做题)
填空:
1.如果2a2 bn+1与-4amb3是同类项,则
m=____,n=____;
2.若5xy2+axy2=-2xy2,则a=___;
3.在6xy-3x2-4x2y-5yx2+x2中没有同类项
的项是______;
再见
