人教B版(2019)高中数学选择性必修第一册 1.1 .2《空间向量的数量积》教学设计
文档属性
| 名称 | 人教B版(2019)高中数学选择性必修第一册 1.1 .2《空间向量的数量积》教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 743.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 00:00:00 | ||
图片预览


文档简介
《空间向量的数量积》教学设计
一、问题引入,提出概念
前面我们刚刚学习了空间向量的加减法、数乘运算,通过学习发现这些运算与平面向量的加减法、数乘运算是完全一致的.我们还学面向量的数量积运算,从定义、几何意义、运算性质等方面认识了数量积运算,那么空间向量的数量积运算是怎样的呢?
设计意图:通过回顾空间向量的加减法、数乘运算的学习经验,让学生体会空间向量与平面向量的内在联系,暗示学生可运用类比的方法学习空间向量的数量积运算.借此,提出“空间向量的数量积”的概念,为后续自主探究、交流分享环节作好铺垫.
二、自主探究,交流分享
1.小组合作,自主探究.
分组:4人一组,每组确定1名组长,组长负责组织讨论、记录,汇报讨论结果.
引导:呈现研究平面向量数量积运算的几个维度,暗示学生探究的方向.
向量的数量积
平面向量 空间向量
向量夹 角的 定义、范围 平面内,给定两个非零向量,,任意在平面内选定一点,作,则大小在内的称为与的夹角,记作.
向量 垂直 如果 ,则称向量与垂直,记作.约定零向量与任意向量都垂直.
数量积定义 平面内,两个非零向量与的数量积(或内积)定义为.规定零向量与任意向量的数量积为0.
向量的数量积
平面向量 空间向量
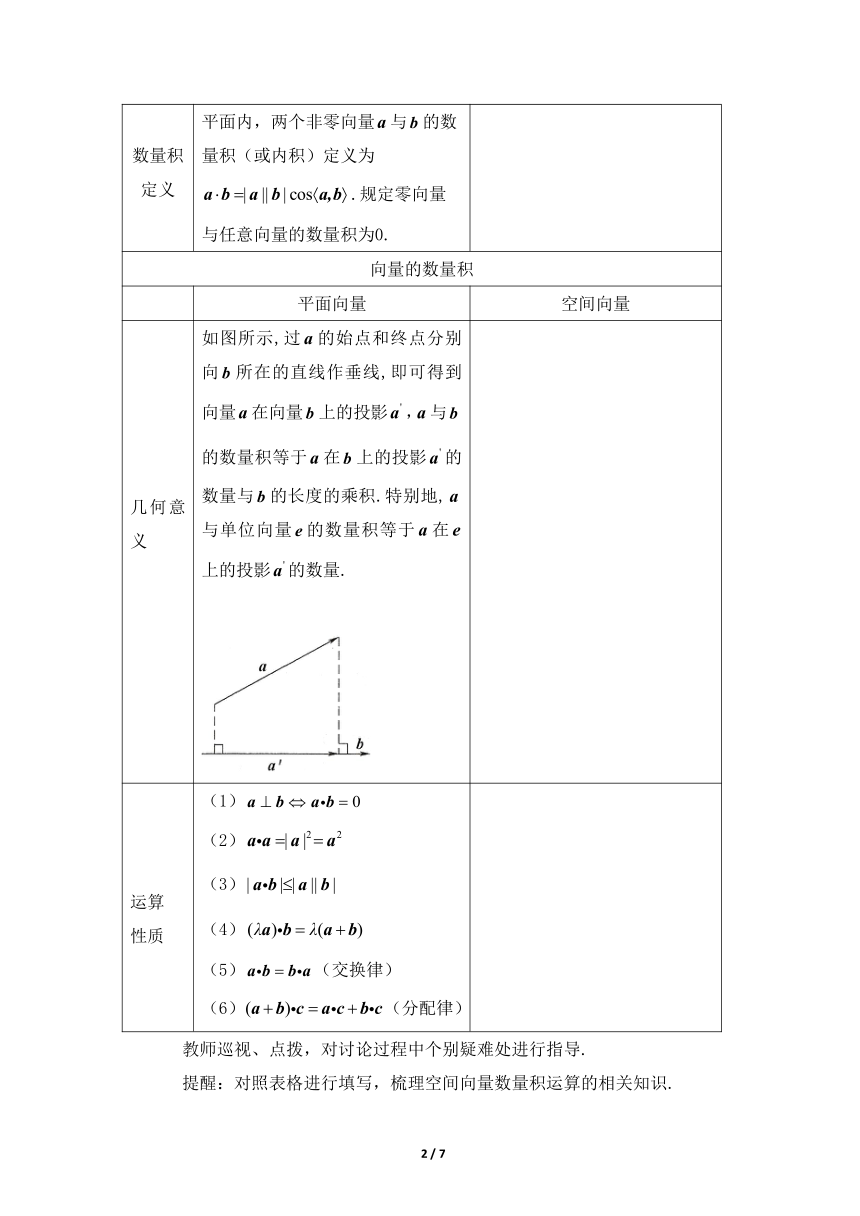
几何意义 如图所示,过的始点和终点分别向所在的直线作垂线,即可得到向量在向量上的投影,与的数量积等于在上的投影的数量与的长度的乘积.特别地,与单位向量的数量积等于在上的投影的数量.
运算 性质 (1) (2) (3) (4) (5)(交换律) (6)(分配律)
教师巡视、点拨,对讨论过程中个别疑难处进行指导.
提醒:对照表格进行填写,梳理空间向量数量积运算的相关知识.
设计意图:充分发挥学生的主体作用,凸显“以学生为主体的教,在教师引导下的学”的授课模式,让学生“动起来”,让课堂“活起来”.
2.概念辨析,交流分享.
(1)空间向量的夹角.
例1 如图所示是一个正方体,求下列各对向量的夹角:
(1)与;(2)与;(3)与
(4)与.
解(1)由于与的方向相同,所以==45°.
(2)==135°.
(3)==90°.
(4)==180°.
设计意图:通过具体实例的分析讲解,巩固空间向量夹角的概念.
(2)空间向量的投影.
空间向量在向量上的投影,除了按照平面向量的投影的方式得到之外,还可以过的始点和终点分别作与所在直线垂直的平面得到,这可以从下图所示的长方体中看出来,其中向量在棱上,=,因为=,,所以在向量上的投影=.
一般地,给定空间向量和空间中的直线(或平面),过的始点和终点分别作直线(或平面)的垂线,假设垂足为,,则向量称为在直线(或平面)上的投影.
设计意图:学生通过类比平面向量中的向量投影的概念、作法,在猜想、论证后得到空间向量的投影概念及作法,在此过程中,进一步体会空间向量和平而向量的内在联系,领悟“空间中任意两个向量都是共面的,空间向量的投影可以转化为平面向量的投影”,同时还学会了空间向量投影的直观作法.
(3)空间向量数量积运算的性质.
①.
②.
③.
④.
⑤(交换律).
⑥(分配律).
第⑥条性质可以按如下方式理解:
当,,共面时,根据平面向量数量积的性质可知,结论成立;
当,,不共面时,显然≠0,设即是与同向的单位向量.如图所示,设是个长方体,点与都在直线上,且=,= .
因此,在上的投影为=,在上的投影为=,且==+,+在上的投影为.
注意到=+=,这就说明(+).
在这个式子两边同时乘以,即可知.
设计意图:学生在理解了“空间向量的投影”的概念之后,对投影的认识有进一步提升的需要.另外,从定义出发论证分配律也需要借助投影来实现.以长方体为背景的空间向量图示,能直观呈现空间位置和向量投影
三、例题赏析,感悟“运算”
例2 如图所示长方体 中,是的中点,==2,=4,求:
(1);(2).
解(1)(方法一)因为是长方体,而且==2,所以,
,,
因此.
(方法二)由图可以看出,在上的投影是,而且==1,
注意到与的方向相同,所以等于的长,即==2.
(2)由图可以看出,在上的投影是,而且,
注意到与的方向相反,所以等于的长的相反数,即=-=.
四、归纳总结,作业巩固
1.知识:空间向量数量积的定义、几何意义、运算性质.
2.方法:类比与归纳.
3.思想:数形结合思想、化归转化思想.
4.(1)课后作业:教材第11页练习第3,5题,教材第12页练习第4-6题.
(2)选做作业:仿照教材理解数量积性质(6)的方式,在长方体中设计一个模型验证性质(6).
参考答案:
如图所示,,设,即是与同向的单位向量.
以,为邻边作平行四边形,则
因此,在上的投影为在上的投影为, 在上的投影为.
注意到,这就说明+b·c,
在这个式子两边同时乘以,即可知
板书设计
第2课时 空间向量的数量积 1.空间向量的夹角 定义、取值范围、向量垂直 2.空间向量的数量积 定义、几何意义 3.空间向量数量积的性质 (1) (2) (3) (4) (5)(交换律) (6)(分配律) 4.例题 例1 例2
教学研讨
1.本节课介绍了一种新的空间向量运算(数量积运算),从定义、几何意义、运算性质等维度对这种运算进行研究,并且把教学重心放到对数量积运算的认识上.教学过程中,充分发挥学生的主体作用,通过问题引入、阅读理解、表格填写、交流分享等途径调动学生学习的主动性.
2.空间向量的投影以及数量积的运算性质,代数形式上与平面向量完全一样,但是在几何直观上又有些许不同.这是学生在类比归纳中的一个难点,需要教师适时铺垫引导,逐个突破.教学过程中,充分利用直观的几何图示,帮助学生建立对空间向量投影和分配律的几何内涵的认知.
2 / 2
一、问题引入,提出概念
前面我们刚刚学习了空间向量的加减法、数乘运算,通过学习发现这些运算与平面向量的加减法、数乘运算是完全一致的.我们还学面向量的数量积运算,从定义、几何意义、运算性质等方面认识了数量积运算,那么空间向量的数量积运算是怎样的呢?
设计意图:通过回顾空间向量的加减法、数乘运算的学习经验,让学生体会空间向量与平面向量的内在联系,暗示学生可运用类比的方法学习空间向量的数量积运算.借此,提出“空间向量的数量积”的概念,为后续自主探究、交流分享环节作好铺垫.
二、自主探究,交流分享
1.小组合作,自主探究.
分组:4人一组,每组确定1名组长,组长负责组织讨论、记录,汇报讨论结果.
引导:呈现研究平面向量数量积运算的几个维度,暗示学生探究的方向.
向量的数量积
平面向量 空间向量
向量夹 角的 定义、范围 平面内,给定两个非零向量,,任意在平面内选定一点,作,则大小在内的称为与的夹角,记作.
向量 垂直 如果 ,则称向量与垂直,记作.约定零向量与任意向量都垂直.
数量积定义 平面内,两个非零向量与的数量积(或内积)定义为.规定零向量与任意向量的数量积为0.
向量的数量积
平面向量 空间向量
几何意义 如图所示,过的始点和终点分别向所在的直线作垂线,即可得到向量在向量上的投影,与的数量积等于在上的投影的数量与的长度的乘积.特别地,与单位向量的数量积等于在上的投影的数量.
运算 性质 (1) (2) (3) (4) (5)(交换律) (6)(分配律)
教师巡视、点拨,对讨论过程中个别疑难处进行指导.
提醒:对照表格进行填写,梳理空间向量数量积运算的相关知识.
设计意图:充分发挥学生的主体作用,凸显“以学生为主体的教,在教师引导下的学”的授课模式,让学生“动起来”,让课堂“活起来”.
2.概念辨析,交流分享.
(1)空间向量的夹角.
例1 如图所示是一个正方体,求下列各对向量的夹角:
(1)与;(2)与;(3)与
(4)与.
解(1)由于与的方向相同,所以==45°.
(2)==135°.
(3)==90°.
(4)==180°.
设计意图:通过具体实例的分析讲解,巩固空间向量夹角的概念.
(2)空间向量的投影.
空间向量在向量上的投影,除了按照平面向量的投影的方式得到之外,还可以过的始点和终点分别作与所在直线垂直的平面得到,这可以从下图所示的长方体中看出来,其中向量在棱上,=,因为=,,所以在向量上的投影=.
一般地,给定空间向量和空间中的直线(或平面),过的始点和终点分别作直线(或平面)的垂线,假设垂足为,,则向量称为在直线(或平面)上的投影.
设计意图:学生通过类比平面向量中的向量投影的概念、作法,在猜想、论证后得到空间向量的投影概念及作法,在此过程中,进一步体会空间向量和平而向量的内在联系,领悟“空间中任意两个向量都是共面的,空间向量的投影可以转化为平面向量的投影”,同时还学会了空间向量投影的直观作法.
(3)空间向量数量积运算的性质.
①.
②.
③.
④.
⑤(交换律).
⑥(分配律).
第⑥条性质可以按如下方式理解:
当,,共面时,根据平面向量数量积的性质可知,结论成立;
当,,不共面时,显然≠0,设即是与同向的单位向量.如图所示,设是个长方体,点与都在直线上,且=,= .
因此,在上的投影为=,在上的投影为=,且==+,+在上的投影为.
注意到=+=,这就说明(+).
在这个式子两边同时乘以,即可知.
设计意图:学生在理解了“空间向量的投影”的概念之后,对投影的认识有进一步提升的需要.另外,从定义出发论证分配律也需要借助投影来实现.以长方体为背景的空间向量图示,能直观呈现空间位置和向量投影
三、例题赏析,感悟“运算”
例2 如图所示长方体 中,是的中点,==2,=4,求:
(1);(2).
解(1)(方法一)因为是长方体,而且==2,所以,
,,
因此.
(方法二)由图可以看出,在上的投影是,而且==1,
注意到与的方向相同,所以等于的长,即==2.
(2)由图可以看出,在上的投影是,而且,
注意到与的方向相反,所以等于的长的相反数,即=-=.
四、归纳总结,作业巩固
1.知识:空间向量数量积的定义、几何意义、运算性质.
2.方法:类比与归纳.
3.思想:数形结合思想、化归转化思想.
4.(1)课后作业:教材第11页练习第3,5题,教材第12页练习第4-6题.
(2)选做作业:仿照教材理解数量积性质(6)的方式,在长方体中设计一个模型验证性质(6).
参考答案:
如图所示,,设,即是与同向的单位向量.
以,为邻边作平行四边形,则
因此,在上的投影为在上的投影为, 在上的投影为.
注意到,这就说明+b·c,
在这个式子两边同时乘以,即可知
板书设计
第2课时 空间向量的数量积 1.空间向量的夹角 定义、取值范围、向量垂直 2.空间向量的数量积 定义、几何意义 3.空间向量数量积的性质 (1) (2) (3) (4) (5)(交换律) (6)(分配律) 4.例题 例1 例2
教学研讨
1.本节课介绍了一种新的空间向量运算(数量积运算),从定义、几何意义、运算性质等维度对这种运算进行研究,并且把教学重心放到对数量积运算的认识上.教学过程中,充分发挥学生的主体作用,通过问题引入、阅读理解、表格填写、交流分享等途径调动学生学习的主动性.
2.空间向量的投影以及数量积的运算性质,代数形式上与平面向量完全一样,但是在几何直观上又有些许不同.这是学生在类比归纳中的一个难点,需要教师适时铺垫引导,逐个突破.教学过程中,充分利用直观的几何图示,帮助学生建立对空间向量投影和分配律的几何内涵的认知.
2 / 2
