6.3.7实践与探索---月历、足球[下学期]
文档属性
| 名称 | 6.3.7实践与探索---月历、足球[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 49.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-12-09 00:00:00 | ||
图片预览

文档简介
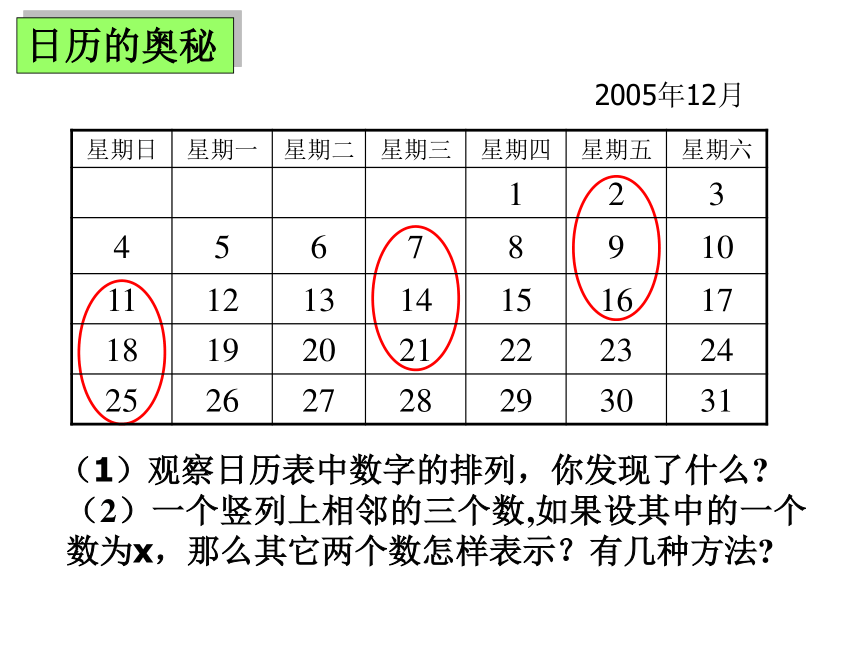
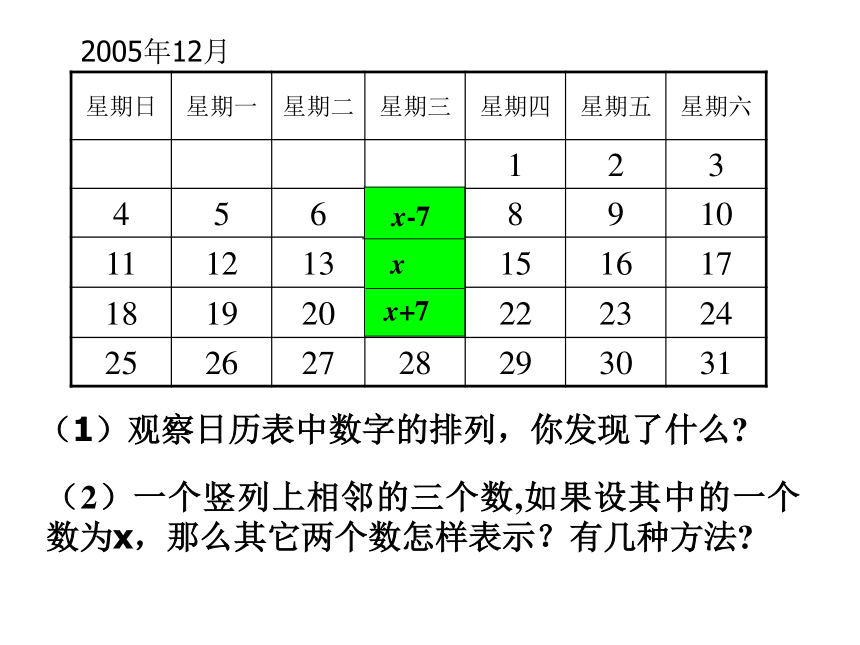
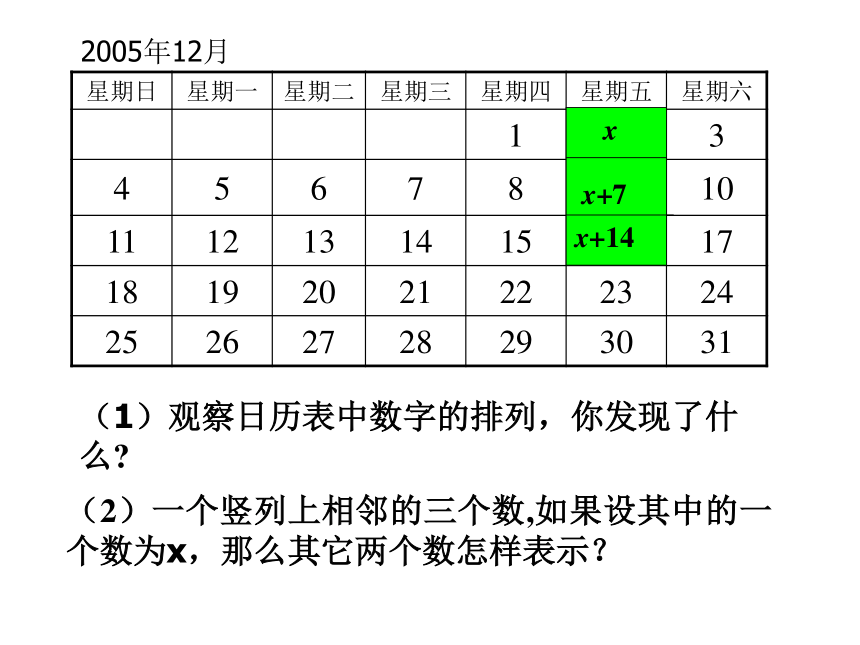
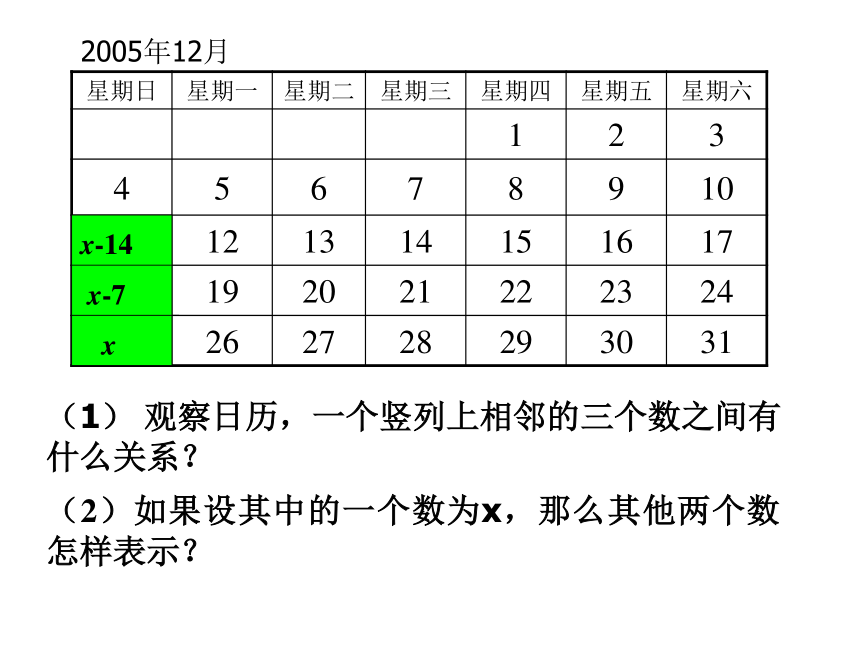
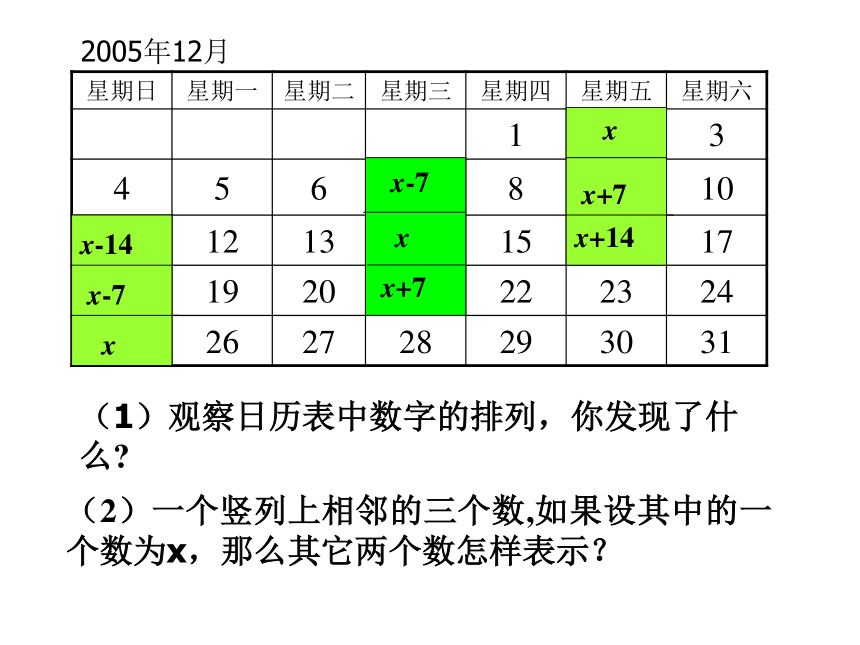
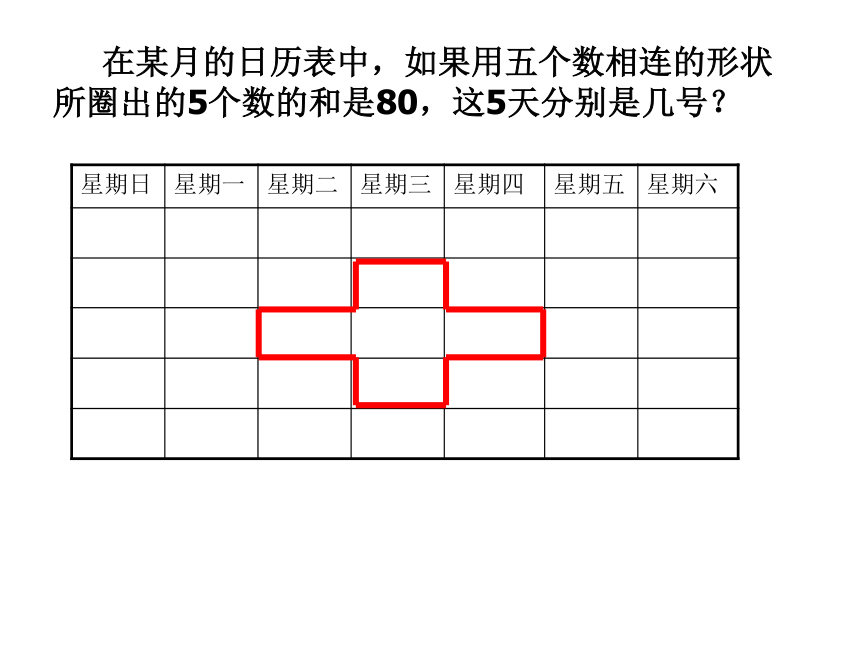
课件17张PPT。6.3.7实践与探索---月历、足球6.3.5实践与探索---月历、足球(1)观察日历表中数字的排列,你发现了什么?(2)一个竖列上相邻的三个数,如果设其中的一个数为x,那么其它两个数怎样表示?有几种方法?2005年12月日历的奥秘xx+7x-72005年12月(1)观察日历表中数字的排列,你发现了什么?(2)一个竖列上相邻的三个数,如果设其中的一个数为x,那么其它两个数怎样表示?有几种方法?xx+7x+142005年12月(1)观察日历表中数字的排列,你发现了什么?(2)一个竖列上相邻的三个数,如果设其中的一个数为x,那么其它两个数怎样表示?xx-7x-14(1) 观察日历,一个竖列上相邻的三个数之间有什么关系?(2)如果设其中的一个数为x,那么其他两个数怎样表示?2005年12月xx-7x-14xx+7x-7xx+7x+142005年12月(1)观察日历表中数字的排列,你发现了什么?(2)一个竖列上相邻的三个数,如果设其中的一个数为x,那么其它两个数怎样表示? 在某月的日历表中,如果用五个数相连的形状所圈出的5个数的和是80,这5天分别是几号?1.右面是一张2005年12月份的月历,1、2、??、30、31个数按一定规律排列成数字阵列,请你尽可能多地发现这个数字阵列存在的规律。解:竖着看:横着看:斜着看:①每列都是从上往下依次增加7的一列数;②每列中的数被7除,各自的余数相同;③有5个数的那一列的平均数等于中间位置上的数.①每排都是从左往右依次增加1的一排数;②每一排相邻奇数个数的平均数都等于中间位置上的数;③有7个数字的那一排的数字和能被7整除.①从左上向右下是每个数依次增加8的一列数;②从右上向左下是每个数递增6的一列数.解:与周围数联系看:①靠在一起的四个数所组成的正方形,对角上的两个数的和相等;②靠在一起的九个数所组成的正方形,两条对角线上的三个数的和相等; ③靠在一起的十六个数所组成的正方形,两条对角线上的四个数的和相等; ④任意一个“十字型”,所有数的平均数等于中间位置上的数.2.根据你在月历上发现的规律,解答下面的问题:(1)在某张月历上,设3?3方阵(如下图1)的中心数是x,方阵中9个数之和是126.则可列出方程_______________.解得x=___________________.这个方阵中的最小数是_______________,最大数是_____________________;图1图2(2)在“H”字型的数阵(如图2)中.7个数字之和是126,请你用至少两种不同的方法求出这个数阵中的最小数和最大数;图3(3)在2?2的平行四边形数阵(如下图3)中,四个数字的和是62.求出这四个数(方法不限);(4)在某张月历上,一个月内的五个星期日正好在同一列,且它们的日期数之和是80,请你用多种方法算出本月内第一个星期一是几号?趣味数学足球上的数学题 2002年,中国队第一次打入世界杯决赛圈,这一年中考,足球上的数学也就成了中考命题的热点,比如,下面几个题目.1.有一种足球是由32块黑白相间的牛皮缝制而成的(如图),黑皮可看作正五边形,白皮可看作正六边形.设白皮有x块,则黑皮有(32-x)块,每一块白皮有6条边,共6x条边,因每一块白皮有三条边和黑皮连在一起,故黑皮共有3x条边.要求出黑皮、白皮的块数,列出的方程正确的是( )(A)3x=32-x(B)3x=5(32-x)(C) 5x=3(32-x)(D) 6x=32-x2.小明和小刚在踢足球休息之余研究起足球上的黑白块的个数来,发现黑块呈五边形,白块呈六边形,如下图所示.由于黑白相间在球体上,小明好不容易才数清了黑块共12块,小刚怎么也点不清白块的个数,你能帮助他们解决这一问题吗?3.为庆祝中国首次进入世界杯赛,曙光体育器材厂赠送一批足球给希望中学足球队.若足球队每人领一个球,则少6个球;若足球队每2人领一个球,则余6个球.问这批足球共有多少个?小明领到足球后十分高兴,就仔细研究起足球上的黑白块来,结果发现,黑块呈五边形,白块呈六边形,黑白相间在 球体上,黑块共有12块,问白块有多少块?
