23.3实践与探索三[上学期]

课件14张PPT。 课 题22.3 实践与探索 课前热身解下列方程：比一比，看谁算得快！方法提炼1、一元二次方程的几种基本解法：特别地，一元二次方程①直接开平方法 ②因式分解法
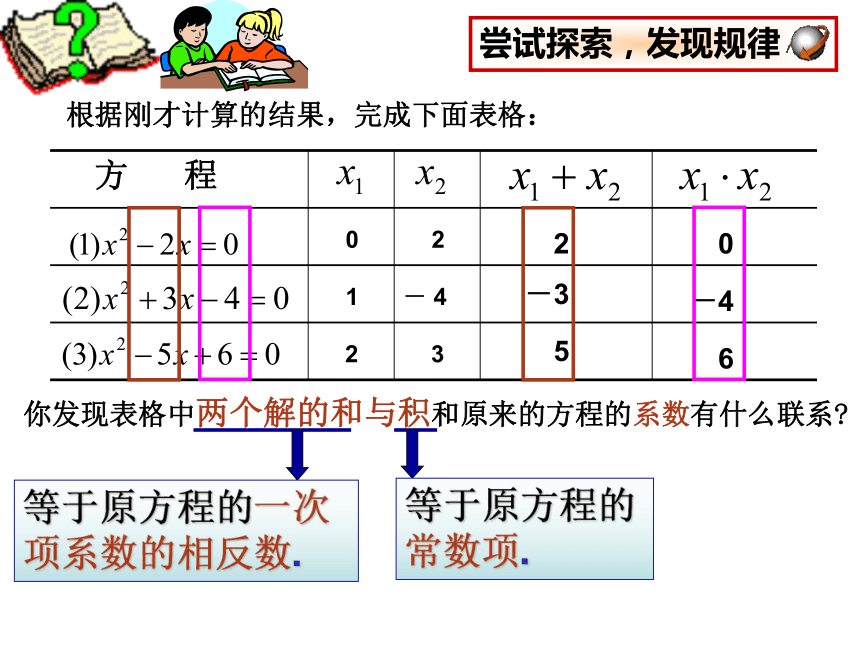
③配方法 ④公式法 ⑤换元法根据刚才计算的结果，完成下面表格：你发现表格中两个解的和与积和原来的方程的系数有什么联系?02 3 2－ 412－350－46等于原方程的一次项系数的相反数.等于原方程的常数项.尝试探索，发现规律探 索 对于关于x的方程 x2+px+q=0（ p，q为已知常数,
p2-4q≥0),试用求根公式求出它的两个解

x1 = 、x2 = ,
算一算x1+x2、x1●x2的值,你能得出什么结果?与上面发现的现象是否一致？x1+x2=－p－p2-4q≥01我的发现如果一元二次方程
的两个实数根是 ，那么说出下列各方程的两实根之和与两实根之积：方程无实根试一试知识品味 知识应用，体验成功分 析：
（1）本题的知识点是解一元二次方程及其根与系数的关系，它的答案不唯一。
（2）在选取m的值时，应注意题设的限定条件，还要以简单为原则。
（3）在求代数式的值时，有两种方法：一是直接代入；二是利用根与系数的关系。（2）不解方程，可以利用一元二次方程根与系数求关于
的代数式的值。如： 题例回顾：（1）学习和使用一元二次方程根与系数关系时，要注意定理的前提条件：
A、是在一元二次方程的条件下，即注意二次项系数不为零。
B、是在有实数根的条件下，即△≥0。（两者缺一不可）。 知识应用，体验成功 中考链接，能力测试AD 中考链接，能力测试B 小结反思，延伸提高1、如果一元二次方程 的两个实数根
是 ，那么2、在应用一元二次方程根与系数的关系时，应注意
条件：3、在一次数学发现过程中，将经历实验、观察、分析、对比、归纳、再实验等数学思维活动，最后是数学证明。只有这样，一个数学结论才能被认可。探 索如果 是一元二次方程
的两个实数根，那么方程的两根与系数a、b、c之间
又有什么关系呢？请你解下列方程，然后对照方程，尝试找出
根与系数的联系。请把你的发现与大家一起分享！ 作业布置，自我测试1、见作业本（略）
2、自我测试：见附页