北师大版数学八年级下册 1.2 直角三角形课件 (共18张PPT)
文档属性
| 名称 | 北师大版数学八年级下册 1.2 直角三角形课件 (共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 197.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 20:26:14 | ||
图片预览






文档简介
(共18张PPT)
直角三角形全等的判定
(HL)
北师大版八年级下册1.2直角三角形
1、判定三角形全等的方法有: 。
2、如图,AB⊥BE于B,DE⊥BE于E,根据下列条件△ABC与△DEF全等吗?理由是什么?
SAS、ASA、AAS、SSS
(1) AB=DE,BC=EF
(2)∠ A=∠D,AC=DF
(3) AB=DE ,AC=DF
A
C
B
D
E
F
第七张
复习
探究
第一组
画一个Rt△ABC,使∠C=90°, CA=3cm, AB=5cm。
第二组
画一个Rt△ABC,使∠C=90°, CA=2.5cm, AB=6.5cm。
把画好的三角形剪下来,同组之间比较一下,它们全等吗
演示1
演示2
已知:在Rt△ABC 和Rt△A′B′C′中,
∠C=∠C′=90°,AB=A′B′,BC=B′C′.
求证:Rt△ABC ≌Rt△A′B′C′.
证明:在Rt△ABC中,AC2=AB2一BC2(勾股定理).
又∵在Rt△ A′B′C′中,
A′C′2=A′B′2—B′C′2 (勾股定理).
∴AB=A′B′,BC=B′C′,AC=A′C′.
∴Rt△ABC≌Rt△A′B′C′(SSS)
结论
由此得到
直角三角形全等的判定定理:
斜边、直角边定理 斜边和一条直角边对应相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL”).
在使用“HL”时,同学们应注意什么
(1)“HL”是仅适用于直角三角形的特殊方法.
(2)注意对应相等.
书写格式:
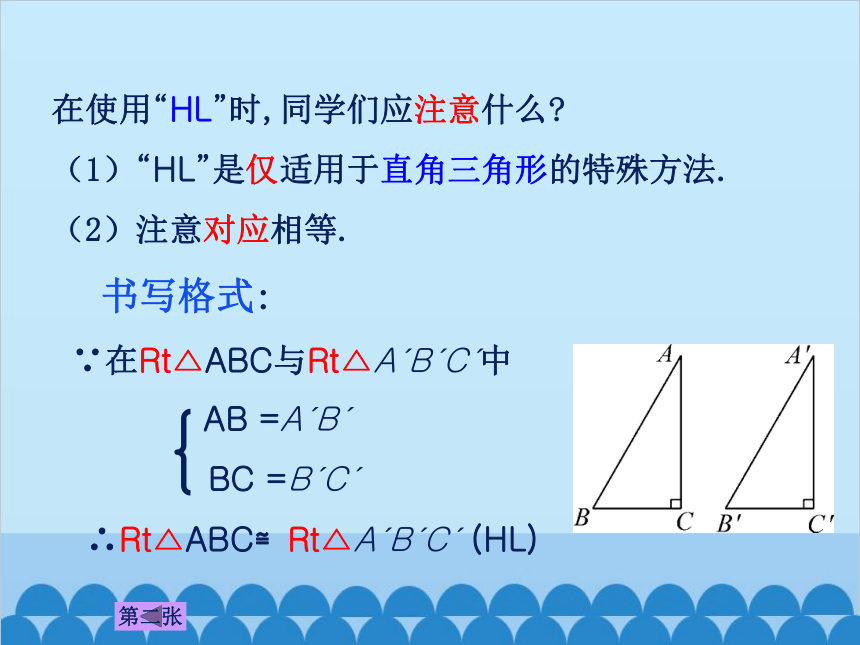
∵在Rt△ABC与Rt△A′B′C′中
AB =A′B′
BC =B′C′
∴Rt△ABC≌Rt△A′B′C′ (HL)
第二张
想一想
到现在为止,你能够用几种方法说明两个直角三角形全等?
答:有五种:SAS、ASA、AAS、SSS、HL
举例
例1.已知:如图,AB⊥BD,CD⊥BD,AD=BC.
求证:AD∥BC.
证明: ∵AB⊥BD,CD⊥BD,
∴∠ABD=∠CDB=90°.
在Rt△ABD和Rt△CDB中,
AD=CB,
BD=DB,
∴Rt△ABD≌Rt△CDB(HL)
∴∠ADB=∠CBD
∴AD∥BC.
A
C
B
D
例2.已知:如图,AC⊥BC,BD⊥AD, AC=BD, 求证:AD=BC.
证明:∵AC⊥BC,BD⊥AD,
∴∠D=∠C=90°.
在Rt△ABC和Rt△BAD中,
AB=BA,
AC=BD,
∴Rt△ABC≌Rt△BAD(HL).
∴BC=AD.
C
B
A
D
A
D
A
D
B
A
D
C
B
A
D
D
A
D
A
D
C
举例
举例
例3.已知:如图,AC=BD,AD⊥AC,BC⊥BD.
求证:AD=BC.
A
B
D
C
证明:连接DC.
∵ AD⊥AC,BC⊥BD,
∴∠A=∠B=90°.
在Rt△ADC和Rt△BCD中,
DC=CD,
AC=BD,
∴Rt△ADC≌Rt△BCD(HL).
∴AD=BC.
练习
1.如图,△ABC中,AB=AC,AD是高,
则_____≌______,依据是________ ,
由全等得出BD=____,∠BAD=____.
A
D
C
B
2.如图,E、B、F、C在同一条直线上,
若∠D=∠A=90°,EB=FC,AB=DF,
则△ ABC≌_____,全等的根据是_____.
练习
A
D
C
E
B
F
练习
3.如图,已知AB⊥CF,DE ⊥CF,垂足分别为B、E,AB=DE.请添加一个适当条件,使△ABC≌△DEF,并说明理由.
添加条件:________,理由是:______.
A
F
B
D
E
C
练习
4.已知:如图,AE⊥AB,BC⊥AB,AE=AB,ED=AC.求证:ED⊥AC.
E
A
D
F
C
B
证明:∵AE⊥AB,BC⊥AB,
∴∠EAD=∠ABC=90°.
在Rt△EAD和Rt△ABC中,
ED=AC,
EA=AB,
∴ Rt△EAD≌Rt△ABC (HL).
∴∠AED=∠BAC.
∵∠EAF+∠BAC=90°,
∴∠EAF+∠AED=90°,
∴∠EFA=90°,
∴ED⊥AC.
通过本节课的学习你有什么收获?
小结
直角三角形全等的判定
(HL)
北师大版八年级下册1.2直角三角形
1、判定三角形全等的方法有: 。
2、如图,AB⊥BE于B,DE⊥BE于E,根据下列条件△ABC与△DEF全等吗?理由是什么?
SAS、ASA、AAS、SSS
(1) AB=DE,BC=EF
(2)∠ A=∠D,AC=DF
(3) AB=DE ,AC=DF
A
C
B
D
E
F
第七张
复习
探究
第一组
画一个Rt△ABC,使∠C=90°, CA=3cm, AB=5cm。
第二组
画一个Rt△ABC,使∠C=90°, CA=2.5cm, AB=6.5cm。
把画好的三角形剪下来,同组之间比较一下,它们全等吗
演示1
演示2
已知:在Rt△ABC 和Rt△A′B′C′中,
∠C=∠C′=90°,AB=A′B′,BC=B′C′.
求证:Rt△ABC ≌Rt△A′B′C′.
证明:在Rt△ABC中,AC2=AB2一BC2(勾股定理).
又∵在Rt△ A′B′C′中,
A′C′2=A′B′2—B′C′2 (勾股定理).
∴AB=A′B′,BC=B′C′,AC=A′C′.
∴Rt△ABC≌Rt△A′B′C′(SSS)
结论
由此得到
直角三角形全等的判定定理:
斜边、直角边定理 斜边和一条直角边对应相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL”).
在使用“HL”时,同学们应注意什么
(1)“HL”是仅适用于直角三角形的特殊方法.
(2)注意对应相等.
书写格式:
∵在Rt△ABC与Rt△A′B′C′中
AB =A′B′
BC =B′C′
∴Rt△ABC≌Rt△A′B′C′ (HL)
第二张
想一想
到现在为止,你能够用几种方法说明两个直角三角形全等?
答:有五种:SAS、ASA、AAS、SSS、HL
举例
例1.已知:如图,AB⊥BD,CD⊥BD,AD=BC.
求证:AD∥BC.
证明: ∵AB⊥BD,CD⊥BD,
∴∠ABD=∠CDB=90°.
在Rt△ABD和Rt△CDB中,
AD=CB,
BD=DB,
∴Rt△ABD≌Rt△CDB(HL)
∴∠ADB=∠CBD
∴AD∥BC.
A
C
B
D
例2.已知:如图,AC⊥BC,BD⊥AD, AC=BD, 求证:AD=BC.
证明:∵AC⊥BC,BD⊥AD,
∴∠D=∠C=90°.
在Rt△ABC和Rt△BAD中,
AB=BA,
AC=BD,
∴Rt△ABC≌Rt△BAD(HL).
∴BC=AD.
C
B
A
D
A
D
A
D
B
A
D
C
B
A
D
D
A
D
A
D
C
举例
举例
例3.已知:如图,AC=BD,AD⊥AC,BC⊥BD.
求证:AD=BC.
A
B
D
C
证明:连接DC.
∵ AD⊥AC,BC⊥BD,
∴∠A=∠B=90°.
在Rt△ADC和Rt△BCD中,
DC=CD,
AC=BD,
∴Rt△ADC≌Rt△BCD(HL).
∴AD=BC.
练习
1.如图,△ABC中,AB=AC,AD是高,
则_____≌______,依据是________ ,
由全等得出BD=____,∠BAD=____.
A
D
C
B
2.如图,E、B、F、C在同一条直线上,
若∠D=∠A=90°,EB=FC,AB=DF,
则△ ABC≌_____,全等的根据是_____.
练习
A
D
C
E
B
F
练习
3.如图,已知AB⊥CF,DE ⊥CF,垂足分别为B、E,AB=DE.请添加一个适当条件,使△ABC≌△DEF,并说明理由.
添加条件:________,理由是:______.
A
F
B
D
E
C
练习
4.已知:如图,AE⊥AB,BC⊥AB,AE=AB,ED=AC.求证:ED⊥AC.
E
A
D
F
C
B
证明:∵AE⊥AB,BC⊥AB,
∴∠EAD=∠ABC=90°.
在Rt△EAD和Rt△ABC中,
ED=AC,
EA=AB,
∴ Rt△EAD≌Rt△ABC (HL).
∴∠AED=∠BAC.
∵∠EAF+∠BAC=90°,
∴∠EAF+∠AED=90°,
∴∠EFA=90°,
∴ED⊥AC.
通过本节课的学习你有什么收获?
小结
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
