沪科版九年级数学25.2圆的对称性(第二课时)垂径定理
文档属性
| 名称 | 沪科版九年级数学25.2圆的对称性(第二课时)垂径定理 |

|
|
| 格式 | zip | ||
| 文件大小 | 234.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-28 00:00:00 | ||
图片预览



文档简介
课件29张PPT。九年级数学(下)第25章圆25.2 圆的对称性(2)
-----垂径定理
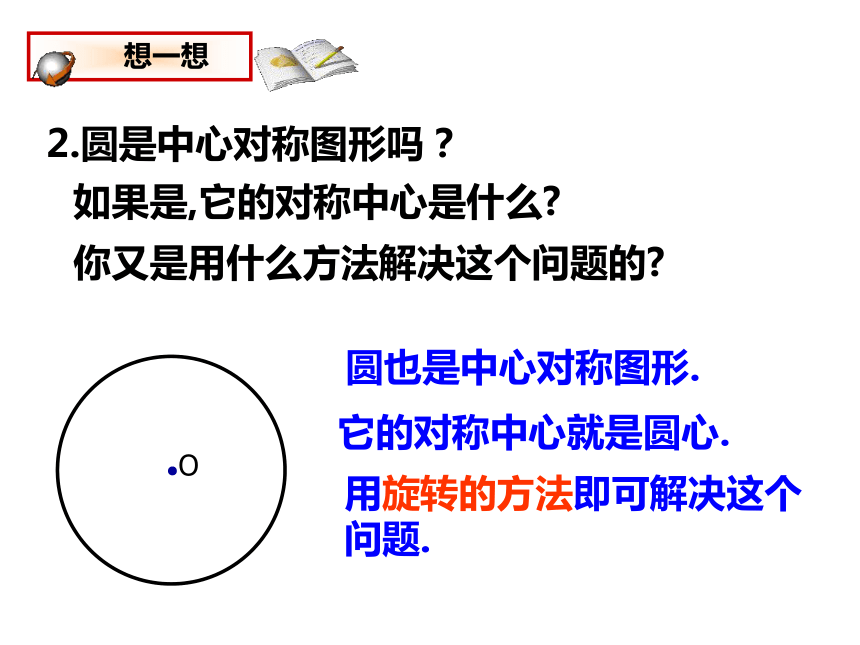
1.圆是轴对称图形吗?你是用什么方法解决这个问题的?圆是轴对称图形.其对称轴是任意一条过圆心的直线.如果是,它的对称轴是什么?用折叠的方法即可解决这个问题.你能找到多少条对称轴?2.圆是中心对称图形吗?你又是用什么方法解决这个问题的?圆也是中心对称图形.它的对称中心就是圆心.如果是,它的对称中心是什么?用旋转的方法即可解决这个问题.观察猜想.?
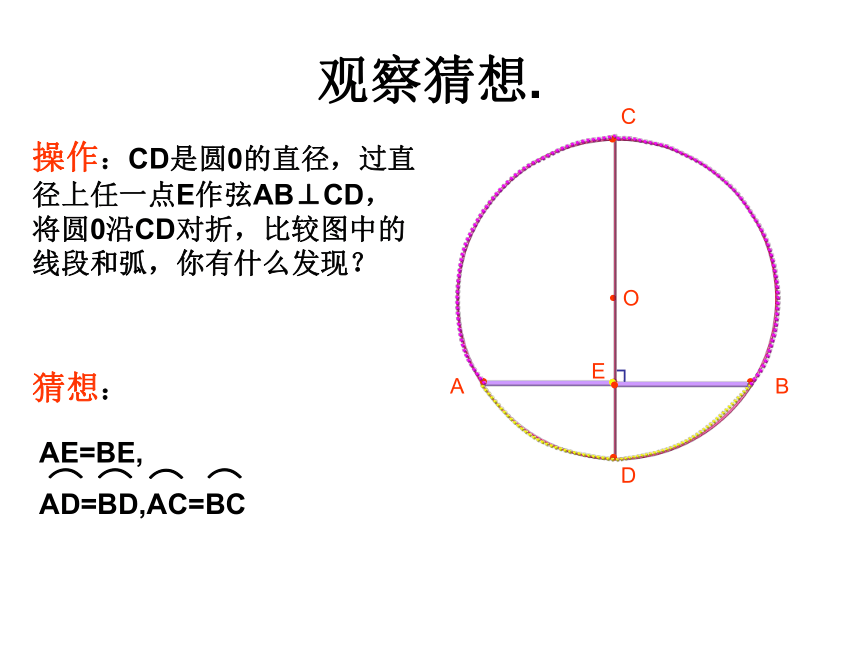
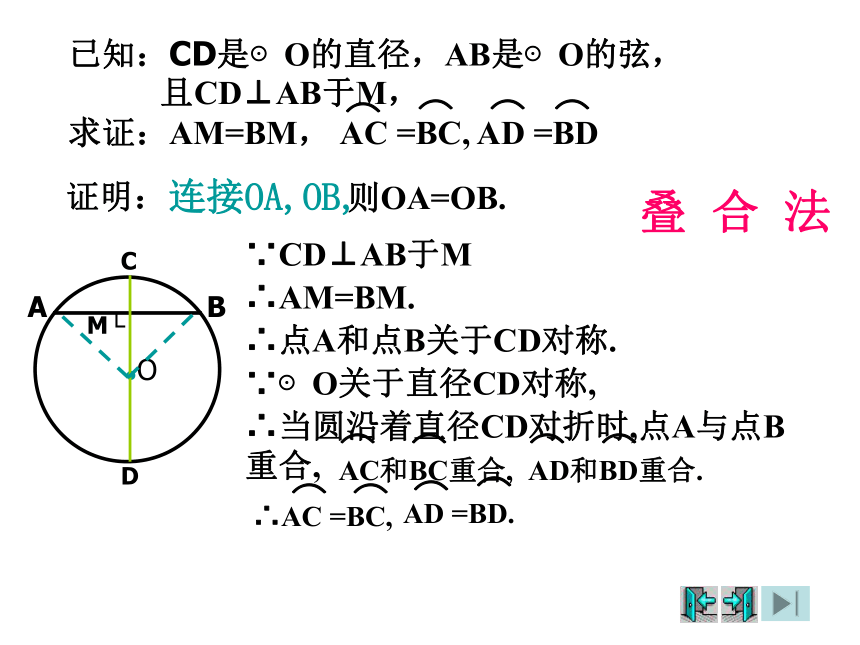
操作:CD是圆0的直径,过直径上任一点E作弦AB⊥CD,将圆0沿CD对折,比较图中的线段和弧,你有什么发现?猜想:连接OA,OB,则OA=OB.∴AM=BM.∴点A和点B关于CD对称.∵⊙O关于直径CD对称,∴当圆沿着直径CD对折时,点A与点B重合,∵CD⊥AB于M证明:已知:CD是⊙O的直径,AB是⊙O的弦,
且CD⊥AB于M,
求证:AM=BM, AC =BC, AD =BD
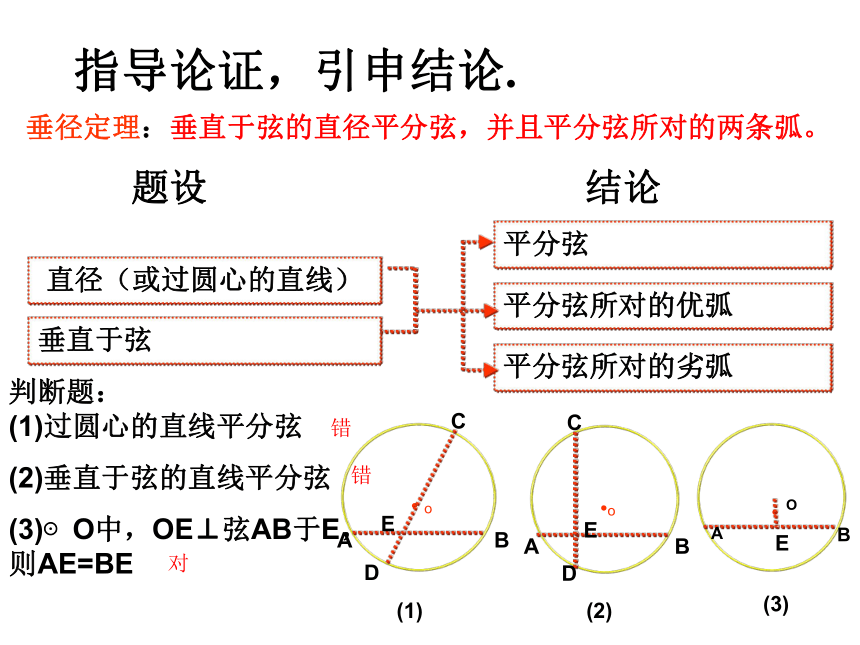
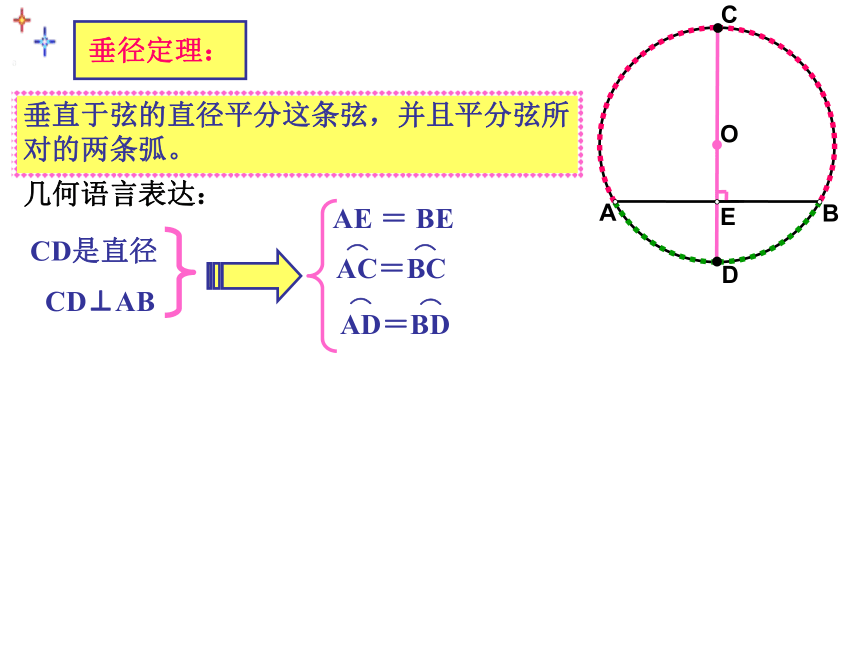
⌒⌒⌒⌒叠 合 法错指导论证,引申结论.垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧。判断题: (1)过圆心的直线平分弦
(2)垂直于弦的直线平分弦
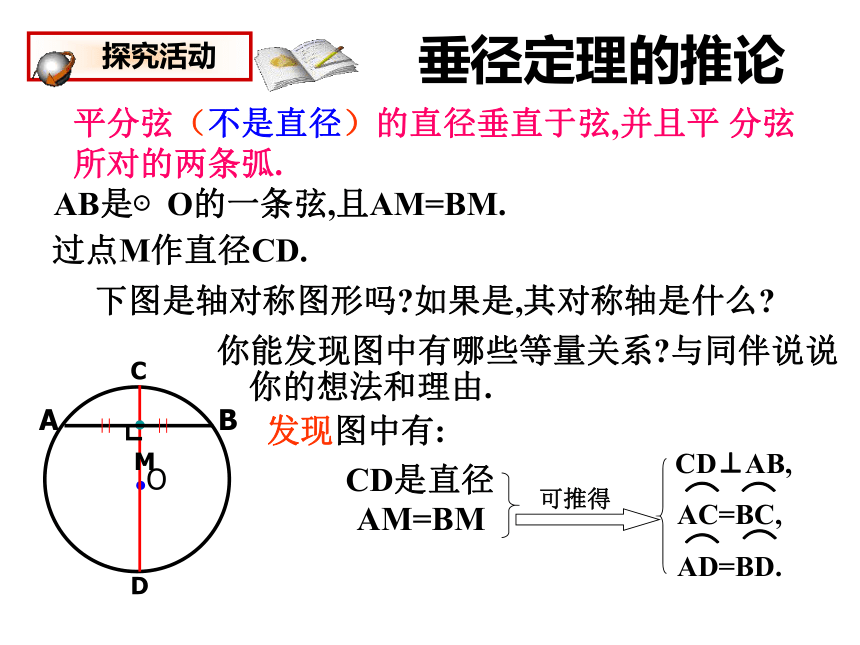
(3)⊙O中,OE⊥弦AB于E,则AE=BE题设结论错对BAOE垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。几何语言表达:CD⊥AB,垂径定理的推论 AB是⊙O的一条弦,且AM=BM.你能发现图中有哪些等量关系?与同伴说说你的想法和理由.过点M作直径CD.下图是轴对称图形吗?如果是,其对称轴是什么?发现图中有: CD是直径 AM=BM┗平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.根据垂径定理与推论可知对于一个圆和一条直线来说。如果具备(1)过圆心 (2)垂直于弦 (3)平分弦(4)
平分弦所对的优弧 (5)平分弦所对的劣弧上述五个条件中的任何两个条件都可以推出其他三个结论注意下列图形是否具备垂径定理的条件?火眼金睛 如果圆的两条弦互相平行,那么这两条弦所夹的弧相等吗? 提示: 这两条弦在圆中位置有两种情况: 圆的两条平行弦所夹的弧相等. 1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(弧所对是弦的长)为 37.4 m,拱高(弧的中点到弦的距离,也叫弓形高)为7.2m,求桥拱的半径(精确到0.1m).赵州石拱桥解:由题设得在Rt△OAD中,由勾股定理,得解得 R≈27.9(m).答:赵州石拱桥的桥拱半径约为27.9m.例2、已知:如图在⊙O中,弦AB的长是8cm,圆心O到AB的距离为3cm,求⊙O的半径解:连结OA,作OE⊥AB于E,则OE=3cm,AE=BE
∵AB=8cm
∴AE=4cm
在Rt中有 OA=
=
=5cm
∴ ⊙O的半径为5cm
解后指出:从例2看出圆的半径OA,圆心到弦的垂线段OE及半弦长AE构成Rt△AOE.把垂径定理和勾股定理结合起来,解决这类问题就显得很容易了。例3 如图,一条公路的转变处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且OE⊥CD垂足为F,EF=90m.求这段弯路的半径.解:连接OC. 例4、如图,圆O与矩形ABCD交于E、F、H,EF=10,HG=6,AH=4.求BE的长.解:过O作OM⊥BC于M,交AD于N,
∵矩形ABCD , ∴AD∥BC, ∴ OM⊥ AD
∴ EM=1/2EF=5,HN=1/2HG=3
∴AN=AH+HN=4+3=7, ∴ BM=7
∴BE= BM- EM =7-5=21.在⊙O中,若CD ⊥AB于M,AB为直径,则下列结论不正确的是( )练一练2.已知⊙O的直径AB=10,弦CD ⊥AB,垂足为M,OM=3,则CD= .3.在⊙O中,CD ⊥AB于M,AB为直径,若CD=10,AM=1,则⊙O的半径是 . C813注意:解决有关弦的问题时,半径是常用的一种辅助线的添法.往往结合勾股定理计算。 判断:
⑴垂直于弦的直线平分这条弦,并且平分弦所对的两条弧. ( )
⑵平分弦的直径一定垂直于这条弦. ( )
(3)弦的垂直平分线一定经过圆心. ( )?√练一练? 已知如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D两点。
求证:AC=BD证明:过O作OE⊥AB于E,解后指出:在圆中,解有关弦的问题时,常常需要作出“垂直于弦的直径”作为辅助线,实际上,往往只需从圆心作弦的垂线段。练一练则 AE=BE,CE=DE∴AE-CE=BE-DE即AC=BD(1)如图,已知⊙O的半径为 6 cm,弦 AB与半径 OA的夹角为 30 °,求弦 AB 的长.OAOCABM(2)如图,已知⊙O的半径为 6 cm,弦 AB与半径 OC互相平分,交点为 M , 求 弦 AB 的长.630°EB练一练E小结: 解决有关弦的问题,经常是过圆心作弦的垂线,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件。E.ACDBO.ABO垂径定理的应用在直径为650mm的圆柱形油槽内装入一些油后,截面如图所示.若油面宽AB = 600mm,求油的最大深度. 垂径定理的应用在直径为650mm的圆柱形油槽内装入一些油后,截面如图所示.若油面宽AB = 600mm,求油的最大深度. DC课堂小结1、本节课主要学习了(1)圆的轴对称性;(2)垂径定理及推论. 2、有关弦的问题,常常需要过圆心作弦的垂线段,这是一条非 常重要的辅助线.圆心到弦的距离、半径、弦长构成直角三 角形,便将问题转化为解直角三角形的问题. 3、垂径定理的证明,是通过“实验——观察——猜想——证明” 实现的,体现了实践的观点、运动变化的观点和先猜想后 证明的观点,定理的引入还应用了从特殊到一般的思想方法.
r4r-4知识结构
思考题已知:AB是⊙O直径,CD是弦,AE⊥CD,BF⊥CD
求证:EC=DF如图,已知圆O的直径AB与 弦CD相交于G,AE⊥CD于E, BF⊥CD于F,且圆O的半径为
10㎝,CD=16 ㎝,求AE-BF的长。
船能过拱桥吗2 . 如图,某地有一圆弧形拱桥,桥下水面宽为7.2米,拱顶高出水面2.4米.现有一艘宽3米、船舱顶部为长方形并高出水面2米的货船要经过这里,此货船能顺利通过这座拱桥吗?船能过拱桥吗解:如图,用 表示桥拱, 所在圆的圆心为O,半径为Rm,
经过圆心O作弦AB的垂线OD,D为垂足,与 相交于点C.根
据垂径定理,D是AB的中点,C是 的中点,CD就是拱高.
由题设得在Rt△OAD中,由勾股定理,得解得 R≈3.9(m).在Rt△ONH中,由勾股定理,得∴此货船能顺利通过这座拱桥.
-----垂径定理
1.圆是轴对称图形吗?你是用什么方法解决这个问题的?圆是轴对称图形.其对称轴是任意一条过圆心的直线.如果是,它的对称轴是什么?用折叠的方法即可解决这个问题.你能找到多少条对称轴?2.圆是中心对称图形吗?你又是用什么方法解决这个问题的?圆也是中心对称图形.它的对称中心就是圆心.如果是,它的对称中心是什么?用旋转的方法即可解决这个问题.观察猜想.?
操作:CD是圆0的直径,过直径上任一点E作弦AB⊥CD,将圆0沿CD对折,比较图中的线段和弧,你有什么发现?猜想:连接OA,OB,则OA=OB.∴AM=BM.∴点A和点B关于CD对称.∵⊙O关于直径CD对称,∴当圆沿着直径CD对折时,点A与点B重合,∵CD⊥AB于M证明:已知:CD是⊙O的直径,AB是⊙O的弦,
且CD⊥AB于M,
求证:AM=BM, AC =BC, AD =BD
⌒⌒⌒⌒叠 合 法错指导论证,引申结论.垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧。判断题: (1)过圆心的直线平分弦
(2)垂直于弦的直线平分弦
(3)⊙O中,OE⊥弦AB于E,则AE=BE题设结论错对BAOE垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。几何语言表达:CD⊥AB,垂径定理的推论 AB是⊙O的一条弦,且AM=BM.你能发现图中有哪些等量关系?与同伴说说你的想法和理由.过点M作直径CD.下图是轴对称图形吗?如果是,其对称轴是什么?发现图中有: CD是直径 AM=BM┗平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.根据垂径定理与推论可知对于一个圆和一条直线来说。如果具备(1)过圆心 (2)垂直于弦 (3)平分弦(4)
平分弦所对的优弧 (5)平分弦所对的劣弧上述五个条件中的任何两个条件都可以推出其他三个结论注意下列图形是否具备垂径定理的条件?火眼金睛 如果圆的两条弦互相平行,那么这两条弦所夹的弧相等吗? 提示: 这两条弦在圆中位置有两种情况: 圆的两条平行弦所夹的弧相等. 1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(弧所对是弦的长)为 37.4 m,拱高(弧的中点到弦的距离,也叫弓形高)为7.2m,求桥拱的半径(精确到0.1m).赵州石拱桥解:由题设得在Rt△OAD中,由勾股定理,得解得 R≈27.9(m).答:赵州石拱桥的桥拱半径约为27.9m.例2、已知:如图在⊙O中,弦AB的长是8cm,圆心O到AB的距离为3cm,求⊙O的半径解:连结OA,作OE⊥AB于E,则OE=3cm,AE=BE
∵AB=8cm
∴AE=4cm
在Rt中有 OA=
=
=5cm
∴ ⊙O的半径为5cm
解后指出:从例2看出圆的半径OA,圆心到弦的垂线段OE及半弦长AE构成Rt△AOE.把垂径定理和勾股定理结合起来,解决这类问题就显得很容易了。例3 如图,一条公路的转变处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且OE⊥CD垂足为F,EF=90m.求这段弯路的半径.解:连接OC. 例4、如图,圆O与矩形ABCD交于E、F、H,EF=10,HG=6,AH=4.求BE的长.解:过O作OM⊥BC于M,交AD于N,
∵矩形ABCD , ∴AD∥BC, ∴ OM⊥ AD
∴ EM=1/2EF=5,HN=1/2HG=3
∴AN=AH+HN=4+3=7, ∴ BM=7
∴BE= BM- EM =7-5=21.在⊙O中,若CD ⊥AB于M,AB为直径,则下列结论不正确的是( )练一练2.已知⊙O的直径AB=10,弦CD ⊥AB,垂足为M,OM=3,则CD= .3.在⊙O中,CD ⊥AB于M,AB为直径,若CD=10,AM=1,则⊙O的半径是 . C813注意:解决有关弦的问题时,半径是常用的一种辅助线的添法.往往结合勾股定理计算。 判断:
⑴垂直于弦的直线平分这条弦,并且平分弦所对的两条弧. ( )
⑵平分弦的直径一定垂直于这条弦. ( )
(3)弦的垂直平分线一定经过圆心. ( )?√练一练? 已知如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D两点。
求证:AC=BD证明:过O作OE⊥AB于E,解后指出:在圆中,解有关弦的问题时,常常需要作出“垂直于弦的直径”作为辅助线,实际上,往往只需从圆心作弦的垂线段。练一练则 AE=BE,CE=DE∴AE-CE=BE-DE即AC=BD(1)如图,已知⊙O的半径为 6 cm,弦 AB与半径 OA的夹角为 30 °,求弦 AB 的长.OAOCABM(2)如图,已知⊙O的半径为 6 cm,弦 AB与半径 OC互相平分,交点为 M , 求 弦 AB 的长.630°EB练一练E小结: 解决有关弦的问题,经常是过圆心作弦的垂线,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件。E.ACDBO.ABO垂径定理的应用在直径为650mm的圆柱形油槽内装入一些油后,截面如图所示.若油面宽AB = 600mm,求油的最大深度. 垂径定理的应用在直径为650mm的圆柱形油槽内装入一些油后,截面如图所示.若油面宽AB = 600mm,求油的最大深度. DC课堂小结1、本节课主要学习了(1)圆的轴对称性;(2)垂径定理及推论. 2、有关弦的问题,常常需要过圆心作弦的垂线段,这是一条非 常重要的辅助线.圆心到弦的距离、半径、弦长构成直角三 角形,便将问题转化为解直角三角形的问题. 3、垂径定理的证明,是通过“实验——观察——猜想——证明” 实现的,体现了实践的观点、运动变化的观点和先猜想后 证明的观点,定理的引入还应用了从特殊到一般的思想方法.
r4r-4知识结构
思考题已知:AB是⊙O直径,CD是弦,AE⊥CD,BF⊥CD
求证:EC=DF如图,已知圆O的直径AB与 弦CD相交于G,AE⊥CD于E, BF⊥CD于F,且圆O的半径为
10㎝,CD=16 ㎝,求AE-BF的长。
船能过拱桥吗2 . 如图,某地有一圆弧形拱桥,桥下水面宽为7.2米,拱顶高出水面2.4米.现有一艘宽3米、船舱顶部为长方形并高出水面2米的货船要经过这里,此货船能顺利通过这座拱桥吗?船能过拱桥吗解:如图,用 表示桥拱, 所在圆的圆心为O,半径为Rm,
经过圆心O作弦AB的垂线OD,D为垂足,与 相交于点C.根
据垂径定理,D是AB的中点,C是 的中点,CD就是拱高.
由题设得在Rt△OAD中,由勾股定理,得解得 R≈3.9(m).在Rt△ONH中,由勾股定理,得∴此货船能顺利通过这座拱桥.
