沪科版九年级数学25.2圆的对称性(第三课时)圆心角
文档属性
| 名称 | 沪科版九年级数学25.2圆的对称性(第三课时)圆心角 |  | |
| 格式 | zip | ||
| 文件大小 | 323.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-28 15:35:01 | ||
图片预览

文档简介
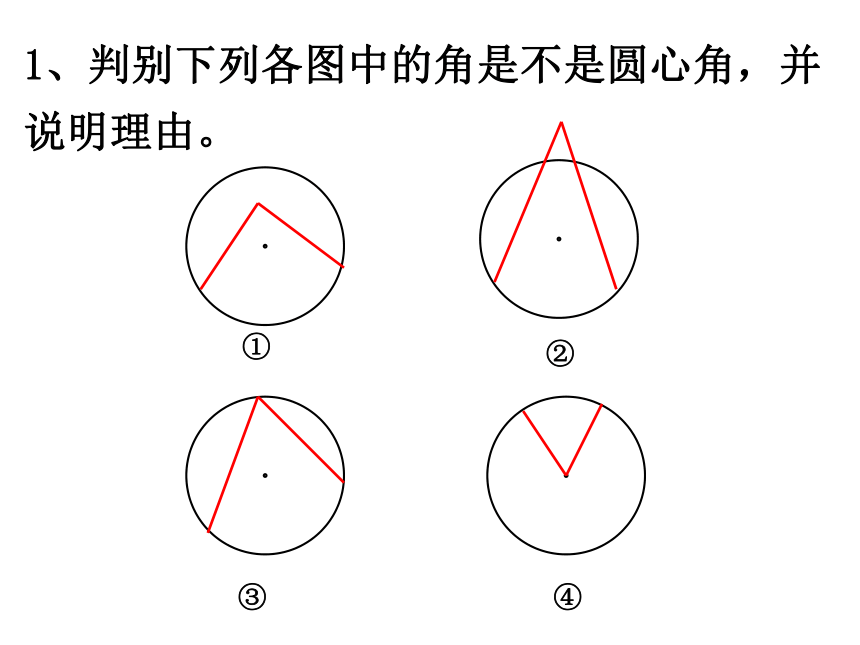
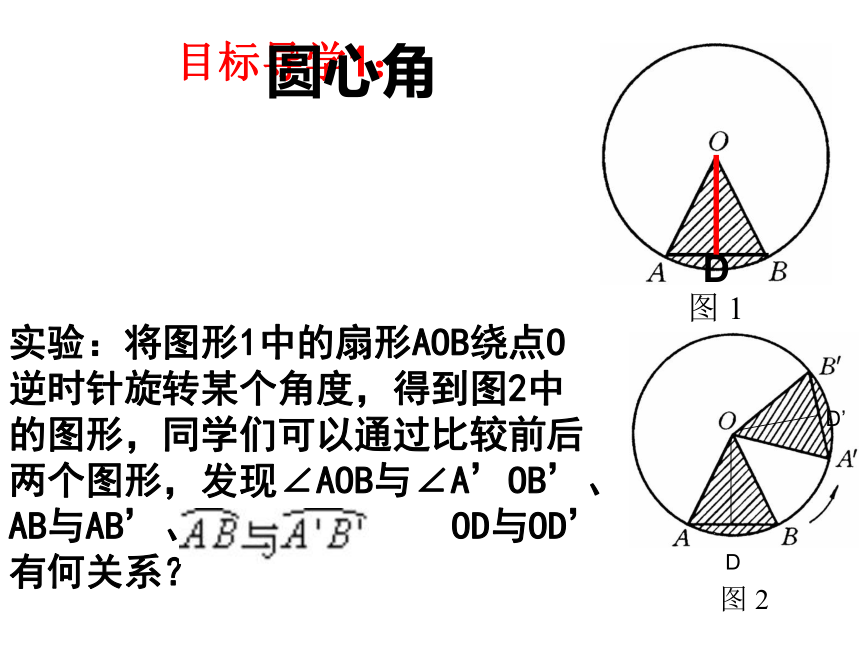
课件28张PPT。--圆心角25.2 圆的对称性(第三课时)沪科版九年级数学(下)第25章圆圆是中心对称图形吗?它的对称中心在哪里?·一、思考圆是中心对称图形,它的对称中心是圆心.· 圆心角:我们把顶点在圆心的角叫做圆心角.O二、概念如图中所示, ∠AOB就是一个圆心角。1、判别下列各图中的角是不是圆心角,并说明理由。①②③④任意给圆心角,对应出现三个量:圆心角弧弦探究:疑问:这三个量之间会有什么关系呢?目标导学1:实验:将图形1中的扇形AOB绕点O逆时针旋转某个角度,得到图2中的图形,同学们可以通过比较前后两个图形,发现∠AOB与∠A’OB’、AB与AB’、 OD与OD’ 有何关系?圆心角圆心角 顶点在圆心的角(如∠AOB).
弦心距 过圆心作弦的垂线,
圆心与垂足之间的
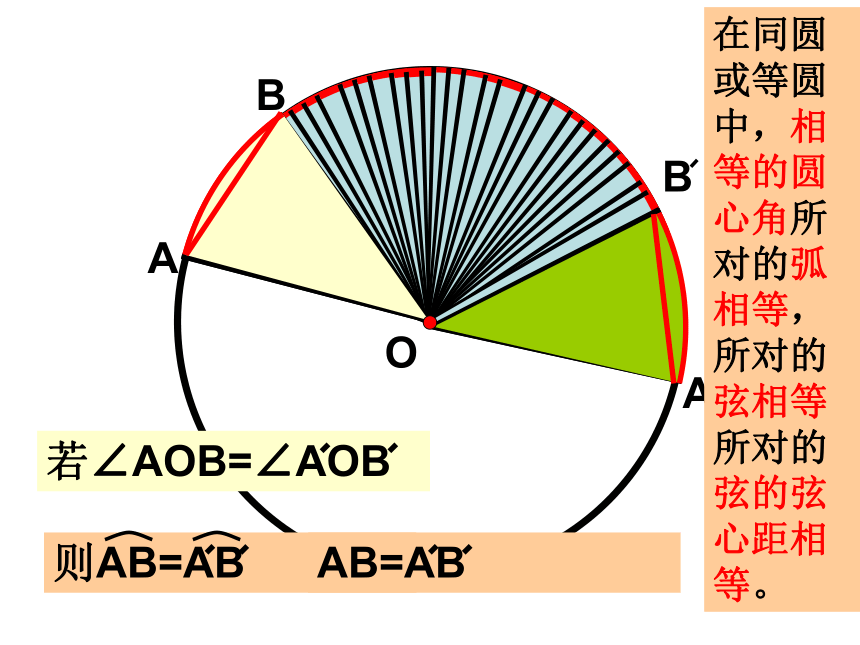
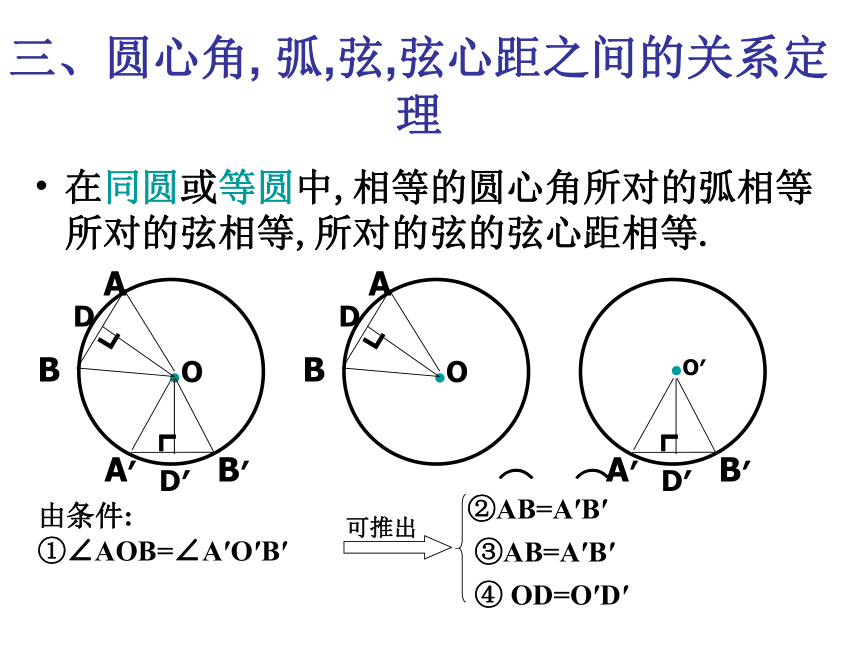
距离(如线段OD).DOAB若∠AOB=∠AOB则AB=ABAB=AB在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等所对的弦的弦心距相等。三、圆心角, 弧,弦,弦心距之间的关系定理在同圆或等圆中,相等的圆心角所对的弧相等所对的弦相等,所对的弦的弦心距相等.由条件:
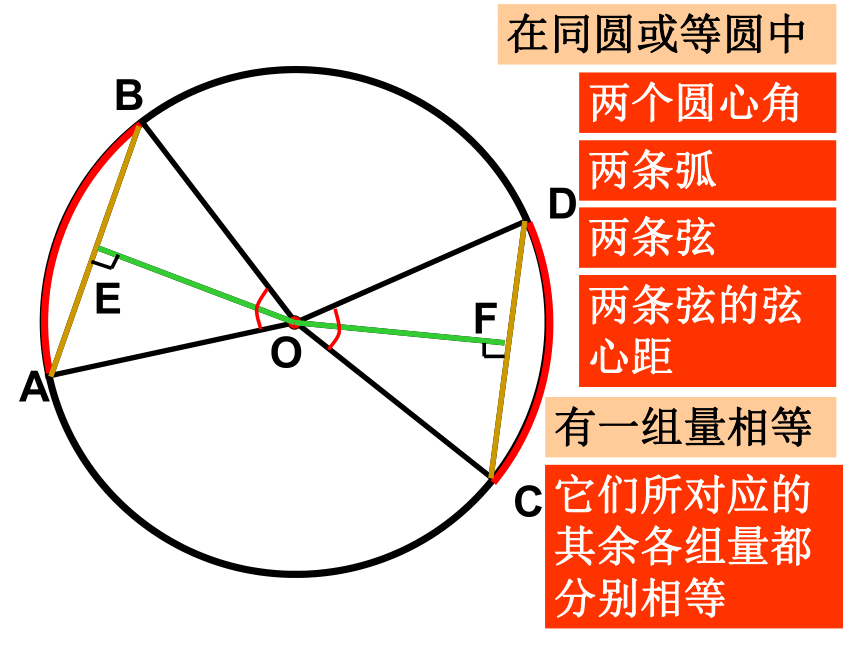
①∠AOB=∠A′O′B′③AB=A′B′④ OD=O′D′ABODCEF在同圆或等圆中两个圆心角两条弧两条弦两条弦的弦心距有一组量相等它们所对应的其余各组量都分别相等(1) 圆心角(2) 弧(3) 弦知一得三等对等定理整体理解:αABA1B1α(4) 弦心距C1COAB下面的说法正确吗?为什么?
如图,因为 根据圆心角、弧、弦的关系定理可知: ⌒⌒讨论一下!∵把圆心角等分成360份,则每一份的圆心角是1o.同时整个圆也被分成了360份.则每一份这样的弧叫做1o的弧.这样,1o的圆心角对着1o的弧,
1o的弧对着1o的圆心角.
n o的圆心角对着no的弧,
n o的弧对着no的圆心角.性质:弧的度数和它所对圆心角的度数相等.小结一.判断下列说法是否正确:
相等的圆心角所对的弧相等。( )
二.如图,⊙O中,AB=CD,
,则试一试你的能力×1.如图,AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么___________,_________________.
(2)如果 = ,那么____________,___________.
(3)如果∠AOB=∠COD,那么_____________,____________.
(4)如果OE=OF,AB=CDAB=CD练习OE=OF,OE=OF,OE=OF,AB=CD 已知:AB是⊙O的直径,M.N是AO.BO的中点。CM⊥AB,DN⊥AB,分别与圆交于C.D点。
求证:AC=BDADCNMB练习2·O证明:∴ AB=AC.又∠ACB=60°,∴ AB=BC=CA.∴ ∠AOB=∠BOC=∠AOC.·ABCO四、例题选讲例1 如图, 在⊙O中, ,∠ACB=60°,
求证∠AOB=∠BOC=∠AOC.∴ △ABC是等边三角形.例2.如图,AB是⊙O的直径, , ∠COD=35°,
求∠AOE的度数.解:试一试,做一做1、如图,AB,AC都是⊙O的弦,且∠CAB=∠CBA,求证:∠COB=∠COA证明:∵∠CAB=∠CBA(已知),∴AC=BC(等角对等边)∴∠COB=∠COA(在同一圆中,如果两条弦相等,那么两条弦所对的加以角相等)。证明:∵AB,CD是⊙O的两条直径,∴∠AOC=∠BOD。∴AC=BD,又∵BE=BD,∴AC=BE1、如图,在⊙O中,弧AB=弧AC,∠B=70°.求∠C 度数.五、你会做吗?OPABCD2:如图,P是⊙O外一点,射线PAB,PCD分别交⊙O于A、B和C、D,已知AB=CD,求证:PO平分∠BPDFE3、如图6,AD=BC,那么比较AB与CD的大小.⌒⌒4、如图7所示,CD为⊙O的弦,在CD上取
CE=DF,连结OE、OF,并延长交⊙O于点A、
B.
(1)试判断△OEF的形状,并说明理由;
(2)求证:AC=BD⌒⌒5、如图,等边△ABC的三个顶点A、B、C都在⊙O上,连接OA、OB、OC,延长AO分别交BC于点P,交BC于点D,连接BD、CD.
(1)判断四边形BDCO的形状,并说明理由;
(2)若⊙O的半径为r,求△ABC的边长⌒5、思考题已知:在以O点为圆心的两个同心圆中。大圆的弦CD交小圆于E、F,OE、OF的延长线交大圆于AB。
求证:AC=DBM34126、已知A、B是⊙O上的两点,∠AOB=120°, C是弧AB的中点,试确定四边形OACB的形状,并说明理由。7、在平行四边形ABCD中,以A为圆心,AB长为半径的圆分别交AD、BC于F、G,交BA的延长线于E,求证:EF=FG六、作业:1、课后练习2、3
2、习题25.2 第3 、 4 、 5 、 6 、 7题再见
弦心距 过圆心作弦的垂线,
圆心与垂足之间的
距离(如线段OD).DOAB若∠AOB=∠AOB则AB=ABAB=AB在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等所对的弦的弦心距相等。三、圆心角, 弧,弦,弦心距之间的关系定理在同圆或等圆中,相等的圆心角所对的弧相等所对的弦相等,所对的弦的弦心距相等.由条件:
①∠AOB=∠A′O′B′③AB=A′B′④ OD=O′D′ABODCEF在同圆或等圆中两个圆心角两条弧两条弦两条弦的弦心距有一组量相等它们所对应的其余各组量都分别相等(1) 圆心角(2) 弧(3) 弦知一得三等对等定理整体理解:αABA1B1α(4) 弦心距C1COAB下面的说法正确吗?为什么?
如图,因为 根据圆心角、弧、弦的关系定理可知: ⌒⌒讨论一下!∵把圆心角等分成360份,则每一份的圆心角是1o.同时整个圆也被分成了360份.则每一份这样的弧叫做1o的弧.这样,1o的圆心角对着1o的弧,
1o的弧对着1o的圆心角.
n o的圆心角对着no的弧,
n o的弧对着no的圆心角.性质:弧的度数和它所对圆心角的度数相等.小结一.判断下列说法是否正确:
相等的圆心角所对的弧相等。( )
二.如图,⊙O中,AB=CD,
,则试一试你的能力×1.如图,AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么___________,_________________.
(2)如果 = ,那么____________,___________.
(3)如果∠AOB=∠COD,那么_____________,____________.
(4)如果OE=OF,AB=CDAB=CD练习OE=OF,OE=OF,OE=OF,AB=CD 已知:AB是⊙O的直径,M.N是AO.BO的中点。CM⊥AB,DN⊥AB,分别与圆交于C.D点。
求证:AC=BDADCNMB练习2·O证明:∴ AB=AC.又∠ACB=60°,∴ AB=BC=CA.∴ ∠AOB=∠BOC=∠AOC.·ABCO四、例题选讲例1 如图, 在⊙O中, ,∠ACB=60°,
求证∠AOB=∠BOC=∠AOC.∴ △ABC是等边三角形.例2.如图,AB是⊙O的直径, , ∠COD=35°,
求∠AOE的度数.解:试一试,做一做1、如图,AB,AC都是⊙O的弦,且∠CAB=∠CBA,求证:∠COB=∠COA证明:∵∠CAB=∠CBA(已知),∴AC=BC(等角对等边)∴∠COB=∠COA(在同一圆中,如果两条弦相等,那么两条弦所对的加以角相等)。证明:∵AB,CD是⊙O的两条直径,∴∠AOC=∠BOD。∴AC=BD,又∵BE=BD,∴AC=BE1、如图,在⊙O中,弧AB=弧AC,∠B=70°.求∠C 度数.五、你会做吗?OPABCD2:如图,P是⊙O外一点,射线PAB,PCD分别交⊙O于A、B和C、D,已知AB=CD,求证:PO平分∠BPDFE3、如图6,AD=BC,那么比较AB与CD的大小.⌒⌒4、如图7所示,CD为⊙O的弦,在CD上取
CE=DF,连结OE、OF,并延长交⊙O于点A、
B.
(1)试判断△OEF的形状,并说明理由;
(2)求证:AC=BD⌒⌒5、如图,等边△ABC的三个顶点A、B、C都在⊙O上,连接OA、OB、OC,延长AO分别交BC于点P,交BC于点D,连接BD、CD.
(1)判断四边形BDCO的形状,并说明理由;
(2)若⊙O的半径为r,求△ABC的边长⌒5、思考题已知:在以O点为圆心的两个同心圆中。大圆的弦CD交小圆于E、F,OE、OF的延长线交大圆于AB。
求证:AC=DBM34126、已知A、B是⊙O上的两点,∠AOB=120°, C是弧AB的中点,试确定四边形OACB的形状,并说明理由。7、在平行四边形ABCD中,以A为圆心,AB长为半径的圆分别交AD、BC于F、G,交BA的延长线于E,求证:EF=FG六、作业:1、课后练习2、3
2、习题25.2 第3 、 4 、 5 、 6 、 7题再见
