5.3.1平行线的性质
图片预览




文档简介
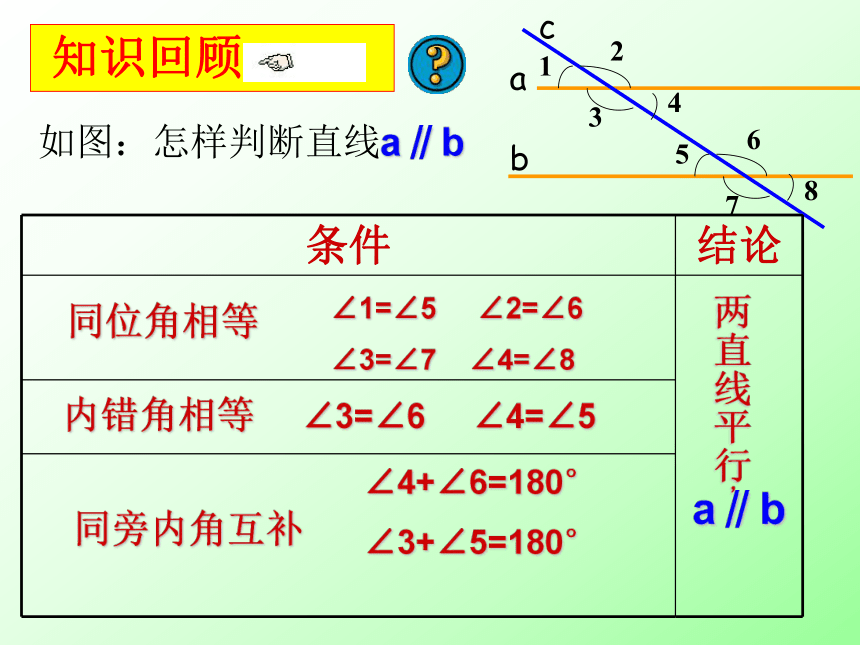
课件16张PPT。平行线性质 ∠1=∠5 ∠2=∠6
∠3=∠7 ∠4=∠8∠3=∠6 ∠4=∠5 ∠4+∠6=180°
∠3+∠5=180° a∥b 内错角相等 同旁内角互补同位角相等 知识回顾如图:怎样判断直线a∥b 两直线平行,
平行线的性质(一)
两条平行线被第三条直线所截, 同位 角相等。
简单地说:两直线平行,
同位角相等。12ACDEF书写格式: ∵ AB ∥ CD (已知)
∴ ∠1=∠2
( 两直线平行,同位角相等.)
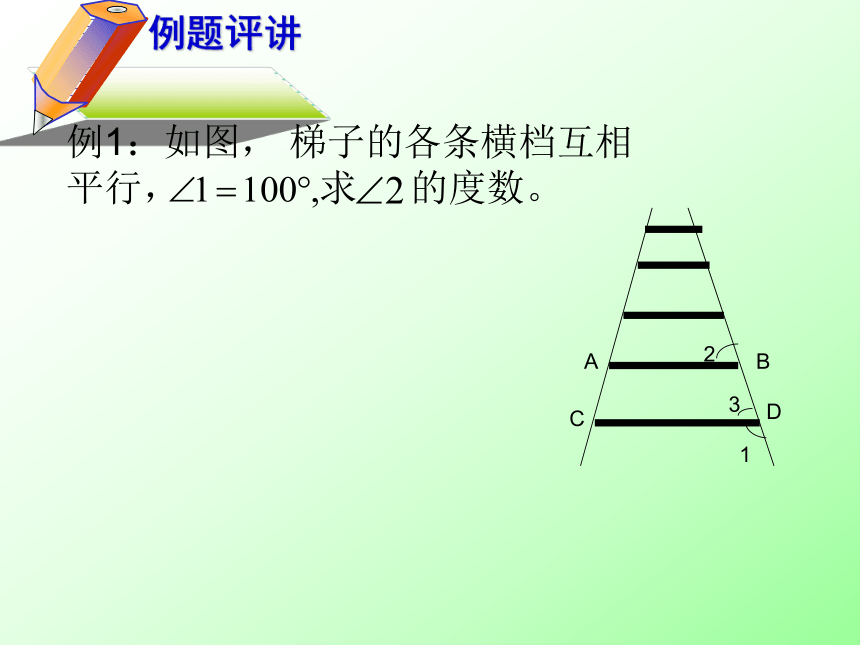
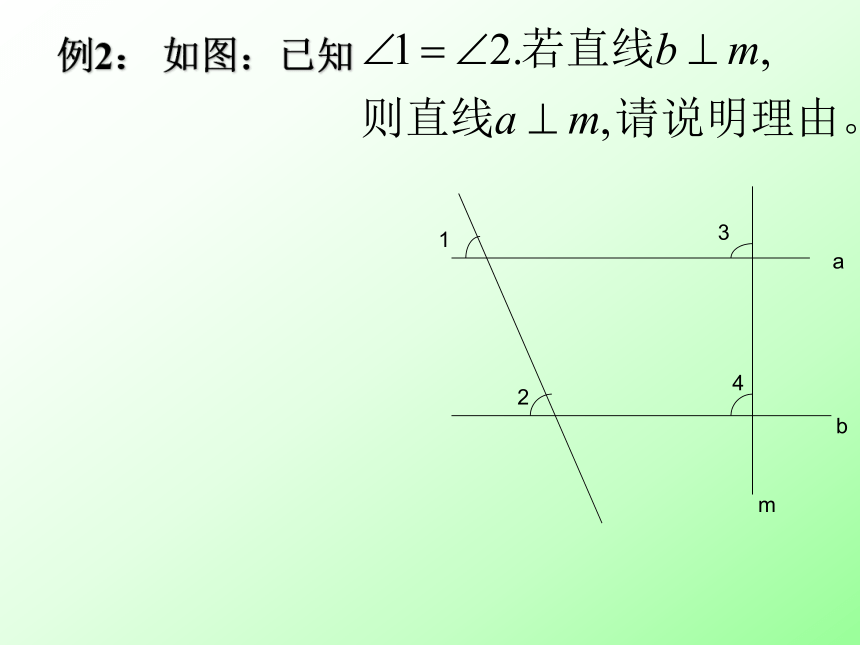
BBCD例1:如图, 梯子的各条横档互相平行, 求 的度数。ABCD231 例2: 如图:已知1234abm(1)∵∠ADE=∠B=60o(已知)
∴DE∥BC(同位角相等,两直线平行)(2)∵DE∥BC(已证)
∴∠C=∠AED=40o(两直线平行,同位角相等)解: 如图,已知D是AB上一点,E是AC上一点,∠ADE=60o,∠B=60o,∠AED=40o
(1)DE和BC平行吗?为什么?
(2)∠C是多少度?为什么?问题本节课你学到了什么? 本节课学习了平行线的性质 ,总结了平行线的判定与性质的区别.
条件:角的关系 平行关系
特征:平行关系 角的关系
本节课初步学习了如何应用平行线的识别与特征进行计算和说理(证明).
要懂得几何中的计算往往要说理,要熟悉几何里计算题的格式;
还要懂得几何中常常可以由“已知”的条件推得一系列新的结论,在这个过程中,要能清楚每一步推理的依据,并初步了解解答这类问题的格式和要求. ABCD1234EF2.两直线平行,内错角相等3.两直线平行,同旁内角互补平行线的性质:
性质1:两直线平行,同位角相等.
性质2:两直线平行,内错角相等.
性质3:两直线平行,同旁内角互补.平行线的判定同位角相等,两直线平行.内错角相等,两直线平行.同旁内角互补,两直线平行.平行线的性质两直线平行,同位角相等.两直线平行,内错角相等.两直线平行,同旁内角互补.例1:已知:直线a∥b, c∥d, ∠1=115°,
求: ∠2、∠3的度数
练一练:1234abcd如图,已知∠1=∠2,∠3=60°,求∠4的度数.例3 如图,已知AB∥CD, AD∥BC.
判断∠1与∠2是否相等.并说明理由.ABCD12例3 如图,已知AB∥CD, ∠1=∠2.
判断AD和BC是否平行.并说明理由.ABCD12例4 如图,已知∠ABC+∠C=180°,BD平分∠ABC.∠CBD与∠D相等吗?请说明理由.ABDC你会了吗?如图,已知AD∥BC,∠BAD=∠BCD.
请说明AB与CD平行的理由.ABCD
∠3=∠7 ∠4=∠8∠3=∠6 ∠4=∠5 ∠4+∠6=180°
∠3+∠5=180° a∥b 内错角相等 同旁内角互补同位角相等 知识回顾如图:怎样判断直线a∥b 两直线平行,
平行线的性质(一)
两条平行线被第三条直线所截, 同位 角相等。
简单地说:两直线平行,
同位角相等。12ACDEF书写格式: ∵ AB ∥ CD (已知)
∴ ∠1=∠2
( 两直线平行,同位角相等.)
BBCD例1:如图, 梯子的各条横档互相平行, 求 的度数。ABCD231 例2: 如图:已知1234abm(1)∵∠ADE=∠B=60o(已知)
∴DE∥BC(同位角相等,两直线平行)(2)∵DE∥BC(已证)
∴∠C=∠AED=40o(两直线平行,同位角相等)解: 如图,已知D是AB上一点,E是AC上一点,∠ADE=60o,∠B=60o,∠AED=40o
(1)DE和BC平行吗?为什么?
(2)∠C是多少度?为什么?问题本节课你学到了什么? 本节课学习了平行线的性质 ,总结了平行线的判定与性质的区别.
条件:角的关系 平行关系
特征:平行关系 角的关系
本节课初步学习了如何应用平行线的识别与特征进行计算和说理(证明).
要懂得几何中的计算往往要说理,要熟悉几何里计算题的格式;
还要懂得几何中常常可以由“已知”的条件推得一系列新的结论,在这个过程中,要能清楚每一步推理的依据,并初步了解解答这类问题的格式和要求. ABCD1234EF2.两直线平行,内错角相等3.两直线平行,同旁内角互补平行线的性质:
性质1:两直线平行,同位角相等.
性质2:两直线平行,内错角相等.
性质3:两直线平行,同旁内角互补.平行线的判定同位角相等,两直线平行.内错角相等,两直线平行.同旁内角互补,两直线平行.平行线的性质两直线平行,同位角相等.两直线平行,内错角相等.两直线平行,同旁内角互补.例1:已知:直线a∥b, c∥d, ∠1=115°,
求: ∠2、∠3的度数
练一练:1234abcd如图,已知∠1=∠2,∠3=60°,求∠4的度数.例3 如图,已知AB∥CD, AD∥BC.
判断∠1与∠2是否相等.并说明理由.ABCD12例3 如图,已知AB∥CD, ∠1=∠2.
判断AD和BC是否平行.并说明理由.ABCD12例4 如图,已知∠ABC+∠C=180°,BD平分∠ABC.∠CBD与∠D相等吗?请说明理由.ABDC你会了吗?如图,已知AD∥BC,∠BAD=∠BCD.
请说明AB与CD平行的理由.ABCD
