课题学习:图形的镶嵌[下学期]
图片预览








文档简介
课件30张PPT。小 结 S h u x u e台州市书生中学朱仁江制作章镇镇中 丁亚飞请你欣赏 用一些形状相同或不同的平面封闭图形进行拼接,彼此之间不留空隙,不重叠地铺成一片,在几何里叫图形的镶嵌,也叫图形的密铺.
图 形 的 镶 嵌小组活动一 试用平面图形纸片拼成无空隙不重叠的图案, 比一比哪个小组的方案多。结论 镶嵌成一个平面图形的条件是:
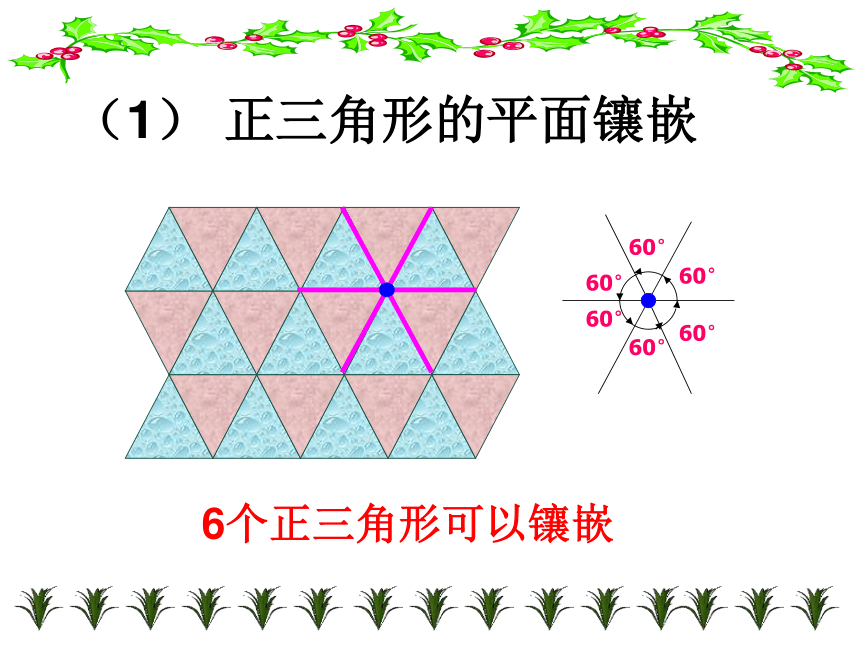
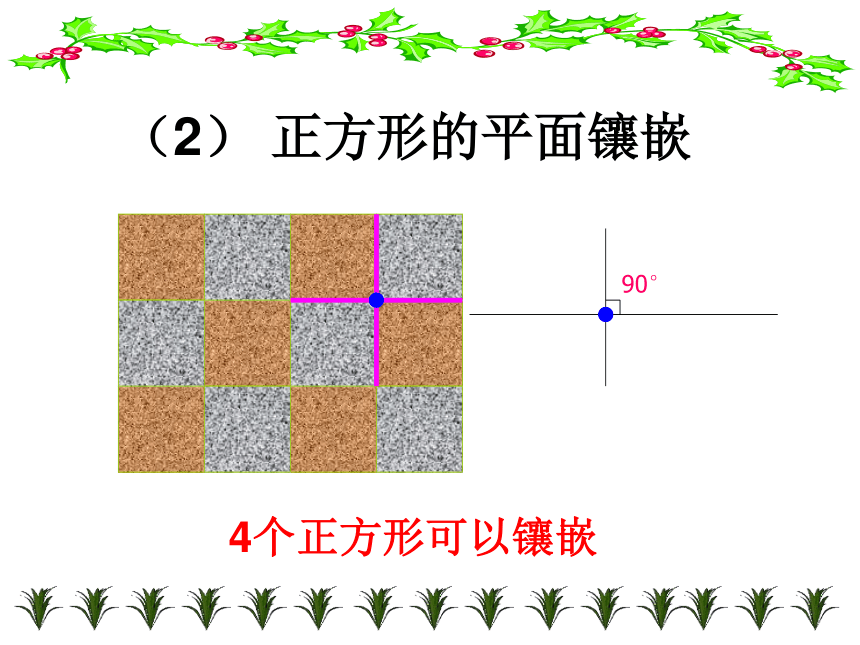
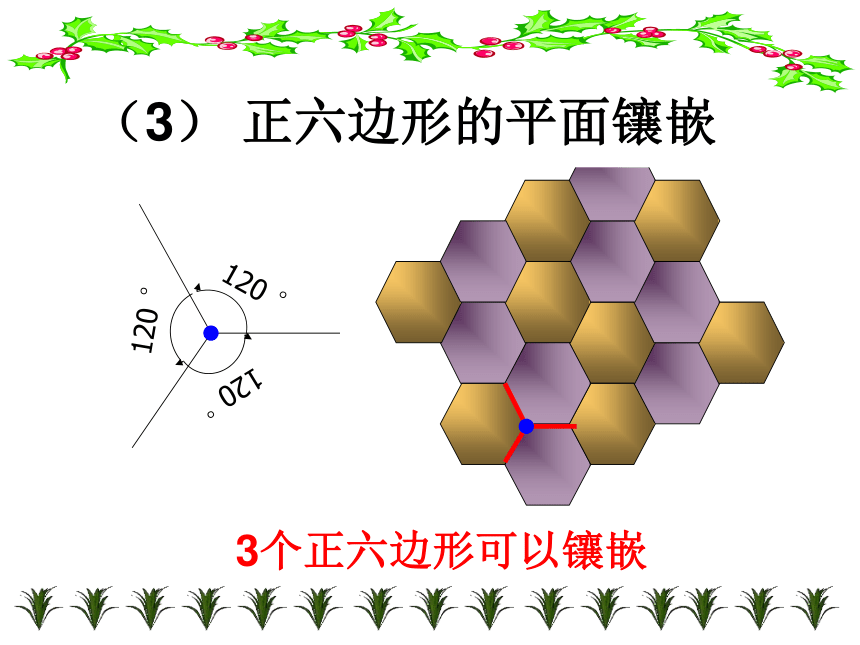
需使围绕一点拼在一起的各个多边形内角之和等于360度。60°60°60°60°60°60°6个正三角形可以镶嵌(1) 正三角形的平面镶嵌(2) 正方形的平面镶嵌90°4个正方形可以镶嵌120 °120 °120 °3个正六边形可以镶嵌(3) 正六边形的平面镶嵌注意:同一个组合会有不同的镶嵌效果①(1)正三角形与正方形图案120°120°60°60°(2)正三角形与正六边形的平面镶嵌图案(Ⅰ)(2)正三角形与正六边形的平面镶嵌图案(Ⅱ)60°60°120°60°60°每个顶点处正六边形 1 个,正三角形 4 个。1个正四边形+2个正八边形1个正三角形+2个正十二边形下列不同正多边形也能镶嵌正三角形、正方形与正六边形正方形、正六边形
与正十二边形 为什么用一种正多边形铺满地面时,只有正三角形、正方形和正六边形三种? 探究 因为要镶嵌成一个平面图形的条件是围绕一点拼在一起的各个多边形内角之和等于360度。
在正多边形里,正三角形的每个内角都是60度,正四边形的每个内角都是90度,正六边形的每个内角都是120度,这三种正多边形的一个内角的倍数都是360度。
而其他的每个内角的倍数都不是360度,所以说在正多边形里只有正三角形正四边形正六边形,可以铺满地面。探究 用两种正多边形组
合,进行镶嵌的条件。
想做一做
剪出一些形状、大小完全相同的任意三角形纸板,拼拼看,它们能否镶嵌成平面图案?请说说你的想法小组活动二 每个拼接点有6个角分别是这种三角形的内角(其中有三组分别相等),它们可以组成两个三角形的内角,其和为360度。
剪出一些形状、大小完全相同的任意四边形纸板,拼拼看,它们能否镶嵌成平面图案?请说说你的想法.
做一做小组活动二
因为在每个拼结点处,有4个角,这四个角恰好是这种四边形的内角,而四边形内角和为360度, 刚好构成一个周角,故可以镶嵌。112233433 铺 地 砖设计大赛设计一幅用平面图形铺满地面的美丽图案,与你的小伙伴比一比,看看谁设计得更有新意1 关注数学中的美 2 关注身边的数学随堂启迪课堂小结
谈谈这节课你有什么收获?本节课我们通过活动,探索出图形镶嵌的条件, 知道任意一个三角形,四边形或正六边形可以镶嵌成一个平面,并且探索出正多边形镶嵌的条件,等等。
图 形 的 镶 嵌小组活动一 试用平面图形纸片拼成无空隙不重叠的图案, 比一比哪个小组的方案多。结论 镶嵌成一个平面图形的条件是:
需使围绕一点拼在一起的各个多边形内角之和等于360度。60°60°60°60°60°60°6个正三角形可以镶嵌(1) 正三角形的平面镶嵌(2) 正方形的平面镶嵌90°4个正方形可以镶嵌120 °120 °120 °3个正六边形可以镶嵌(3) 正六边形的平面镶嵌注意:同一个组合会有不同的镶嵌效果①(1)正三角形与正方形图案120°120°60°60°(2)正三角形与正六边形的平面镶嵌图案(Ⅰ)(2)正三角形与正六边形的平面镶嵌图案(Ⅱ)60°60°120°60°60°每个顶点处正六边形 1 个,正三角形 4 个。1个正四边形+2个正八边形1个正三角形+2个正十二边形下列不同正多边形也能镶嵌正三角形、正方形与正六边形正方形、正六边形
与正十二边形 为什么用一种正多边形铺满地面时,只有正三角形、正方形和正六边形三种? 探究 因为要镶嵌成一个平面图形的条件是围绕一点拼在一起的各个多边形内角之和等于360度。
在正多边形里,正三角形的每个内角都是60度,正四边形的每个内角都是90度,正六边形的每个内角都是120度,这三种正多边形的一个内角的倍数都是360度。
而其他的每个内角的倍数都不是360度,所以说在正多边形里只有正三角形正四边形正六边形,可以铺满地面。探究 用两种正多边形组
合,进行镶嵌的条件。
想做一做
剪出一些形状、大小完全相同的任意三角形纸板,拼拼看,它们能否镶嵌成平面图案?请说说你的想法小组活动二 每个拼接点有6个角分别是这种三角形的内角(其中有三组分别相等),它们可以组成两个三角形的内角,其和为360度。
剪出一些形状、大小完全相同的任意四边形纸板,拼拼看,它们能否镶嵌成平面图案?请说说你的想法.
做一做小组活动二
因为在每个拼结点处,有4个角,这四个角恰好是这种四边形的内角,而四边形内角和为360度, 刚好构成一个周角,故可以镶嵌。112233433 铺 地 砖设计大赛设计一幅用平面图形铺满地面的美丽图案,与你的小伙伴比一比,看看谁设计得更有新意1 关注数学中的美 2 关注身边的数学随堂启迪课堂小结
谈谈这节课你有什么收获?本节课我们通过活动,探索出图形镶嵌的条件, 知道任意一个三角形,四边形或正六边形可以镶嵌成一个平面,并且探索出正多边形镶嵌的条件,等等。
