第八单元 第3课时 田忌赛马(课件)四年级数学上册 人教版(共28张PPT)
文档属性
| 名称 | 第八单元 第3课时 田忌赛马(课件)四年级数学上册 人教版(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 22.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 00:00:00 | ||
图片预览




文档简介
(共28张PPT)
人教版四年级数学上册
8
数学广角—优化
第3课时 田忌赛马问题
同学们听过“田忌赛马”的故事吗?
点击播放视频
胜
齐王
田忌
胜
胜
3
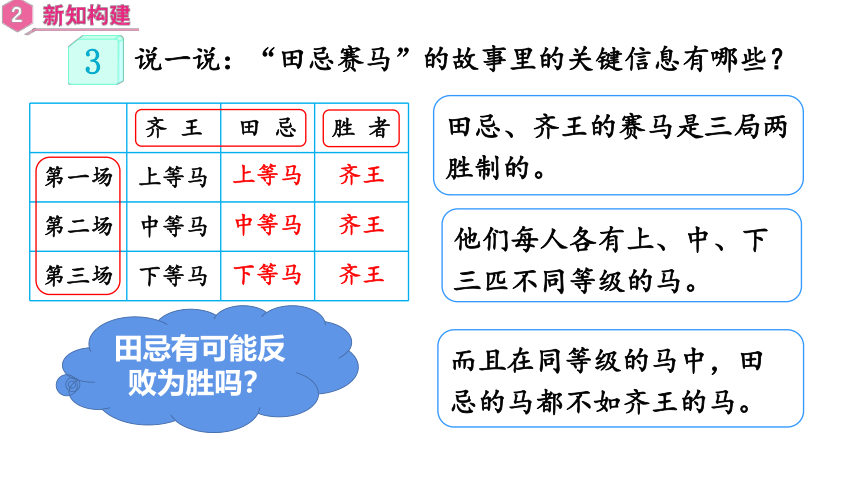
说一说:“田忌赛马”的故事里的关键信息有哪些?
田忌、齐王的赛马是三局两胜制的。
他们每人各有上、中、下三匹不同等级的马。
而且在同等级的马中,田忌的马都不如齐王的马。
齐 王 田 忌 胜 者
第一场 上等马
第二场 中等马
第三场 下等马
上等马
中等马
下等马
齐王
齐王
齐王
三局两胜,齐王胜
田忌有可能反败为胜吗?
胜
齐王
田忌
胜
胜
3
田忌是怎样赢了齐王的?
让我们先来看看三场赛马的比赛情况吧。
齐 王 田 忌 本场胜者
第一场 上等马
第二场 中等马
第三场 下等马
下等马
上等马
中等马
齐王
田忌
田忌
3
田忌是怎样赢了齐王的?
三局两胜,田忌胜
我们可以把两人赛马的情况用表格表示出来。
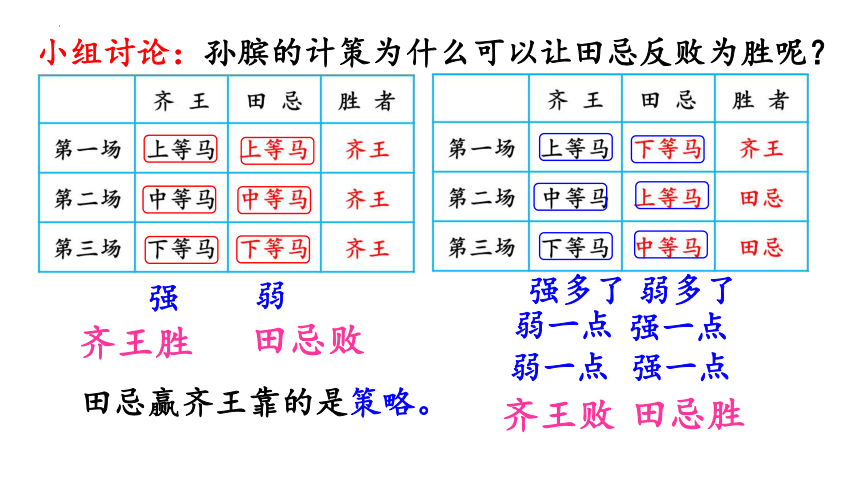
小组讨论:孙膑的计策为什么可以让田忌反败为胜呢?
弱
强
田忌败
齐王胜
弱多了
强多了
强一点
弱一点
强一点
弱一点
齐王败
田忌胜
田忌赢齐王靠的是策略。
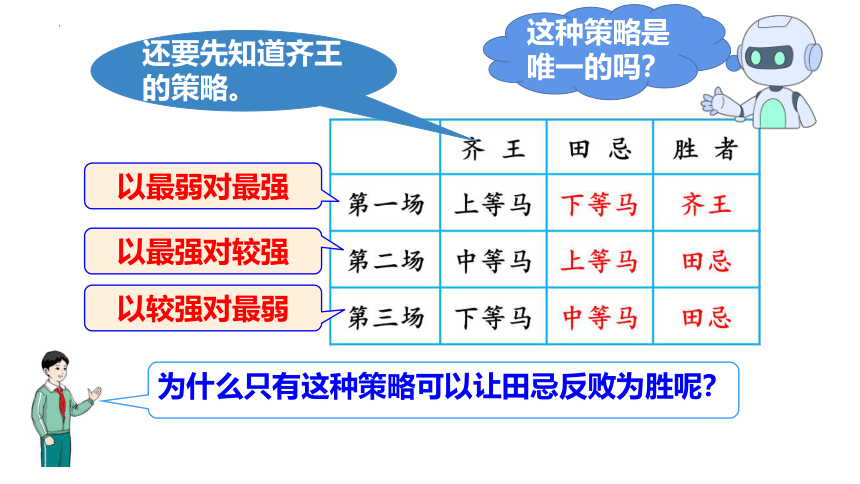
以最弱对最强
以最强对较强
以较强对最弱
还要先知道齐王的策略。
为什么只有这种策略可以让田忌反败为胜呢?
这种策略是唯一的吗?
对阵方 第一场 第二场 第三场 获胜方
齐 王 上等马 中等马 下等马
田忌1
田忌2
田忌3
田忌4
田忌5
田忌6
上等马
中等马
下等马
齐王
上等马
下等马
中等马
齐王
中等马
上等马
下等马
中等马
下等马
上等马
齐王
齐王
下等马
上等马
中等马
田忌
下等马
中等马
上等马
齐王
可以用排列组合的方法列出应对策略。
我们来看看田忌共有多少种可采用的应对策略。
仔细观察这张表格,你发现了什么?
一共有6种策略,只有1种田忌获胜。
对阵方 第一场 第二场 第三场 获胜方
齐 王 上等马 中等马 下等马
田忌1
田忌2
田忌3
田忌4
田忌5
田忌6
上等马
中等马
下等马
齐王
上等马
下等马
中等马
齐王
中等马
上等马
下等马
中等马
下等马
上等马
齐王
齐王
下等马
上等马
中等马
田忌
下等马
中等马
上等马
齐王
想一想,说一说:在田忌赛马中,我们是如何思考的?
因为田忌的下等马谁都赢不了,所以我们让下等马对齐王最强的上等马。浪费掉了齐王的优势。
接下来的两匹马将稳赢。
田忌获胜的前提也必须是齐王先派马。
在决定策略中,对方的信息是很重要的。
归纳小结
把解决问题的所有可能性都一一找出来,然后从中找到最优策略,这是数学中一种很重要的方法。
怎样寻找最优策略呢?
1.解决同一个问题可以有不同的策略,要学会寻找解决问题 的最优方案。
2.在与对方进行比赛时:
(1)要知己知彼,详细地分析双方的情况。
(2)想到所有可能的对策。
(3)选择一个利多弊少的最优策略。
1.
两人玩扑克牌比大小的游戏,每人每次出一张牌,各出3次,赢两次者胜。
可以用列表法列举所有情形。
小红拿的是右边下面一组的牌,她有可能获胜吗?
教科书第106页“做一做”
做一做
三局两胜
小红保证有两次出的卡片比上面大就能获胜。
第一次 第二次 第三次 获胜方
对方 9 7 5
小红1
小红2
小红3
小红4
小红5
小红6
8
6
3
对方
8
3
6
6
8
3
6
3
8
对方
3
8
6
小红
3
6
8
对方
答:有可能。让对方先出牌,用最小的牌对对方最大的牌,使对方最大的牌发挥最小的作用,才能获胜。
对方
对方
也可以利用“田忌赛马”策略直接列表解答。
小 红
小 红
小 红
对 方 小 红 本场胜者
第一次
第二次
第三次
小 红
9
3
7
8
5
6
对 方
2.如果比赛中每个人都发挥正常,第2队怎样布阵才能获胜?(教材P107练习二十第3题)
对阵五次,至少有三次胜了才算赢。
第2队以最弱的2人对阵第1队最强的2人,剩的3人均以强的对阵对方弱的,就可以胜三局。
思路分析:“五局三胜”,即五局中只要胜三局就可以获胜。所以只要第 2 队三胜二负或三胜一负一平都可取胜。根据双方队员的成绩,利用“田忌赛马”策略安排比赛顺序即可。
2.
教科书第107页第3题
陆 莎
朱 曼
第1队
赵天骁
刘佳佳
第1队
陶欣然
宋圆圆
第2队
杜小雯
肖 刚
第2队
程 刚
何文龙
第2队
方案一
2.
教科书第107页第3题
陆 莎
朱 曼
第1队
赵天骁
宋圆圆
-
陶欣然
肖 刚
第2队
杜小雯
何文龙
第2队
程 刚
刘佳佳
第2队
方案二
3. 有20颗豆,甲、乙两人轮流取走,每次只能取1颗或2颗,谁取到最后一颗豆谁就赢。想一想,获胜策略是什么?
根据规则:甲、乙两人轮
流取走,每次只能取1颗
或2颗。可以先从3颗豆开
始试一试。
3颗豆获胜策略:3÷3=1
(1)让对方先取;
(2)对方取1,自己就取2,对方取2,自己就取1。
4颗豆获胜策略:
(1)自己先取1;
(2)剩下3。对方取1,自己就取2,对方取2,自己就取1。
如果是4颗豆、5颗豆、6颗豆呢?
4÷3=1……1
5颗豆获胜策略:
5÷3=1……2
(1)自己先取2;
(2)剩下3。对方取1,自己就取2,对方取2,
自己就取1。
6颗豆获胜策略:6÷3=2
(1)让对方先取;
(2)对方取1,自己就取2,对方取2,自己就取1。
获胜策略:
豆的总数
÷
每个回合
最多总颗数
有余数
我方先取余数
没有余数
让对方先取
3.有20颗豆,甲、乙两人轮流取走,每次只能取1颗或2颗,谁取到最后一颗豆谁就赢。想一想,获胜策略是什么?
保证每个回合两人取豆颗数的和为3。
有20颗豆,要想最终获胜,选择自己先取豆,还是让对手先取豆呢?
20÷3=6……2
答:自己先取2颗。
两人轮流报数,每次只能报1或2,把两人报的所有数加起来,谁报数后和是10,谁获胜。
数学游戏
如果让你先报数,为了确保获胜,你第一次应该报几?接下来应该怎么报?
4.
思路分析:每次只能报1或2,要想两人报的所有数的和为10,则要想办法最后留下3给对方,而10里有3个3还余1,故第一次应该报1。接下来对方报1, 我报2; 对方报2, 我报1, 就能确保获胜。
两人轮流报数,每次只能报1或2,把两人报的所有数加起来,谁报数后和是10,谁获胜。
数学游戏
如果让你先报数,为了确保获胜,你第一次应该报几?接下来应该怎么报?
4.
答:为了确保获胜,第一次应该报1,接下来对方报1, 我报2; 对方报2, 我报1, 保证每个回合两人报数之和为3,这样你就能确保胜利。
1+2=3
10÷3=3……1
思路分析:每次只能取1根或2根,则一次两人取走火柴根数的和最多是3, 15里面刚好5个3,没有余数,所以让对方先取,对方取1,我取2;对方取2,我取1,就能保证最后一根被我取走。
5. 有15根火柴,A、B两人轮流取走,每次只能取1根或2根,谁取到最后一根火柴谁就赢。想一想,为了确保获胜,是应该先取,还是应该后取?怎样取?
正确解答:15÷(1+2)=5(次)
答:为了确保获胜,应该后取。对方取1根, 我取2根; 对方取2根, 我取1根。这样就能取到最后一根火柴。
5. 有15根火柴,A、B两人轮流取走,每次只能取1根或2根,谁取到最后一根火柴谁就赢。想一想,为了确保获胜,是应该先取,还是应该后取?怎样取?
“当取(或数)到最后一个赢”的解题策略:
(1)找周期:周期等于可以取(或数)的最大数+最小数;
(3)总数除以周期,没有余数时,后取,跟随对方,与之组成一个周期的数。
(2)总数除以周期,有余数时,先取(或数),取(或数)走余数;
通用方法
1.解决同一问题可以有不同的策略,要学会寻找解决问题的最优策略。
2.在与对方进行比赛时,要详细地分析自己与对方的情况,反复研究各种策略,在所有可能采用的策略中,选择一个利多弊少的最优策略,从而使劣势变为优势,最终获得胜利。
这节课你有什么收获?
人教版四年级数学上册
8
数学广角—优化
第3课时 田忌赛马问题
同学们听过“田忌赛马”的故事吗?
点击播放视频
胜
齐王
田忌
胜
胜
3
说一说:“田忌赛马”的故事里的关键信息有哪些?
田忌、齐王的赛马是三局两胜制的。
他们每人各有上、中、下三匹不同等级的马。
而且在同等级的马中,田忌的马都不如齐王的马。
齐 王 田 忌 胜 者
第一场 上等马
第二场 中等马
第三场 下等马
上等马
中等马
下等马
齐王
齐王
齐王
三局两胜,齐王胜
田忌有可能反败为胜吗?
胜
齐王
田忌
胜
胜
3
田忌是怎样赢了齐王的?
让我们先来看看三场赛马的比赛情况吧。
齐 王 田 忌 本场胜者
第一场 上等马
第二场 中等马
第三场 下等马
下等马
上等马
中等马
齐王
田忌
田忌
3
田忌是怎样赢了齐王的?
三局两胜,田忌胜
我们可以把两人赛马的情况用表格表示出来。
小组讨论:孙膑的计策为什么可以让田忌反败为胜呢?
弱
强
田忌败
齐王胜
弱多了
强多了
强一点
弱一点
强一点
弱一点
齐王败
田忌胜
田忌赢齐王靠的是策略。
以最弱对最强
以最强对较强
以较强对最弱
还要先知道齐王的策略。
为什么只有这种策略可以让田忌反败为胜呢?
这种策略是唯一的吗?
对阵方 第一场 第二场 第三场 获胜方
齐 王 上等马 中等马 下等马
田忌1
田忌2
田忌3
田忌4
田忌5
田忌6
上等马
中等马
下等马
齐王
上等马
下等马
中等马
齐王
中等马
上等马
下等马
中等马
下等马
上等马
齐王
齐王
下等马
上等马
中等马
田忌
下等马
中等马
上等马
齐王
可以用排列组合的方法列出应对策略。
我们来看看田忌共有多少种可采用的应对策略。
仔细观察这张表格,你发现了什么?
一共有6种策略,只有1种田忌获胜。
对阵方 第一场 第二场 第三场 获胜方
齐 王 上等马 中等马 下等马
田忌1
田忌2
田忌3
田忌4
田忌5
田忌6
上等马
中等马
下等马
齐王
上等马
下等马
中等马
齐王
中等马
上等马
下等马
中等马
下等马
上等马
齐王
齐王
下等马
上等马
中等马
田忌
下等马
中等马
上等马
齐王
想一想,说一说:在田忌赛马中,我们是如何思考的?
因为田忌的下等马谁都赢不了,所以我们让下等马对齐王最强的上等马。浪费掉了齐王的优势。
接下来的两匹马将稳赢。
田忌获胜的前提也必须是齐王先派马。
在决定策略中,对方的信息是很重要的。
归纳小结
把解决问题的所有可能性都一一找出来,然后从中找到最优策略,这是数学中一种很重要的方法。
怎样寻找最优策略呢?
1.解决同一个问题可以有不同的策略,要学会寻找解决问题 的最优方案。
2.在与对方进行比赛时:
(1)要知己知彼,详细地分析双方的情况。
(2)想到所有可能的对策。
(3)选择一个利多弊少的最优策略。
1.
两人玩扑克牌比大小的游戏,每人每次出一张牌,各出3次,赢两次者胜。
可以用列表法列举所有情形。
小红拿的是右边下面一组的牌,她有可能获胜吗?
教科书第106页“做一做”
做一做
三局两胜
小红保证有两次出的卡片比上面大就能获胜。
第一次 第二次 第三次 获胜方
对方 9 7 5
小红1
小红2
小红3
小红4
小红5
小红6
8
6
3
对方
8
3
6
6
8
3
6
3
8
对方
3
8
6
小红
3
6
8
对方
答:有可能。让对方先出牌,用最小的牌对对方最大的牌,使对方最大的牌发挥最小的作用,才能获胜。
对方
对方
也可以利用“田忌赛马”策略直接列表解答。
小 红
小 红
小 红
对 方 小 红 本场胜者
第一次
第二次
第三次
小 红
9
3
7
8
5
6
对 方
2.如果比赛中每个人都发挥正常,第2队怎样布阵才能获胜?(教材P107练习二十第3题)
对阵五次,至少有三次胜了才算赢。
第2队以最弱的2人对阵第1队最强的2人,剩的3人均以强的对阵对方弱的,就可以胜三局。
思路分析:“五局三胜”,即五局中只要胜三局就可以获胜。所以只要第 2 队三胜二负或三胜一负一平都可取胜。根据双方队员的成绩,利用“田忌赛马”策略安排比赛顺序即可。
2.
教科书第107页第3题
陆 莎
朱 曼
第1队
赵天骁
刘佳佳
第1队
陶欣然
宋圆圆
第2队
杜小雯
肖 刚
第2队
程 刚
何文龙
第2队
方案一
2.
教科书第107页第3题
陆 莎
朱 曼
第1队
赵天骁
宋圆圆
-
陶欣然
肖 刚
第2队
杜小雯
何文龙
第2队
程 刚
刘佳佳
第2队
方案二
3. 有20颗豆,甲、乙两人轮流取走,每次只能取1颗或2颗,谁取到最后一颗豆谁就赢。想一想,获胜策略是什么?
根据规则:甲、乙两人轮
流取走,每次只能取1颗
或2颗。可以先从3颗豆开
始试一试。
3颗豆获胜策略:3÷3=1
(1)让对方先取;
(2)对方取1,自己就取2,对方取2,自己就取1。
4颗豆获胜策略:
(1)自己先取1;
(2)剩下3。对方取1,自己就取2,对方取2,自己就取1。
如果是4颗豆、5颗豆、6颗豆呢?
4÷3=1……1
5颗豆获胜策略:
5÷3=1……2
(1)自己先取2;
(2)剩下3。对方取1,自己就取2,对方取2,
自己就取1。
6颗豆获胜策略:6÷3=2
(1)让对方先取;
(2)对方取1,自己就取2,对方取2,自己就取1。
获胜策略:
豆的总数
÷
每个回合
最多总颗数
有余数
我方先取余数
没有余数
让对方先取
3.有20颗豆,甲、乙两人轮流取走,每次只能取1颗或2颗,谁取到最后一颗豆谁就赢。想一想,获胜策略是什么?
保证每个回合两人取豆颗数的和为3。
有20颗豆,要想最终获胜,选择自己先取豆,还是让对手先取豆呢?
20÷3=6……2
答:自己先取2颗。
两人轮流报数,每次只能报1或2,把两人报的所有数加起来,谁报数后和是10,谁获胜。
数学游戏
如果让你先报数,为了确保获胜,你第一次应该报几?接下来应该怎么报?
4.
思路分析:每次只能报1或2,要想两人报的所有数的和为10,则要想办法最后留下3给对方,而10里有3个3还余1,故第一次应该报1。接下来对方报1, 我报2; 对方报2, 我报1, 就能确保获胜。
两人轮流报数,每次只能报1或2,把两人报的所有数加起来,谁报数后和是10,谁获胜。
数学游戏
如果让你先报数,为了确保获胜,你第一次应该报几?接下来应该怎么报?
4.
答:为了确保获胜,第一次应该报1,接下来对方报1, 我报2; 对方报2, 我报1, 保证每个回合两人报数之和为3,这样你就能确保胜利。
1+2=3
10÷3=3……1
思路分析:每次只能取1根或2根,则一次两人取走火柴根数的和最多是3, 15里面刚好5个3,没有余数,所以让对方先取,对方取1,我取2;对方取2,我取1,就能保证最后一根被我取走。
5. 有15根火柴,A、B两人轮流取走,每次只能取1根或2根,谁取到最后一根火柴谁就赢。想一想,为了确保获胜,是应该先取,还是应该后取?怎样取?
正确解答:15÷(1+2)=5(次)
答:为了确保获胜,应该后取。对方取1根, 我取2根; 对方取2根, 我取1根。这样就能取到最后一根火柴。
5. 有15根火柴,A、B两人轮流取走,每次只能取1根或2根,谁取到最后一根火柴谁就赢。想一想,为了确保获胜,是应该先取,还是应该后取?怎样取?
“当取(或数)到最后一个赢”的解题策略:
(1)找周期:周期等于可以取(或数)的最大数+最小数;
(3)总数除以周期,没有余数时,后取,跟随对方,与之组成一个周期的数。
(2)总数除以周期,有余数时,先取(或数),取(或数)走余数;
通用方法
1.解决同一问题可以有不同的策略,要学会寻找解决问题的最优策略。
2.在与对方进行比赛时,要详细地分析自己与对方的情况,反复研究各种策略,在所有可能采用的策略中,选择一个利多弊少的最优策略,从而使劣势变为优势,最终获得胜利。
这节课你有什么收获?
