人教B版(2019)高中数学选择性必修第一册 《1.2空间中点、直线与空间向量》名师课件(共27张PPT)
文档属性
| 名称 | 人教B版(2019)高中数学选择性必修第一册 《1.2空间中点、直线与空间向量》名师课件(共27张PPT) | 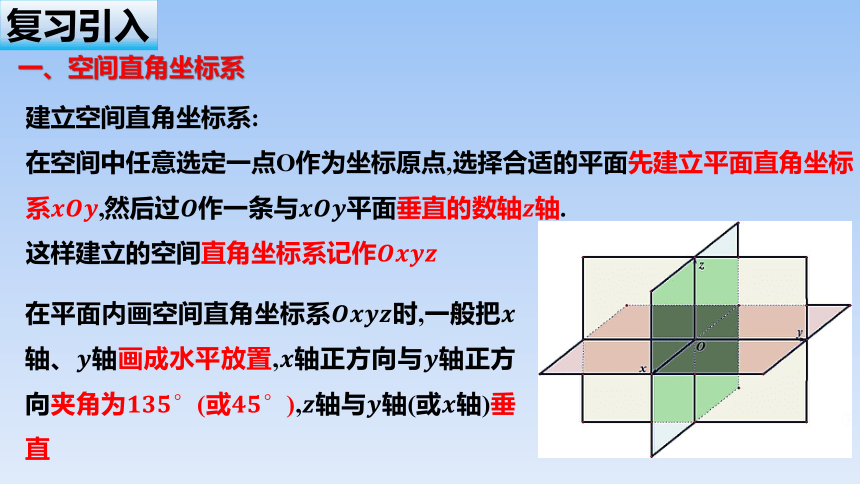 | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 22:54:00 | ||
图片预览








文档简介
(共27张PPT)
复习引入
一、空间直角坐标系
建立空间直角坐标系:
在空间中任意选定一点O作为坐标原点,选择合适的平面先建立平面直角坐标系,然后过作一条与平面垂直的数轴轴.
这样建立的空间直角坐标系记作
在平面内画空间直角坐标系时,一般把轴、轴画成水平放置,轴正方向与轴正方向夹角为(或),轴与轴(或轴)垂直
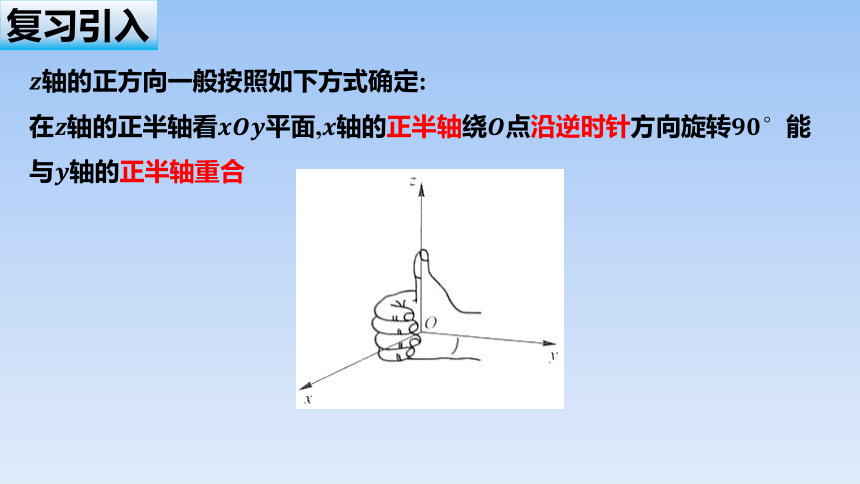
轴的正方向一般按照如下方式确定:
在轴的正半轴看平面,轴的正半轴绕点沿逆时针方向旋转能与轴的正半轴重合
复习引入
二、空间向量坐标的应用
复习引入
空间向量在空间直角坐标系中的坐标,等于表示这个空间向量的有向线段的终点坐标减去始点坐标
空间直角坐标系中两点之间的距离公式
空间直角坐标系中的中点坐标公式
人教B版同步教材名师课件
空间中的点、直线与空间向量
学习目标
学 习 目 标 核心素养
了解空间中的点与空间向量 数学抽象
了解空间中的直线与空间向量 数学抽象
掌握空间中直线平行与空间向量的关系 逻辑推理
学习目标
1.掌握直线的方向向量与直线的位置关系(重点)
2.能用平行直线的方向向量的位置关系解决实际问题(难点)
探究新知
思考:怎样确定空间中一个点的位置
空间中要确定一个点,必须是在个参照系中进行,这就是空间直角坐标系.这样可以通过点的位置向量进行确定.
问题1:(1)如图所示的四面体中,怎样借助空间向量来描述在空间中是不同的点
一、空间中的点与空间向量
可以借助向量的不同,描述在空间中是不同的点
探究新知
一般地,如果在空间中指定一点,那么空间中任意一点的位置,都可以由向量唯一确定,此时,通常称为点的位置向量.
特别地,空间直角坐标系中的任意一点都由它的位置向量唯一确定,从而也就由它的坐标唯一确定.
(2) 怎样借助空间向量来刻画空间中点的位置
探究新知
问题2:(1)如图所示的长方体中,设,如果只借助,能不能确定直线在空间中的位置
(2)一般地,怎样借助空间向量来刻画空间中直线的位置
结论:一般地,如果是空间中的一条直线,是空间中的一个非零向量,且表示的有向线段所在的直线与平行或重合,则称为直线的一个方向向量.此时,也称向量与直线平行,记作
二、空间中的直线与空间向量
探究新知
(1)如果,是直线上两个不同的点,则就是直线的一个方向向量
(2)如果是直线的一个方向向量,则对任意的实数,空间向量也是直线的一个方向向量,而且直线的任意两个方向向量都平行.
(3)如果是直线的一个方向向量,是直线的一个方向向量,则,或与重合.
注意:
(3)可用来判断两条直线是否平行.
向量可以描述所有与直线平行或重合的直线
只借助向量能否确定直线在空间中的位置
如图,因为,所以只借助向量不能确定直线在空间中的位置.
那要怎样确定直线在空间中的位置呢 需要增加什么条件呢
如果为直线的一个方向向量,为直线上一个已知的点,则对于直线上任意一点,向量一定与非零向量平行,从而可知存在唯一的实数,使得,这就是说,空间中直线的位置可由和点唯一确定.
探究新知
空间直线的向量参数方程
1.给定一个定点和一个向量,再任给一个实数,以为起点作向量.①
如图所示当变化时,点的轨迹形成直线,向量方程①称为直线以为参数的参数方程,向量称为该直线的方向向量,如图所示
探究新知
2.对空间任一个确定的点(如图所示),点在直线上的充要条件是存在唯一的实数,满足等式 ②
探究新知
如果在上取,则②式可化为,即.③
①或②或③三个向量等式都叫空间直线的向量参数方程
探究新知
注意:
直线的向量参数方程③有时也可表示为
.④
方程③和④可以用于判定三点共线.
即若或,
则三点共线,反之亦成立.
探究新知
点在平面内的充要条件
1.由共面向量定理,我们还可得到:
如果三点不共线,则点在平面内的充要条件是存在一对实数,使向量表达式成立
2.对于空间任意一点,有,这也是点在平面内的充要条件.
典例讲解
例1.已知正方体中,为的中点,
求证:直线与直线不平行.
证明:
以为原点,的方向分别为轴、轴、轴正方向,正方体的棱长为单位长度,建立如图所示的空间直角坐标系,则
所以,
又因为,所以与不平行.
因为为直线的一个方向向量, 为直线的一个方向向量,当∥ 时,必有∥ .
由上可知直线与直线不平行.
典例讲解
例2.(1)若在直线上,则直线的一个方向向量为( )
典例讲解
(2)直线的方向向量为,平面内两共点向量,下列关系中能表示的是( )
D.以上均不能
解析:
(1) ,而与共线的非零向量都可以作为直线的方向向量.答案: A
(2) 显然不能,而能表示或.答案:D
变式训练
1.已知点,为线段上一点且,则点的坐标为( )
解析:
设,∵为线段上一点且
∴,即
答案:C
2.已知正方体,点,分别是面对角线与面对角线的中点.求证:∥侧面, ∥,并且.
变式训练
解析:
如图,设,则,因此.
因为不在平面内,所以∥平面.
又因为,所以,
因此
对直线的方向向量的理解:
(1)非零性:直线的方向向量是非零向量
(2)不唯一性:直线的方向向量有无数个,可以分为方向相同和相反两类,它们都是共线向量
(3)给定空间中的任一点和非零向量,就可以确定唯一一条过点且平行于向量的直线
素养提炼
素养提炼
注意区分直线平行与向量平行的不同:
两直线平行时,其方向向量一定平行;但两直线的方向向量平行时,两直线平行或重合,切勿混淆直线与直线平行和向量与向量平行的含义
当堂练习
1.已知线段的两端点的坐标为,则线段与哪个坐标平面平行( )
或
解析:由题可知.答案:C
2.从点沿向量的方向取线段长,则点的坐标为( )
解析:设,由题可知,从而,由此列出方程,将各选项代入求解.答案:
当堂练习
3.已知分别是直线的方向向量,若,则( )
解析:由题可知,从而
答案:D
当堂练习
4.已知,点,在平面内,则_________.
解析:∴点在平面内,∴存在实数,使,即,∴
解得,
即.答案:11
归纳小结
空间中的点、直线与空间向量
用空间向量表示空间中的点
用空间向量表示直线
用向量证明平行关系
作 业
教材P36页练习A第1,2,4,5题
练习B第2题
复习引入
一、空间直角坐标系
建立空间直角坐标系:
在空间中任意选定一点O作为坐标原点,选择合适的平面先建立平面直角坐标系,然后过作一条与平面垂直的数轴轴.
这样建立的空间直角坐标系记作
在平面内画空间直角坐标系时,一般把轴、轴画成水平放置,轴正方向与轴正方向夹角为(或),轴与轴(或轴)垂直
轴的正方向一般按照如下方式确定:
在轴的正半轴看平面,轴的正半轴绕点沿逆时针方向旋转能与轴的正半轴重合
复习引入
二、空间向量坐标的应用
复习引入
空间向量在空间直角坐标系中的坐标,等于表示这个空间向量的有向线段的终点坐标减去始点坐标
空间直角坐标系中两点之间的距离公式
空间直角坐标系中的中点坐标公式
人教B版同步教材名师课件
空间中的点、直线与空间向量
学习目标
学 习 目 标 核心素养
了解空间中的点与空间向量 数学抽象
了解空间中的直线与空间向量 数学抽象
掌握空间中直线平行与空间向量的关系 逻辑推理
学习目标
1.掌握直线的方向向量与直线的位置关系(重点)
2.能用平行直线的方向向量的位置关系解决实际问题(难点)
探究新知
思考:怎样确定空间中一个点的位置
空间中要确定一个点,必须是在个参照系中进行,这就是空间直角坐标系.这样可以通过点的位置向量进行确定.
问题1:(1)如图所示的四面体中,怎样借助空间向量来描述在空间中是不同的点
一、空间中的点与空间向量
可以借助向量的不同,描述在空间中是不同的点
探究新知
一般地,如果在空间中指定一点,那么空间中任意一点的位置,都可以由向量唯一确定,此时,通常称为点的位置向量.
特别地,空间直角坐标系中的任意一点都由它的位置向量唯一确定,从而也就由它的坐标唯一确定.
(2) 怎样借助空间向量来刻画空间中点的位置
探究新知
问题2:(1)如图所示的长方体中,设,如果只借助,能不能确定直线在空间中的位置
(2)一般地,怎样借助空间向量来刻画空间中直线的位置
结论:一般地,如果是空间中的一条直线,是空间中的一个非零向量,且表示的有向线段所在的直线与平行或重合,则称为直线的一个方向向量.此时,也称向量与直线平行,记作
二、空间中的直线与空间向量
探究新知
(1)如果,是直线上两个不同的点,则就是直线的一个方向向量
(2)如果是直线的一个方向向量,则对任意的实数,空间向量也是直线的一个方向向量,而且直线的任意两个方向向量都平行.
(3)如果是直线的一个方向向量,是直线的一个方向向量,则,或与重合.
注意:
(3)可用来判断两条直线是否平行.
向量可以描述所有与直线平行或重合的直线
只借助向量能否确定直线在空间中的位置
如图,因为,所以只借助向量不能确定直线在空间中的位置.
那要怎样确定直线在空间中的位置呢 需要增加什么条件呢
如果为直线的一个方向向量,为直线上一个已知的点,则对于直线上任意一点,向量一定与非零向量平行,从而可知存在唯一的实数,使得,这就是说,空间中直线的位置可由和点唯一确定.
探究新知
空间直线的向量参数方程
1.给定一个定点和一个向量,再任给一个实数,以为起点作向量.①
如图所示当变化时,点的轨迹形成直线,向量方程①称为直线以为参数的参数方程,向量称为该直线的方向向量,如图所示
探究新知
2.对空间任一个确定的点(如图所示),点在直线上的充要条件是存在唯一的实数,满足等式 ②
探究新知
如果在上取,则②式可化为,即.③
①或②或③三个向量等式都叫空间直线的向量参数方程
探究新知
注意:
直线的向量参数方程③有时也可表示为
.④
方程③和④可以用于判定三点共线.
即若或,
则三点共线,反之亦成立.
探究新知
点在平面内的充要条件
1.由共面向量定理,我们还可得到:
如果三点不共线,则点在平面内的充要条件是存在一对实数,使向量表达式成立
2.对于空间任意一点,有,这也是点在平面内的充要条件.
典例讲解
例1.已知正方体中,为的中点,
求证:直线与直线不平行.
证明:
以为原点,的方向分别为轴、轴、轴正方向,正方体的棱长为单位长度,建立如图所示的空间直角坐标系,则
所以,
又因为,所以与不平行.
因为为直线的一个方向向量, 为直线的一个方向向量,当∥ 时,必有∥ .
由上可知直线与直线不平行.
典例讲解
例2.(1)若在直线上,则直线的一个方向向量为( )
典例讲解
(2)直线的方向向量为,平面内两共点向量,下列关系中能表示的是( )
D.以上均不能
解析:
(1) ,而与共线的非零向量都可以作为直线的方向向量.答案: A
(2) 显然不能,而能表示或.答案:D
变式训练
1.已知点,为线段上一点且,则点的坐标为( )
解析:
设,∵为线段上一点且
∴,即
答案:C
2.已知正方体,点,分别是面对角线与面对角线的中点.求证:∥侧面, ∥,并且.
变式训练
解析:
如图,设,则,因此.
因为不在平面内,所以∥平面.
又因为,所以,
因此
对直线的方向向量的理解:
(1)非零性:直线的方向向量是非零向量
(2)不唯一性:直线的方向向量有无数个,可以分为方向相同和相反两类,它们都是共线向量
(3)给定空间中的任一点和非零向量,就可以确定唯一一条过点且平行于向量的直线
素养提炼
素养提炼
注意区分直线平行与向量平行的不同:
两直线平行时,其方向向量一定平行;但两直线的方向向量平行时,两直线平行或重合,切勿混淆直线与直线平行和向量与向量平行的含义
当堂练习
1.已知线段的两端点的坐标为,则线段与哪个坐标平面平行( )
或
解析:由题可知.答案:C
2.从点沿向量的方向取线段长,则点的坐标为( )
解析:设,由题可知,从而,由此列出方程,将各选项代入求解.答案:
当堂练习
3.已知分别是直线的方向向量,若,则( )
解析:由题可知,从而
答案:D
当堂练习
4.已知,点,在平面内,则_________.
解析:∴点在平面内,∴存在实数,使,即,∴
解得,
即.答案:11
归纳小结
空间中的点、直线与空间向量
用空间向量表示空间中的点
用空间向量表示直线
用向量证明平行关系
作 业
教材P36页练习A第1,2,4,5题
练习B第2题
