人教B版(2019)高中数学选择性必修第一册 《1.2空间中的平面与空间向量》名师课件(共32张PPT)
文档属性
| 名称 | 人教B版(2019)高中数学选择性必修第一册 《1.2空间中的平面与空间向量》名师课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-04 00:00:00 | ||
图片预览










文档简介
(共32张PPT)
复习引入
一、空间中两条直线所成的角
或
二、异面直线与空间向量
“不共面”是“与异面”的充要条件
复习引入
公垂线存在并且唯一
一般地,如果与是空间中两条异面直线,
,则称为与的公垂线段.
两条异面直线的公垂线段的长称为这两条异面直线之间的距离
人教B版同步教材名师课件
空间中的平面与空间向量
学习目标
学 习 目 标 核心素养
理解平面的法向量的概念 数学抽象
掌握线面垂直的判定定理以及三垂线定理及其逆定理 逻辑推理
会用向量方法证明两平面的平行和垂直 数学运算
1.理解平面的法向量的概念,会求平面的法向量.(重点)
2.会用平面的法向量证明平行与垂直.(重点)
3.理解并会应用三垂线定理及其逆定理证明有关垂直问题.(难点)
学习目标
探究新知
我们已经知道,空间中的直线,根据它的方向向量和一个点,可以描述这条直线的位置.那么,对于空间中的平面,能否引进类似的向量来描述其位置
直线有方向向量,那么能推广到平面吗
一、平面的法向量
定义:如果是空间中的一个平面,是空间中的一个非零向量,且表示的有向线段所在的直线与平面垂直,则称为平面的一个法向量.
此时,也称与平面垂直,记作⊥.
探究新知
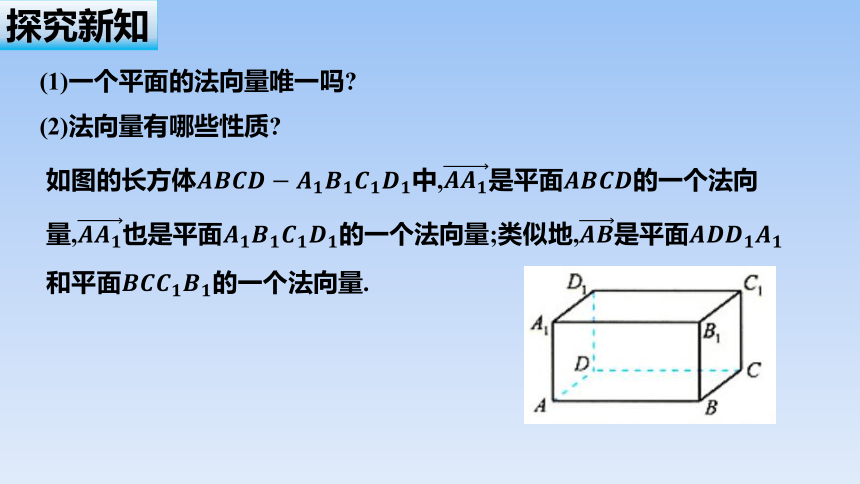
(1)一个平面的法向量唯一吗
(2)法向量有哪些性质
如图的长方体中,是平面的一个法向量,也是平面的一个法向量;类似地,是平面
和平面的一个法向量.
探究新知
①如果直线垂直平面,则直线的任意一个方向向量都是平面的一个法向量;
②如果是平面的一个法向量,则对任意的实数,空间向量也是平面的一个法向量,而且平面的任意两个法向量都平行;
③如果为平面的一个法向量,为平面上一个已知的点,则对于平面上任意一点,向量一定与向量垂直,即,从而可知平面的位置可由和唯一确定
(1)如果是直线的一个方向向量,是平面的一个法向量,分别探讨∥与⊥时,直线与平面的关系;
(2)如果是平面的一个法向量, 是平面的一个法向量,分别探讨⊥ 与∥时,平面与平面的关系,
探究新知
或
或与重合
典例讲解
例1.已知正方体中,,分别是与的中点求证:∥面
证明:以为原点,的方向分别为轴、轴、轴正方向,正方体的棱长为单位长度,建立如图所示的空间直角坐标系
则,又因为是的中点,所以的坐标为,
即,类似地,可得.因此.
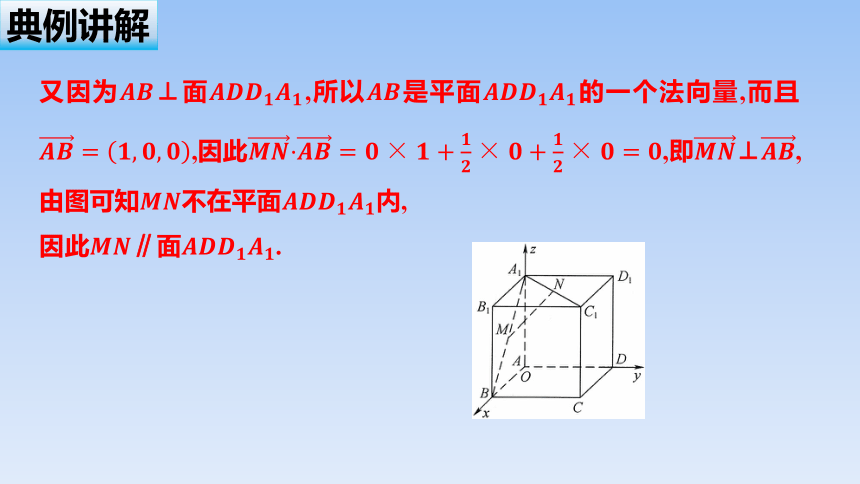
又因为⊥面,所以是平面的一个法向量,而且,因此,即⊥,由图可知不在平面内,
因此∥面.
典例讲解
例2.如图所示,已知空间直角坐标系中的三棱锥中,
,其中,求平面的一个法向量.
典例讲解
解析:由已知可得
设平面的一个法向量为,则
将看成常数,可解得
令,则
因此为平面的一个法向量.
法向量的求解:
如果是平面内不共线的三点,非零空间向量满足⊥,⊥,则是平面的一个法向量根据这一结论,通过设未知数解方程组,即可求得平面的一个法向量.
典例讲解
变式训练
1.在正方体中,求证:是平面的法向量.
解析:设正方体棱长为1,以为单位正交基底,建立如图所示的空间直角坐标系,则,
,
所以同理,.又因为
所以⊥平面,从而是平面的法向量
变式训练
2.已知平面上的两个向量,则平面的一个法向量为( )
解析:显然与不平行,设平面的一个法向量为
则,所以,令,得,
所以
答案:C
3.直线的一个方向向量和平面的一个法向量分别是
,则直线与平面的位置关系是( )
. . 或 .无法判断
变式训练
解析:,所以⊥,所以或
答案:
探究新知
二、三垂线定理及其逆定理
射影:已知空间中的平面以及点,过作的垂线,设与相交于点,则就是点在平面内的射影(也称为投影).
空间中,图形上所有点在平面内的射影所组成的集合,称为图形在平面内的射影.
如图所示,如果的顶点在平面内,与都在平面外,则分别过与作的垂线,设交点分别为,则
就是在平面内的射影.而且,此时与都是平面的一个法向量
探究新知
探究新知
已知是平面的一条斜线且为斜足(即不垂直于,且),设其中是A在平面内的射影,而是平面内的一条直线,如图所示.判断下列命题是否成立,并用空间向量证明:
(1)当⊥时,⊥;(2)当⊥时,⊥.
设∥,则由且可知,即.
如果,则,又因为,所以,因此.
如果,则,又因为,所以,因此
这两个结论一般称为三垂线定理及其逆定理
探究新知
三垂线定理:如果平面内的一条直线与平面的一条斜线在该平面内的射影垂直,则它也和这条斜线垂直
三垂线定理的逆定理:如果平面内的一条直线和这个平面的一条斜线垂直,则它也和这条斜线在该平面内的射影垂直
探究新知
符号语言:
(1)当⊥时,⊥;(2)当⊥时,⊥.
典例讲解
例3.如图所示,已知是一个正方体,求证:
证明:
连接因为是正方体,所以⊥面,因此在平面内的射影为
又因为是正方形,所以⊥,因此根据三垂线定理可知⊥
典例讲解
例4.如图所示的三棱锥中,,且为的边上的高,求证:⊥
证明:
因为⊥,⊥,,所以⊥面.因此在平面内的射影为,又因为⊥,所以根据三垂线定理的逆定理可知⊥.
变式训练
4.在正方体中,分别是棱,,的中点,求证:⊥平面
解析:如图,连接AC,BD,∵,分别是,的中点,∴∥,又⊥,∴⊥.又∵⊥底面,∴依据三垂线定理,有⊥.
设的中点为,则⊥侧面.
设与相交于点,易证.
∴,
∴根据三垂线定理,得
又,∴⊥平面
变式训练
5.在空间四边形中,⊥平面,⊥,若在,上的射影分别为,.求证:⊥.
解析:如图,因为⊥平面,所以⊥又因为⊥,∩=,所以⊥平面.而平面,所以⊥.
又因为是点在上的射影,所以⊥.
又,所以⊥平面.
所以在平面内的射影为.
又因为为在上的射影,所以⊥.
由三垂线定理的逆定理知⊥.
素养提炼
用代数法求平面的一个法向量的步骤为
(1)设平面的一个法向量;
(2)在已知平面内找两个不共线的向量
(3)建立方程组
(4)解方程组:先用一个未知量表示其他两个未知量,然后对用来表示两未知量的未知量赋以特殊值,从而得到平面的一个法向量.
关于三垂线定理的理解
(1)三垂线定理叙述的是平面内直线与平面的斜线,及斜线在平面内的投影三者之间的垂直关系
(2)这里与可以相交,可以异面
(3)三垂线定理是判断或证明空间中线线垂直的主要依据,三垂线定理跨越了线面垂直,直接由线线垂直到线线垂直,为解决线线垂直提供了一条捷径.
素养提炼
注意:方程组,有无数多组解,只需给中一个变量赋一个特殊值,即可确定平面的一个法向量,注意.
当堂练习
1.若是平面的一个法向量,则下列向量中能作为平面的另一个法向量的是( )
解析:一个平面的法向量不唯一,但这些法向量间是共线的,即存在非零倍数的关系.答案:
2.若不重合的平面与的法向量分别是,则平面与平面的关系是( )
A.平行 B.垂直 C.相交但不垂直 D.无法判断
解析:因为,所以,所以.答案:A
3.平面,的法向量分别为,若⊥,则等于__________.
解析:由知,所以,
解得.答案:
当堂练习
4.已知,则平面的单位法向量坐标为__________.
解析:设所求单位法向量为由题意.由且得,所以答案:或
当堂练习
5.如图,是的斜边,过点作所在平面的垂线,连接,,过点作⊥于点,连接,则图中的直角三角形的个数为__________.
解析:∵⊥平面,∴在平面内的射影为
∵⊥,由三垂线定理可得⊥,
均为直角三角形,共8个答案:8
归纳小结
平面的法向量
平面的法向量
平面法向量的概念
平面法向量的性质
平面法向量的应用
线面、面面平行的判定
线面、面面垂直的判定
三垂线定理
三垂线定理的逆定理
射影的概念
三垂线定理
作 业
教材P41页练习A第1,2,3题
练习B第3,4,5题
复习引入
一、空间中两条直线所成的角
或
二、异面直线与空间向量
“不共面”是“与异面”的充要条件
复习引入
公垂线存在并且唯一
一般地,如果与是空间中两条异面直线,
,则称为与的公垂线段.
两条异面直线的公垂线段的长称为这两条异面直线之间的距离
人教B版同步教材名师课件
空间中的平面与空间向量
学习目标
学 习 目 标 核心素养
理解平面的法向量的概念 数学抽象
掌握线面垂直的判定定理以及三垂线定理及其逆定理 逻辑推理
会用向量方法证明两平面的平行和垂直 数学运算
1.理解平面的法向量的概念,会求平面的法向量.(重点)
2.会用平面的法向量证明平行与垂直.(重点)
3.理解并会应用三垂线定理及其逆定理证明有关垂直问题.(难点)
学习目标
探究新知
我们已经知道,空间中的直线,根据它的方向向量和一个点,可以描述这条直线的位置.那么,对于空间中的平面,能否引进类似的向量来描述其位置
直线有方向向量,那么能推广到平面吗
一、平面的法向量
定义:如果是空间中的一个平面,是空间中的一个非零向量,且表示的有向线段所在的直线与平面垂直,则称为平面的一个法向量.
此时,也称与平面垂直,记作⊥.
探究新知
(1)一个平面的法向量唯一吗
(2)法向量有哪些性质
如图的长方体中,是平面的一个法向量,也是平面的一个法向量;类似地,是平面
和平面的一个法向量.
探究新知
①如果直线垂直平面,则直线的任意一个方向向量都是平面的一个法向量;
②如果是平面的一个法向量,则对任意的实数,空间向量也是平面的一个法向量,而且平面的任意两个法向量都平行;
③如果为平面的一个法向量,为平面上一个已知的点,则对于平面上任意一点,向量一定与向量垂直,即,从而可知平面的位置可由和唯一确定
(1)如果是直线的一个方向向量,是平面的一个法向量,分别探讨∥与⊥时,直线与平面的关系;
(2)如果是平面的一个法向量, 是平面的一个法向量,分别探讨⊥ 与∥时,平面与平面的关系,
探究新知
或
或与重合
典例讲解
例1.已知正方体中,,分别是与的中点求证:∥面
证明:以为原点,的方向分别为轴、轴、轴正方向,正方体的棱长为单位长度,建立如图所示的空间直角坐标系
则,又因为是的中点,所以的坐标为,
即,类似地,可得.因此.
又因为⊥面,所以是平面的一个法向量,而且,因此,即⊥,由图可知不在平面内,
因此∥面.
典例讲解
例2.如图所示,已知空间直角坐标系中的三棱锥中,
,其中,求平面的一个法向量.
典例讲解
解析:由已知可得
设平面的一个法向量为,则
将看成常数,可解得
令,则
因此为平面的一个法向量.
法向量的求解:
如果是平面内不共线的三点,非零空间向量满足⊥,⊥,则是平面的一个法向量根据这一结论,通过设未知数解方程组,即可求得平面的一个法向量.
典例讲解
变式训练
1.在正方体中,求证:是平面的法向量.
解析:设正方体棱长为1,以为单位正交基底,建立如图所示的空间直角坐标系,则,
,
所以同理,.又因为
所以⊥平面,从而是平面的法向量
变式训练
2.已知平面上的两个向量,则平面的一个法向量为( )
解析:显然与不平行,设平面的一个法向量为
则,所以,令,得,
所以
答案:C
3.直线的一个方向向量和平面的一个法向量分别是
,则直线与平面的位置关系是( )
. . 或 .无法判断
变式训练
解析:,所以⊥,所以或
答案:
探究新知
二、三垂线定理及其逆定理
射影:已知空间中的平面以及点,过作的垂线,设与相交于点,则就是点在平面内的射影(也称为投影).
空间中,图形上所有点在平面内的射影所组成的集合,称为图形在平面内的射影.
如图所示,如果的顶点在平面内,与都在平面外,则分别过与作的垂线,设交点分别为,则
就是在平面内的射影.而且,此时与都是平面的一个法向量
探究新知
探究新知
已知是平面的一条斜线且为斜足(即不垂直于,且),设其中是A在平面内的射影,而是平面内的一条直线,如图所示.判断下列命题是否成立,并用空间向量证明:
(1)当⊥时,⊥;(2)当⊥时,⊥.
设∥,则由且可知,即.
如果,则,又因为,所以,因此.
如果,则,又因为,所以,因此
这两个结论一般称为三垂线定理及其逆定理
探究新知
三垂线定理:如果平面内的一条直线与平面的一条斜线在该平面内的射影垂直,则它也和这条斜线垂直
三垂线定理的逆定理:如果平面内的一条直线和这个平面的一条斜线垂直,则它也和这条斜线在该平面内的射影垂直
探究新知
符号语言:
(1)当⊥时,⊥;(2)当⊥时,⊥.
典例讲解
例3.如图所示,已知是一个正方体,求证:
证明:
连接因为是正方体,所以⊥面,因此在平面内的射影为
又因为是正方形,所以⊥,因此根据三垂线定理可知⊥
典例讲解
例4.如图所示的三棱锥中,,且为的边上的高,求证:⊥
证明:
因为⊥,⊥,,所以⊥面.因此在平面内的射影为,又因为⊥,所以根据三垂线定理的逆定理可知⊥.
变式训练
4.在正方体中,分别是棱,,的中点,求证:⊥平面
解析:如图,连接AC,BD,∵,分别是,的中点,∴∥,又⊥,∴⊥.又∵⊥底面,∴依据三垂线定理,有⊥.
设的中点为,则⊥侧面.
设与相交于点,易证.
∴,
∴根据三垂线定理,得
又,∴⊥平面
变式训练
5.在空间四边形中,⊥平面,⊥,若在,上的射影分别为,.求证:⊥.
解析:如图,因为⊥平面,所以⊥又因为⊥,∩=,所以⊥平面.而平面,所以⊥.
又因为是点在上的射影,所以⊥.
又,所以⊥平面.
所以在平面内的射影为.
又因为为在上的射影,所以⊥.
由三垂线定理的逆定理知⊥.
素养提炼
用代数法求平面的一个法向量的步骤为
(1)设平面的一个法向量;
(2)在已知平面内找两个不共线的向量
(3)建立方程组
(4)解方程组:先用一个未知量表示其他两个未知量,然后对用来表示两未知量的未知量赋以特殊值,从而得到平面的一个法向量.
关于三垂线定理的理解
(1)三垂线定理叙述的是平面内直线与平面的斜线,及斜线在平面内的投影三者之间的垂直关系
(2)这里与可以相交,可以异面
(3)三垂线定理是判断或证明空间中线线垂直的主要依据,三垂线定理跨越了线面垂直,直接由线线垂直到线线垂直,为解决线线垂直提供了一条捷径.
素养提炼
注意:方程组,有无数多组解,只需给中一个变量赋一个特殊值,即可确定平面的一个法向量,注意.
当堂练习
1.若是平面的一个法向量,则下列向量中能作为平面的另一个法向量的是( )
解析:一个平面的法向量不唯一,但这些法向量间是共线的,即存在非零倍数的关系.答案:
2.若不重合的平面与的法向量分别是,则平面与平面的关系是( )
A.平行 B.垂直 C.相交但不垂直 D.无法判断
解析:因为,所以,所以.答案:A
3.平面,的法向量分别为,若⊥,则等于__________.
解析:由知,所以,
解得.答案:
当堂练习
4.已知,则平面的单位法向量坐标为__________.
解析:设所求单位法向量为由题意.由且得,所以答案:或
当堂练习
5.如图,是的斜边,过点作所在平面的垂线,连接,,过点作⊥于点,连接,则图中的直角三角形的个数为__________.
解析:∵⊥平面,∴在平面内的射影为
∵⊥,由三垂线定理可得⊥,
均为直角三角形,共8个答案:8
归纳小结
平面的法向量
平面的法向量
平面法向量的概念
平面法向量的性质
平面法向量的应用
线面、面面平行的判定
线面、面面垂直的判定
三垂线定理
三垂线定理的逆定理
射影的概念
三垂线定理
作 业
教材P41页练习A第1,2,3题
练习B第3,4,5题
