第6单元多边形的面积练习卷小学数学五年级上册人教版(含答案)
文档属性
| 名称 | 第6单元多边形的面积练习卷小学数学五年级上册人教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-05 18:50:23 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第6单元多边形的面积练习卷-小学数学五年级上册人教版
一、选择题
1.一块近似三角形的菜地,它的面积大约是160平方米,高约是4米,底约是( )。
A.20米 B.40米 C.80米 D.120米
2.两个完全一样的三角形一定可以拼成一个( )。
A.平行四边形 B.长方形 C.正方形 D.梯形
3.如图所示,( )面积大。
A.甲 B.乙 C.相等 D.无法确定
4.边长为8厘米的正方形一组对边上各有一条长1厘米的线段,图中阴影部分的面积是( )平方厘米。
A.1 B.4 C.8
5.计算下图平行四边形面积的正确算式是( )。
A.12×10 B.7.5×12 C.9×12 D.7.5×10
6.有一个可活动的平行四边形框架,把它拉成长方形,下面说法正确的是( )。
A.周长不变,面积不变 B.周长不变,面积变小
C.周长不变,面积变大 D.周长变大,面积不变
7.在面积为42平方米的平行四边形内画一个最大的三角形,这个三角形的面积是( )平方米。
A.30 B.21 C.14 D.20
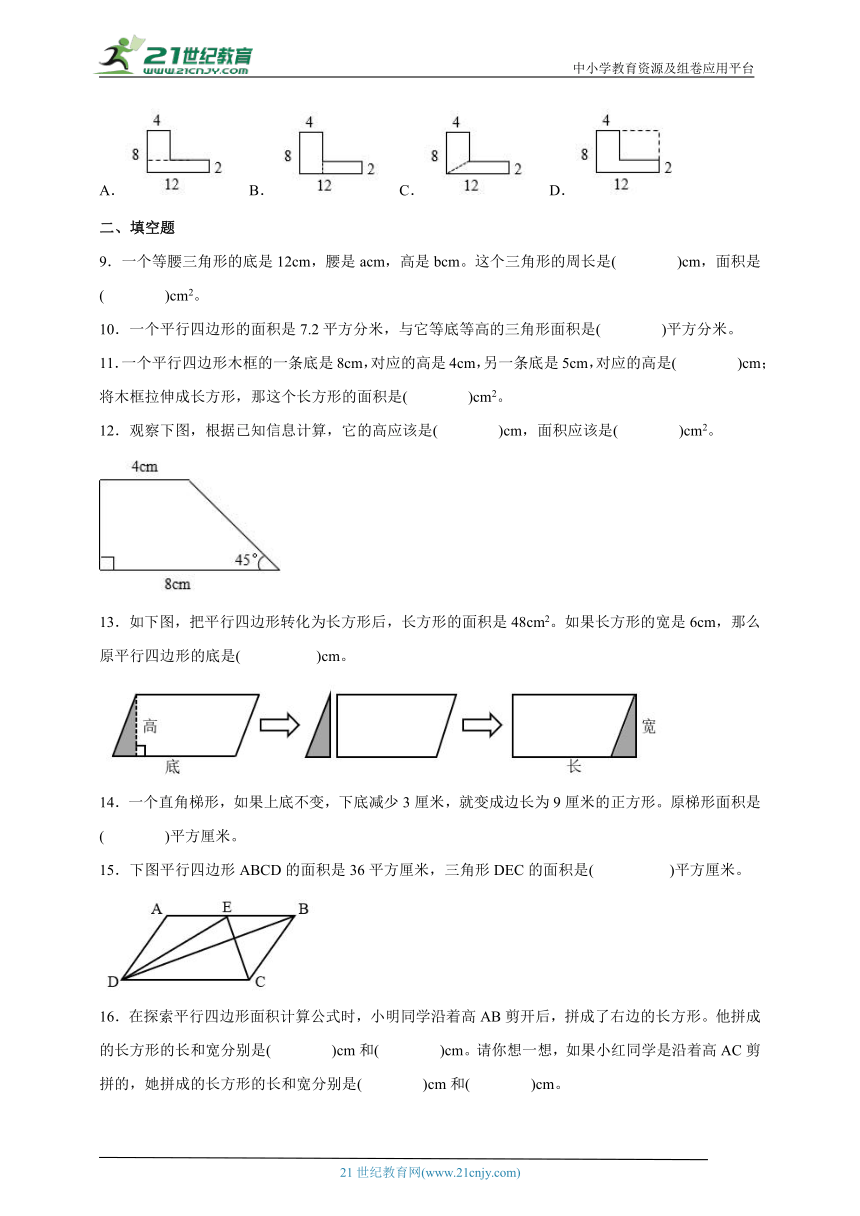
8.下面组合图形的面积,用算式“(8-2)×4+12×2”求的是( )。
A. B. C. D.
二、填空题
9.一个等腰三角形的底是12cm,腰是acm,高是bcm。这个三角形的周长是( )cm,面积是( )cm2。
10.一个平行四边形的面积是7.2平方分米,与它等底等高的三角形面积是( )平方分米。
11.一个平行四边形木框的一条底是8cm,对应的高是4cm,另一条底是5cm,对应的高是( )cm;将木框拉伸成长方形,那这个长方形的面积是( )cm2。
12.观察下图,根据已知信息计算,它的高应该是( )cm,面积应该是( )cm2。
13.如下图,把平行四边形转化为长方形后,长方形的面积是48cm2。如果长方形的宽是6cm,那么原平行四边形的底是( )cm。
14.一个直角梯形,如果上底不变,下底减少3厘米,就变成边长为9厘米的正方形。原梯形面积是( )平方厘米。
15.下图平行四边形ABCD的面积是36平方厘米,三角形DEC的面积是( )平方厘米。
16.在探索平行四边形面积计算公式时,小明同学沿着高AB剪开后,拼成了右边的长方形。他拼成的长方形的长和宽分别是( )cm和( )cm。请你想一想,如果小红同学是沿着高AC剪拼的,她拼成的长方形的长和宽分别是( )cm和( )cm。
三、判断题
17.周长相等的长方形和平行四边形的面积一定相等。( )
18.平行四边形的底增加2厘米,高减少2厘米后面积不变。( )
19.两个面积相等的直角梯形一定等底等高。( )
20.每个小方格是1cm2,洋洋估测“树叶”的面积是12cm2。( )
21.在一个长方形纸上剪下一个最大的三角形,三角形的面积是长方形面面积的一半。( )
四、图形计算
22.求如图图形的面积。(单位:厘米)
23.计算下列图形阴影部分的面积。(单位:cm)
五、解答题
24.有一块三角形的麦田,底275米,高60米,共收小麦19.8吨。这块麦田有多少公顷?平均每公顷收小麦多少吨?
25.某小区在靠墙边的一块空地上新建了一个近似梯形的花坛,围成花坛的篱笆全长是56米,其中近似高的一段长是20米(如图)。这个花坛的面积大约是多少?
26.爱民小学有一块校内劳动基地(如图)。学校把它分成一个平行四边形和一个三角形,平行四边形地里种大白菜,三角形地里种萝卜。
(1)每棵大白菜占地0.15平方米,一共可以种多少棵?
(2)萝卜地有多少平方米?
27.王伯伯有一块近似平行四边形的菜地,为了方便浇灌,中间留了一条小路。如果每平方米青菜能卖50元钱,这块地的青菜一共可以卖多少元?
28.一个梯形果园,上底长18米,比下底短5米,高16米。现在在这个果园里栽上梨树,每棵梨树占地4平方米。
(1)这个果园的面积多少平方米?
(2)这个果园可以栽多少棵梨树?
参考答案:
1.C
【分析】根据三角形的面积公式:S=ab÷2,由此可知a=2S÷b,用160乘2,再除以4计算即可。
【详解】160×2÷4
=320÷4
=80(米)
则它的底是80米。
故答案为:C
【点睛】本题考查三角形的面积,灵活运用三角形的面积公式是解题的关键。
2.A
【分析】长方形和正方形是特殊的平行四边形,两个完全一样的直角三角形可以拼成长方形,两个完全一样的等腰直角三角形可以拼成正方形。如图 ,两个完全一样的三角形一定可以拼成一个平行四边形。
【详解】A.两个完全一样的三角形一定可以拼成一个平行四边形;
B.如图 完全一样的三角形不能拼成长方形;
C.如图完全一样的三角形不能拼成正方形;
D.两个完全一样的三角形不能拼成梯形。
故答案为:A
【点睛】关键是熟悉平面图形的特征,拆拼图形时,考虑图形剪开后各部分的形状、大小、位置的关系。
3.A
【分析】根据图,甲、乙都是三角形,三角形的面积=底×高÷2。那么,选定合适的底和高,分析出甲、乙的面积关系即可。
【详解】以梯形的上底为甲的底,梯形的下底为乙的底,此时两个三角形的高相等。又因为,这个梯形的上底大于下底,所以甲的底大于乙的底,所以甲的面积大一些。
故答案为:A
【点睛】本题考查了三角形的面积,熟记面积公式是解题的关键。
4.B
【分析】先根据“三角形的面积=底×高÷2”分别求出两个三角形的面积,再求出两个三角形的面积和。
【详解】如下图,设上面的三角形1厘米的底边所对应的高为,下面的三角形1厘米的底边所对应的高是厘米,则有+=8厘米。
上面的三角形的面积:1×÷2=÷2
下面的三角形的面积:1×÷2=÷2
两个三角形的面积和:÷2+÷2
=(+)÷2
=8÷2
=4(平方厘米)
故答案为:B
【点睛】明确两个三角形高的和与正方形边长的关系是解决此题的关键。
5.B
【分析】观察平行四边形可知,12cm的底对应的高是7.5cm,9cm的底对应的高是10cm,根据平行四边形的面积公式,可用12×7.5或9×10即可求出平行四边形的面积。
【详解】12×7.5=90(cm2)
9×10=90(cm2)
计算平行四边形面积的正确算式是12×7.5或9×10。
故答案为:B
【点睛】本题考查了平行四边形的面积公式的灵活应用,关键是找到底边对应的高。
6.C
【分析】把一个活动的平行四边形框架拉成一个长方形,四个边的长度没变,则其周长不变;根据长方形的面积=长×宽,平行四边形的面积=底×高, 长方形的长和原来平行四边形的底相等,长方形的宽大于原来平行四边形的高,所以长方形的面积比原来平行四边形的面积变大了。
【详解】如图:
把一个活动的平行四边形框架拉成一个长方形,周长不变;由于拉成的长方形的宽大于原来平行四边形的高,所以面积变大了。
故答案为:C
【点睛】掌握平行四边形拉成长方形后,长方形的长、宽分别与平行四边形的底和高之间的关系是解题的关键。
7.B
【分析】根据题意,在平行四边形内画一个最大的三角形,那么这个三角形与平行四边形等底等高;根据三角形的面积=底×高÷2,平行四边形的面积=底×高可知,等底等高的三角形的面积是平行四边形面积的一半,据此解答。
【详解】42÷2=21(平方米)
在面积为42平方米的平行四边形内画一个最大的三角形,这个三角形的面积是21平方米。
故答案为:B
【点睛】关键是明白在平行四边形内画一个最大的三角形,那么这个三角形与平行四边形等底等高,再利用等底等高的三角形的面积与平行四边形面积的关系解决问题。
8.A
【分析】根据选项中各图形的分割方法分别计算各组合图形的面积,最后找出和题目计算方法相同的选项,据此解答。
【详解】A.整个图形的面积=上面长方形的面积+下面长方形的面积。
(8-2)×4+12×2
=6×4+12×2
=24+24
=48
所以,组合图形的面积是48。
B.整个图形的面积=左边长方形的面积+右边长方形的面积。
8×4+(12-4)×2
=8×4+8×2
=32+16
=48
所以,组合图形的面积是48。
C.整个图形的面积=左边梯形的面积+右边梯形的面积。
(8-2+8)×4÷2+(12-4+12)×2÷2
=14×4÷2+20×2÷2
=28+20
=48
所以,组合图形的面积是48。
D.组合图形的面积=大长方形的面积-小长方形的面积。
12×8-(12-4)×(8-2)
=12×8-8×6
=96-48
=48
所以,组合图形的面积是48。
故答案为:A
【点睛】同一个图形的面积可能有多种不同的计算方法,掌握组合图形面积的计算方法是解答题目的关键。
9. 12+2a 6b
【分析】等腰三角形的周长是三条边长之和,根据等腰三角形的特征:两条腰是相等的;根据三角形面积=底×高÷2,代入相应数值即可完成解答。
【详解】12+a+a=12+2a(cm)
12×b÷2=6b(cm2)
所以这个等腰三角形的周长是(12+2a)cm,面积是(6b)cm2。
【点睛】解答本题的关键是掌握等腰三角形的面积及特征。
10.3.6
【分析】平行四边形的面积公式:平行四边形的面积=底×高,三角形的面积公式:三角形的面积=底×高÷2,已知三角形和平行四边形等底等高,这时三角形的面积是平行四边形面积的一半。据此解答。
【详解】7.2÷2=3.6(平方分米)
与平行四边形等底等高的三角形面积是3.6平方分米。
【点睛】本题考查了平行四边形和三角形面积之间的关系,需要明确平行四边形的面积是与它等底等高的三角形面积的2倍。
11. 6.4 40
【分析】(1)根据平行四边形的面积=底×高,先用8×4=32(cm2)求出平行四边形的面积,再用面积除以另一条底求出另一条底对应的高;
(2)将木框拉伸成长方形,那么平行四边形的一条底是长方形的长,另一条底是长方形的宽,根据长方形的面积=长×宽把数据代入求出长方形的面积。
【详解】8×4÷5
=32÷5
=6.4(cm)
8×5=40(cm2)
所以一个平行四边形木框的一条底是8cm,对应的高是4cm,另一条底是5cm,对应的高是6.4cm;将木框拉伸成长方形,那这个长方形的面积是40cm2。
【点睛】本题重点考查平行四边形和长方形的面积公式,明确拉伸过程中平行四边形和长方形的关系是解题的关键。
12. 4 24
【分析】如图:作出该梯形的另一条高,以这条高为界,右边是一个等腰直角三角形,所以该梯形的高是(8-4)cm;再根据梯形的面积公式:S=(a+b)h÷2,据此代入数值进行计算即可。
【详解】8-4=4(cm)
(4+8)×4÷2
=12×4÷2
=48÷2
=24(cm2)
则它的高应该是4cm,面积应该是24cm2。
【点睛】本题考查梯形的面积,熟记公式是解题的关键。
13.8
【分析】根据平行四边形面积公式的推导过程可知,把一个平行四边形割补成一个长方形,只是形状变了,面积不变,长方形的宽相当于平行四边形的高,长方形的长相当于平行四边形的底,已知长方形的面积是48cm2,长方形的宽是6cm,根据平行四边形的面积公式和长方形的面积公式,用48÷6即可求出原来平行四边形的底,据此解答。
【详解】48÷6=8(cm)
原平行四边形的底是8cm。
【点睛】本题主要考查平行四边形面积的推导过程,明确平行四边形无论割补成什么形状,面积没有发生变化。
14.94.5
【分析】一个直角梯形的上底不变,如果把下底减少3厘米,这个梯形就变成了正方形,可知这个梯形的上底是9厘米,下底是9+3=12厘米,高是9厘米,然后再根据梯形的面积公式进行计算。
【详解】9+3=12(厘米)
(9+12)×9÷2
=21×9÷2
=94.5(平方厘米)
即原梯形面积是94.5平方厘米。
【点睛】本题的主要考查了学生根据梯形的面积公式解答问题的能力,解答此题关键是求出下底的长,再根据公式求解。
15.18
【分析】因为三角形的面积S=ah÷2,平行四边形的面积S=ah,所以三角形的面积是与其等底等高的平行四边形的面积的一半;据此解答即可。
【详解】36÷2=18(平方厘米)
即三角形DEC的面积是18平方厘米。
【点睛】此题主要考查等底等高的三角形和平行四边形的面积的关系。
16. 2.4 2 3 1.6
【分析】根据平行四边形面积公式的推导过程可知,把一个平行四边形沿高AB剪开得到两部分,并把三角形部分向右平移与另一部分拼成一个长方形,拼成的长方形的长等于平行四边形的高,长方形的宽等于平行四边形的底。若沿高AC剪开得到的两部分,拼成的长方形的长等于平行四边形的底,长方形的宽等于平行四边形的高,据此解答。
【详解】在探索平行四边形面积计算公式时,小明同学沿着高AB剪开后,他拼成的长方形的长是2.4cm,宽是2cm。如果小红同学是沿着高AC剪拼的,她拼成的长方形的长是3cm,宽是1.6cm。
【点睛】解答本题的关键是理解掌握平行四边形面积公式的推导过程及应用。
17.×
【分析】长方形的面积=长×宽,平行四边形的面积=底×高,可假设长方形的长=平行四边形的底,长方形的宽=平行四边形的一条斜边,那么长方形的宽>平行四边形的高,所以长×宽>底×高,则长方形的面积>平行四边形的面积,故面积-定不相等。
【详解】由分析可知:周长相等的长方形和平行四边形的面积一定相等,说法错误。
故答案为:×
【点睛】本题考查了学生对平行四边形、长方形面积公式的理解和运用。
18.×
【分析】假设出原来平行四边形的底和高,平行四边形的面积=底×高,求出原来平行四边形的面积和现在平行四边形的面积,即可求得。
【详解】假设原来平行四边形的底为3厘米,高为4厘米。
原来平行四边形的面积:3×4=12(平方厘米)
现在平行四边形的面积:(3+2)×(4-2)
=5×2
=10(平方厘米)
因为12平方厘米≠10平方厘米,所以平行四边形的面积变了。
故答案为:×
【点睛】掌握平行四边形的面积计算公式是解答题目的关键。
19.×
【分析】通过梯形的面积公式,举例论证此说法是错误的。
【详解】梯形①面积是20,则上底2,下底8,高是4。
梯形②的面积也是20,则上底是1.5,下底3.5,高是8。
它们的面积相等,但是底和高不相等。
故答案为:×
【点睛】此题的解题关键是利用梯形面积公式,用举例的方式,进行论证,证明题干的说法是错误的。
20.√
【分析】首先把图形用方格划分,注意每一部分估算取整,其中不足1格的按照半格计算,最后合并即可得出答案。
【详解】有7个整格子,大约10个半方格,大约7+10÷2=12个方格,因为每个小方格的面积是1cm2,因此面积为12cm2。
故答案为:√
【点睛】解决此题的关键是利用割补法,把不规则的图形拼为规则的图形,进一步估算面积即可。
21.√
【分析】在长方形中剪出的最大三角形,它的底和长方形的长相等,高和长方形的宽相等。据此结合长方形和三角形的面积公式,推断和这个三角形和长方形的面积关系即可。
【详解】在一个长方形纸上剪下一个最大的三角形,三角形面积=长×宽÷2,长方形面积=长×宽,所以这个三角形的面积是长方形面面积的一半。
所以判断正确。
【点睛】本题考查了三角形和长方形的面积,熟记面积公式是解题的关键。
22.546平方厘米;615平方厘米
【分析】(1)梯形的上底为13厘米,下底为26厘米,高为28厘米,利用“梯形的面积=(上底+下底)×高÷2”求出梯形的面积;
(2)整个图形的面积=上面三角形的面积+下面梯形的面积,据此解答。
【详解】(1)(13+26)×28÷2
=39×28÷2
=1092÷2
=546(平方厘米)
所以,该图形的面积是546平方厘米。
(2)35-20=15(厘米)
18×15÷2+(18+30)×20÷2
=18×15÷2+48×20÷2
=270÷2+960÷2
=135+480
=615(平方厘米)
所以,该图形的面积是615平方厘米。
23.64cm2;60cm2
【分析】观察图形可知,第一个阴影部分是一个上底为4cm,下底为(4×3)cm,高为8cm的梯形,根据梯形的面积公式求解即可;
第二个阴影部分的面积等于一个底为12cm,高为10cm的平行四边形面积减去一个底为12cm,高为10cm的三角形面积,根据平行四边形的面积公式和三角形的面积公式求解即可。
【详解】4×3=12(cm)
(12+4)×8÷2
=16×8÷2
=128÷2
=64(cm2)
第一个阴影部分的面积是64cm2。
12×10-12×10÷2
=120-60
=60(cm2)
第二个阴影部分的面积是60cm2。
24.0.825公顷;24吨
【分析】根据三角形的面积=底×高÷2,代入相应数值计算,所得结果即为这块麦田的面积;要求平均每公顷收小麦多少吨,用小麦的总吨数除以这块麦田的面积,据此解答。
【详解】275×60÷2
=16500÷2
=8250(平方米)
8250平方米=0.825公顷
19.8÷0.825=24(吨)
答:这块麦田的有0.825公顷,平均每公顷收小麦24吨。
【点睛】解答本题的关键是掌握三角形面积的计算公式,同时要弄清谁是单一量,再用另一个量进行平均分。
25.360平方米
【分析】通过篱笆全长是56米与近似高为20米,可以求出上底与下底的和,再通过梯形的面积公式(上底+下底)×高÷2,即可求解。
【详解】(56-20)×20÷2
=36×20÷2
=720÷2
=360(平方米)
答:这个花坛的面积大约是360平方米。
【点睛】此题考查梯形的面积,解题关键为求到上下底的和,熟练掌握梯形的面积公式,即可解题。
26.(1)400棵;
(2)22.5平方米
【分析】(1)利用“平行四边形的面积=底×高”求出白菜地的面积,一共可以种白菜的棵数=白菜地的面积÷每棵白菜的占地面积;
(2)三角形的底为(14-8)米,三角形的高和平行四边形的高相等,利用“三角形的面积=底×高÷2”求出萝卜地的面积,据此解答。
【详解】(1)8×7.5÷0.15
=60÷0.15
=400(棵)
答:一共可以种400棵。
(2)(14-8)×7.5÷2
=6×7.5÷2
=45÷2
=22.5(平方米)
答:萝卜地有22.5平方米。
【点睛】掌握平行四边形和三角形的面积计算公式是解答题目的关键。
27.10000元
【分析】菜地面面积=原来菜地面积-中间小路的面积,通过图形的平移,菜地的面积可以看作是底为(21-1)米,高为10米的平行四边形面积,平行四边形面积=底×高,青菜可卖出的总价=菜地面积×每平方米青菜可卖钱数,据此解答。
【详解】(21-1)×10
=20×10
=200(平方米)
200×50=10000(元)
答:这块地的青菜一共可以卖10000元。
【点睛】本题考查平行四边形的面积公式以及根据总价、数量和单价之间的关系来解决问题。
28.(1)328平方米;
(2)82棵
【分析】(1)下底=上底+5米,求出下底,再根据梯形的面积=(上底+下底)×高÷2,代入数据,即可求出果园的面积。
(2)用果园的面积除以每棵梨树占地的面积,即可求出这个果园可以栽多少棵梨树。
【详解】(1)18+5=23(米)
(18+23)×16÷2
=41×16÷2
=328(平方米)
答:这个果园的面积是328平方米。
(2)328÷4=82(棵)
答:这个果园可以栽82棵梨树。
【点睛】此题的解题关键是灵活运用梯形的面积公式求解。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第6单元多边形的面积练习卷-小学数学五年级上册人教版
一、选择题
1.一块近似三角形的菜地,它的面积大约是160平方米,高约是4米,底约是( )。
A.20米 B.40米 C.80米 D.120米
2.两个完全一样的三角形一定可以拼成一个( )。
A.平行四边形 B.长方形 C.正方形 D.梯形
3.如图所示,( )面积大。
A.甲 B.乙 C.相等 D.无法确定
4.边长为8厘米的正方形一组对边上各有一条长1厘米的线段,图中阴影部分的面积是( )平方厘米。
A.1 B.4 C.8
5.计算下图平行四边形面积的正确算式是( )。
A.12×10 B.7.5×12 C.9×12 D.7.5×10
6.有一个可活动的平行四边形框架,把它拉成长方形,下面说法正确的是( )。
A.周长不变,面积不变 B.周长不变,面积变小
C.周长不变,面积变大 D.周长变大,面积不变
7.在面积为42平方米的平行四边形内画一个最大的三角形,这个三角形的面积是( )平方米。
A.30 B.21 C.14 D.20
8.下面组合图形的面积,用算式“(8-2)×4+12×2”求的是( )。
A. B. C. D.
二、填空题
9.一个等腰三角形的底是12cm,腰是acm,高是bcm。这个三角形的周长是( )cm,面积是( )cm2。
10.一个平行四边形的面积是7.2平方分米,与它等底等高的三角形面积是( )平方分米。
11.一个平行四边形木框的一条底是8cm,对应的高是4cm,另一条底是5cm,对应的高是( )cm;将木框拉伸成长方形,那这个长方形的面积是( )cm2。
12.观察下图,根据已知信息计算,它的高应该是( )cm,面积应该是( )cm2。
13.如下图,把平行四边形转化为长方形后,长方形的面积是48cm2。如果长方形的宽是6cm,那么原平行四边形的底是( )cm。
14.一个直角梯形,如果上底不变,下底减少3厘米,就变成边长为9厘米的正方形。原梯形面积是( )平方厘米。
15.下图平行四边形ABCD的面积是36平方厘米,三角形DEC的面积是( )平方厘米。
16.在探索平行四边形面积计算公式时,小明同学沿着高AB剪开后,拼成了右边的长方形。他拼成的长方形的长和宽分别是( )cm和( )cm。请你想一想,如果小红同学是沿着高AC剪拼的,她拼成的长方形的长和宽分别是( )cm和( )cm。
三、判断题
17.周长相等的长方形和平行四边形的面积一定相等。( )
18.平行四边形的底增加2厘米,高减少2厘米后面积不变。( )
19.两个面积相等的直角梯形一定等底等高。( )
20.每个小方格是1cm2,洋洋估测“树叶”的面积是12cm2。( )
21.在一个长方形纸上剪下一个最大的三角形,三角形的面积是长方形面面积的一半。( )
四、图形计算
22.求如图图形的面积。(单位:厘米)
23.计算下列图形阴影部分的面积。(单位:cm)
五、解答题
24.有一块三角形的麦田,底275米,高60米,共收小麦19.8吨。这块麦田有多少公顷?平均每公顷收小麦多少吨?
25.某小区在靠墙边的一块空地上新建了一个近似梯形的花坛,围成花坛的篱笆全长是56米,其中近似高的一段长是20米(如图)。这个花坛的面积大约是多少?
26.爱民小学有一块校内劳动基地(如图)。学校把它分成一个平行四边形和一个三角形,平行四边形地里种大白菜,三角形地里种萝卜。
(1)每棵大白菜占地0.15平方米,一共可以种多少棵?
(2)萝卜地有多少平方米?
27.王伯伯有一块近似平行四边形的菜地,为了方便浇灌,中间留了一条小路。如果每平方米青菜能卖50元钱,这块地的青菜一共可以卖多少元?
28.一个梯形果园,上底长18米,比下底短5米,高16米。现在在这个果园里栽上梨树,每棵梨树占地4平方米。
(1)这个果园的面积多少平方米?
(2)这个果园可以栽多少棵梨树?
参考答案:
1.C
【分析】根据三角形的面积公式:S=ab÷2,由此可知a=2S÷b,用160乘2,再除以4计算即可。
【详解】160×2÷4
=320÷4
=80(米)
则它的底是80米。
故答案为:C
【点睛】本题考查三角形的面积,灵活运用三角形的面积公式是解题的关键。
2.A
【分析】长方形和正方形是特殊的平行四边形,两个完全一样的直角三角形可以拼成长方形,两个完全一样的等腰直角三角形可以拼成正方形。如图 ,两个完全一样的三角形一定可以拼成一个平行四边形。
【详解】A.两个完全一样的三角形一定可以拼成一个平行四边形;
B.如图 完全一样的三角形不能拼成长方形;
C.如图完全一样的三角形不能拼成正方形;
D.两个完全一样的三角形不能拼成梯形。
故答案为:A
【点睛】关键是熟悉平面图形的特征,拆拼图形时,考虑图形剪开后各部分的形状、大小、位置的关系。
3.A
【分析】根据图,甲、乙都是三角形,三角形的面积=底×高÷2。那么,选定合适的底和高,分析出甲、乙的面积关系即可。
【详解】以梯形的上底为甲的底,梯形的下底为乙的底,此时两个三角形的高相等。又因为,这个梯形的上底大于下底,所以甲的底大于乙的底,所以甲的面积大一些。
故答案为:A
【点睛】本题考查了三角形的面积,熟记面积公式是解题的关键。
4.B
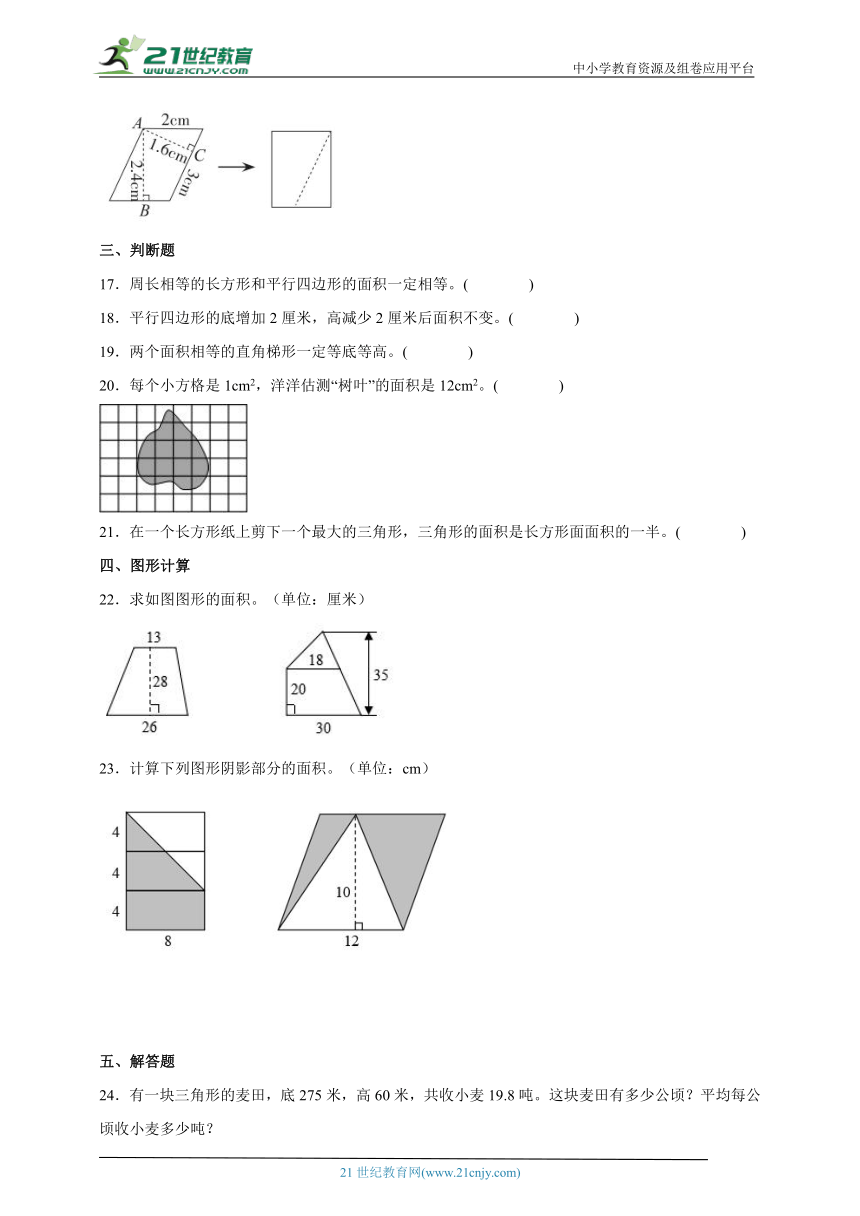
【分析】先根据“三角形的面积=底×高÷2”分别求出两个三角形的面积,再求出两个三角形的面积和。
【详解】如下图,设上面的三角形1厘米的底边所对应的高为,下面的三角形1厘米的底边所对应的高是厘米,则有+=8厘米。
上面的三角形的面积:1×÷2=÷2
下面的三角形的面积:1×÷2=÷2
两个三角形的面积和:÷2+÷2
=(+)÷2
=8÷2
=4(平方厘米)
故答案为:B
【点睛】明确两个三角形高的和与正方形边长的关系是解决此题的关键。
5.B
【分析】观察平行四边形可知,12cm的底对应的高是7.5cm,9cm的底对应的高是10cm,根据平行四边形的面积公式,可用12×7.5或9×10即可求出平行四边形的面积。
【详解】12×7.5=90(cm2)
9×10=90(cm2)
计算平行四边形面积的正确算式是12×7.5或9×10。
故答案为:B
【点睛】本题考查了平行四边形的面积公式的灵活应用,关键是找到底边对应的高。
6.C
【分析】把一个活动的平行四边形框架拉成一个长方形,四个边的长度没变,则其周长不变;根据长方形的面积=长×宽,平行四边形的面积=底×高, 长方形的长和原来平行四边形的底相等,长方形的宽大于原来平行四边形的高,所以长方形的面积比原来平行四边形的面积变大了。
【详解】如图:
把一个活动的平行四边形框架拉成一个长方形,周长不变;由于拉成的长方形的宽大于原来平行四边形的高,所以面积变大了。
故答案为:C
【点睛】掌握平行四边形拉成长方形后,长方形的长、宽分别与平行四边形的底和高之间的关系是解题的关键。
7.B
【分析】根据题意,在平行四边形内画一个最大的三角形,那么这个三角形与平行四边形等底等高;根据三角形的面积=底×高÷2,平行四边形的面积=底×高可知,等底等高的三角形的面积是平行四边形面积的一半,据此解答。
【详解】42÷2=21(平方米)
在面积为42平方米的平行四边形内画一个最大的三角形,这个三角形的面积是21平方米。
故答案为:B
【点睛】关键是明白在平行四边形内画一个最大的三角形,那么这个三角形与平行四边形等底等高,再利用等底等高的三角形的面积与平行四边形面积的关系解决问题。
8.A
【分析】根据选项中各图形的分割方法分别计算各组合图形的面积,最后找出和题目计算方法相同的选项,据此解答。
【详解】A.整个图形的面积=上面长方形的面积+下面长方形的面积。
(8-2)×4+12×2
=6×4+12×2
=24+24
=48
所以,组合图形的面积是48。
B.整个图形的面积=左边长方形的面积+右边长方形的面积。
8×4+(12-4)×2
=8×4+8×2
=32+16
=48
所以,组合图形的面积是48。
C.整个图形的面积=左边梯形的面积+右边梯形的面积。
(8-2+8)×4÷2+(12-4+12)×2÷2
=14×4÷2+20×2÷2
=28+20
=48
所以,组合图形的面积是48。
D.组合图形的面积=大长方形的面积-小长方形的面积。
12×8-(12-4)×(8-2)
=12×8-8×6
=96-48
=48
所以,组合图形的面积是48。
故答案为:A
【点睛】同一个图形的面积可能有多种不同的计算方法,掌握组合图形面积的计算方法是解答题目的关键。
9. 12+2a 6b
【分析】等腰三角形的周长是三条边长之和,根据等腰三角形的特征:两条腰是相等的;根据三角形面积=底×高÷2,代入相应数值即可完成解答。
【详解】12+a+a=12+2a(cm)
12×b÷2=6b(cm2)
所以这个等腰三角形的周长是(12+2a)cm,面积是(6b)cm2。
【点睛】解答本题的关键是掌握等腰三角形的面积及特征。
10.3.6
【分析】平行四边形的面积公式:平行四边形的面积=底×高,三角形的面积公式:三角形的面积=底×高÷2,已知三角形和平行四边形等底等高,这时三角形的面积是平行四边形面积的一半。据此解答。
【详解】7.2÷2=3.6(平方分米)
与平行四边形等底等高的三角形面积是3.6平方分米。
【点睛】本题考查了平行四边形和三角形面积之间的关系,需要明确平行四边形的面积是与它等底等高的三角形面积的2倍。
11. 6.4 40
【分析】(1)根据平行四边形的面积=底×高,先用8×4=32(cm2)求出平行四边形的面积,再用面积除以另一条底求出另一条底对应的高;
(2)将木框拉伸成长方形,那么平行四边形的一条底是长方形的长,另一条底是长方形的宽,根据长方形的面积=长×宽把数据代入求出长方形的面积。
【详解】8×4÷5
=32÷5
=6.4(cm)
8×5=40(cm2)
所以一个平行四边形木框的一条底是8cm,对应的高是4cm,另一条底是5cm,对应的高是6.4cm;将木框拉伸成长方形,那这个长方形的面积是40cm2。
【点睛】本题重点考查平行四边形和长方形的面积公式,明确拉伸过程中平行四边形和长方形的关系是解题的关键。
12. 4 24
【分析】如图:作出该梯形的另一条高,以这条高为界,右边是一个等腰直角三角形,所以该梯形的高是(8-4)cm;再根据梯形的面积公式:S=(a+b)h÷2,据此代入数值进行计算即可。
【详解】8-4=4(cm)
(4+8)×4÷2
=12×4÷2
=48÷2
=24(cm2)
则它的高应该是4cm,面积应该是24cm2。
【点睛】本题考查梯形的面积,熟记公式是解题的关键。
13.8
【分析】根据平行四边形面积公式的推导过程可知,把一个平行四边形割补成一个长方形,只是形状变了,面积不变,长方形的宽相当于平行四边形的高,长方形的长相当于平行四边形的底,已知长方形的面积是48cm2,长方形的宽是6cm,根据平行四边形的面积公式和长方形的面积公式,用48÷6即可求出原来平行四边形的底,据此解答。
【详解】48÷6=8(cm)
原平行四边形的底是8cm。
【点睛】本题主要考查平行四边形面积的推导过程,明确平行四边形无论割补成什么形状,面积没有发生变化。
14.94.5
【分析】一个直角梯形的上底不变,如果把下底减少3厘米,这个梯形就变成了正方形,可知这个梯形的上底是9厘米,下底是9+3=12厘米,高是9厘米,然后再根据梯形的面积公式进行计算。
【详解】9+3=12(厘米)
(9+12)×9÷2
=21×9÷2
=94.5(平方厘米)
即原梯形面积是94.5平方厘米。
【点睛】本题的主要考查了学生根据梯形的面积公式解答问题的能力,解答此题关键是求出下底的长,再根据公式求解。
15.18
【分析】因为三角形的面积S=ah÷2,平行四边形的面积S=ah,所以三角形的面积是与其等底等高的平行四边形的面积的一半;据此解答即可。
【详解】36÷2=18(平方厘米)
即三角形DEC的面积是18平方厘米。
【点睛】此题主要考查等底等高的三角形和平行四边形的面积的关系。
16. 2.4 2 3 1.6
【分析】根据平行四边形面积公式的推导过程可知,把一个平行四边形沿高AB剪开得到两部分,并把三角形部分向右平移与另一部分拼成一个长方形,拼成的长方形的长等于平行四边形的高,长方形的宽等于平行四边形的底。若沿高AC剪开得到的两部分,拼成的长方形的长等于平行四边形的底,长方形的宽等于平行四边形的高,据此解答。
【详解】在探索平行四边形面积计算公式时,小明同学沿着高AB剪开后,他拼成的长方形的长是2.4cm,宽是2cm。如果小红同学是沿着高AC剪拼的,她拼成的长方形的长是3cm,宽是1.6cm。
【点睛】解答本题的关键是理解掌握平行四边形面积公式的推导过程及应用。
17.×
【分析】长方形的面积=长×宽,平行四边形的面积=底×高,可假设长方形的长=平行四边形的底,长方形的宽=平行四边形的一条斜边,那么长方形的宽>平行四边形的高,所以长×宽>底×高,则长方形的面积>平行四边形的面积,故面积-定不相等。
【详解】由分析可知:周长相等的长方形和平行四边形的面积一定相等,说法错误。
故答案为:×
【点睛】本题考查了学生对平行四边形、长方形面积公式的理解和运用。
18.×
【分析】假设出原来平行四边形的底和高,平行四边形的面积=底×高,求出原来平行四边形的面积和现在平行四边形的面积,即可求得。
【详解】假设原来平行四边形的底为3厘米,高为4厘米。
原来平行四边形的面积:3×4=12(平方厘米)
现在平行四边形的面积:(3+2)×(4-2)
=5×2
=10(平方厘米)
因为12平方厘米≠10平方厘米,所以平行四边形的面积变了。
故答案为:×
【点睛】掌握平行四边形的面积计算公式是解答题目的关键。
19.×
【分析】通过梯形的面积公式,举例论证此说法是错误的。
【详解】梯形①面积是20,则上底2,下底8,高是4。
梯形②的面积也是20,则上底是1.5,下底3.5,高是8。
它们的面积相等,但是底和高不相等。
故答案为:×
【点睛】此题的解题关键是利用梯形面积公式,用举例的方式,进行论证,证明题干的说法是错误的。
20.√
【分析】首先把图形用方格划分,注意每一部分估算取整,其中不足1格的按照半格计算,最后合并即可得出答案。
【详解】有7个整格子,大约10个半方格,大约7+10÷2=12个方格,因为每个小方格的面积是1cm2,因此面积为12cm2。
故答案为:√
【点睛】解决此题的关键是利用割补法,把不规则的图形拼为规则的图形,进一步估算面积即可。
21.√
【分析】在长方形中剪出的最大三角形,它的底和长方形的长相等,高和长方形的宽相等。据此结合长方形和三角形的面积公式,推断和这个三角形和长方形的面积关系即可。
【详解】在一个长方形纸上剪下一个最大的三角形,三角形面积=长×宽÷2,长方形面积=长×宽,所以这个三角形的面积是长方形面面积的一半。
所以判断正确。
【点睛】本题考查了三角形和长方形的面积,熟记面积公式是解题的关键。
22.546平方厘米;615平方厘米
【分析】(1)梯形的上底为13厘米,下底为26厘米,高为28厘米,利用“梯形的面积=(上底+下底)×高÷2”求出梯形的面积;
(2)整个图形的面积=上面三角形的面积+下面梯形的面积,据此解答。
【详解】(1)(13+26)×28÷2
=39×28÷2
=1092÷2
=546(平方厘米)
所以,该图形的面积是546平方厘米。
(2)35-20=15(厘米)
18×15÷2+(18+30)×20÷2
=18×15÷2+48×20÷2
=270÷2+960÷2
=135+480
=615(平方厘米)
所以,该图形的面积是615平方厘米。
23.64cm2;60cm2
【分析】观察图形可知,第一个阴影部分是一个上底为4cm,下底为(4×3)cm,高为8cm的梯形,根据梯形的面积公式求解即可;
第二个阴影部分的面积等于一个底为12cm,高为10cm的平行四边形面积减去一个底为12cm,高为10cm的三角形面积,根据平行四边形的面积公式和三角形的面积公式求解即可。
【详解】4×3=12(cm)
(12+4)×8÷2
=16×8÷2
=128÷2
=64(cm2)
第一个阴影部分的面积是64cm2。
12×10-12×10÷2
=120-60
=60(cm2)
第二个阴影部分的面积是60cm2。
24.0.825公顷;24吨
【分析】根据三角形的面积=底×高÷2,代入相应数值计算,所得结果即为这块麦田的面积;要求平均每公顷收小麦多少吨,用小麦的总吨数除以这块麦田的面积,据此解答。
【详解】275×60÷2
=16500÷2
=8250(平方米)
8250平方米=0.825公顷
19.8÷0.825=24(吨)
答:这块麦田的有0.825公顷,平均每公顷收小麦24吨。
【点睛】解答本题的关键是掌握三角形面积的计算公式,同时要弄清谁是单一量,再用另一个量进行平均分。
25.360平方米
【分析】通过篱笆全长是56米与近似高为20米,可以求出上底与下底的和,再通过梯形的面积公式(上底+下底)×高÷2,即可求解。
【详解】(56-20)×20÷2
=36×20÷2
=720÷2
=360(平方米)
答:这个花坛的面积大约是360平方米。
【点睛】此题考查梯形的面积,解题关键为求到上下底的和,熟练掌握梯形的面积公式,即可解题。
26.(1)400棵;
(2)22.5平方米
【分析】(1)利用“平行四边形的面积=底×高”求出白菜地的面积,一共可以种白菜的棵数=白菜地的面积÷每棵白菜的占地面积;
(2)三角形的底为(14-8)米,三角形的高和平行四边形的高相等,利用“三角形的面积=底×高÷2”求出萝卜地的面积,据此解答。
【详解】(1)8×7.5÷0.15
=60÷0.15
=400(棵)
答:一共可以种400棵。
(2)(14-8)×7.5÷2
=6×7.5÷2
=45÷2
=22.5(平方米)
答:萝卜地有22.5平方米。
【点睛】掌握平行四边形和三角形的面积计算公式是解答题目的关键。
27.10000元
【分析】菜地面面积=原来菜地面积-中间小路的面积,通过图形的平移,菜地的面积可以看作是底为(21-1)米,高为10米的平行四边形面积,平行四边形面积=底×高,青菜可卖出的总价=菜地面积×每平方米青菜可卖钱数,据此解答。
【详解】(21-1)×10
=20×10
=200(平方米)
200×50=10000(元)
答:这块地的青菜一共可以卖10000元。
【点睛】本题考查平行四边形的面积公式以及根据总价、数量和单价之间的关系来解决问题。
28.(1)328平方米;
(2)82棵
【分析】(1)下底=上底+5米,求出下底,再根据梯形的面积=(上底+下底)×高÷2,代入数据,即可求出果园的面积。
(2)用果园的面积除以每棵梨树占地的面积,即可求出这个果园可以栽多少棵梨树。
【详解】(1)18+5=23(米)
(18+23)×16÷2
=41×16÷2
=328(平方米)
答:这个果园的面积是328平方米。
(2)328÷4=82(棵)
答:这个果园可以栽82棵梨树。
【点睛】此题的解题关键是灵活运用梯形的面积公式求解。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
