第一单元 简易方程整理与练习(课件)- 五年级下册数学 苏教版(共28张PPT)
文档属性
| 名称 | 第一单元 简易方程整理与练习(课件)- 五年级下册数学 苏教版(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-05 00:00:00 | ||
图片预览








文档简介
(共28张PPT)
整理与练习
苏教版 五年级下册
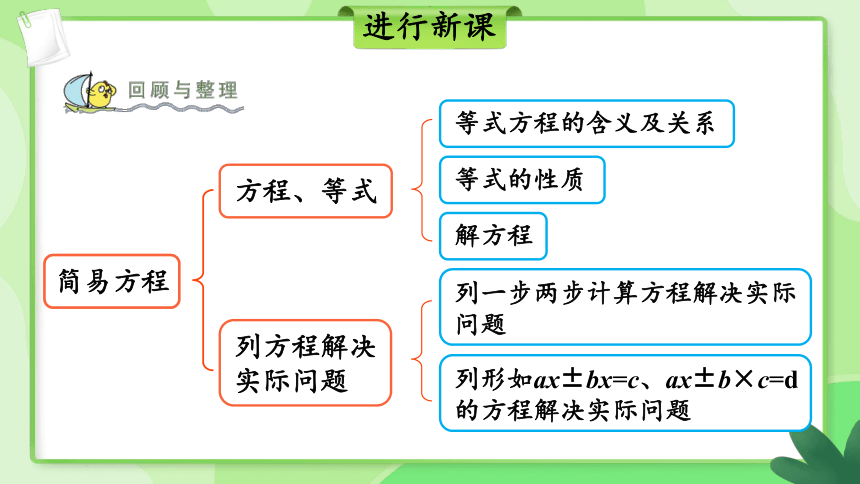
简易方程
方程、等式
列方程解决实际问题
等式方程的含义及关系
等式的性质
解方程
列一步两步计算方程解决实际问题
列形如ax±bx=c、ax±b×c=d的方程解决实际问题
进行新课
小组讨论:
1.举例说说方程、方程的解和解方程的含义。
含有未知数的等式是方程。
使方程左右两边相等的未知数的值叫作方程的解。
求方程的解的过程叫作解方程。
方程中的未知数不一定用x表示,也可用其他字母表示。
等式和方程的关系可表示如右图:
使方程左右两边相等的未知数的值叫作方程的解。
求方程的解的过程叫作解方程。
3 x + 6 = 12
解: 3 x = 6
x = 2
……方程
……方程的解
解方程
小组讨论:
2.等式有哪些性质?用等式的性质解方程时要注意什么?
等式的性质(1)
等式两边同时加上或减去同一个数, 所得结果仍然是等式。
等式的性质(2):
等式两边同时乘或除以同一个不是 0 的数, 所得结果仍然是等式。
我们在用等式的性质解方程时要根据原方程的特点,在方程两边同时进行加、减、乘、除的运算。
小组讨论:
2.等式有哪些性质?用等式的性质解方程时要注意什么?
小组讨论:
3.列方程解决实际问题一般经过哪些步骤?
列方程解决实际问题的一般步骤:
(1)设未知数;
(2)找出题目中的等量关系;
(3)列方程;
(4)解方程;
(5)检验;
(6)作答。
设
找
列
解
检
答
小红的体重+2.5 = 36
①寻找关键句,把语言转换成等量关系。
②根据常用数量关系式或公式写等量关系。
③根据结构特征找等量关系,如和倍(差倍)问题。
小组讨论:
4.怎样找到数量之间的相等关系?
(1)相差关系的实际问题,有两种列方程的方法,即x ±a=b
和b± x =a的形式;
(2)倍数关系的实际问题,通常依据“一倍数×倍数=几倍数”
或“几倍数÷倍数=一倍数”列方程。
(3)甲比乙的几倍多(或少)几,已知甲,求乙的问题,可
设乙为x ,根据乙×倍数±几=甲,列出形如ax±b=c的方
程进行求解。
小组讨论:
4.实际应用中可能存在哪些等量关系式?
1.下面哪些式子是方程?
x + 2.4 = 5
15÷b
3x + 4x = 28
6n<3.6
90-a = 40
4y = 0.4
4.9-3.7 = 1.2
2a-5b = 3
√
√
√
√
√
一个式子是方程需符合两个条件:①是等式;②含有未知数。
课堂演练
【选自教材P18 练习与应用 第1题】
解:0.6+x-0.6 = 2.7-0.6
x = 2.1
解:x-35+35 = 95+35
x = 130
解:180+6 x-180 = 330-180
6 x = 150
解:14x÷14 = 7÷14
x = 0.5
0.6+ x = 2.7
2.解方程。
x - 35 = 95
180+6 x = 330
14 x = 7
x = 25
【选自教材P18 练习与应用 第2题】
解: x÷15×15 = 180×15
x = 2700
2.解方程。
x ÷ 15 = 180
x -0.8 x = 10
解: 0.2 x = 10
0.2x÷0.2 = 10÷0.2
x = 50
【选自教材P18 练习与应用 第2题】
长方形的面积=长×宽
3. 一卷塑料薄膜展开后,正好可以
铺满一块30m2的长方形秧田。这
卷薄膜展开后有多长?
解:设这卷薄膜展开后有x米长。
1.5 x = 30
x = 30÷1.5
x = 20
答:这卷薄膜展开后有20米长。
【选自教材P18 练习与应用 第3题】
4. 世界人均土地面积大约是2.34公顷,相当于我国人均
土地面积的3倍。我国人均土地面积大约是多少公顷?
解:设我国人均土地面积大约是x公顷。
3 x = 2.34
x = 2.34÷3
x = 0.78
答:我国人均土地面积大约是0.78公顷。
世界人均土地面积=我国人均土地面积×3
标准量(1倍量)
【选自教材P18 练习与应用 第4题】
解:设武汉长江大桥铁路桥长x米,公路桥长y米。
5x +197 = 6772
5x = 6575
x = 1315
答:武汉长江大桥铁路桥长1315米,公路桥长1670米。
5. 南京长江大桥铁路桥长6772米,公路桥长4589米。它的铁路桥比武汉长江大桥铁路桥的5倍多197米,公路桥比武汉长江大桥公路桥的3倍少421米。武汉长江大桥铁路桥和公路桥各长多少米?
3y -421 = 4589
3y = 5010
y = 1670
南京长江天桥铁路桥长=武汉长江大桥铁路桥×5+197
南京长江大桥公路桥长=武汉长江大桥公路桥长×3-421
【选自教材P19 练习与应用 第5题】
6.学校印制画册一共用去2240元,画册的印刷费是3.6元/本,
其余费用是800元。学校印制了多少本画册?
解:设学校印制了x本画册。
3.6x +800 = 2240
3.6x = 1440
x = 400
答:学校印制了400本画册。
印刷总费用=每本印刷费用×本数
【选自教材P19 练习与应用 第6题】
解: 58x = 145
x = 2.5
解: 2.2x -1= 10
2.2x = 11
x = 5
解:4.5+2 x = 11.5
2 x = 7
7.解方程。
27 x +31 x = 145
2.2 x -0.5×2 = 10
3×1.5+2 x = 11.5
13 x - 7 x = 5.7
解: 6x = 5.7
x = 0.95
x = 3.5
【选自教材P19 练习与应用 第7题】
8. 猎豹追捕猎物时的速度大约是优秀短跑运动员百米赛
跑速度的3倍,每秒大约比运动员多跑20米。优秀短
跑运动员每秒大约跑多少米?猎豹呢?
解:设优秀短跑运动员每秒大约跑x米,则猎豹每秒大约跑3 x米。
3x - x = 20
2x = 20
x = 10
答:优秀短跑运动员每秒大约跑10米,则猎豹每秒大约跑30米。
3x = 3×10=30
猎豹每秒跑的距离-运动员每秒跑的距离=20
标准量(1倍量)
【选自教材P19 练习与应用 第8题】
9. 甲、乙两个工程队合开一条720米长的隧道,同时各
从一端开凿,经过24天开通。甲队每天开凿 14.5 米,
乙队每天开凿多少米?
解:设乙队每天开凿x米。
24x +14.5×24 = 720
24x +348 = 720
24x = 372
答:设乙队每天开凿15.5米。
x = 15.5
(x +14.5)×24 = 720
x +14.5 = 720÷24
x +14.5 = 30
x = 15.5
甲队开凿的米数+乙队开凿的米数=720
甲、乙两队每天开凿的米数和×天数=720
【选自教材P19 练习与应用 第9题】
解:设每张光盘x元。
8x + 10x = 216
18x = 216
x = 12
答:每张光盘12元。
(8+ 10)x = 216
18x = 216
x = 12
10张光盘的价钱+8张光盘的价钱=216
每张光盘的价钱×两人买的光盘总张数= 216
【选自教材P19 练习与应用 第10题】
11. 学校体育室一共有186根跳绳。四年级5个班,每班借了
18根。剩下的借给五年级的4个班,平均每班借多少根?
解:设平均每班借了x根。
4x +5×18 = 186
4x +90 = 186
4x = 96
答:平均每班借了24根。
四年级借的跳绳根数+五年级借的跳绳根数=186
x = 24
【选自教材P19 练习与应用 第11题】
12.
解:设每张门票x元。
145x - 132x = 65
13x = 65
x = 5
答:每张门票5元。
(145-132) x = 65
13x = 65
x = 5
五年级买门票的价钱-四年级买门票的价钱=65
五年级比四年级多的人数×每张门票价格=65
【选自教材P19 练习与应用 第12题】
点击图片
13. 把下面的线段分成两段,使其中一段的长是另一段的4倍。
提示:先量出线段的长度,再根据和倍问题的解题方法或列方程解答求出两段的长度,最后将线段分段。
【选自教材P20 探索与实践 第13题】
(1)观察上表,你有什么发现?在小组里交流。
(2)你会用含有b的式子表示a或c吗?表示a、b、c的和呢?
14. 下表中的a、b、c表示3个连续的自然数。任意写出
三组这样的数,并求出各组数的和。
每相邻两个自然数,后一个数比前一个数多1。
提示:发现a+b+c= 3b是解决此问题的关键。
【选自教材P20 探索与实践 第14题】
提示:设中间的一个数是x,再利用发现的规律列方程解答。
(3)如果3个连续自然数的和是99,你能列方程求出这3个数各
是多少吗?
解:设这3个连续自然数中间的数是x,则第1个数为x -1,第2个数为x +1。
3x = 99
x = 33
x -1= 33-1=32
答:这3个连续自然数是32、33、34。
x +1= 33+1=34
【选自教材P20 探索与实践 第14题】
15.
你会和同学一起玩这个游戏吗?
一个数×3-2
6×3-2=16
【选自教材P20 探索与实践 第15题】
通过这节课的学习活动,你有什么收获?
课堂小结
整理与练习
苏教版 五年级下册
简易方程
方程、等式
列方程解决实际问题
等式方程的含义及关系
等式的性质
解方程
列一步两步计算方程解决实际问题
列形如ax±bx=c、ax±b×c=d的方程解决实际问题
进行新课
小组讨论:
1.举例说说方程、方程的解和解方程的含义。
含有未知数的等式是方程。
使方程左右两边相等的未知数的值叫作方程的解。
求方程的解的过程叫作解方程。
方程中的未知数不一定用x表示,也可用其他字母表示。
等式和方程的关系可表示如右图:
使方程左右两边相等的未知数的值叫作方程的解。
求方程的解的过程叫作解方程。
3 x + 6 = 12
解: 3 x = 6
x = 2
……方程
……方程的解
解方程
小组讨论:
2.等式有哪些性质?用等式的性质解方程时要注意什么?
等式的性质(1)
等式两边同时加上或减去同一个数, 所得结果仍然是等式。
等式的性质(2):
等式两边同时乘或除以同一个不是 0 的数, 所得结果仍然是等式。
我们在用等式的性质解方程时要根据原方程的特点,在方程两边同时进行加、减、乘、除的运算。
小组讨论:
2.等式有哪些性质?用等式的性质解方程时要注意什么?
小组讨论:
3.列方程解决实际问题一般经过哪些步骤?
列方程解决实际问题的一般步骤:
(1)设未知数;
(2)找出题目中的等量关系;
(3)列方程;
(4)解方程;
(5)检验;
(6)作答。
设
找
列
解
检
答
小红的体重+2.5 = 36
①寻找关键句,把语言转换成等量关系。
②根据常用数量关系式或公式写等量关系。
③根据结构特征找等量关系,如和倍(差倍)问题。
小组讨论:
4.怎样找到数量之间的相等关系?
(1)相差关系的实际问题,有两种列方程的方法,即x ±a=b
和b± x =a的形式;
(2)倍数关系的实际问题,通常依据“一倍数×倍数=几倍数”
或“几倍数÷倍数=一倍数”列方程。
(3)甲比乙的几倍多(或少)几,已知甲,求乙的问题,可
设乙为x ,根据乙×倍数±几=甲,列出形如ax±b=c的方
程进行求解。
小组讨论:
4.实际应用中可能存在哪些等量关系式?
1.下面哪些式子是方程?
x + 2.4 = 5
15÷b
3x + 4x = 28
6n<3.6
90-a = 40
4y = 0.4
4.9-3.7 = 1.2
2a-5b = 3
√
√
√
√
√
一个式子是方程需符合两个条件:①是等式;②含有未知数。
课堂演练
【选自教材P18 练习与应用 第1题】
解:0.6+x-0.6 = 2.7-0.6
x = 2.1
解:x-35+35 = 95+35
x = 130
解:180+6 x-180 = 330-180
6 x = 150
解:14x÷14 = 7÷14
x = 0.5
0.6+ x = 2.7
2.解方程。
x - 35 = 95
180+6 x = 330
14 x = 7
x = 25
【选自教材P18 练习与应用 第2题】
解: x÷15×15 = 180×15
x = 2700
2.解方程。
x ÷ 15 = 180
x -0.8 x = 10
解: 0.2 x = 10
0.2x÷0.2 = 10÷0.2
x = 50
【选自教材P18 练习与应用 第2题】
长方形的面积=长×宽
3. 一卷塑料薄膜展开后,正好可以
铺满一块30m2的长方形秧田。这
卷薄膜展开后有多长?
解:设这卷薄膜展开后有x米长。
1.5 x = 30
x = 30÷1.5
x = 20
答:这卷薄膜展开后有20米长。
【选自教材P18 练习与应用 第3题】
4. 世界人均土地面积大约是2.34公顷,相当于我国人均
土地面积的3倍。我国人均土地面积大约是多少公顷?
解:设我国人均土地面积大约是x公顷。
3 x = 2.34
x = 2.34÷3
x = 0.78
答:我国人均土地面积大约是0.78公顷。
世界人均土地面积=我国人均土地面积×3
标准量(1倍量)
【选自教材P18 练习与应用 第4题】
解:设武汉长江大桥铁路桥长x米,公路桥长y米。
5x +197 = 6772
5x = 6575
x = 1315
答:武汉长江大桥铁路桥长1315米,公路桥长1670米。
5. 南京长江大桥铁路桥长6772米,公路桥长4589米。它的铁路桥比武汉长江大桥铁路桥的5倍多197米,公路桥比武汉长江大桥公路桥的3倍少421米。武汉长江大桥铁路桥和公路桥各长多少米?
3y -421 = 4589
3y = 5010
y = 1670
南京长江天桥铁路桥长=武汉长江大桥铁路桥×5+197
南京长江大桥公路桥长=武汉长江大桥公路桥长×3-421
【选自教材P19 练习与应用 第5题】
6.学校印制画册一共用去2240元,画册的印刷费是3.6元/本,
其余费用是800元。学校印制了多少本画册?
解:设学校印制了x本画册。
3.6x +800 = 2240
3.6x = 1440
x = 400
答:学校印制了400本画册。
印刷总费用=每本印刷费用×本数
【选自教材P19 练习与应用 第6题】
解: 58x = 145
x = 2.5
解: 2.2x -1= 10
2.2x = 11
x = 5
解:4.5+2 x = 11.5
2 x = 7
7.解方程。
27 x +31 x = 145
2.2 x -0.5×2 = 10
3×1.5+2 x = 11.5
13 x - 7 x = 5.7
解: 6x = 5.7
x = 0.95
x = 3.5
【选自教材P19 练习与应用 第7题】
8. 猎豹追捕猎物时的速度大约是优秀短跑运动员百米赛
跑速度的3倍,每秒大约比运动员多跑20米。优秀短
跑运动员每秒大约跑多少米?猎豹呢?
解:设优秀短跑运动员每秒大约跑x米,则猎豹每秒大约跑3 x米。
3x - x = 20
2x = 20
x = 10
答:优秀短跑运动员每秒大约跑10米,则猎豹每秒大约跑30米。
3x = 3×10=30
猎豹每秒跑的距离-运动员每秒跑的距离=20
标准量(1倍量)
【选自教材P19 练习与应用 第8题】
9. 甲、乙两个工程队合开一条720米长的隧道,同时各
从一端开凿,经过24天开通。甲队每天开凿 14.5 米,
乙队每天开凿多少米?
解:设乙队每天开凿x米。
24x +14.5×24 = 720
24x +348 = 720
24x = 372
答:设乙队每天开凿15.5米。
x = 15.5
(x +14.5)×24 = 720
x +14.5 = 720÷24
x +14.5 = 30
x = 15.5
甲队开凿的米数+乙队开凿的米数=720
甲、乙两队每天开凿的米数和×天数=720
【选自教材P19 练习与应用 第9题】
解:设每张光盘x元。
8x + 10x = 216
18x = 216
x = 12
答:每张光盘12元。
(8+ 10)x = 216
18x = 216
x = 12
10张光盘的价钱+8张光盘的价钱=216
每张光盘的价钱×两人买的光盘总张数= 216
【选自教材P19 练习与应用 第10题】
11. 学校体育室一共有186根跳绳。四年级5个班,每班借了
18根。剩下的借给五年级的4个班,平均每班借多少根?
解:设平均每班借了x根。
4x +5×18 = 186
4x +90 = 186
4x = 96
答:平均每班借了24根。
四年级借的跳绳根数+五年级借的跳绳根数=186
x = 24
【选自教材P19 练习与应用 第11题】
12.
解:设每张门票x元。
145x - 132x = 65
13x = 65
x = 5
答:每张门票5元。
(145-132) x = 65
13x = 65
x = 5
五年级买门票的价钱-四年级买门票的价钱=65
五年级比四年级多的人数×每张门票价格=65
【选自教材P19 练习与应用 第12题】
点击图片
13. 把下面的线段分成两段,使其中一段的长是另一段的4倍。
提示:先量出线段的长度,再根据和倍问题的解题方法或列方程解答求出两段的长度,最后将线段分段。
【选自教材P20 探索与实践 第13题】
(1)观察上表,你有什么发现?在小组里交流。
(2)你会用含有b的式子表示a或c吗?表示a、b、c的和呢?
14. 下表中的a、b、c表示3个连续的自然数。任意写出
三组这样的数,并求出各组数的和。
每相邻两个自然数,后一个数比前一个数多1。
提示:发现a+b+c= 3b是解决此问题的关键。
【选自教材P20 探索与实践 第14题】
提示:设中间的一个数是x,再利用发现的规律列方程解答。
(3)如果3个连续自然数的和是99,你能列方程求出这3个数各
是多少吗?
解:设这3个连续自然数中间的数是x,则第1个数为x -1,第2个数为x +1。
3x = 99
x = 33
x -1= 33-1=32
答:这3个连续自然数是32、33、34。
x +1= 33+1=34
【选自教材P20 探索与实践 第14题】
15.
你会和同学一起玩这个游戏吗?
一个数×3-2
6×3-2=16
【选自教材P20 探索与实践 第15题】
通过这节课的学习活动,你有什么收获?
课堂小结
