3.5 质因数和分解质因数(课件)-五年级下册数学苏教版(共20张PPT)
文档属性
| 名称 | 3.5 质因数和分解质因数(课件)-五年级下册数学苏教版(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-05 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
质因数和分解质因数
苏教版五年级下册
三 因数与倍数
知识回顾
下面各数,哪些是质数,哪些是合数?
5 8 11 19 28 43 51
质数
合数
5 11 19 43
8 28 51
在 5 = 1×5、28 = 4×7 中,哪些数是 5 的因数?哪些数是 28 的因数?在这些因数中,哪几个数是质数?
探索新知
5 = 1 × 5,1 和 5是 5 的因数。
28 = 4 × 7,4 和 7
是 28 的因数。
在 1、5、4、7 中,
5 和 7 是质数。
如果一个数的因数是质数,这个因数就是它的质因数。
在 5 = 1×5、28 = 4×7 中,哪些数是 5 的因数?哪些数是 28 的因数?在这些因数中,哪几个数是质数?
上面的算式中, 哪个数是哪个数的质因数?
5 是 5 的质因数,7 是 28 的质因数。
归纳:判断一个数的因数是不是它的质因数,要依据因数本身是不是质数来确定。
探索新知
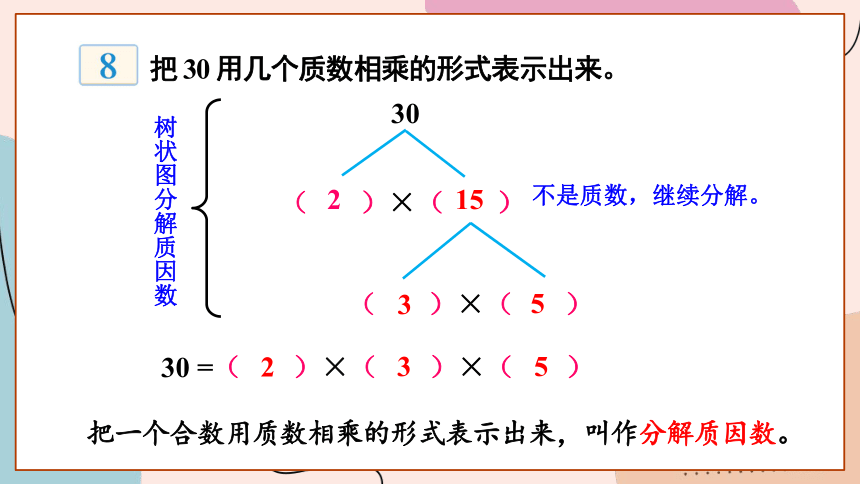
把 30 用几个质数相乘的形式表示出来。
( )×( )
30
( )×( )
2
15
3
5
30 =( )×( )×( )
2
3
5
不是质数,继续分解。
把一个合数用质数相乘的形式表示出来,叫作分解质因数。
树状图分解质因数
归纳:用树状图法分解质因数的方法:把合数
拆成两数相乘,如果因数是合数则继续拆分,
直到所有的因数都是质数为止。
把 6 和 14 分解质因数。
6 =( )×( ) 14 =( )×( )
2 3
2 7
易错点:分解质因数的结果不能写成乘法算式形式,且因数中不能有 1。如:14 分解质因数不能写成 2×7 = 14 或 1×2×7 = 14。
人们经常用短除法来分解质因数。
3 0
1 5
5
2
3
……先除以质数 2
……再除以质数 3
……除到商是质数为止
把每个除数和最后的商写成连乘的形式:30 = 2 ×3 ×5。
达标检测
【选自教材P39 练习六 第3题】
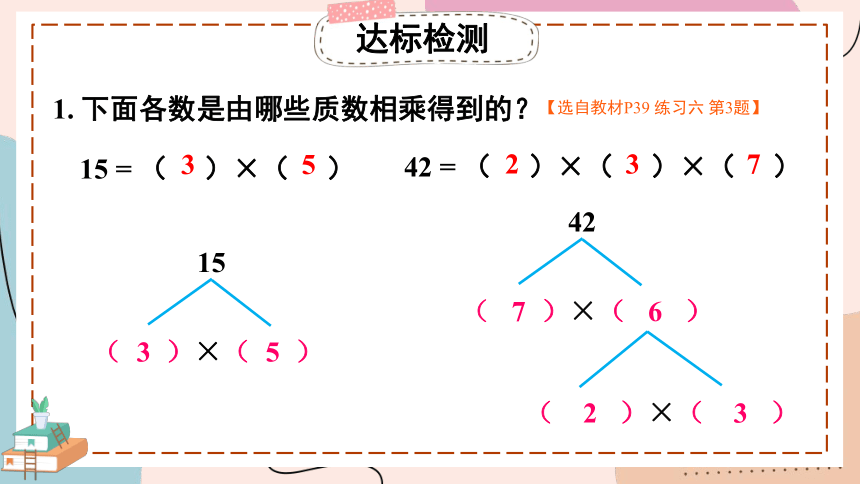
1. 下面各数是由哪些质数相乘得到的?
15 = ( )×( )
42 = ( )×( )×( )
15
( 3 )×( 5 )
3 5
( 2 )×( 3 )
42
( 7 )×( 6 )
2 3 7
26 = ( )×( )
66 = ( )×( )×( )
【选自教材P39 练习六 第3题】
1. 下面各数是由哪些质数相乘得到的?
2 6
1 3
2
6 6
3 3
1 1
2
3
2 13
2 3 11
达标检测
【选自教材P39 练习六 第4题】
2.(1)35 = 5×7,5 和 7 都是 35 的因数吗?都是 35 的
质因数吗?为什么?
(2)27 = 3×9,3 和 9 都是 27 的因数吗?都是 27 的
质因数吗?为什么?
5 和 7 都是 35 的因数,因为 5 和 7 都是质数,所以 5 和 7 都是 35 的质因数。
3 和 9 都是 27 的因数,3 是质数,所以 3 是 27 的质因数,9 是合数,所以 9 不是 27 的质因数。
3. 先圈出下面的合数,再把它们分解质因数。
7 9 13 16 20 25 29
【选自教材P39 练习六 第5题】
9
3
3
9 = 3×3
1 6
8
4
2
2
2
2
16 = 2×2×2×2
( 2 )×( 5 )
20
( 2 )×( 10 )
20 = 2×2×5
25
( 5 )×( 5 )
25 = 5×5
4. 找出下面每组数中的质数。
(1)13,23,33,43。
(2)5,15,25,35。
(3)17,27,37,47。
(4)19,29,39,49。
【选自教材P39 练习六 第6题】
易错点:判断一个数是否是质数,关键看这个数的因数个数,而不是看这个数个位上的数字。
5. 你会在括号里填合适的质数吗?
10 =( )×( ) 10 =( )+( )
14 =( )×( ) 14 =( )+( )
18 =( )×( )×( )
18 =( )+( )=( )+( )
【选自教材P40 练习六 第7题】
2 5
3 7
5 5
2 7
3 11
7 7
2 3 3
5 13 7 11
归纳:任何一个大于 4 的偶数都可以写成两个奇质数之和。
6. 下面哪几个班的学生可以分成人数相同的几个小组?
哪几个班不可以?为什么?
【选自教材P40 练习六 第8题】
一班、三班可以,二班、四班不可以。 因为39 和 40 是合数,41 和 43 是质数,质数不能分解成两个数(除 1 和它本身)相乘的形式。
易错点:分组不包含“每组 1 人”的特殊情况。
1. 下面这些数可以写成两个质数相加的形式吗?
思 考
1
3
5
7
9
11
13
15
不能
不能
= 2 + 3
= 2 + 5
= 2 + 7
不能
= 2 + 11
= 2 + 13
奇数
2. 下面这些数可以写成两个质数相加的形式吗?
2
4
6
8
10
12
14
16
不能
= 2 + 2
= 3 + 3
= 3 + 5
= 3 + 7
= 5 + 5
= 5 + 7
= 3 + 11
= 7 + 7
= 3 + 13
= 5 + 11
偶数
200 多年前,德国的数学家哥德巴赫发现每一个大于4 的偶数都可以表示成两个奇素数之和,例如,6 = 3 +3,8 = 3 +5,10 = 5 +5,12 = 5 +7。通过举例检验是完全可信的,但他却无法在理论上加以证明。于是,哥德巴赫于 1742 年 6 月 7 日写信给当时世界上最优秀的大数学家欧拉,请他帮助解决这个问题。欧拉回信表示:这个问题我虽然不能证明,但我确信它是正确的。同时,欧拉又补充指出:任何大于 2 的偶数都是两个素数之和。后来,这两个命题被合称为“哥德巴赫猜想”。
你知道吗
人们通常把数学誉为科学的皇后,而数论(研究自然数性质的数学分支)是数学的皇冠。由于哥德巴赫猜想的证明难度实在太高了,人们把这个猜想比喻为“数学皇冠上的明珠”。在摘取“明珠”的过程中,我国数学家做出了重要的贡献。1958~1962 年,王元和潘承洞的研究取得了重大进展。1966 年,陈景润更上一层楼,在“哥德巴赫猜想”的研究上取得了更加显著的进展,轰动了国内外数学界。他的研究成果被公认为最具有突破性和创造性,“是当代在哥德巴赫猜想的研究方面最好的成果”。
课堂小结
这节课你们都学会了哪些知识?
1. 一个数的因数是质数,这个因数就是它的质因数。
2. 把一个合数用质数相乘的形式表示出来,叫作分解质因数。
3. 可以用树状图法或短除法分解质因数。
质因数和分解质因数
苏教版五年级下册
三 因数与倍数
知识回顾
下面各数,哪些是质数,哪些是合数?
5 8 11 19 28 43 51
质数
合数
5 11 19 43
8 28 51
在 5 = 1×5、28 = 4×7 中,哪些数是 5 的因数?哪些数是 28 的因数?在这些因数中,哪几个数是质数?
探索新知
5 = 1 × 5,1 和 5是 5 的因数。
28 = 4 × 7,4 和 7
是 28 的因数。
在 1、5、4、7 中,
5 和 7 是质数。
如果一个数的因数是质数,这个因数就是它的质因数。
在 5 = 1×5、28 = 4×7 中,哪些数是 5 的因数?哪些数是 28 的因数?在这些因数中,哪几个数是质数?
上面的算式中, 哪个数是哪个数的质因数?
5 是 5 的质因数,7 是 28 的质因数。
归纳:判断一个数的因数是不是它的质因数,要依据因数本身是不是质数来确定。
探索新知
把 30 用几个质数相乘的形式表示出来。
( )×( )
30
( )×( )
2
15
3
5
30 =( )×( )×( )
2
3
5
不是质数,继续分解。
把一个合数用质数相乘的形式表示出来,叫作分解质因数。
树状图分解质因数
归纳:用树状图法分解质因数的方法:把合数
拆成两数相乘,如果因数是合数则继续拆分,
直到所有的因数都是质数为止。
把 6 和 14 分解质因数。
6 =( )×( ) 14 =( )×( )
2 3
2 7
易错点:分解质因数的结果不能写成乘法算式形式,且因数中不能有 1。如:14 分解质因数不能写成 2×7 = 14 或 1×2×7 = 14。
人们经常用短除法来分解质因数。
3 0
1 5
5
2
3
……先除以质数 2
……再除以质数 3
……除到商是质数为止
把每个除数和最后的商写成连乘的形式:30 = 2 ×3 ×5。
达标检测
【选自教材P39 练习六 第3题】
1. 下面各数是由哪些质数相乘得到的?
15 = ( )×( )
42 = ( )×( )×( )
15
( 3 )×( 5 )
3 5
( 2 )×( 3 )
42
( 7 )×( 6 )
2 3 7
26 = ( )×( )
66 = ( )×( )×( )
【选自教材P39 练习六 第3题】
1. 下面各数是由哪些质数相乘得到的?
2 6
1 3
2
6 6
3 3
1 1
2
3
2 13
2 3 11
达标检测
【选自教材P39 练习六 第4题】
2.(1)35 = 5×7,5 和 7 都是 35 的因数吗?都是 35 的
质因数吗?为什么?
(2)27 = 3×9,3 和 9 都是 27 的因数吗?都是 27 的
质因数吗?为什么?
5 和 7 都是 35 的因数,因为 5 和 7 都是质数,所以 5 和 7 都是 35 的质因数。
3 和 9 都是 27 的因数,3 是质数,所以 3 是 27 的质因数,9 是合数,所以 9 不是 27 的质因数。
3. 先圈出下面的合数,再把它们分解质因数。
7 9 13 16 20 25 29
【选自教材P39 练习六 第5题】
9
3
3
9 = 3×3
1 6
8
4
2
2
2
2
16 = 2×2×2×2
( 2 )×( 5 )
20
( 2 )×( 10 )
20 = 2×2×5
25
( 5 )×( 5 )
25 = 5×5
4. 找出下面每组数中的质数。
(1)13,23,33,43。
(2)5,15,25,35。
(3)17,27,37,47。
(4)19,29,39,49。
【选自教材P39 练习六 第6题】
易错点:判断一个数是否是质数,关键看这个数的因数个数,而不是看这个数个位上的数字。
5. 你会在括号里填合适的质数吗?
10 =( )×( ) 10 =( )+( )
14 =( )×( ) 14 =( )+( )
18 =( )×( )×( )
18 =( )+( )=( )+( )
【选自教材P40 练习六 第7题】
2 5
3 7
5 5
2 7
3 11
7 7
2 3 3
5 13 7 11
归纳:任何一个大于 4 的偶数都可以写成两个奇质数之和。
6. 下面哪几个班的学生可以分成人数相同的几个小组?
哪几个班不可以?为什么?
【选自教材P40 练习六 第8题】
一班、三班可以,二班、四班不可以。 因为39 和 40 是合数,41 和 43 是质数,质数不能分解成两个数(除 1 和它本身)相乘的形式。
易错点:分组不包含“每组 1 人”的特殊情况。
1. 下面这些数可以写成两个质数相加的形式吗?
思 考
1
3
5
7
9
11
13
15
不能
不能
= 2 + 3
= 2 + 5
= 2 + 7
不能
= 2 + 11
= 2 + 13
奇数
2. 下面这些数可以写成两个质数相加的形式吗?
2
4
6
8
10
12
14
16
不能
= 2 + 2
= 3 + 3
= 3 + 5
= 3 + 7
= 5 + 5
= 5 + 7
= 3 + 11
= 7 + 7
= 3 + 13
= 5 + 11
偶数
200 多年前,德国的数学家哥德巴赫发现每一个大于4 的偶数都可以表示成两个奇素数之和,例如,6 = 3 +3,8 = 3 +5,10 = 5 +5,12 = 5 +7。通过举例检验是完全可信的,但他却无法在理论上加以证明。于是,哥德巴赫于 1742 年 6 月 7 日写信给当时世界上最优秀的大数学家欧拉,请他帮助解决这个问题。欧拉回信表示:这个问题我虽然不能证明,但我确信它是正确的。同时,欧拉又补充指出:任何大于 2 的偶数都是两个素数之和。后来,这两个命题被合称为“哥德巴赫猜想”。
你知道吗
人们通常把数学誉为科学的皇后,而数论(研究自然数性质的数学分支)是数学的皇冠。由于哥德巴赫猜想的证明难度实在太高了,人们把这个猜想比喻为“数学皇冠上的明珠”。在摘取“明珠”的过程中,我国数学家做出了重要的贡献。1958~1962 年,王元和潘承洞的研究取得了重大进展。1966 年,陈景润更上一层楼,在“哥德巴赫猜想”的研究上取得了更加显著的进展,轰动了国内外数学界。他的研究成果被公认为最具有突破性和创造性,“是当代在哥德巴赫猜想的研究方面最好的成果”。
课堂小结
这节课你们都学会了哪些知识?
1. 一个数的因数是质数,这个因数就是它的质因数。
2. 把一个合数用质数相乘的形式表示出来,叫作分解质因数。
3. 可以用树状图法或短除法分解质因数。
