7.2 解决问题的策略(2)(课件)——五年级下册数学苏教版(共20张PPT)
文档属性
| 名称 | 7.2 解决问题的策略(2)(课件)——五年级下册数学苏教版(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-05 00:00:00 | ||
图片预览



文档简介
(共20张PPT)
解决问题的策略(2)
苏教版五年级下册
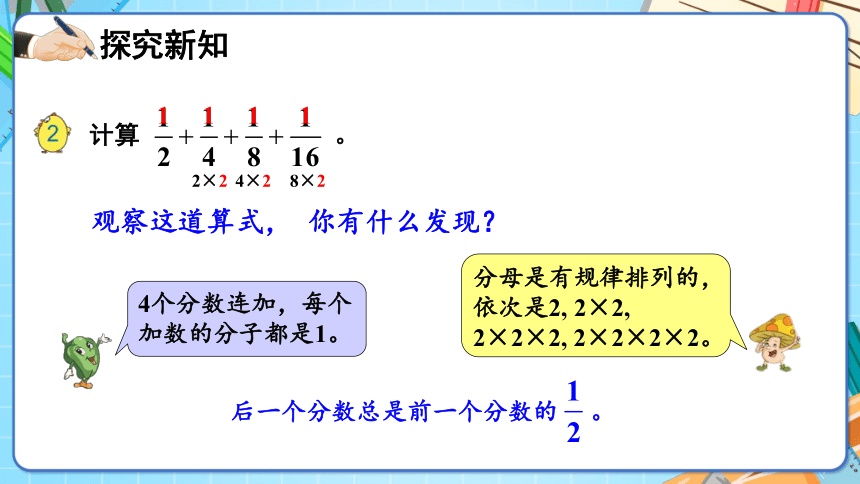
4个分数连加,每个加数的分子都是1。
分母是有规律排列的,依次是2, 2×2,
2×2×2, 2×2×2×2。
观察这道算式, 你有什么发现?
计算 。
1
1
1
1
2×2
4×2
8×2
后一个分数总是前一个分数的 。
探究新知
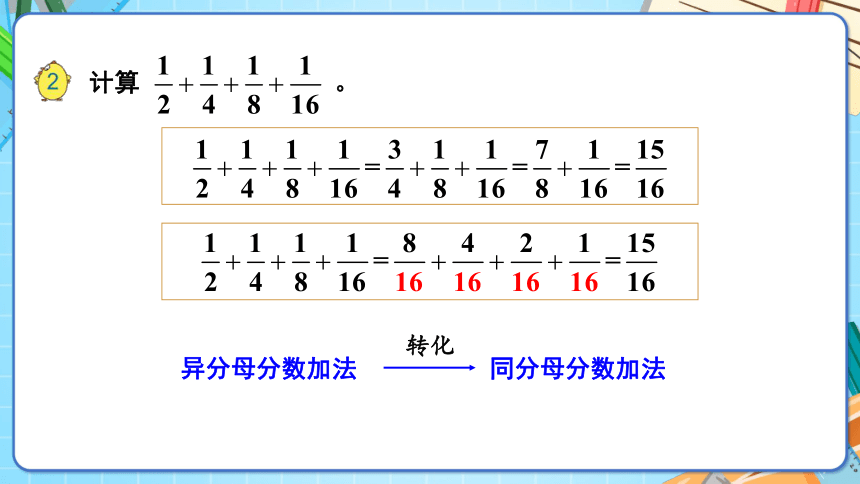
计算 。
异分母分数加法
转化
同分母分数加法
计算 。
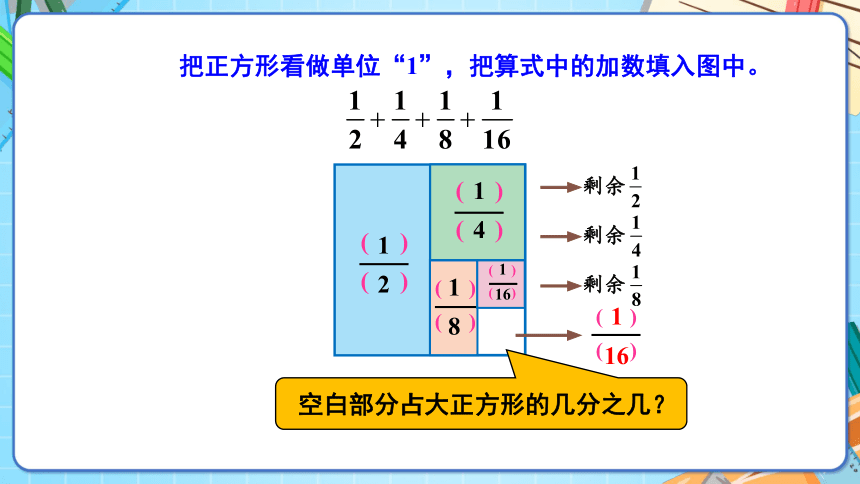
画图,想一想:
1.怎样用涂色部分表示4个加数?
2.能不能在图上用涂色的方法来表示
结果呢?
把正方形看做单位“1”,把算式中的加数填入图中。
( )
( )
1
2
剩余
( )
( )
1
4
( )
( )
1
8
剩余
剩余
( )
( )
( )
( )
1
16
空白部分占大正方形的几分之几?
1
16
( )
( )
1
2
( )
( )
1
4
( )
( )
1
8
( )
( )
1
16
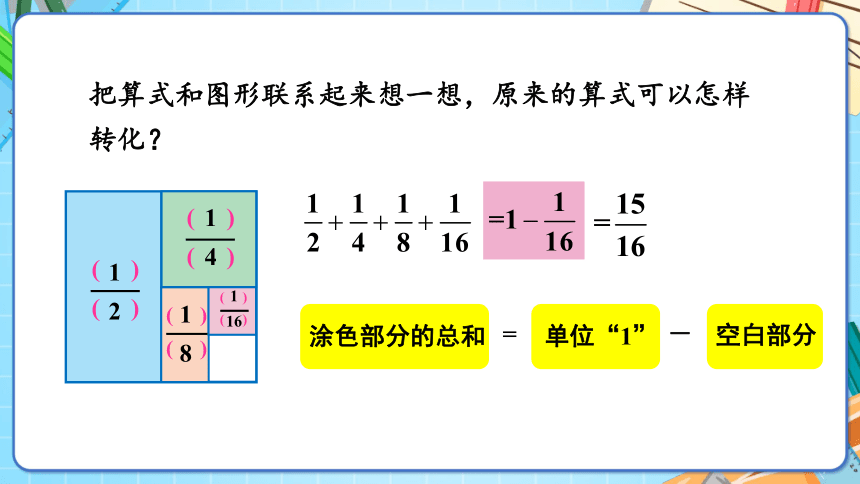
把算式和图形联系起来想一想,原来的算式可以怎样转化?
涂色部分的总和
=
单位“1”
-
空白部分
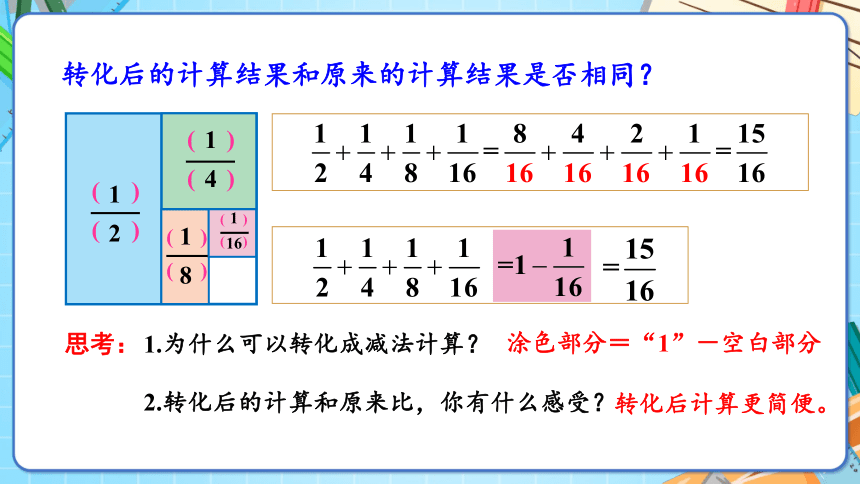
转化后的计算结果和原来的计算结果是否相同?
( )
( )
1
2
( )
( )
1
4
( )
( )
1
8
( )
( )
1
16
思考:
1.为什么可以转化成减法计算?
2.转化后的计算和原来比,你有什么感受?
涂色部分=“1”-空白部分
转化后计算更简便。
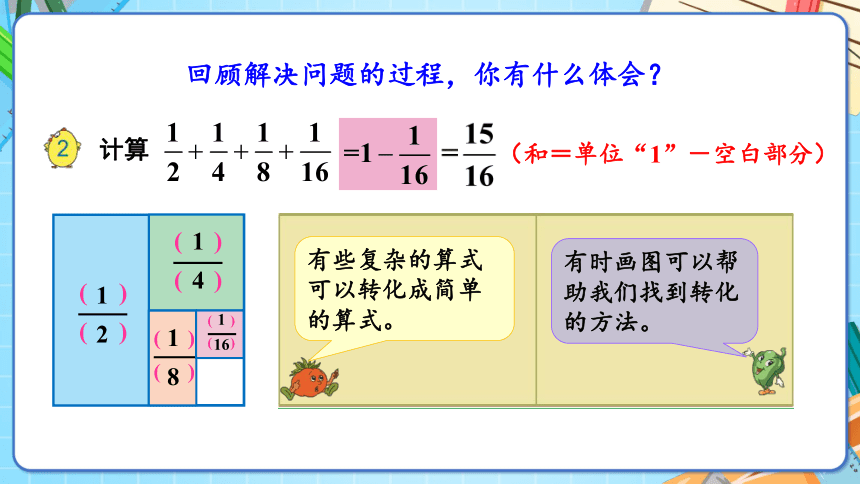
回顾解决问题的过程,你有什么体会?
计算
( )
( )
1
2
( )
( )
1
4
( )
( )
1
8
( )
( )
1
16
(和=单位“1”-空白部分)
有些复杂的算式可以转化成简单的算式。
有时画图可以帮助我们找到转化的方法。
1.计算
。
=
1-
=
( )
( )
1
2
( )
( )
1
4
( )
( )
1
8
( )
( )
1
16
【教材P108练一练第1题】
随堂练习
2.下图是一个装满了铅笔的铅笔架。你能联系梯形面积公式,计算出铅笔的只数吗?
6
7
8
9
10
11
12
13
14
15
一共装了10层,最下层有6支,最上层有15支,每相邻两层之间相差一支。
6+7+8+9+10+11+12+13+14+15
=(6+15)×10÷2
=105(支)
梯形面积=(上底+下底)×高÷2
【教材P108练一练第2题】
共10层
结合上面的计算想一想, 下面 10 个连续自然数的和, 怎样计算比较简便?
15+16+17+18+19+20+21+22+23+24
=(15+24)×10÷2
=195
=390÷2
几个连续自然数的和=(首+尾)×个数÷2
梯形面积=(上底+下底)×高÷2
15+16+17+18+19+20+21+22+23
如果少一个数,你还会求和吗?
=(15+23)×9÷2
=171
=342÷2
=38×9÷2
平均数:
171÷9=19
还有什么办法求平均数呢?
15+16+17+18+19+20+21+22+23
平均数:
(15+23)÷2=19
38
38
38
38
=19×9
=171
几个连续自然数的平均数=(首+尾)÷2
如果自然数的个数是奇数,那中间的那个数就是它的平均数。
3.计算 。
75+76+77+78+79+80+81+82+83
75+76+77+78+79+80+81+82+83
=(75+83)×9÷2
=711
=1422÷2
=79×9
=711
平均数
从不同角度计算,可以让我们计算更简便。
【教材P109练习十六第5题】
这 9 个数的平均数是多少? 你还能想到其他的简便算法吗?
4. 9999+999+99+9可以转化成怎样的算式来计算?先想一想,再算出结果。
9999+999+99+9
=(10000-1)+(1000-1)+(100-1)+(10-1)
=10000+1000+100+10-4
=11110-4
=11106
【教材P109练习十六第4题】
5. 有8支足球队参加比赛,比赛以单场淘汰制(即每场比赛淘汰1支球队,如下图)进行。一共要进行多少场比赛才能产生冠军?
每场比赛淘汰1支
球队
(冠军)
4+2+1=7(场)
换个角度思考:
要产生1个冠军,要淘汰几支球队?
8-1=7(场)
(淘汰几支就要比赛几场)
如果有16支或32支等更多的球队进行比赛,画图方便吗?怎么办?
如果有16支球队参加比赛,产生冠军要比赛多少场?
16-1=15(场)
32支球队呢?
32-1=31(场)
转化
【教材P110练习十六第6题】
7. (1)观察下面每个图形中圆的排列规律,并填空。
1
1+3=4
1+3+5=9
1+3+5+7=16
用加法求圆的个数
从1开始连续几个奇数相加
用乘法求圆的个数
1×1
2×2
3×3
4×4
=
=
=
=
奇数个数的平方
(观察算式有什么特点?)
(观察乘数和加数,你发现了什么规律?)
转化
【教材P110练习十六第7题】
7. (2)根据上面的规律用简便方法计算。
1+3+5+7+9+11
1+3+5+7+9+11+13+15+17+19
=62
=36
=102
=100
从1开始连续几个奇数相加
奇数个数的平方
转化
【教材P110练习十六第7题】
2=( )
2+4=( )
2+4+6=( )
2+4+6+8=( )
从2开始连续几个偶数相加
转化
从2开始的连续偶数相加会有怎样的规律呢?
1×2
2×3
3×4
4×5
偶数个数×(偶数个数+1)
你有什么收获?
用转化的策略求和
课堂小结
解决问题的策略(2)
苏教版五年级下册
4个分数连加,每个加数的分子都是1。
分母是有规律排列的,依次是2, 2×2,
2×2×2, 2×2×2×2。
观察这道算式, 你有什么发现?
计算 。
1
1
1
1
2×2
4×2
8×2
后一个分数总是前一个分数的 。
探究新知
计算 。
异分母分数加法
转化
同分母分数加法
计算 。
画图,想一想:
1.怎样用涂色部分表示4个加数?
2.能不能在图上用涂色的方法来表示
结果呢?
把正方形看做单位“1”,把算式中的加数填入图中。
( )
( )
1
2
剩余
( )
( )
1
4
( )
( )
1
8
剩余
剩余
( )
( )
( )
( )
1
16
空白部分占大正方形的几分之几?
1
16
( )
( )
1
2
( )
( )
1
4
( )
( )
1
8
( )
( )
1
16
把算式和图形联系起来想一想,原来的算式可以怎样转化?
涂色部分的总和
=
单位“1”
-
空白部分
转化后的计算结果和原来的计算结果是否相同?
( )
( )
1
2
( )
( )
1
4
( )
( )
1
8
( )
( )
1
16
思考:
1.为什么可以转化成减法计算?
2.转化后的计算和原来比,你有什么感受?
涂色部分=“1”-空白部分
转化后计算更简便。
回顾解决问题的过程,你有什么体会?
计算
( )
( )
1
2
( )
( )
1
4
( )
( )
1
8
( )
( )
1
16
(和=单位“1”-空白部分)
有些复杂的算式可以转化成简单的算式。
有时画图可以帮助我们找到转化的方法。
1.计算
。
=
1-
=
( )
( )
1
2
( )
( )
1
4
( )
( )
1
8
( )
( )
1
16
【教材P108练一练第1题】
随堂练习
2.下图是一个装满了铅笔的铅笔架。你能联系梯形面积公式,计算出铅笔的只数吗?
6
7
8
9
10
11
12
13
14
15
一共装了10层,最下层有6支,最上层有15支,每相邻两层之间相差一支。
6+7+8+9+10+11+12+13+14+15
=(6+15)×10÷2
=105(支)
梯形面积=(上底+下底)×高÷2
【教材P108练一练第2题】
共10层
结合上面的计算想一想, 下面 10 个连续自然数的和, 怎样计算比较简便?
15+16+17+18+19+20+21+22+23+24
=(15+24)×10÷2
=195
=390÷2
几个连续自然数的和=(首+尾)×个数÷2
梯形面积=(上底+下底)×高÷2
15+16+17+18+19+20+21+22+23
如果少一个数,你还会求和吗?
=(15+23)×9÷2
=171
=342÷2
=38×9÷2
平均数:
171÷9=19
还有什么办法求平均数呢?
15+16+17+18+19+20+21+22+23
平均数:
(15+23)÷2=19
38
38
38
38
=19×9
=171
几个连续自然数的平均数=(首+尾)÷2
如果自然数的个数是奇数,那中间的那个数就是它的平均数。
3.计算 。
75+76+77+78+79+80+81+82+83
75+76+77+78+79+80+81+82+83
=(75+83)×9÷2
=711
=1422÷2
=79×9
=711
平均数
从不同角度计算,可以让我们计算更简便。
【教材P109练习十六第5题】
这 9 个数的平均数是多少? 你还能想到其他的简便算法吗?
4. 9999+999+99+9可以转化成怎样的算式来计算?先想一想,再算出结果。
9999+999+99+9
=(10000-1)+(1000-1)+(100-1)+(10-1)
=10000+1000+100+10-4
=11110-4
=11106
【教材P109练习十六第4题】
5. 有8支足球队参加比赛,比赛以单场淘汰制(即每场比赛淘汰1支球队,如下图)进行。一共要进行多少场比赛才能产生冠军?
每场比赛淘汰1支
球队
(冠军)
4+2+1=7(场)
换个角度思考:
要产生1个冠军,要淘汰几支球队?
8-1=7(场)
(淘汰几支就要比赛几场)
如果有16支或32支等更多的球队进行比赛,画图方便吗?怎么办?
如果有16支球队参加比赛,产生冠军要比赛多少场?
16-1=15(场)
32支球队呢?
32-1=31(场)
转化
【教材P110练习十六第6题】
7. (1)观察下面每个图形中圆的排列规律,并填空。
1
1+3=4
1+3+5=9
1+3+5+7=16
用加法求圆的个数
从1开始连续几个奇数相加
用乘法求圆的个数
1×1
2×2
3×3
4×4
=
=
=
=
奇数个数的平方
(观察算式有什么特点?)
(观察乘数和加数,你发现了什么规律?)
转化
【教材P110练习十六第7题】
7. (2)根据上面的规律用简便方法计算。
1+3+5+7+9+11
1+3+5+7+9+11+13+15+17+19
=62
=36
=102
=100
从1开始连续几个奇数相加
奇数个数的平方
转化
【教材P110练习十六第7题】
2=( )
2+4=( )
2+4+6=( )
2+4+6+8=( )
从2开始连续几个偶数相加
转化
从2开始的连续偶数相加会有怎样的规律呢?
1×2
2×3
3×4
4×5
偶数个数×(偶数个数+1)
你有什么收获?
用转化的策略求和
课堂小结
