二年级 上册数学人教版8.1简单的搭配 课件 (共22张PPT)
文档属性
| 名称 | 二年级 上册数学人教版8.1简单的搭配 课件 (共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-05 00:00:00 | ||
图片预览


文档简介
(共22张PPT)
第1课时 简单的排列
数学广角——搭配(一)
8
今天我们要去数学广角,需要通过这两道山门。
这两道山门都各有密码哟!
情景导入
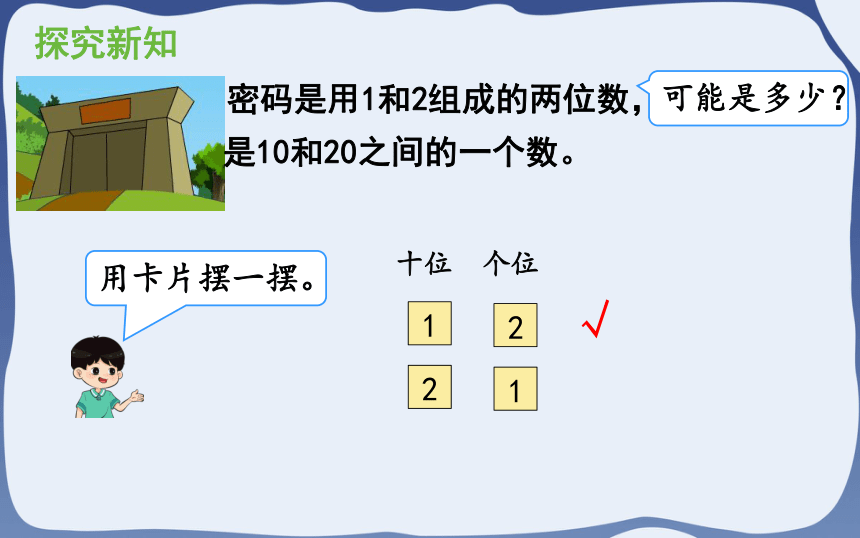
密码是用1和2组成的两位数,
1
2
1
2
十位 个位
是10和20之间的一个数。
√
用卡片摆一摆。
可能是多少?
探究新知
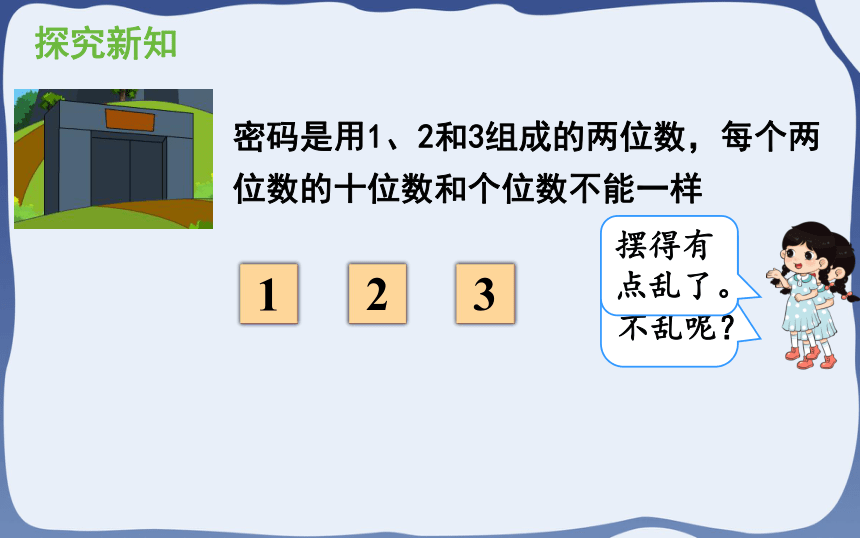
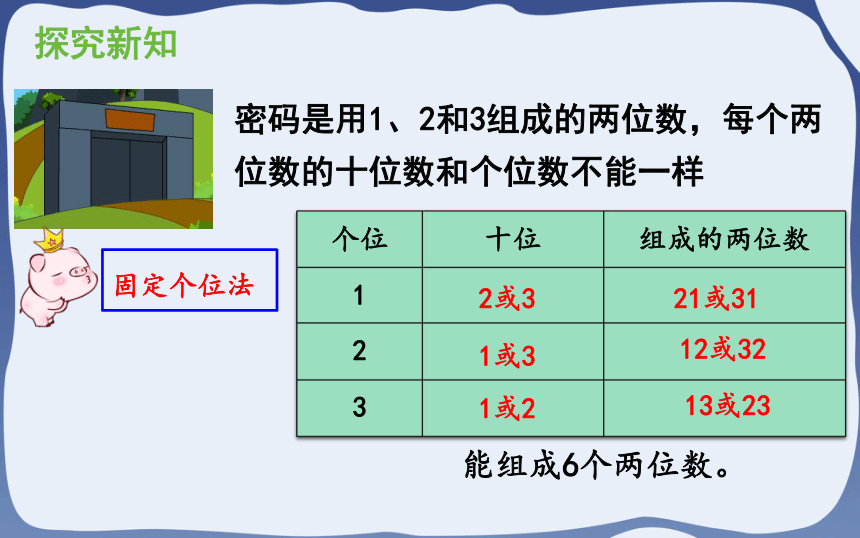
密码是用1、2和3组成的两位数,每个两位数的十位数和个位数不能一样
探究新知
1
2
3
1
1
2
2
3
3
怎样才能做到不乱呢?
摆得有点乱了。
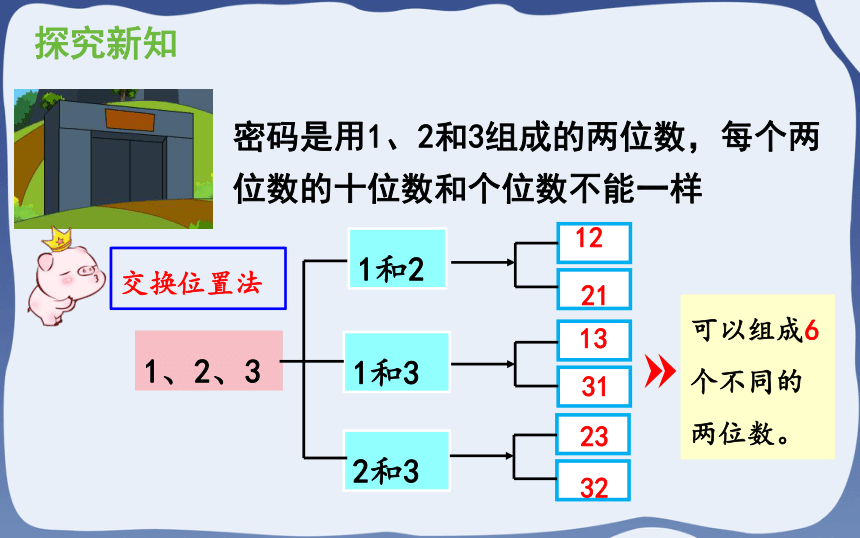
密码是用1、2和3组成的两位数,每个两位数的十位数和个位数不能一样
探究新知
可以组成6个不同的两位数。
1、2、3
1和3
2和3
1和2
12
13
21
31
32
23
交换位置法
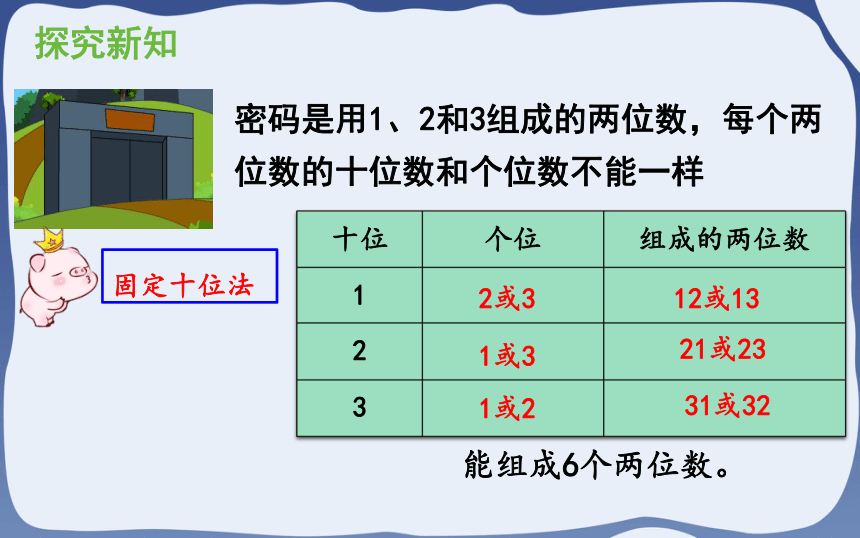
密码是用1、2和3组成的两位数,每个两位数的十位数和个位数不能一样
探究新知
十位 个位 组成的两位数
1
2
3
固定十位法
2或3
1或3
1或2
12或13
21或23
31或32
能组成6个两位数。
密码是用1、2和3组成的两位数,每个两位数的十位数和个位数不能一样
探究新知
个位 十位 组成的两位数
1
2
3
固定个位法
2或3
1或3
1或2
21或31
12或32
13或23
能组成6个两位数。
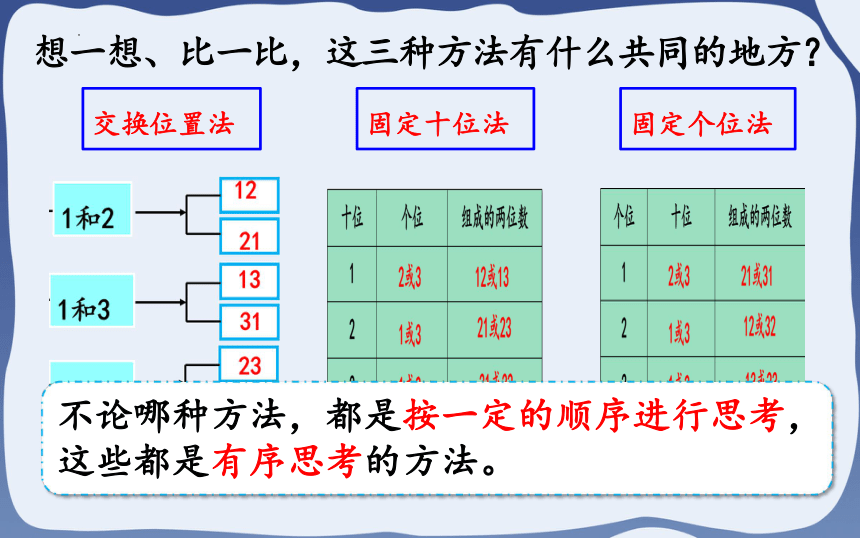
交换位置法
固定十位法
固定个位法
想一想、比一比,这三种方法有什么共同的地方?
不论哪种方法,都是按一定的顺序进行思考,这些都是有序思考的方法。
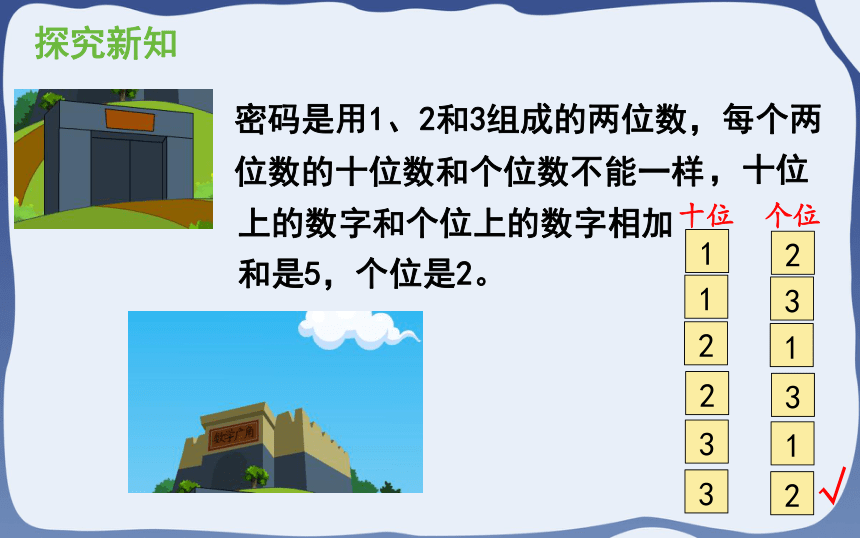
密码是用1、2和3组成的两位数,每个两位数的十位数和个位数不能一样
探究新知
上的数字和个位上的数字相加
和是5,个位是2。
,十位
十位 个位
√
1
2
3
1
1
2
3
2
1
3
2
3
1. 2名同学坐成一排合影,有多少种坐法?
① ②
① ②
答:2名同学坐成一排合影,有2种坐法。
巩固提升
答:3名同学坐成一排合影,有6种坐法。
1. 3名同学坐成一排合影,有多少种坐法?
① ② ③
① ③ ②
② ③ ①
③ ② ①
① ② ③
② ① ③
③ ① ②
巩固提升
2.用数字1、2、0组成两位数,每个两位数的十位数和个位数不能一样,能组成几个两位数?
十位 个位
1
2
2
1
1
0
2
0
0不能放在最高位。
能组成4个两位数。
答:一共有6种涂色方法。
从 、 和 3种颜色中选出2种颜色,给地图上的2个城区凃上不同的颜色,一共有多少种涂色方法?
1.从下面的3张数字卡片中,任意选出两张,能组成( )个不同的两位数,最大的两位数比最小的两位数大( )。
十位 个位
82-20=62
4
2
0
8
2
0
2
8
8
0
8
2
62
2.刘丽家的电话号码是6 3 2 0 ×××,最后三个数字是由2、4、5组成的,猜一猜,刘丽家的电话号码可能是多少呢?
刘丽家的电话号码最后三个数字可能是:
2、4、5
2、5、4
4、2、5
4、5、2
5、2、4
5、4、2
3.杨洋家的保险箱密码是由数字卡片4、6和8组成的数,他家的保险箱密码是多少?
杨洋家的保险箱密码可能是:
4、6、8
4、8、6
6、4、8
6、8、4
8、6、4
8、4、6
巧识妙记
数字排列很简单,
两个数字排列时。
交换位置就可以;
三个数字排列时,
每个数作十位,
其余数依次组,
十位数字0除外,
一定牢记在心里。
同学们,这节课你有什么收获?
课堂小结
(1)交换位置法
将这三个数字搭配成3组,然后交换个位和十位上的数字进行组合。
简单的排列问题
三个不同的数字组成不同的两位数时
1、2、3
12 21;13 31;23 32
(2)固定法
让每个数字(0除外)先作十(个)位数,然后其余两个数字依次和它组合。
简单的排列问题
三个不同的数字组成不同的两位数时
1、2、3
12 13;21 23;31 32
简单的排列问题
注:
三个不同的数字组成不同的两位数时,要想既不重复也不遗漏,就要按照一定的顺序进行。
再 见
第1课时 简单的排列
数学广角——搭配(一)
8
今天我们要去数学广角,需要通过这两道山门。
这两道山门都各有密码哟!
情景导入
密码是用1和2组成的两位数,
1
2
1
2
十位 个位
是10和20之间的一个数。
√
用卡片摆一摆。
可能是多少?
探究新知
密码是用1、2和3组成的两位数,每个两位数的十位数和个位数不能一样
探究新知
1
2
3
1
1
2
2
3
3
怎样才能做到不乱呢?
摆得有点乱了。
密码是用1、2和3组成的两位数,每个两位数的十位数和个位数不能一样
探究新知
可以组成6个不同的两位数。
1、2、3
1和3
2和3
1和2
12
13
21
31
32
23
交换位置法
密码是用1、2和3组成的两位数,每个两位数的十位数和个位数不能一样
探究新知
十位 个位 组成的两位数
1
2
3
固定十位法
2或3
1或3
1或2
12或13
21或23
31或32
能组成6个两位数。
密码是用1、2和3组成的两位数,每个两位数的十位数和个位数不能一样
探究新知
个位 十位 组成的两位数
1
2
3
固定个位法
2或3
1或3
1或2
21或31
12或32
13或23
能组成6个两位数。
交换位置法
固定十位法
固定个位法
想一想、比一比,这三种方法有什么共同的地方?
不论哪种方法,都是按一定的顺序进行思考,这些都是有序思考的方法。
密码是用1、2和3组成的两位数,每个两位数的十位数和个位数不能一样
探究新知
上的数字和个位上的数字相加
和是5,个位是2。
,十位
十位 个位
√
1
2
3
1
1
2
3
2
1
3
2
3
1. 2名同学坐成一排合影,有多少种坐法?
① ②
① ②
答:2名同学坐成一排合影,有2种坐法。
巩固提升
答:3名同学坐成一排合影,有6种坐法。
1. 3名同学坐成一排合影,有多少种坐法?
① ② ③
① ③ ②
② ③ ①
③ ② ①
① ② ③
② ① ③
③ ① ②
巩固提升
2.用数字1、2、0组成两位数,每个两位数的十位数和个位数不能一样,能组成几个两位数?
十位 个位
1
2
2
1
1
0
2
0
0不能放在最高位。
能组成4个两位数。
答:一共有6种涂色方法。
从 、 和 3种颜色中选出2种颜色,给地图上的2个城区凃上不同的颜色,一共有多少种涂色方法?
1.从下面的3张数字卡片中,任意选出两张,能组成( )个不同的两位数,最大的两位数比最小的两位数大( )。
十位 个位
82-20=62
4
2
0
8
2
0
2
8
8
0
8
2
62
2.刘丽家的电话号码是6 3 2 0 ×××,最后三个数字是由2、4、5组成的,猜一猜,刘丽家的电话号码可能是多少呢?
刘丽家的电话号码最后三个数字可能是:
2、4、5
2、5、4
4、2、5
4、5、2
5、2、4
5、4、2
3.杨洋家的保险箱密码是由数字卡片4、6和8组成的数,他家的保险箱密码是多少?
杨洋家的保险箱密码可能是:
4、6、8
4、8、6
6、4、8
6、8、4
8、6、4
8、4、6
巧识妙记
数字排列很简单,
两个数字排列时。
交换位置就可以;
三个数字排列时,
每个数作十位,
其余数依次组,
十位数字0除外,
一定牢记在心里。
同学们,这节课你有什么收获?
课堂小结
(1)交换位置法
将这三个数字搭配成3组,然后交换个位和十位上的数字进行组合。
简单的排列问题
三个不同的数字组成不同的两位数时
1、2、3
12 21;13 31;23 32
(2)固定法
让每个数字(0除外)先作十(个)位数,然后其余两个数字依次和它组合。
简单的排列问题
三个不同的数字组成不同的两位数时
1、2、3
12 13;21 23;31 32
简单的排列问题
注:
三个不同的数字组成不同的两位数时,要想既不重复也不遗漏,就要按照一定的顺序进行。
再 见
