高中数学(苏教版2019)必修第一册第7章单元综合测试B(含答案)
文档属性
| 名称 | 高中数学(苏教版2019)必修第一册第7章单元综合测试B(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 926.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-05 08:52:49 | ||
图片预览




文档简介
一、单选题
1.函数的最小正周期为,点是图象上一个最高点,将函数的图象向左平移个单位,得到函数的图象,则在区间上的值域为( )
A. B.
C. D.
2.已知函数(且)的图像经过定点,且点在角的终边上,则( )
A. B.0 C.7 D.
3.黑洞原指非常奇怪的天体,它体积小,密度大,吸引力强,任何物体到了它那里都别想再出来,数字中也有类似的“黑洞”,任意取一个数字串,长度不限,依次写出该数字串中偶数的个数、奇数的个数以及总的数字个数,把这三个数从左到右写成一个新数字串;重复以上工作,最后会得到一个反复出现的数字,我们称它为“数字黑洞”,如果把这个数字设为a,则( )
A. B. C. D.
4.已知锐角终边上一点A的坐标为,则角的弧度数为( )
A. B. C. D.
5.记函数的最小正周期为T.若,且的图象关于点中心对称,则( )
A.1 B. C. D.3
6.在地球公转过程中,太阳直射点的纬度随时间周而复始不断变化,太阳直射点回归运动的一个周期就是一个回归年.某科研小组以某年春分(太阳直射赤道且随后太阳直射点逐渐北移的时间)为初始时间,统计了连续400天太阳直射点的纬度值(太阳直射北半球时取正值,直射南半球时取负值).设第天时太阳直射点的纬度值为,该科研小组通过对数据的整理和分析.得到与近似满足.则每1200年中,要使这1200年与1200个回归年所含的天数最为接近.应设定闰年的个数为( )(精确到1)参考数据
A.290 B.291 C.292 D.293
7.阻尼器是一种以提供运动的阻力,从而达到减振效果的专业工程装置.深圳第一高楼平安金融中心的阻尼器减震装置,是亚洲最大的阻尼器,被称为“镇楼神器”.由物理学知识可知,某阻尼器模型的运动过程可近似为单摆运动,其离开平衡位置的位移s(cm)和时间t(s)的函数关系式为,其中,若该阻尼器模型在摆动过程中连续三次位移为的时间分别为,,,且,则( )
A. B.π C. D.2π
8.若函数的图象向右平移个长度单位后关于点对称,则在上的最小值为( )
A.1 B. C. D.
二、多选题
9.给出下列四个选项中,其中正确的选项有( )
A.若角的终边过点且,则
B.若是第二象限角,则为第二象限或第四象限角
C.若在单调递减,则
D.设角为锐角(单位为弧度),则
10.已知θ是锐角,那么下列各值中,sinθ+cosθ不能取得的值是( )
A. B. C. D.
11.已知函数,则( )
A.的图象可由的图象向右平移个单位长度得到
B.在上单调递增
C.在内有2个零点
D.在上的最大值为
12.已知函数的部分图象如图所示,则下列说法正确的是( )
A.
B.函数f(x)在上单调递减
C.函数g(x)=cos2x的图象可由函数f(x)的图象向左平移个单位得到
D.函数f(x)的图象关于(,0)中心对称
三、填空题
13.已知对任意都有,则等于________.
14.已知函数,将的图象上所有点横坐标变为原来的倍(纵坐标不变),再将所得函数图象向左平移个单位长度,得到图象,若在有个不同的解,则__________.
15.已知函数在上单调递增,则的取值范围为_________.
16.中国折叠扇有着深厚的文化底蕴.如图(2),在半圆(半径为20cm)中作出两个扇形和,用扇环形(图中阴影部分)制作折叠扇的扇面.记扇环形的面积为,扇形的面积为,当时,扇形的现状较为美观,则此时扇形的半径为__________cm
四、解答题
17.已知函数周期是.
(1)求的解析式,并求的单调递增区间;
(2)将图像上所有点的横坐标扩大到原来的2倍,再向左平移个单位,最后将整个函数图像向上平移个单位后得到函数的图像,若时,恒成立,求m得取值范围.
18.m=cos+ cos+ cos+ cos+ cos
(1)化简m=
(2)若 f(cos(x))=16x 求 f(m)+m=?
(3)若g((sinx))=16x+cosx,求g(cos)的值
19.已知函数.
(1)求它的定义域和值域;
(2)求它的单调区间;
(3)判断它的奇偶性;
(4)判断它的周期性,如果是周期函数,求出它的最小正周期.
20.如图,某地有三家工厂,分别位于矩形的两个顶点A、及的中点 处.km,km.为了处理这三家工厂的污水,现要在该矩形区域内(含边界)且与A、等距的一点处,建造一个污水处理厂,并铺设三条排污管道,,.记铺设管道的总长度为ykm.
(1)设(弧度),将表示成的函数并求函数的定义域;
(2)假设铺设的污水管道总长度是km,请确定污水处理厂的位置.
21.已知:,:.
(1)当时,求实数的取值范围;
(2)若是的充分不必要条件,求实数的取值范围.
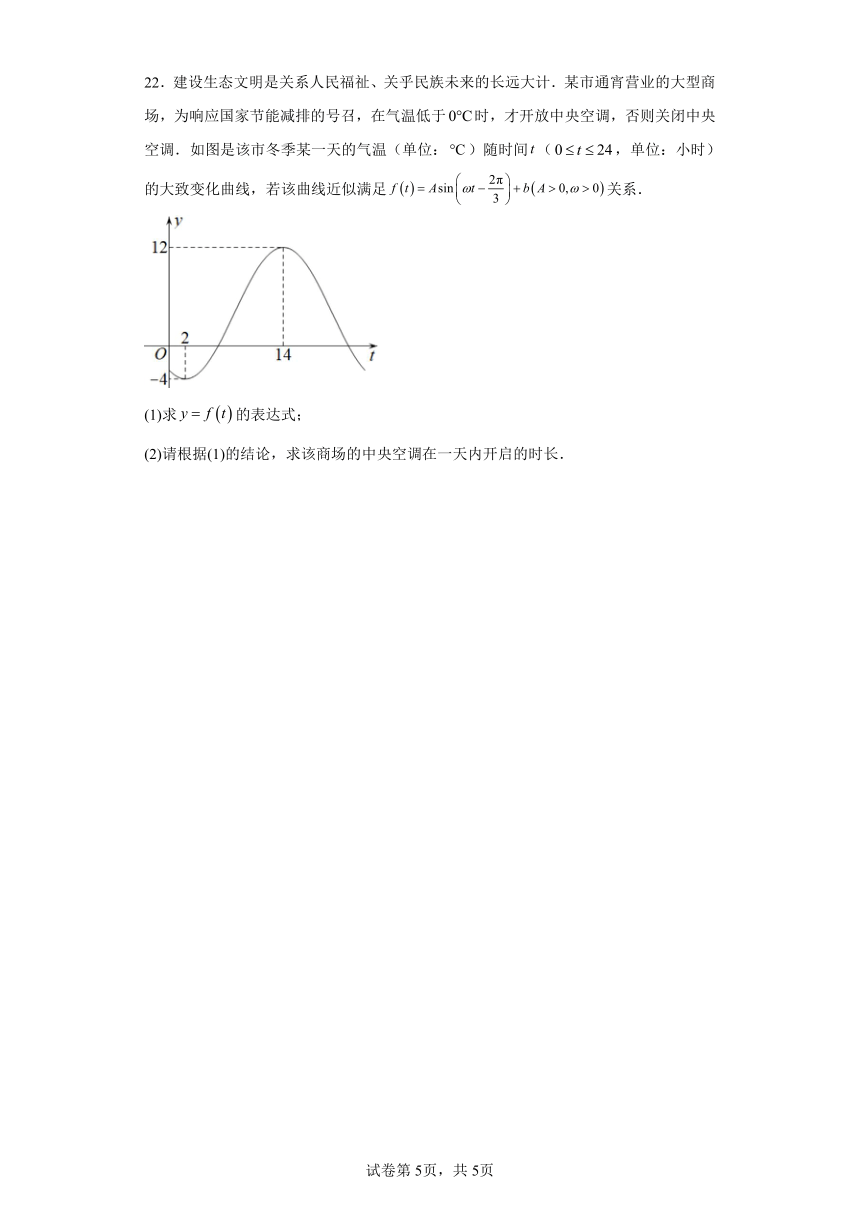
22.建设生态文明是关系人民福祉、关乎民族未来的长远大计.某市通宵营业的大型商场,为响应国家节能减排的号召,在气温低于时,才开放中央空调,否则关闭中央空调.如图是该市冬季某一天的气温(单位:)随时间(,单位:小时)的大致变化曲线,若该曲线近似满足关系.
(1)求的表达式;
(2)请根据(1)的结论,求该商场的中央空调在一天内开启的时长.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】由最小正周期求出,点是图象上一个最高点求得 A、,利用平移规律得到,
根据的范围得到的单调性,利用单调性可得答案.
【详解】因为函数的最小正周期为,所以,,
因为点是图象上一个最高点,所以A=2,,又,所以,
所以,,
当时,,
因为在区间上单调递增,在区间上单调递减,
又,,,所以在区间上的值域为.
故选:A.
2.D
【分析】由题知,进而根据三角函数定义结合齐次式求解即可.
【详解】解:令得,故定点为,
所以由三角函数定义得,
所以
故选:D
3.D
【分析】根据题意可得数字黑洞为123,然后利用诱导公式即得.
【详解】根据“数字黑洞”的定义,任取数字2021,经过一步之后为314,经过第二步之后为123,再变为123,再变为123,
所以数字黑洞为123,即,
∴.
故选:D.
4.A
【分析】先根据定义得正切值,再根据诱导公式求解
【详解】,
又,为锐角,
∴ ,
故选:A.
5.A
【分析】由三角函数的图象与性质可求得参数,进而可得函数解析式,代入即可得解.
【详解】由函数的最小正周期T满足,得,解得,
又因为函数图象关于点对称,所以,且,
所以,所以,,
所以.
故选:A
6.B
【分析】设闰年个数为,根据闰年个数对应天数一致的原则建立关系式,求解即可.
【详解】解:,
所以一个回归年对应的天数为天
假设1200年中,设定闰年的个数为,则平年有个,
所以
解得:.
故选:B.
7.B
【分析】利用正弦型函数的性质画出函数图象,并确定连续三次位移为的时间,,,即可得,可求参数.
【详解】由正弦型函数的性质,函数示意图如下:
所以,则,可得.
故选:B
8.C
【分析】由图像平移过程写出平移后的解析式,利用正弦函数的对称性求参数,最后由正弦型函数的单调性求区间最小值即可.
【详解】将向右平移个长度单位后,得到,
∵关于对称,
∴,
∴,即,
又,则,即,
由知:,则,
∴在上的最小值为.
故选:C.
9.AD
【分析】A由终边上的点可得即可求m值;B由题设,进而求的范围即可知所在的象限;C利用对数复合函数的单调性,结合单调区间求参数范围;D利用单位圆确定所代表的长度,即可比较大小.
【详解】A:,易知且,则,正确;
B:,则,可知为第一象限或第三象限角,错误;
C:由,当时,上递增,上递减;当时,上递减,上递增;而在上递减,则且,可得,故错误;
D:如下图,单位圆中,显然,正确;
故选:AD
10.BCD
【分析】由题意利用辅助角公式化简,再利用正弦函数的定义域和值域,求得它的范围,从而得出结论.
【详解】解:,,
又,
,
.
选项A在此范围,其余选项都不在此范围,
故选:BCD.
11.BC
【分析】A.根据函数的平移判断;B.求出函数的单调增区间来判断;C.求出函数的零点来判断;D.求出函数的最大值来判断;
【详解】由题得,
由的图象向右平移个单位长度,得到的图象,所以选项A错误;
令,
得其增区间为,
所以在上单调递增,所以选项B正确;
令得,
得,又.
所以可取,即有2个零点,所以选项正确;
由得,
所以,所以选项D错误.
故选:BC.
12.AC
【分析】首先利用“五点法”求函数的解析式,利用函数的性质求函数的单调递减区间,判断选项,再利用平移规律,判断选项,利用对称中心公式求函数的对称中心,判断选项.
【详解】解:对于A:根据函数的图象:φ=(k∈Z),解得φ=(k∈Z),
由于|φ|<,
所以当k=0时,φ=.
由于f(0)=,所以A,解得A=.
所以f(x)=,故A正确;
对于B:令(k∈Z),
解得:(k∈Z),
所以函数的单调递减区间为[](k∈Z),
故函数在[]上单调递减,在[]上单调递增,故B错误;
对于C:函数f(x+)=,故C正确;
对于D:令(k∈Z),解得(k∈Z),
所以函数的对称中心为()(k∈Z),由于k为整数,故D错误;
故选:AC.
【点睛】思路点睛:本题考查的解析式和性质的判断,可以整体代入验证的方法判断函数性质:(1)对于函数,其对称轴一定经过图象的最高点或最低点,对称中心的横坐标一定是函数的零点,因此判断直线或点是否是函数的对称轴和对称中心时,可通过验证的值进行判断;(2)判断某区间是否是函数的单调区间时,也可以求的范围,验证此区间是否是函数的增或减区间.
13.
【分析】由给定等式可得图象的一条对称轴,再借助正弦型函数的性质即可得解.
【详解】因对任意都有,则直线是图象的一条对称轴,
所以.
故答案为:
14.
【分析】根据三角函数平移伸缩变换法则求出函数的解析式,再利用函数的对称性即可求出在的解,即可得解.
【详解】根据题意可知,,由得,由,可得,所以函数关于对称,因为,所以由可得,因此.
故答案为:.
15.
【分析】由含绝对值正弦函数的区间单调性,结合正弦型函数的性质求的范围.
【详解】当时,.
因为,所以,.
因为函数在上单调递增,
所以,解得.
故答案为:
16.
【分析】根据已知条件和扇形的面积公式可求得答案.
【详解】设,半圆O的半径为r,扇形OCD的半径为,
,所以,即,
所以,所以,又,所以,
故答案为:.
17.(1),单调递增区间为,;(2).
【解析】(1)根据正弦和余弦的二倍角公式化简可得,由,解得,带入正弦函数的递增区间,化简即可得解;
(2)根据三角函数的平移和伸缩变换可得,根据题意只需要,分别在范围内求出的最值即可得解.
【详解】(1)
由,解得
所以,
∵
∴
∴
∴的单调递增区间为,
(2)依题意得
因为,所以
因为当时,恒成立
所以只需转化为求的最大值与最小值
当时,为单调减函数
所以,,
从而,,即
所以m的取值范围是.
【点睛】本题考查了三角函数的单调性和最值,考查了三角函数的辅助角公式和平移伸缩变换,有一定的计算量,属于中档题.本题关键点有:
(1)三角函数基本量的理解应用;
(2)三角函数图像平移伸缩变换的方法;
(3)恒成立思想的理解及转化.
18.(1);(2)或(3)或,.
【分析】(1)利用诱导公式化简即得解;
(2)求出或,,即得解;
(3)求出或,,即得解.
【详解】(1)m= ,
所以m=;
(2)或
所以或,
所以或
(3)或,.
所以或,.
所以或,.
19.(1)定义域为,值域为;(2)单调增区间为,单调减区间为;(3)非奇非偶函数; (4).
【分析】(1)利用两角和差的三角函数,结合对数的运算化简可得,
由真数大于零,即,利用三角函数的图象和性质求解,即得函数的定义域;根据三角函数的值域和对数函数的图象与性质,可求得函数的值域;
(2)利用对数函数的单调性,三角函数的单调性,结合复合函数的单调性可求得函数的单调增减区间;
(3)利用奇偶函数的定义域的对称性,结合(1)中所的定义域,即可得到函数为非奇非偶函数;
(4)根据三角函数的周期性,即可得到函数的周期.
【详解】(1),
由,解得
∴函数的定义域为;
由,∴,∴函数的值域为;
(2)在定义域内,当,即时,是单调递增的,故函数时单调递减的;
当,即时,是单调递减的,故函数时单调递增的;
∴单调增区间为,单调减区间为;
(3)由(1)得函数的定义域为,
定义域不关于原点对称,故函数为非奇非偶函数;
(4)∵的最小正周期为,∴函数的最小正周期为.
【点睛】本题考查对数函数与三角函数的复合函数的定义域,值域,单调性,奇偶性和周期性问题,关键是掌握复合函数的单调性求解方法,熟练掌握三角函数的单调性,简单三角不等式的求解方法,并注意单调性求解和奇偶性判定时一定要考察清楚函数的定义域.
20.(1)
(2)位置是在线段的中垂线上且离的距离是 km
【分析】(1)依据题给条件,先分别求得的表达式,进而得到管道总长度y的表达式,再去求其定义域即可解决;
(2)先解方程,求得,再去确定污水处理厂的位置.
【详解】(1)矩形中,km,km,
,,
则,
则
(2)令
则
又,即,则,则
此时
所以确定污水处理厂的位置是在线段的中垂线上且离的距离是 km
21.(1);(2).
【分析】(1)将代入即可求解;(2)首先结合已知条件分别求出命题和的解,写出,然后利用充分不必要的特征即可求解.
【详解】(1)由题意可知,,解得,
故实数的取值范围为;
(2)由,解得或,
由,解得,
故命题:或;命题:,
从而:或,
因为是的充分不必要条件,
所以或或,
从而,解得,
故实数的取值范围为.
22.(1) ,;(2) 8小时.
【分析】(1)根据三角函数的图像即可求的表达式;
(2)根据正弦函数的图像与性质解,结合即可求解.
【详解】解:(1)因为图像上最低点坐标为,与之相邻的最高点坐标为,
所以,,,
所以,解得.
所以,.
(2)由(1)得,,
所以,
所以,
解得,
因为,
所以,.
所以该商场的中央空调应在本天内开启时长为8小时.
答案第1页,共2页
答案第1页,共2页
1.函数的最小正周期为,点是图象上一个最高点,将函数的图象向左平移个单位,得到函数的图象,则在区间上的值域为( )
A. B.
C. D.
2.已知函数(且)的图像经过定点,且点在角的终边上,则( )
A. B.0 C.7 D.
3.黑洞原指非常奇怪的天体,它体积小,密度大,吸引力强,任何物体到了它那里都别想再出来,数字中也有类似的“黑洞”,任意取一个数字串,长度不限,依次写出该数字串中偶数的个数、奇数的个数以及总的数字个数,把这三个数从左到右写成一个新数字串;重复以上工作,最后会得到一个反复出现的数字,我们称它为“数字黑洞”,如果把这个数字设为a,则( )
A. B. C. D.
4.已知锐角终边上一点A的坐标为,则角的弧度数为( )
A. B. C. D.
5.记函数的最小正周期为T.若,且的图象关于点中心对称,则( )
A.1 B. C. D.3
6.在地球公转过程中,太阳直射点的纬度随时间周而复始不断变化,太阳直射点回归运动的一个周期就是一个回归年.某科研小组以某年春分(太阳直射赤道且随后太阳直射点逐渐北移的时间)为初始时间,统计了连续400天太阳直射点的纬度值(太阳直射北半球时取正值,直射南半球时取负值).设第天时太阳直射点的纬度值为,该科研小组通过对数据的整理和分析.得到与近似满足.则每1200年中,要使这1200年与1200个回归年所含的天数最为接近.应设定闰年的个数为( )(精确到1)参考数据
A.290 B.291 C.292 D.293
7.阻尼器是一种以提供运动的阻力,从而达到减振效果的专业工程装置.深圳第一高楼平安金融中心的阻尼器减震装置,是亚洲最大的阻尼器,被称为“镇楼神器”.由物理学知识可知,某阻尼器模型的运动过程可近似为单摆运动,其离开平衡位置的位移s(cm)和时间t(s)的函数关系式为,其中,若该阻尼器模型在摆动过程中连续三次位移为的时间分别为,,,且,则( )
A. B.π C. D.2π
8.若函数的图象向右平移个长度单位后关于点对称,则在上的最小值为( )
A.1 B. C. D.
二、多选题
9.给出下列四个选项中,其中正确的选项有( )
A.若角的终边过点且,则
B.若是第二象限角,则为第二象限或第四象限角
C.若在单调递减,则
D.设角为锐角(单位为弧度),则
10.已知θ是锐角,那么下列各值中,sinθ+cosθ不能取得的值是( )
A. B. C. D.
11.已知函数,则( )
A.的图象可由的图象向右平移个单位长度得到
B.在上单调递增
C.在内有2个零点
D.在上的最大值为
12.已知函数的部分图象如图所示,则下列说法正确的是( )
A.
B.函数f(x)在上单调递减
C.函数g(x)=cos2x的图象可由函数f(x)的图象向左平移个单位得到
D.函数f(x)的图象关于(,0)中心对称
三、填空题
13.已知对任意都有,则等于________.
14.已知函数,将的图象上所有点横坐标变为原来的倍(纵坐标不变),再将所得函数图象向左平移个单位长度,得到图象,若在有个不同的解,则__________.
15.已知函数在上单调递增,则的取值范围为_________.
16.中国折叠扇有着深厚的文化底蕴.如图(2),在半圆(半径为20cm)中作出两个扇形和,用扇环形(图中阴影部分)制作折叠扇的扇面.记扇环形的面积为,扇形的面积为,当时,扇形的现状较为美观,则此时扇形的半径为__________cm
四、解答题
17.已知函数周期是.
(1)求的解析式,并求的单调递增区间;
(2)将图像上所有点的横坐标扩大到原来的2倍,再向左平移个单位,最后将整个函数图像向上平移个单位后得到函数的图像,若时,恒成立,求m得取值范围.
18.m=cos+ cos+ cos+ cos+ cos
(1)化简m=
(2)若 f(cos(x))=16x 求 f(m)+m=?
(3)若g((sinx))=16x+cosx,求g(cos)的值
19.已知函数.
(1)求它的定义域和值域;
(2)求它的单调区间;
(3)判断它的奇偶性;
(4)判断它的周期性,如果是周期函数,求出它的最小正周期.
20.如图,某地有三家工厂,分别位于矩形的两个顶点A、及的中点 处.km,km.为了处理这三家工厂的污水,现要在该矩形区域内(含边界)且与A、等距的一点处,建造一个污水处理厂,并铺设三条排污管道,,.记铺设管道的总长度为ykm.
(1)设(弧度),将表示成的函数并求函数的定义域;
(2)假设铺设的污水管道总长度是km,请确定污水处理厂的位置.
21.已知:,:.
(1)当时,求实数的取值范围;
(2)若是的充分不必要条件,求实数的取值范围.
22.建设生态文明是关系人民福祉、关乎民族未来的长远大计.某市通宵营业的大型商场,为响应国家节能减排的号召,在气温低于时,才开放中央空调,否则关闭中央空调.如图是该市冬季某一天的气温(单位:)随时间(,单位:小时)的大致变化曲线,若该曲线近似满足关系.
(1)求的表达式;
(2)请根据(1)的结论,求该商场的中央空调在一天内开启的时长.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】由最小正周期求出,点是图象上一个最高点求得 A、,利用平移规律得到,
根据的范围得到的单调性,利用单调性可得答案.
【详解】因为函数的最小正周期为,所以,,
因为点是图象上一个最高点,所以A=2,,又,所以,
所以,,
当时,,
因为在区间上单调递增,在区间上单调递减,
又,,,所以在区间上的值域为.
故选:A.
2.D
【分析】由题知,进而根据三角函数定义结合齐次式求解即可.
【详解】解:令得,故定点为,
所以由三角函数定义得,
所以
故选:D
3.D
【分析】根据题意可得数字黑洞为123,然后利用诱导公式即得.
【详解】根据“数字黑洞”的定义,任取数字2021,经过一步之后为314,经过第二步之后为123,再变为123,再变为123,
所以数字黑洞为123,即,
∴.
故选:D.
4.A
【分析】先根据定义得正切值,再根据诱导公式求解
【详解】,
又,为锐角,
∴ ,
故选:A.
5.A
【分析】由三角函数的图象与性质可求得参数,进而可得函数解析式,代入即可得解.
【详解】由函数的最小正周期T满足,得,解得,
又因为函数图象关于点对称,所以,且,
所以,所以,,
所以.
故选:A
6.B
【分析】设闰年个数为,根据闰年个数对应天数一致的原则建立关系式,求解即可.
【详解】解:,
所以一个回归年对应的天数为天
假设1200年中,设定闰年的个数为,则平年有个,
所以
解得:.
故选:B.
7.B
【分析】利用正弦型函数的性质画出函数图象,并确定连续三次位移为的时间,,,即可得,可求参数.
【详解】由正弦型函数的性质,函数示意图如下:
所以,则,可得.
故选:B
8.C
【分析】由图像平移过程写出平移后的解析式,利用正弦函数的对称性求参数,最后由正弦型函数的单调性求区间最小值即可.
【详解】将向右平移个长度单位后,得到,
∵关于对称,
∴,
∴,即,
又,则,即,
由知:,则,
∴在上的最小值为.
故选:C.
9.AD
【分析】A由终边上的点可得即可求m值;B由题设,进而求的范围即可知所在的象限;C利用对数复合函数的单调性,结合单调区间求参数范围;D利用单位圆确定所代表的长度,即可比较大小.
【详解】A:,易知且,则,正确;
B:,则,可知为第一象限或第三象限角,错误;
C:由,当时,上递增,上递减;当时,上递减,上递增;而在上递减,则且,可得,故错误;
D:如下图,单位圆中,显然,正确;
故选:AD
10.BCD
【分析】由题意利用辅助角公式化简,再利用正弦函数的定义域和值域,求得它的范围,从而得出结论.
【详解】解:,,
又,
,
.
选项A在此范围,其余选项都不在此范围,
故选:BCD.
11.BC
【分析】A.根据函数的平移判断;B.求出函数的单调增区间来判断;C.求出函数的零点来判断;D.求出函数的最大值来判断;
【详解】由题得,
由的图象向右平移个单位长度,得到的图象,所以选项A错误;
令,
得其增区间为,
所以在上单调递增,所以选项B正确;
令得,
得,又.
所以可取,即有2个零点,所以选项正确;
由得,
所以,所以选项D错误.
故选:BC.
12.AC
【分析】首先利用“五点法”求函数的解析式,利用函数的性质求函数的单调递减区间,判断选项,再利用平移规律,判断选项,利用对称中心公式求函数的对称中心,判断选项.
【详解】解:对于A:根据函数的图象:φ=(k∈Z),解得φ=(k∈Z),
由于|φ|<,
所以当k=0时,φ=.
由于f(0)=,所以A,解得A=.
所以f(x)=,故A正确;
对于B:令(k∈Z),
解得:(k∈Z),
所以函数的单调递减区间为[](k∈Z),
故函数在[]上单调递减,在[]上单调递增,故B错误;
对于C:函数f(x+)=,故C正确;
对于D:令(k∈Z),解得(k∈Z),
所以函数的对称中心为()(k∈Z),由于k为整数,故D错误;
故选:AC.
【点睛】思路点睛:本题考查的解析式和性质的判断,可以整体代入验证的方法判断函数性质:(1)对于函数,其对称轴一定经过图象的最高点或最低点,对称中心的横坐标一定是函数的零点,因此判断直线或点是否是函数的对称轴和对称中心时,可通过验证的值进行判断;(2)判断某区间是否是函数的单调区间时,也可以求的范围,验证此区间是否是函数的增或减区间.
13.
【分析】由给定等式可得图象的一条对称轴,再借助正弦型函数的性质即可得解.
【详解】因对任意都有,则直线是图象的一条对称轴,
所以.
故答案为:
14.
【分析】根据三角函数平移伸缩变换法则求出函数的解析式,再利用函数的对称性即可求出在的解,即可得解.
【详解】根据题意可知,,由得,由,可得,所以函数关于对称,因为,所以由可得,因此.
故答案为:.
15.
【分析】由含绝对值正弦函数的区间单调性,结合正弦型函数的性质求的范围.
【详解】当时,.
因为,所以,.
因为函数在上单调递增,
所以,解得.
故答案为:
16.
【分析】根据已知条件和扇形的面积公式可求得答案.
【详解】设,半圆O的半径为r,扇形OCD的半径为,
,所以,即,
所以,所以,又,所以,
故答案为:.
17.(1),单调递增区间为,;(2).
【解析】(1)根据正弦和余弦的二倍角公式化简可得,由,解得,带入正弦函数的递增区间,化简即可得解;
(2)根据三角函数的平移和伸缩变换可得,根据题意只需要,分别在范围内求出的最值即可得解.
【详解】(1)
由,解得
所以,
∵
∴
∴
∴的单调递增区间为,
(2)依题意得
因为,所以
因为当时,恒成立
所以只需转化为求的最大值与最小值
当时,为单调减函数
所以,,
从而,,即
所以m的取值范围是.
【点睛】本题考查了三角函数的单调性和最值,考查了三角函数的辅助角公式和平移伸缩变换,有一定的计算量,属于中档题.本题关键点有:
(1)三角函数基本量的理解应用;
(2)三角函数图像平移伸缩变换的方法;
(3)恒成立思想的理解及转化.
18.(1);(2)或(3)或,.
【分析】(1)利用诱导公式化简即得解;
(2)求出或,,即得解;
(3)求出或,,即得解.
【详解】(1)m= ,
所以m=;
(2)或
所以或,
所以或
(3)或,.
所以或,.
所以或,.
19.(1)定义域为,值域为;(2)单调增区间为,单调减区间为;(3)非奇非偶函数; (4).
【分析】(1)利用两角和差的三角函数,结合对数的运算化简可得,
由真数大于零,即,利用三角函数的图象和性质求解,即得函数的定义域;根据三角函数的值域和对数函数的图象与性质,可求得函数的值域;
(2)利用对数函数的单调性,三角函数的单调性,结合复合函数的单调性可求得函数的单调增减区间;
(3)利用奇偶函数的定义域的对称性,结合(1)中所的定义域,即可得到函数为非奇非偶函数;
(4)根据三角函数的周期性,即可得到函数的周期.
【详解】(1),
由,解得
∴函数的定义域为;
由,∴,∴函数的值域为;
(2)在定义域内,当,即时,是单调递增的,故函数时单调递减的;
当,即时,是单调递减的,故函数时单调递增的;
∴单调增区间为,单调减区间为;
(3)由(1)得函数的定义域为,
定义域不关于原点对称,故函数为非奇非偶函数;
(4)∵的最小正周期为,∴函数的最小正周期为.
【点睛】本题考查对数函数与三角函数的复合函数的定义域,值域,单调性,奇偶性和周期性问题,关键是掌握复合函数的单调性求解方法,熟练掌握三角函数的单调性,简单三角不等式的求解方法,并注意单调性求解和奇偶性判定时一定要考察清楚函数的定义域.
20.(1)
(2)位置是在线段的中垂线上且离的距离是 km
【分析】(1)依据题给条件,先分别求得的表达式,进而得到管道总长度y的表达式,再去求其定义域即可解决;
(2)先解方程,求得,再去确定污水处理厂的位置.
【详解】(1)矩形中,km,km,
,,
则,
则
(2)令
则
又,即,则,则
此时
所以确定污水处理厂的位置是在线段的中垂线上且离的距离是 km
21.(1);(2).
【分析】(1)将代入即可求解;(2)首先结合已知条件分别求出命题和的解,写出,然后利用充分不必要的特征即可求解.
【详解】(1)由题意可知,,解得,
故实数的取值范围为;
(2)由,解得或,
由,解得,
故命题:或;命题:,
从而:或,
因为是的充分不必要条件,
所以或或,
从而,解得,
故实数的取值范围为.
22.(1) ,;(2) 8小时.
【分析】(1)根据三角函数的图像即可求的表达式;
(2)根据正弦函数的图像与性质解,结合即可求解.
【详解】解:(1)因为图像上最低点坐标为,与之相邻的最高点坐标为,
所以,,,
所以,解得.
所以,.
(2)由(1)得,,
所以,
所以,
解得,
因为,
所以,.
所以该商场的中央空调应在本天内开启时长为8小时.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
