高中数学(苏教版2019)必修第二册第11章单元综合测试A(含答案)
文档属性
| 名称 | 高中数学(苏教版2019)必修第二册第11章单元综合测试A(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-05 09:55:38 | ||
图片预览



文档简介
一、单选题
1.人们通常把顶角为36°的等腰三角形称为黄金三角形,因为它的底边和腰长的比值等于黄金分割比,我们熟悉的五角星就是由5个黄金三角形和1个正五边形组成的,如图,三角形ABC就是一个黄金三角形,根据以上信息,可得=( )
A. B. C. D.
2.已知在ABC中,a=x,b=2,B=30°,若三角形有两解,则x的取值范围是( )
A.x>2 B.03.在中,角的对边分别是,,,,则( )
A. B. C.或 D.无解
4.唐代数学家、天文学家僧一行,利用“九服晷影算法”建立了从0°到80°的晷影长l与太阳天顶距θ的对应数表.已知晷影长l、表高h与太阳天顶距θ满足l=htanθ,当晷影长为0.7时,天顶距为5°.若天顶距为1°时,则晷影长为( )(参考数据:tan1°≈0.0175,tan3°≈0.0349,tan5°≈0.0875)
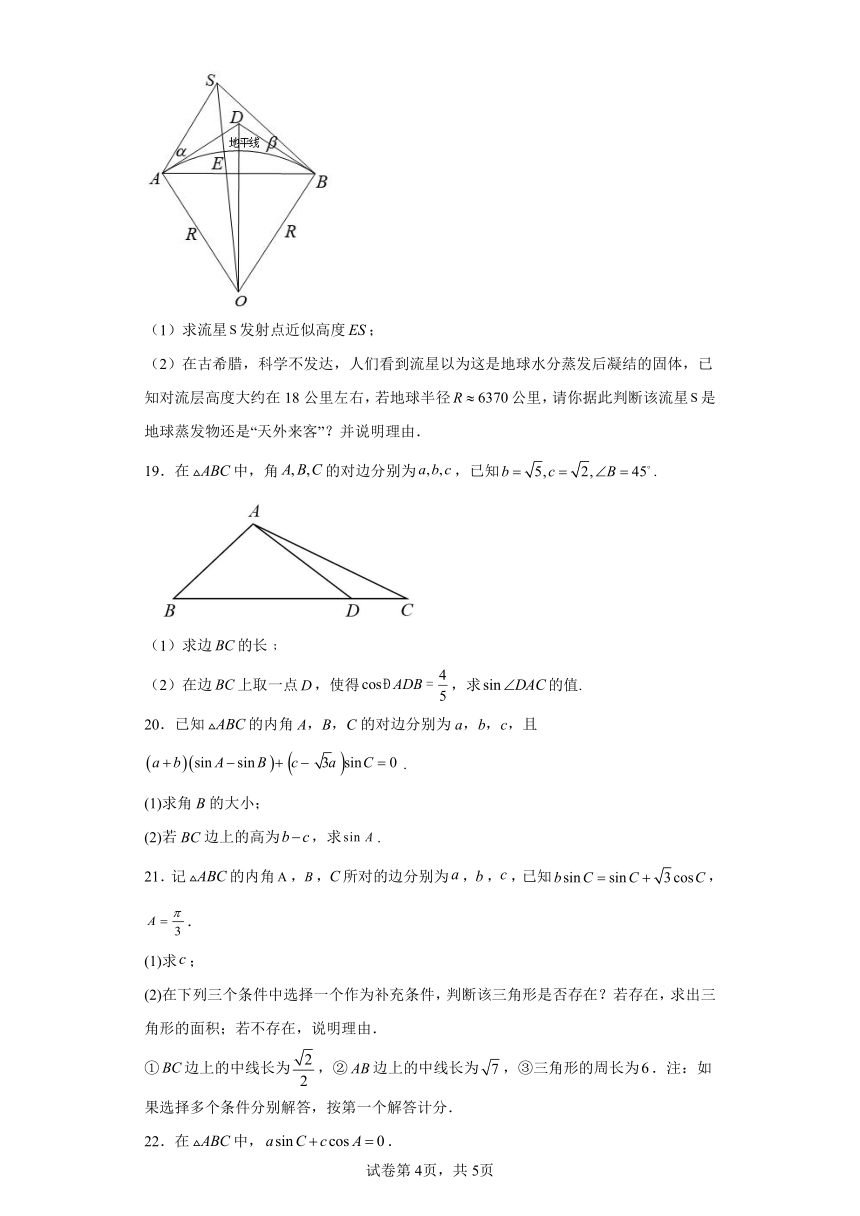
A.0.14 B.0.16 C.0.18 D.0.24
5.△ABC的内角A,B,C的对边分别为a,b,c,已知asinA-bsinB=4csinC,cosA=-,则=
A.6 B.5 C.4 D.3
6.岳阳楼与湖北武汉黄鹤楼,江西南昌滕王阁并称为“江南三大名楼”,是“中国十大历史文化名楼”之一,世称“天下第一楼”.其地处岳阳古城西门城墙之上,紧靠洞庭湖畔,下瞰洞庭,前望君山.始建于东汉建安二十年(215年),历代屡加重修,现存建筑沿袭清光绪六年(1880年)重建时的形制与格局.因北宋滕宗谅重修岳阳楼,邀好友范仲淹作《岳阳楼记》使得岳阳楼著称于世.自古有"洞庭天下水,岳阳天下楼"之美誉.小李为测量岳阳楼的高度选取了与底部水平的直线,如图,测得,,米,则岳阳楼的高度约为(,)( )
A.米 B.米 C.米 D.米
7.在中,角所对的边分别为,若,则( )
A. B.或 C. D.或
8.已知a、b、c分别为△ABC的三内角A、B、C的对边,,则( )
A. B. C. D.
二、多选题
9.已知,,分别为内角,,的对边,,且,则下列结论中正确的是( )
A. B.
C.面积的最大值为 D.面积的最大值为
10.设的内角、、所对边的长分别为、、,下列命题正确的是( )
A.若,则
B.若,则
C.若,则
D.若,则
11.已知中,角,,的对边分别为,,,且,则角的值不可能是( )
A.45° B.60° C.75° D.90°
12.下列结论正确的是( )
A.在中,若,则
B.在锐角三角形中,不等式恒成立
C.在中,若,,则为等腰直角三角形
D.在中,若,,三角形面积,则三角形外接圆半径为
三、填空题
13.在中,,,,那么的长度为______.
14.在中,内角A,B,C所对边分别为a,b,c.若的面积为,则__________.
15.在中,∠A=60°,AB=1,AC=2,则BC=___________.
16.在中,若,则的大小为__________.
四、解答题
17.在中,A,B,C的对边分别是a,b,c,且.
(1)求a的值;
(2)若,求边上的高的长.
18.仰望星空,时有流星划过天际,令我们感叹生命的短暂,又深深震撼我们凡俗的心灵.流星是什么?从古至今,人们作过无数种猜测.古希腊亚里士多德说,那是地球上的蒸发物,近代有人进一步认为,那是地球上磷火升空后的燃烧现象.10世纪波斯著名数学家、天文学家阿尔·库希设计出一种方案,通过两个观测者异地同时观察同一颗流星,来测定其发射点的高度.如图,假设地球是一个标准的球体,为地球的球心,为地平线,有两个观测者在地球上的,两地同时观测到一颗流星,观测的仰角分别为,,其中,,为了方便计算,我们考虑一种理想状态,假设两个观测者在地球上的,两点测得,,地球半径为公里,两个观测者的距离 .(参考数据:,)
(1)求流星发射点近似高度;
(2)在古希腊,科学不发达,人们看到流星以为这是地球水分蒸发后凝结的固体,已知对流层高度大约在18公里左右,若地球半径公里,请你据此判断该流星是地球蒸发物还是“天外来客”?并说明理由.
19.在中,角的对边分别为,已知.
(1)求边的长﹔
(2)在边上取一点,使得,求的值.
20.已知的内角A,B,C的对边分别为a,b,c,且.
(1)求角B的大小;
(2)若BC边上的高为,求.
21.记的内角,,所对的边分别为,,,已知,.
(1)求;
(2)在下列三个条件中选择一个作为补充条件,判断该三角形是否存在?若存在,求出三角形的面积;若不存在,说明理由.
①边上的中线长为,②边上的中线长为,③三角形的周长为.注:如果选择多个条件分别解答,按第一个解答计分.
22.在中,.
(1)求;
(2)再从条件①、条件②、条件③这三个条件中选择两个作为已知,使存在且唯一确定,求的面积.
条件①:;
条件②:;
条件③:.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】由正弦定理得到,结合倍角公式,求得,再利用诱导公式,即可求解.
【详解】在中,,
由正弦定理得,即,
由倍角公式得,,
解得,
,
故选:A
2.D
【分析】根据三角形有两个解,转化为以C为圆心,以2为半径的圆与BA有两个交点,再结合正弦定理求解.
【详解】如图所示:
因为AC=b=2,若三角形有两个解,
则以C为圆心,以2为半径的圆与BA有两个交点,
当时,圆与BA相切,不合题意;
当时,圆与BA交于B点,不合题意;
所以,且,
所以由正弦定理得:
,则,
解得,
故选:D
3.A
【分析】在三角形中由正弦定理,即可求出答案.
【详解】由正弦定理得.
或.,(舍).
故.
故选:A.
4.A
【分析】根据给定条件求出h值,再代值计算即可得解.
【详解】依题意,,则有,
,
所以晷影长为0.14.
故选:A
5.A
【分析】利用余弦定理推论得出a,b,c关系,在结合正弦定理边角互换列出方程,解出结果.
【详解】详解:由已知及正弦定理可得,由余弦定理推论可得
,故选A.
【点睛】本题考查正弦定理及余弦定理推论的应用.
6.B
【分析】在Rt△ADC中用CD表示AC,Rt△BDC中用CD表示BC,建立CD的方程求解即得.
【详解】Rt△ADC中,,则,Rt△BDC中,,则,
由AC-BC=AB得,约为米.
故选:B
7.D
【解析】根据,利用正弦定理得到求解.
【详解】因为在中,,
所以
因为,
所以,
因为则,
或
故选:D
8.B
【分析】先利用正弦定理将边转化成对应角的正弦值,再将转化成,展开化简即可.
【详解】已知等式利用正弦定理化简得:
∴
即
∴
∴
∴
∴,
即.
故选:B.
9.BC
【解析】由正余弦定理结合已知条件化简得,由三角形的面积公式结合基本不等式计算得面积的最大值.
【详解】∵,
∴,
∴,由正弦定理可得,
∴,,,
,当时取等号,
∴,∴.
故选:BC
【点睛】本题考查了正余弦定理的应用,三角形的面积公式,基本不等式求最值,属于基础题.
10.AC
【分析】利用余弦定理及基本不等式一一判断即可;
【详解】解:对于A选项,,可以得出,∴,故A正确;
对于B选项,因为,所以,当且仅当时取等号,因为,所以,故B错误;
对于C选项,假设,则,,则,所以与矛盾,∴,故C正确,
对于D选项,取,满足,此时,故D错误;
故选:AC.
11.CD
【解析】先利用正弦定理得到,再利用余弦定理和基本不等式得到,即可判断.
【详解】∵,
由正弦定理得:
∴,
∴,
当且仅当时取等号,
又,
故.
故选:CD.
【点睛】本题主要考查了正弦定理以及余弦定理,考查了基本不等式.属于较易题.
12.ABC
【分析】运用三角形的性质,结合正弦定理、余弦定理、三角形面积公式逐一判断即可.
【详解】解:对于选项:在中,若,根据大边对大角,所以,
利用正弦定理,所以,
则,故选项正确.
对于选项:在锐角三角形中,,即,
故不等式恒成立,故选项正确.
对于选项:在中,,
由余弦定理可知:,因此有
,即,因为,所以,
因此,所以或,即,或(舍去),
,所以,故C正确.
对于选项:在中,若,,三角形面积
所以,解得,
所以,
由正弦定理,故选项错误.
故选:.
13.
【分析】利用余弦定理解三角形求BC.
【详解】解:∵在中,,,,
∴由余弦定理可得:.
∴.
故答案为:.
14.
【分析】由三角形面积公式求得,再由余弦定理求得,最后由正弦定理计算可得.
【详解】解:,,的面积为,,解得,
由余弦定理得,,则,
由正弦定理,即,解得.
故答案为:.
15.
【分析】根据给定条件利用余弦定理计算作答.
【详解】在中,,AB=1,AC=2,由余弦定理得:
,则,
所以.
故答案为:
16.或
【分析】首先由正弦定理可求出,根据大边对大角的原则,由可得,即得解
【详解】由正弦定理得,
∴,
∵,∴,
∴或
故答案为:或
17.(1)或6;(2).
【分析】(1)利用余弦定理将化为,化简后再利用余弦定理可求出,由结合已知条件可求出a的值;
(2)由于,所以,可得,然后利用三角形的面积公式可求出面积,再利用面积法可求出边上的高的长
【详解】解:因为,所以,
所以,即.
由余弦定理可得,
因为,所以.
(1)因为,
所以,解得或6.
(2)因为,所以,
,
所以边上的高的长为.
18.(1)公里;(2)该流星不是地球蒸发物,而是“天外来客”,理由见解析.
【分析】(1)由已知条件在中利用正弦定理求出,在中再利用余弦定理求出,从而可得;
(2)由(1)求出的值可得流星发射点近似高度为3185公里,远远大于对流层最高近似高度18公里,从而可得结论
【详解】(1)因为,则,所以为等边角形,所以.
又因为,所以,所以,所以,,.在中,由正弦定理:,得, 解得,
在中,由余弦定理:
.
所以,所以公里.
(2)公里,所以流星发射点近似高度为3185公里,远远大于对流层最高近似高度18公里,所以该流星不是地球蒸发物,而是“天外来客”.(言之有理即可).
19.(1);(2).
【解析】(1)在中,利用余弦定理即可求解;
(2)在中,由正弦定理可以求出,再利用与互补可以求出,得出是钝角,从而可得为锐角,即可求出和的值,利用展开代入数值即可求解.
【详解】在中,因为,,,
由余弦定理,
得
所以解得:或(舍)
所以.
(2)在中,由正弦定理,
得.
所以
在中,因为,
所以为钝角.
而,
所以为锐角
故
因为,
所以,
,
【点睛】关键点点睛:本题解题的关键是利用两角互补余弦互为相反数求出,可得为钝角,从而为锐角,可确定的值.
20.(1)
(2)
【分析】(1)先根据式子形式采取角化边,然后利用余弦定理的推论即可解出;
(2)先根据锐角三角函数的定义可知,,得出关系,再根据可求出,然后根据三角形内角和定理,诱导公式,两角和的正弦公式化简,即可解出.
【详解】(1)由,得,即,∴,∵,∴.
(2)∵,且BC边上的高为,∴,∴,
∴.∵,∴C为锐角,∴,
∴.
21.(1)
(2)选①,三角形不存在;选②,三角形存在,面积为;选③,三角形存在,面积为
【分析】(1)利用三角形内角和与三角恒等变换化简求值;
(2)选①,方法一:由,在,,分别用余弦定理可得方程组,求解即可;方法二:由,平方,结合向量数量积公式解方程;方法三:建立平面直角坐标系,结合中点公式及两点间距离可得方程,求解;选②,在中利用余弦定理,可解得,进而可得面积;选③,在中用余弦定理,结合周长,可解得各边长,进而求得面积.
(1)由得,又,所以,而,故,故;
(2)选①,方法一:设边上的中线为,则,由得,,即,即,由余弦定理得,即,该方程无实数解,故符合条件的三角形不存在.方法二:设边上的中线为,则,两边平方得,即,即,易知该方程无实数解,故符合条件的三角形不存在.方法三:如图,以为原点,所在直线为轴,建立直角坐标系.故点坐标为,即,点坐标为,所以边的中点坐标为, 由边上的中线长为得,整理得,该方程无实数解,故符合条件的三角形不存在.选②,设边上的中线为,则.在中,由余弦定理得,即,整理得,解得或(舍去),故的面积.选③,依题意得,由(1)知,所以,在中,由余弦定理得,,所以,即, 所以,解得,,所以的面积.
22.(1)
(2)1
【分析】(1)利用正弦定理将已知条件边化角,化简即可.
(2) 若选择①②,可以确定的三个角,但无法确定边长,不符合题意;
若选②③,利用正弦定理求边长,根据角度关系求,即可求出面积;
若选①③,利用余弦定理求边长,再求出,即可求面积.
(1)
因为,
由正弦定理可得,
因为,所以,即,
因为,则;
(2)
若选择①②,由,可得,由于已知条件未给出任意一边的长度,满足条件的三角形有无数个,并不唯一确定,不符合题意.
若选择②③,由正弦定理,及,,得,所以,
因为,所以,,
,
所以.
若选择①③,由余弦定理得,及,
得,解得,
所以,所以.
答案第1页,共2页
答案第1页,共2页
1.人们通常把顶角为36°的等腰三角形称为黄金三角形,因为它的底边和腰长的比值等于黄金分割比,我们熟悉的五角星就是由5个黄金三角形和1个正五边形组成的,如图,三角形ABC就是一个黄金三角形,根据以上信息,可得=( )
A. B. C. D.
2.已知在ABC中,a=x,b=2,B=30°,若三角形有两解,则x的取值范围是( )
A.x>2 B.0
A. B. C.或 D.无解
4.唐代数学家、天文学家僧一行,利用“九服晷影算法”建立了从0°到80°的晷影长l与太阳天顶距θ的对应数表.已知晷影长l、表高h与太阳天顶距θ满足l=htanθ,当晷影长为0.7时,天顶距为5°.若天顶距为1°时,则晷影长为( )(参考数据:tan1°≈0.0175,tan3°≈0.0349,tan5°≈0.0875)
A.0.14 B.0.16 C.0.18 D.0.24
5.△ABC的内角A,B,C的对边分别为a,b,c,已知asinA-bsinB=4csinC,cosA=-,则=
A.6 B.5 C.4 D.3
6.岳阳楼与湖北武汉黄鹤楼,江西南昌滕王阁并称为“江南三大名楼”,是“中国十大历史文化名楼”之一,世称“天下第一楼”.其地处岳阳古城西门城墙之上,紧靠洞庭湖畔,下瞰洞庭,前望君山.始建于东汉建安二十年(215年),历代屡加重修,现存建筑沿袭清光绪六年(1880年)重建时的形制与格局.因北宋滕宗谅重修岳阳楼,邀好友范仲淹作《岳阳楼记》使得岳阳楼著称于世.自古有"洞庭天下水,岳阳天下楼"之美誉.小李为测量岳阳楼的高度选取了与底部水平的直线,如图,测得,,米,则岳阳楼的高度约为(,)( )
A.米 B.米 C.米 D.米
7.在中,角所对的边分别为,若,则( )
A. B.或 C. D.或
8.已知a、b、c分别为△ABC的三内角A、B、C的对边,,则( )
A. B. C. D.
二、多选题
9.已知,,分别为内角,,的对边,,且,则下列结论中正确的是( )
A. B.
C.面积的最大值为 D.面积的最大值为
10.设的内角、、所对边的长分别为、、,下列命题正确的是( )
A.若,则
B.若,则
C.若,则
D.若,则
11.已知中,角,,的对边分别为,,,且,则角的值不可能是( )
A.45° B.60° C.75° D.90°
12.下列结论正确的是( )
A.在中,若,则
B.在锐角三角形中,不等式恒成立
C.在中,若,,则为等腰直角三角形
D.在中,若,,三角形面积,则三角形外接圆半径为
三、填空题
13.在中,,,,那么的长度为______.
14.在中,内角A,B,C所对边分别为a,b,c.若的面积为,则__________.
15.在中,∠A=60°,AB=1,AC=2,则BC=___________.
16.在中,若,则的大小为__________.
四、解答题
17.在中,A,B,C的对边分别是a,b,c,且.
(1)求a的值;
(2)若,求边上的高的长.
18.仰望星空,时有流星划过天际,令我们感叹生命的短暂,又深深震撼我们凡俗的心灵.流星是什么?从古至今,人们作过无数种猜测.古希腊亚里士多德说,那是地球上的蒸发物,近代有人进一步认为,那是地球上磷火升空后的燃烧现象.10世纪波斯著名数学家、天文学家阿尔·库希设计出一种方案,通过两个观测者异地同时观察同一颗流星,来测定其发射点的高度.如图,假设地球是一个标准的球体,为地球的球心,为地平线,有两个观测者在地球上的,两地同时观测到一颗流星,观测的仰角分别为,,其中,,为了方便计算,我们考虑一种理想状态,假设两个观测者在地球上的,两点测得,,地球半径为公里,两个观测者的距离 .(参考数据:,)
(1)求流星发射点近似高度;
(2)在古希腊,科学不发达,人们看到流星以为这是地球水分蒸发后凝结的固体,已知对流层高度大约在18公里左右,若地球半径公里,请你据此判断该流星是地球蒸发物还是“天外来客”?并说明理由.
19.在中,角的对边分别为,已知.
(1)求边的长﹔
(2)在边上取一点,使得,求的值.
20.已知的内角A,B,C的对边分别为a,b,c,且.
(1)求角B的大小;
(2)若BC边上的高为,求.
21.记的内角,,所对的边分别为,,,已知,.
(1)求;
(2)在下列三个条件中选择一个作为补充条件,判断该三角形是否存在?若存在,求出三角形的面积;若不存在,说明理由.
①边上的中线长为,②边上的中线长为,③三角形的周长为.注:如果选择多个条件分别解答,按第一个解答计分.
22.在中,.
(1)求;
(2)再从条件①、条件②、条件③这三个条件中选择两个作为已知,使存在且唯一确定,求的面积.
条件①:;
条件②:;
条件③:.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】由正弦定理得到,结合倍角公式,求得,再利用诱导公式,即可求解.
【详解】在中,,
由正弦定理得,即,
由倍角公式得,,
解得,
,
故选:A
2.D
【分析】根据三角形有两个解,转化为以C为圆心,以2为半径的圆与BA有两个交点,再结合正弦定理求解.
【详解】如图所示:
因为AC=b=2,若三角形有两个解,
则以C为圆心,以2为半径的圆与BA有两个交点,
当时,圆与BA相切,不合题意;
当时,圆与BA交于B点,不合题意;
所以,且,
所以由正弦定理得:
,则,
解得,
故选:D
3.A
【分析】在三角形中由正弦定理,即可求出答案.
【详解】由正弦定理得.
或.,(舍).
故.
故选:A.
4.A
【分析】根据给定条件求出h值,再代值计算即可得解.
【详解】依题意,,则有,
,
所以晷影长为0.14.
故选:A
5.A
【分析】利用余弦定理推论得出a,b,c关系,在结合正弦定理边角互换列出方程,解出结果.
【详解】详解:由已知及正弦定理可得,由余弦定理推论可得
,故选A.
【点睛】本题考查正弦定理及余弦定理推论的应用.
6.B
【分析】在Rt△ADC中用CD表示AC,Rt△BDC中用CD表示BC,建立CD的方程求解即得.
【详解】Rt△ADC中,,则,Rt△BDC中,,则,
由AC-BC=AB得,约为米.
故选:B
7.D
【解析】根据,利用正弦定理得到求解.
【详解】因为在中,,
所以
因为,
所以,
因为则,
或
故选:D
8.B
【分析】先利用正弦定理将边转化成对应角的正弦值,再将转化成,展开化简即可.
【详解】已知等式利用正弦定理化简得:
∴
即
∴
∴
∴
∴,
即.
故选:B.
9.BC
【解析】由正余弦定理结合已知条件化简得,由三角形的面积公式结合基本不等式计算得面积的最大值.
【详解】∵,
∴,
∴,由正弦定理可得,
∴,,,
,当时取等号,
∴,∴.
故选:BC
【点睛】本题考查了正余弦定理的应用,三角形的面积公式,基本不等式求最值,属于基础题.
10.AC
【分析】利用余弦定理及基本不等式一一判断即可;
【详解】解:对于A选项,,可以得出,∴,故A正确;
对于B选项,因为,所以,当且仅当时取等号,因为,所以,故B错误;
对于C选项,假设,则,,则,所以与矛盾,∴,故C正确,
对于D选项,取,满足,此时,故D错误;
故选:AC.
11.CD
【解析】先利用正弦定理得到,再利用余弦定理和基本不等式得到,即可判断.
【详解】∵,
由正弦定理得:
∴,
∴,
当且仅当时取等号,
又,
故.
故选:CD.
【点睛】本题主要考查了正弦定理以及余弦定理,考查了基本不等式.属于较易题.
12.ABC
【分析】运用三角形的性质,结合正弦定理、余弦定理、三角形面积公式逐一判断即可.
【详解】解:对于选项:在中,若,根据大边对大角,所以,
利用正弦定理,所以,
则,故选项正确.
对于选项:在锐角三角形中,,即,
故不等式恒成立,故选项正确.
对于选项:在中,,
由余弦定理可知:,因此有
,即,因为,所以,
因此,所以或,即,或(舍去),
,所以,故C正确.
对于选项:在中,若,,三角形面积
所以,解得,
所以,
由正弦定理,故选项错误.
故选:.
13.
【分析】利用余弦定理解三角形求BC.
【详解】解:∵在中,,,,
∴由余弦定理可得:.
∴.
故答案为:.
14.
【分析】由三角形面积公式求得,再由余弦定理求得,最后由正弦定理计算可得.
【详解】解:,,的面积为,,解得,
由余弦定理得,,则,
由正弦定理,即,解得.
故答案为:.
15.
【分析】根据给定条件利用余弦定理计算作答.
【详解】在中,,AB=1,AC=2,由余弦定理得:
,则,
所以.
故答案为:
16.或
【分析】首先由正弦定理可求出,根据大边对大角的原则,由可得,即得解
【详解】由正弦定理得,
∴,
∵,∴,
∴或
故答案为:或
17.(1)或6;(2).
【分析】(1)利用余弦定理将化为,化简后再利用余弦定理可求出,由结合已知条件可求出a的值;
(2)由于,所以,可得,然后利用三角形的面积公式可求出面积,再利用面积法可求出边上的高的长
【详解】解:因为,所以,
所以,即.
由余弦定理可得,
因为,所以.
(1)因为,
所以,解得或6.
(2)因为,所以,
,
所以边上的高的长为.
18.(1)公里;(2)该流星不是地球蒸发物,而是“天外来客”,理由见解析.
【分析】(1)由已知条件在中利用正弦定理求出,在中再利用余弦定理求出,从而可得;
(2)由(1)求出的值可得流星发射点近似高度为3185公里,远远大于对流层最高近似高度18公里,从而可得结论
【详解】(1)因为,则,所以为等边角形,所以.
又因为,所以,所以,所以,,.在中,由正弦定理:,得, 解得,
在中,由余弦定理:
.
所以,所以公里.
(2)公里,所以流星发射点近似高度为3185公里,远远大于对流层最高近似高度18公里,所以该流星不是地球蒸发物,而是“天外来客”.(言之有理即可).
19.(1);(2).
【解析】(1)在中,利用余弦定理即可求解;
(2)在中,由正弦定理可以求出,再利用与互补可以求出,得出是钝角,从而可得为锐角,即可求出和的值,利用展开代入数值即可求解.
【详解】在中,因为,,,
由余弦定理,
得
所以解得:或(舍)
所以.
(2)在中,由正弦定理,
得.
所以
在中,因为,
所以为钝角.
而,
所以为锐角
故
因为,
所以,
,
【点睛】关键点点睛:本题解题的关键是利用两角互补余弦互为相反数求出,可得为钝角,从而为锐角,可确定的值.
20.(1)
(2)
【分析】(1)先根据式子形式采取角化边,然后利用余弦定理的推论即可解出;
(2)先根据锐角三角函数的定义可知,,得出关系,再根据可求出,然后根据三角形内角和定理,诱导公式,两角和的正弦公式化简,即可解出.
【详解】(1)由,得,即,∴,∵,∴.
(2)∵,且BC边上的高为,∴,∴,
∴.∵,∴C为锐角,∴,
∴.
21.(1)
(2)选①,三角形不存在;选②,三角形存在,面积为;选③,三角形存在,面积为
【分析】(1)利用三角形内角和与三角恒等变换化简求值;
(2)选①,方法一:由,在,,分别用余弦定理可得方程组,求解即可;方法二:由,平方,结合向量数量积公式解方程;方法三:建立平面直角坐标系,结合中点公式及两点间距离可得方程,求解;选②,在中利用余弦定理,可解得,进而可得面积;选③,在中用余弦定理,结合周长,可解得各边长,进而求得面积.
(1)由得,又,所以,而,故,故;
(2)选①,方法一:设边上的中线为,则,由得,,即,即,由余弦定理得,即,该方程无实数解,故符合条件的三角形不存在.方法二:设边上的中线为,则,两边平方得,即,即,易知该方程无实数解,故符合条件的三角形不存在.方法三:如图,以为原点,所在直线为轴,建立直角坐标系.故点坐标为,即,点坐标为,所以边的中点坐标为, 由边上的中线长为得,整理得,该方程无实数解,故符合条件的三角形不存在.选②,设边上的中线为,则.在中,由余弦定理得,即,整理得,解得或(舍去),故的面积.选③,依题意得,由(1)知,所以,在中,由余弦定理得,,所以,即, 所以,解得,,所以的面积.
22.(1)
(2)1
【分析】(1)利用正弦定理将已知条件边化角,化简即可.
(2) 若选择①②,可以确定的三个角,但无法确定边长,不符合题意;
若选②③,利用正弦定理求边长,根据角度关系求,即可求出面积;
若选①③,利用余弦定理求边长,再求出,即可求面积.
(1)
因为,
由正弦定理可得,
因为,所以,即,
因为,则;
(2)
若选择①②,由,可得,由于已知条件未给出任意一边的长度,满足条件的三角形有无数个,并不唯一确定,不符合题意.
若选择②③,由正弦定理,及,,得,所以,
因为,所以,,
,
所以.
若选择①③,由余弦定理得,及,
得,解得,
所以,所以.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
