4.3 线段的长短比较 课件 (共25张PPT)
文档属性
| 名称 | 4.3 线段的长短比较 课件 (共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-06 00:00:00 | ||
图片预览




文档简介
(共25张PPT)
沪科版 七年级上册
4.3 线段的长短比较
课件说明
1.知道比较线段长短的两种方法.
教学目标
2.掌握线段中点的定义.
教学重点:
线段中点的定义及表示方法.
3.知道线段的性质及两点间距离的定义.
A
B
C
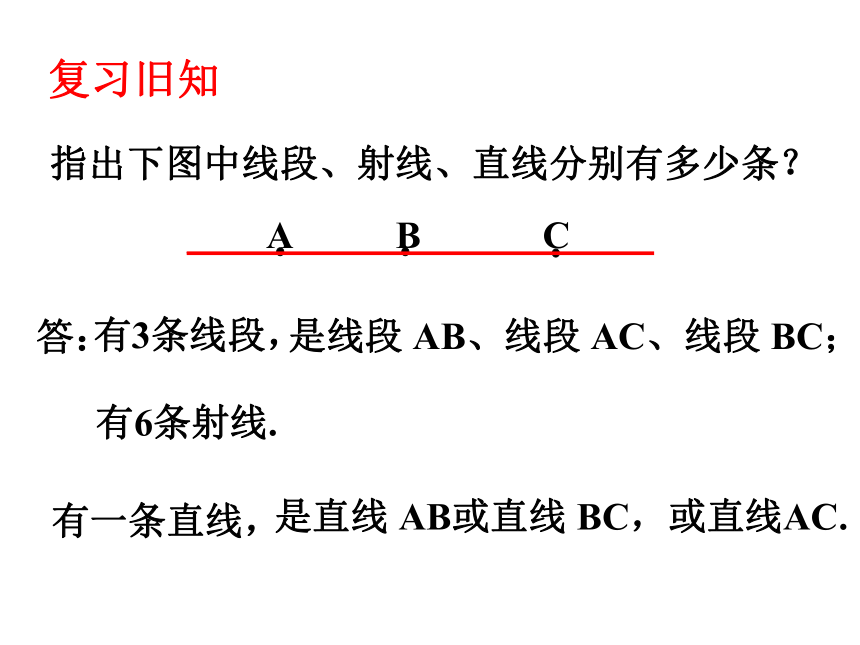
指出下图中线段、射线、直线分别有多少条?
答:
有3条线段,
有6条射线.
有一条直线,
是线段 AB、线段 AC、线段 BC;
是直线 AB或直线 BC,或直线AC.
复习旧知
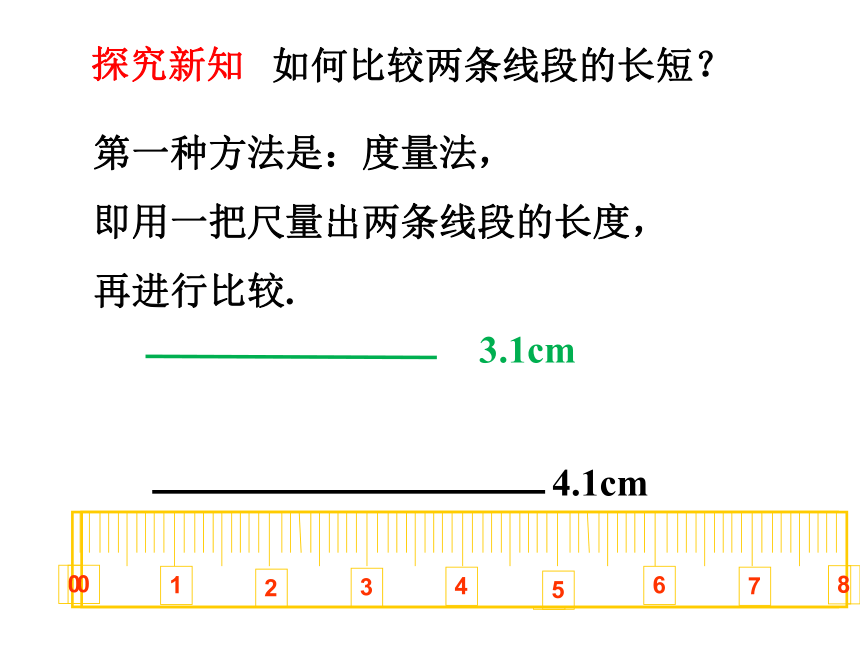
第一种方法是:度量法,
即用一把尺量出两条线段的长度,
再进行比较.
1
2
3
5
4
6
7
8
0
3.1cm
4.1cm
1
2
3
5
4
6
7
8
0
如何比较两条线段的长短?
探究新知
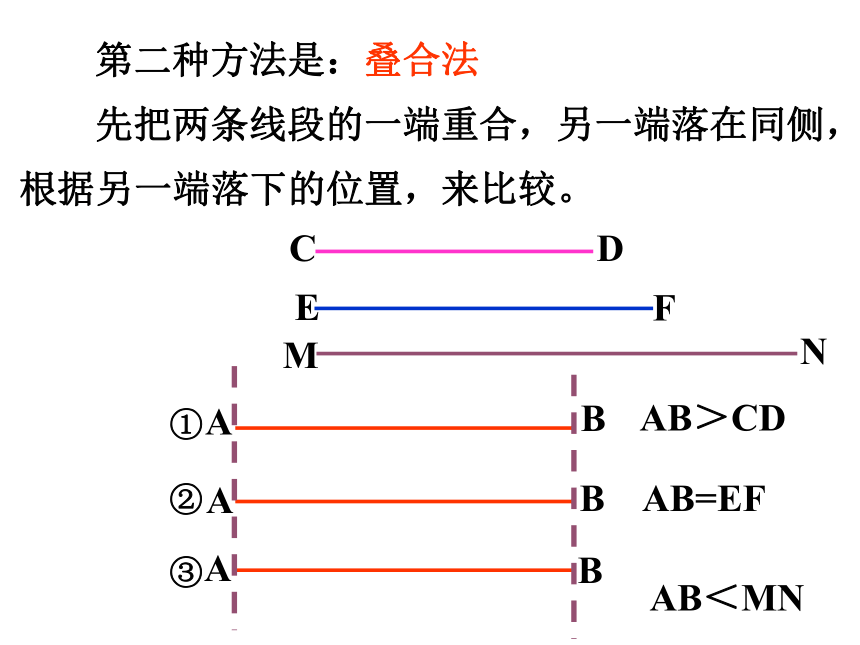
第二种方法是:叠合法
先把两条线段的一端重合,另一端落在同侧,
根据另一端落下的位置,来比较。
①
②
③
A
B
B
A
A
B
C
D
E
F
M
N
AB>CD
AB=EF
AB<MN
a
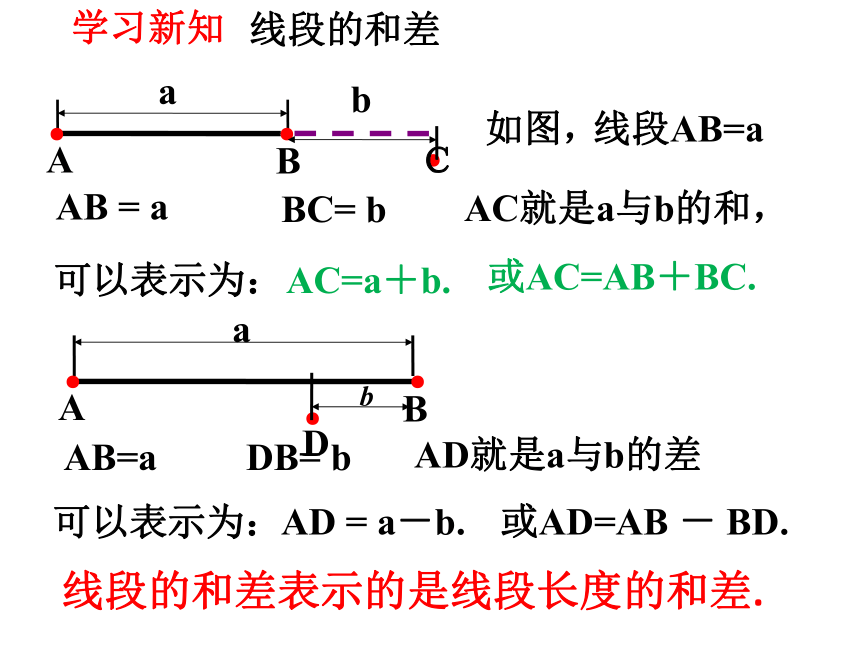
线段的和差
如图,
线段AB=a
●
C
●
●
A
B
a
AB = a
b
BC= b
AC=a+b.
●
●
A
B
●
AB=a
D
b
DB= b
AD = a-b.
AC就是a与b的和,
AD就是a与b的差
可以表示为:
可以表示为:
线段的和差表示的是线段长度的和差.
或AC=AB+BC.
或AD=AB - BD.
学习新知
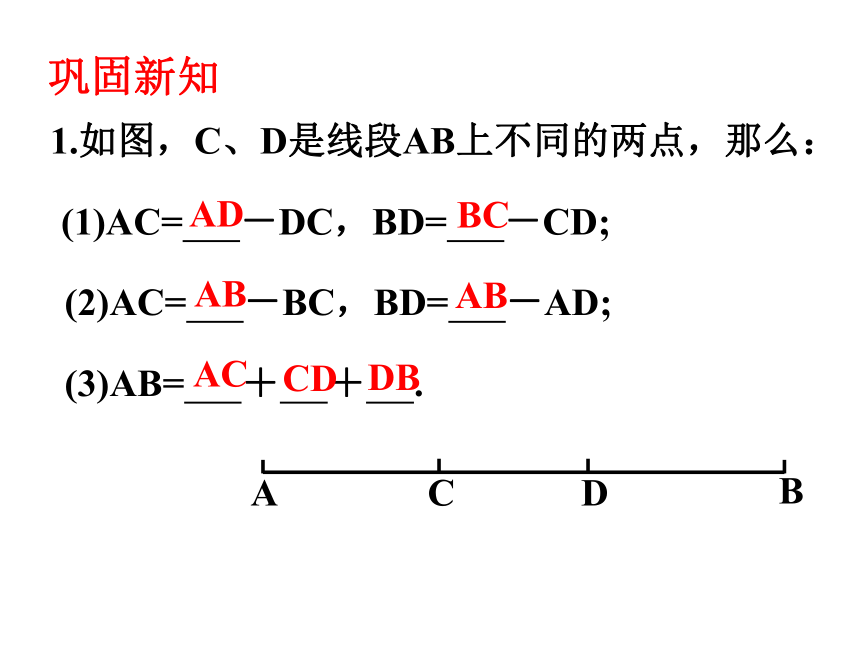
1.如图,C、D是线段AB上不同的两点,那么:
(1)AC= -DC,BD= -CD;
(2)AC= -BC,BD= -AD;
(3)AB= + + .
A
C
D
B
AD
BC
AB
AB
AC
CD
DB
巩固新知
2.已知线段AB=12cm,在直线AB上画线段BC,
使BC=7cm,求线段AC的长.
②当端点C在线段AB的延长线上时,
①端点C在线段AB上时,
解:
AC=
AC=
AB-BC
=
12cm-7cm
=5cm
=19cm
12cm+7cm
AB+BC
=
A
B
C
C
A
B
A
B
C
∴AC=
BC,
-
2
1
AB,
(或∴AB=2AC,
∵点C是线段AB的中点,
几何符号语言:
AB=2BC)
如图,点C在线段AB 上且使线段AC,CB相等,这样的点C叫做线段AB的中点.
AC=
-
2
1
AB,
BC=
学习新知
如图,点C是线段AB的中点
(1) 若AB=10cm,则AC= cm.
(2) 若AC=10cm,则AB= cm.
5
20
A
B
C
巩固新知
●
●
A
B
例 已知:线段AB=4,延长AB至点C,使AC
=11.点D是AB的中点,点E是AC的中点.求DE的长.
解:如图,
●
●
●
D
E
C
∵AC=11,点E为AC中点,
∵AB=4,点D为AB的中点,
=5.5-2
=3.5.
∴DE=AE-AD
∴AD=
∴AE=
AB
=2
1
2
1
2
×4
=
AC
=5.5
1
2
1
2
×11
=
如图,点D是线段AB的中点,C是线段AD
的中点,若AB=20cm,求线段CD 的长度.
解:
∵
点D是线段AB的中点,
AD=
AB
=10cm.
20cm
1
2
1
2
×
∴
=
∵
点C是线段AD的中点,
CD=
AD
=5cm.
10cm
1
2
1
2
×
∴
=
A
C
D
B
练习巩固
甲
乙
1.如图,甲、乙两地间有曲线、折线、线段等4条路可走其中哪条路最短?
2.如图,人们修建公路遇到大山阻碍时,为什么时常打通一条穿越大山的直的隧道?
探究新知
结论:
1.线段的基本事实:
两点之间的所有连线中,线段最短.
两点之间线段的长度,叫做这两点之间的距离.
2.两点之间的距离:
甲
乙
1.如图 ,A,B两个村庄在一条河l(不计河的宽度)的两侧,现要建一座码头,使它到 A,B 两个村庄的距离之和最小.如图,连接AB,与l交于点C,则点C即为所求的码头的位置,这样做的理由是( ).
巩固新知
A.经过 两点有且只有一条直线
B. 两条直线相交只有一个交点
C.两点之间的所有连线中,线段最短
D.经过一点有无数条直线
l
A
B
C
C
2.某地有A,B,C,D四个村庄,为解决当地的缺水问题,政府准备修建一个储水池,不考虑其他因素,请你画出储水池P的位置,使它与四个村庄的距离之和最小.
A
B
D
C
解:
连接AC,
连接BD,
AC与BD的交点就是
所求储水池P的位置.
P
本节课你有哪些收获?
(3)知道了线段的基本事实:
(1)掌握了线段长短的比较方法.
(4)知道了两点之间的距离的概念.
课堂小结
①叠合法,②度量法.
两点之间的所有连线中,线段最短.
两点之间线段的长度,叫做这两点之间的距离.
(2)知道了线段的中点的概念.
如果点C在线段AB上且使线段AC,CB相等,这样的点C叫做线段AB的中点.
1.如图,点C,D,E是线段AB上的三个点,
下面是关于线段CE的表示:
①CE=CD+DE;②CE=BC-EB;
③CE=CD+BD-AC;④ CE=AE+BC-AB.
其中正确的是 (填序号).
巩固提高
A
B
E
D
C
①
②
④
2.如图,C,D是线段AB上两点,D是AC的中点,CB=4cm,DB=7cm,求AB,AC的长.
A
B
D
C
解:
∵点D是线段AC的中点,
∴AC=2DC=6cm.
∵CB=4cm,DB=7cm,
∴DC=
DB-CB
=7cm-4cm
=3cm.
AB=AC+CB=6cm+4cm=10cm.
3.同一条直线上有A,B,C,D,E,F六个点,且C是AB的中点,B是AD的中点,A是BE的中点,D是EF的中点,AC=1,求EF的长.
∵C是AB的中点,AC=1,
∵B是AD的中点,
∵A是BE的中点,
∴ED=EB+BD=4+2=6,
解:
如图,
E
F
B
D
A
C
∴AB=2AC=2,
∴AB=BD=2;
∴BE=2AB=2×2=4,
∴EF=2ED=2×6=12.
∵D是EF的中点 ,
4.线段AB上有两点P,Q,点P将AB分成两部分,AP:PB=2:3;点Q将AB分成两部分,AQ:QB=4:1;且PQ=3cm,求AP,QB的长.
A
B
P
Q
解:
如图,
设AP=2xcm,
QB=ycm,
则PB=3xcm,
AQ=4ycm,
2x+3=4y ①
3x-3=y ②
解这个方程组,得
x=
y=
1.5,
1.5.
根据题意,得
∴AP=2x=3cm,
QB=1.5cm.
5.如图所示,B,C是线段AD上任意两点,M是AB的中点,N是CD中点,若MN=a,BC=b,则线段 AD 的长是( ).
A. 2(a-b) B.2a-b C. a+b D.a-b
A
D
B
C
M
N
B
今天作业
课本P142页第2、3、4 题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 七年级上册
4.3 线段的长短比较
课件说明
1.知道比较线段长短的两种方法.
教学目标
2.掌握线段中点的定义.
教学重点:
线段中点的定义及表示方法.
3.知道线段的性质及两点间距离的定义.
A
B
C
指出下图中线段、射线、直线分别有多少条?
答:
有3条线段,
有6条射线.
有一条直线,
是线段 AB、线段 AC、线段 BC;
是直线 AB或直线 BC,或直线AC.
复习旧知
第一种方法是:度量法,
即用一把尺量出两条线段的长度,
再进行比较.
1
2
3
5
4
6
7
8
0
3.1cm
4.1cm
1
2
3
5
4
6
7
8
0
如何比较两条线段的长短?
探究新知
第二种方法是:叠合法
先把两条线段的一端重合,另一端落在同侧,
根据另一端落下的位置,来比较。
①
②
③
A
B
B
A
A
B
C
D
E
F
M
N
AB>CD
AB=EF
AB<MN
a
线段的和差
如图,
线段AB=a
●
C
●
●
A
B
a
AB = a
b
BC= b
AC=a+b.
●
●
A
B
●
AB=a
D
b
DB= b
AD = a-b.
AC就是a与b的和,
AD就是a与b的差
可以表示为:
可以表示为:
线段的和差表示的是线段长度的和差.
或AC=AB+BC.
或AD=AB - BD.
学习新知
1.如图,C、D是线段AB上不同的两点,那么:
(1)AC= -DC,BD= -CD;
(2)AC= -BC,BD= -AD;
(3)AB= + + .
A
C
D
B
AD
BC
AB
AB
AC
CD
DB
巩固新知
2.已知线段AB=12cm,在直线AB上画线段BC,
使BC=7cm,求线段AC的长.
②当端点C在线段AB的延长线上时,
①端点C在线段AB上时,
解:
AC=
AC=
AB-BC
=
12cm-7cm
=5cm
=19cm
12cm+7cm
AB+BC
=
A
B
C
C
A
B
A
B
C
∴AC=
BC,
-
2
1
AB,
(或∴AB=2AC,
∵点C是线段AB的中点,
几何符号语言:
AB=2BC)
如图,点C在线段AB 上且使线段AC,CB相等,这样的点C叫做线段AB的中点.
AC=
-
2
1
AB,
BC=
学习新知
如图,点C是线段AB的中点
(1) 若AB=10cm,则AC= cm.
(2) 若AC=10cm,则AB= cm.
5
20
A
B
C
巩固新知
●
●
A
B
例 已知:线段AB=4,延长AB至点C,使AC
=11.点D是AB的中点,点E是AC的中点.求DE的长.
解:如图,
●
●
●
D
E
C
∵AC=11,点E为AC中点,
∵AB=4,点D为AB的中点,
=5.5-2
=3.5.
∴DE=AE-AD
∴AD=
∴AE=
AB
=2
1
2
1
2
×4
=
AC
=5.5
1
2
1
2
×11
=
如图,点D是线段AB的中点,C是线段AD
的中点,若AB=20cm,求线段CD 的长度.
解:
∵
点D是线段AB的中点,
AD=
AB
=10cm.
20cm
1
2
1
2
×
∴
=
∵
点C是线段AD的中点,
CD=
AD
=5cm.
10cm
1
2
1
2
×
∴
=
A
C
D
B
练习巩固
甲
乙
1.如图,甲、乙两地间有曲线、折线、线段等4条路可走其中哪条路最短?
2.如图,人们修建公路遇到大山阻碍时,为什么时常打通一条穿越大山的直的隧道?
探究新知
结论:
1.线段的基本事实:
两点之间的所有连线中,线段最短.
两点之间线段的长度,叫做这两点之间的距离.
2.两点之间的距离:
甲
乙
1.如图 ,A,B两个村庄在一条河l(不计河的宽度)的两侧,现要建一座码头,使它到 A,B 两个村庄的距离之和最小.如图,连接AB,与l交于点C,则点C即为所求的码头的位置,这样做的理由是( ).
巩固新知
A.经过 两点有且只有一条直线
B. 两条直线相交只有一个交点
C.两点之间的所有连线中,线段最短
D.经过一点有无数条直线
l
A
B
C
C
2.某地有A,B,C,D四个村庄,为解决当地的缺水问题,政府准备修建一个储水池,不考虑其他因素,请你画出储水池P的位置,使它与四个村庄的距离之和最小.
A
B
D
C
解:
连接AC,
连接BD,
AC与BD的交点就是
所求储水池P的位置.
P
本节课你有哪些收获?
(3)知道了线段的基本事实:
(1)掌握了线段长短的比较方法.
(4)知道了两点之间的距离的概念.
课堂小结
①叠合法,②度量法.
两点之间的所有连线中,线段最短.
两点之间线段的长度,叫做这两点之间的距离.
(2)知道了线段的中点的概念.
如果点C在线段AB上且使线段AC,CB相等,这样的点C叫做线段AB的中点.
1.如图,点C,D,E是线段AB上的三个点,
下面是关于线段CE的表示:
①CE=CD+DE;②CE=BC-EB;
③CE=CD+BD-AC;④ CE=AE+BC-AB.
其中正确的是 (填序号).
巩固提高
A
B
E
D
C
①
②
④
2.如图,C,D是线段AB上两点,D是AC的中点,CB=4cm,DB=7cm,求AB,AC的长.
A
B
D
C
解:
∵点D是线段AC的中点,
∴AC=2DC=6cm.
∵CB=4cm,DB=7cm,
∴DC=
DB-CB
=7cm-4cm
=3cm.
AB=AC+CB=6cm+4cm=10cm.
3.同一条直线上有A,B,C,D,E,F六个点,且C是AB的中点,B是AD的中点,A是BE的中点,D是EF的中点,AC=1,求EF的长.
∵C是AB的中点,AC=1,
∵B是AD的中点,
∵A是BE的中点,
∴ED=EB+BD=4+2=6,
解:
如图,
E
F
B
D
A
C
∴AB=2AC=2,
∴AB=BD=2;
∴BE=2AB=2×2=4,
∴EF=2ED=2×6=12.
∵D是EF的中点 ,
4.线段AB上有两点P,Q,点P将AB分成两部分,AP:PB=2:3;点Q将AB分成两部分,AQ:QB=4:1;且PQ=3cm,求AP,QB的长.
A
B
P
Q
解:
如图,
设AP=2xcm,
QB=ycm,
则PB=3xcm,
AQ=4ycm,
2x+3=4y ①
3x-3=y ②
解这个方程组,得
x=
y=
1.5,
1.5.
根据题意,得
∴AP=2x=3cm,
QB=1.5cm.
5.如图所示,B,C是线段AD上任意两点,M是AB的中点,N是CD中点,若MN=a,BC=b,则线段 AD 的长是( ).
A. 2(a-b) B.2a-b C. a+b D.a-b
A
D
B
C
M
N
B
今天作业
课本P142页第2、3、4 题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
