4.5 角的比较与补(余)角(1) 课件(共25张PPT)
文档属性
| 名称 | 4.5 角的比较与补(余)角(1) 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-05 00:00:00 | ||
图片预览


文档简介
(共25张PPT)
沪科版 七年级上册
4.5 角的比较与补(余)角(1)
课件说明
1.知道比较角的大小的两种方法;
教学目标
2.掌握角平分线的定义.
教学重点:
角平分线的定义及表示方法.
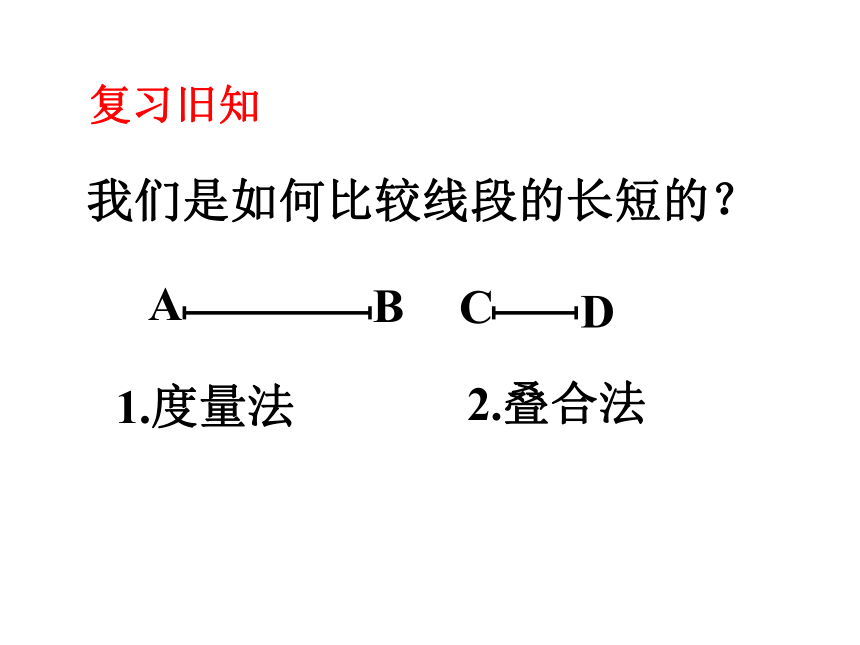
我们是如何比较线段的长短的?
A
B
C
D
1.度量法
2.叠合法
复习旧知
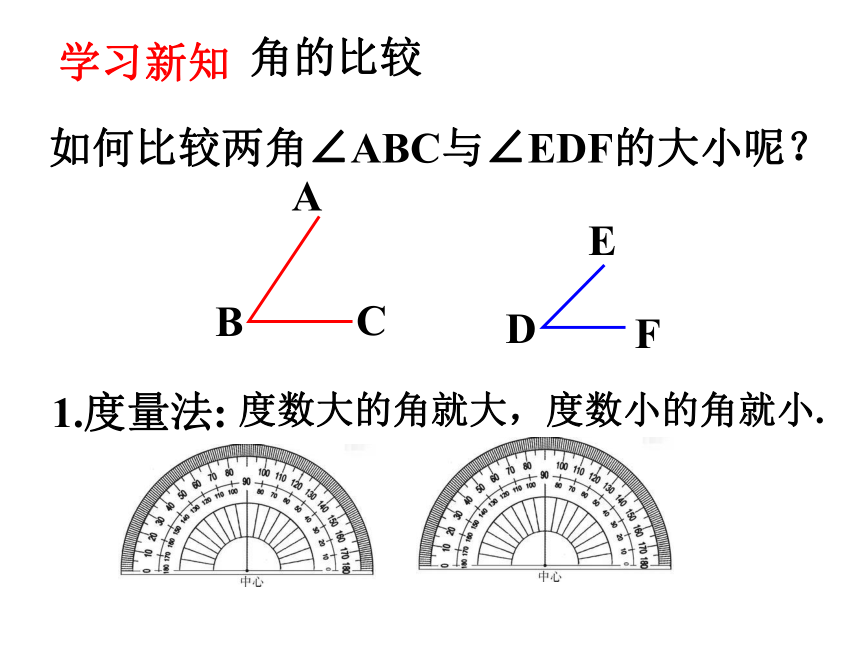
角的比较
如何比较两角∠ABC与∠EDF的大小呢?
1.度量法:
度数大的角就大,度数小的角就小.
A
B
C
E
D
F
学习新知
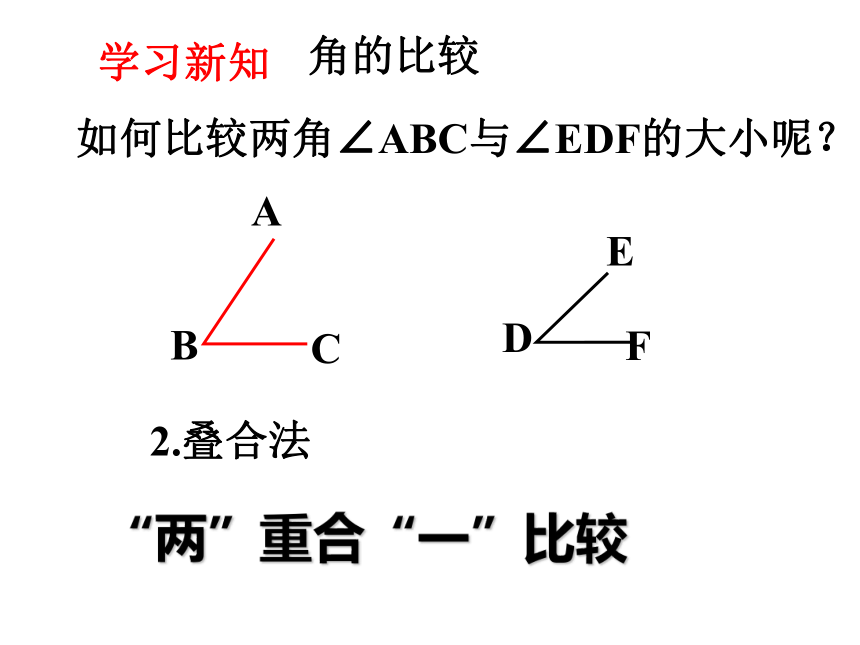
角的比较
如何比较两角∠ABC与∠EDF的大小呢?
A
B
C
E
D
F
2.叠合法
“两”重合“一”比较
学习新知
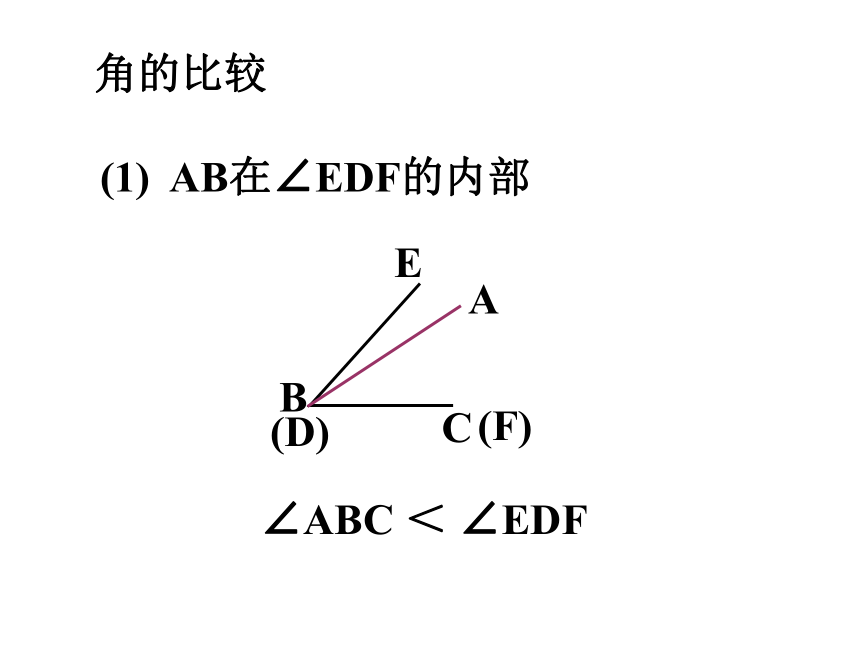
(1) AB在∠EDF的内部
∠ABC < ∠EDF
C
A
B
(F)
(D)
E
角的比较
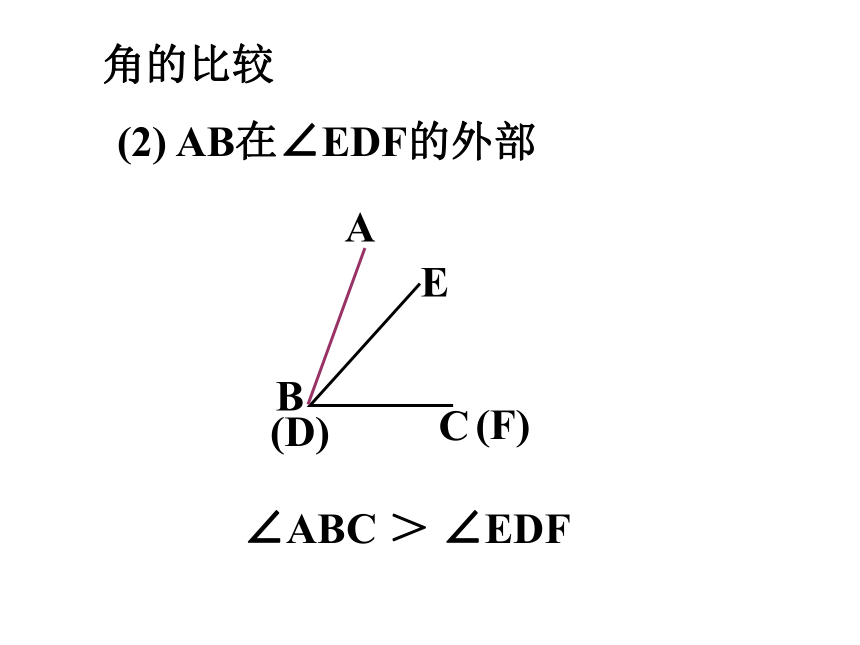
(2) AB在∠EDF的外部
C
A
B
(F)
(D)
E
∠ABC > ∠EDF
角的比较
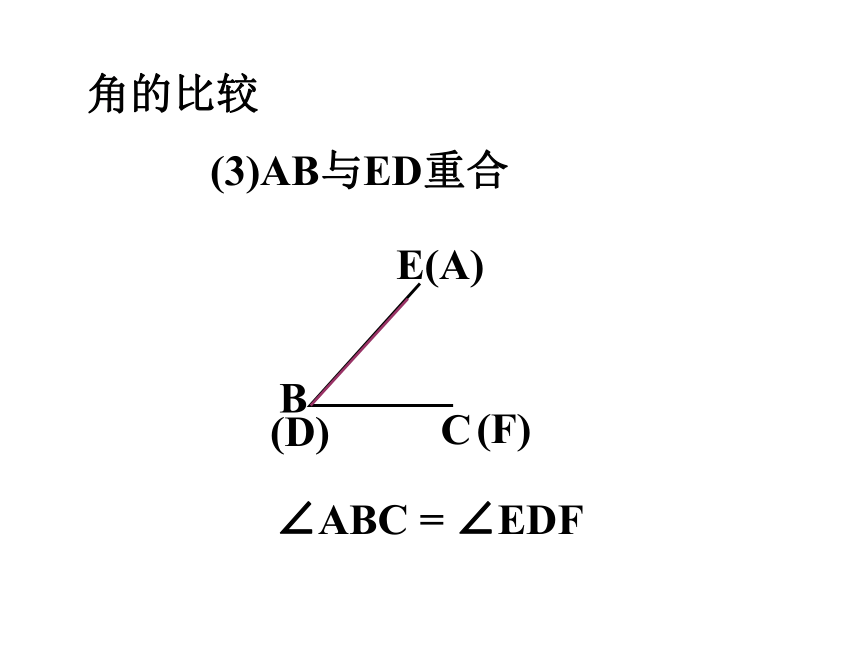
(3)AB与ED重合
(F)
C
B
E(A)
(D)
∠ABC = ∠EDF
角的比较
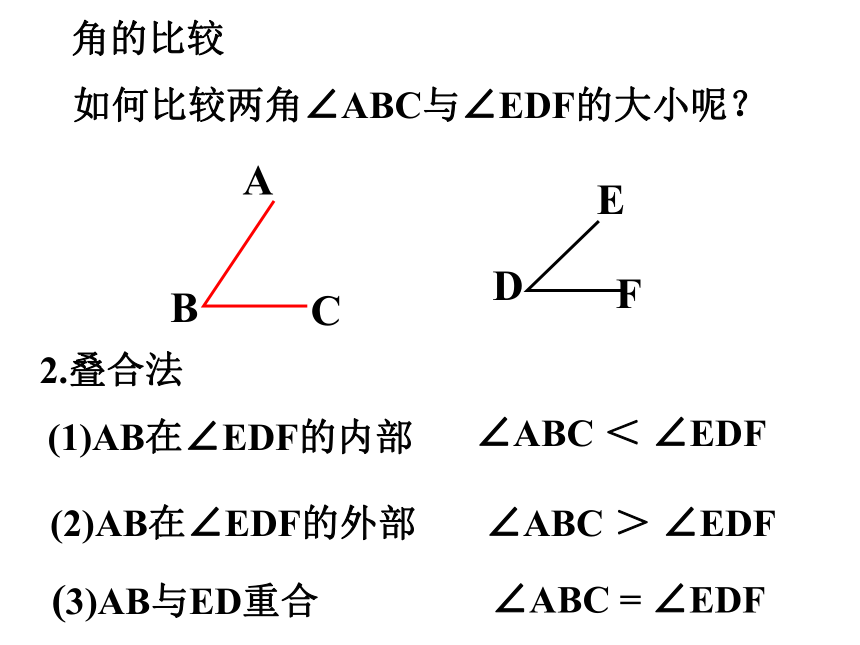
角的比较
如何比较两角∠ABC与∠EDF的大小呢?
2.叠合法
(1)AB在∠EDF的内部
(2)AB在∠EDF的外部
(3)AB与ED重合
∠ABC < ∠EDF
∠ABC > ∠EDF
∠ABC = ∠EDF
A
B
C
E
D
F
角的和、差
如图,∠AOC是∠AOB与∠BOC的和,
O
A
B
C
记作:∠AOC=∠AOB+
反之,∠AOB是∠AOC与 的差,
同理∠COB =∠AOC - .
记作:∠AOB =∠AOC - ,
∠COB
∠AOB
∠COB
∠BOC.
学习新知
例1 如图4-27,求解下列问题:
(1).比较∠AOC与∠BOC,
∠BOD与∠COD的大小;
(2).将∠AOC写成两个角的和
与两个角的差的形式.
O
A
B
C
D
(1) 由图可以看出:
∠AOC ∠BOC
解:
∠BOD ∠COD
(OB在∠AOC的内)
>
(OC在∠BOD的内)
>
例题解析
例1 如图4-27,求解下列问题:
(1).比较∠AOC与∠BOC,
∠BOD与∠COD的大小;
(2).将∠AOC写成两个角的和
与两个角的差的形式.
O
A
B
C
D
解:
(2)∠AOC =
∠AOD -
∠AOC =
∠AOB+
∠BOC
∠DOC
如图所示按要求完成下列填空
(1)∠EBA =∠EBC+ ;
(2)∠CBD =∠EBD- ;
=∠ABC- ;
(3)∠EBD+∠ABC-∠EBA = .
E
C
D
A
B
∠CBA
∠EBC
∠ABD
巩固新知
∠CBD
对折任意一角,(使角的两边互相重合),在角的内部过顶点沿折线画一条射线,这条射线把原来的角分成两个角,这两个角有什么样的数量关系呢?
A
C
O
B
图4-28
学习新知
在角的内部,以角的顶点为端点的一条射线把这个角分成两个相等的角,这条射线叫做这个角的平分线.
角的平分线
∴∠AOC=∠BOC,
∵OC是∠AOB的角平分线,
∠AOB=2∠AOC ,
A
C
O
B
图4-28
∠AOB,
∠AOC=
∠AOB=2∠BOC.
∠BOC=
∠AOB,
1
2
1
2
角的平分线符号语言.
1.如图所示按要求完成下列各题
(1) 若∠CBE=30°,∠ABC=90°,
你能求出哪些角的度数?
(2)在(1)条件下,在添加BD平分∠ABE,
你还能求出哪些角的度数?
E
C
D
A
B
30°
(1)能求出∠EBA度数,
∠EBA=120°.
(2)还能求出∠CBD,∠ABD,∠EBD度数,
∠CBD=∠ABD=45°,∠EBD=75°.
巩固新知
2.已知如图,OB是∠AOC的平分线,OD是
∠COE的平分线.
(1)∠AOB=40°,∠DOE=30°,那么∠BOD是
多少度?
(2)如果∠AOE=140°,∠COD=30°,那么
∠AOB是多少度?
E
B
A
C
D
O
2.已知如图,OB是∠AOC的平分线,OD是
∠COE的平分线.(1)∠AOB=40°∠DOE=30°,
那么∠BOD是多少度?
E
B
A
C
D
O
∵ OB是∠AOC的平分线,
∵ OD是 ∠COE的平分线.
解:(1)
∴∠AOB=∠BOC,
∴∠COD =∠DOE,
∴∠BOD = ∠BOC+∠DOC
∵ ∠AOB=40°,∠DOE=30°,
∴ ∠BOC=40°,∠DOC=30°,
=70°
2.已知如图,OB是∠AOC的平分线,OD是 ∠COE的平分线. (2)如果∠AOE=140°, ∠COD=30°,那么 ∠AOB是多少度?
E
B
A
C
D
O
∵ OB是∠AOC的平分线,
∵ OD是 ∠COE的平分线.
解:(2)
∴∠AOB= ∠AOC
∴∠COE =2∠COD,
∴∠AOC=∠AOE-∠EOC
∵ ∠COD=30°,
∴ ∠COE=60°,
=80°.
∵ ∠AOE=140°,
-
2
1
=40°.
=140°-60°
角的
比较
大小
比较
角的
和差
角平
分线
两重合一比较
>、 = 、 <
在内部、射线
两个相等的角
多个角的和
多个角的差
通过这节课学习,你有什么收获?
课堂小结
1. 在∠AOB的内部,做一条射线OC,则一定
存在( ).
A.∠AOC >∠BOC B.∠AOC <∠BOC
C.∠AOC = ∠BOC D.∠AOB >∠BOC
2. 如图,OC平分∠BOD, OD平分∠AOC,
下列等式不成立的是( ).
A.∠BOC=∠AOD
B.∠COD= ∠AOB
C.∠BOC= ∠AOC
D.∠AOB=3∠COD
A
B
C
D
O
1
2
1
2
巩固新知
D
B
3.如图所示:
∠BOC= + ,
= - ;
∠COD= - ,
= - .
4.将长方形纸条折成如图所示的
形状,BC为折痕,若∠ABD=70°,
则∠ABC的度数是 .
B
D
A
C
70°
A
B
C
D
O
∠BOD
∠COD
∠AOB
∠AOC
∠AOD
∠AOC
∠BOC
∠BOD
55°
今天作业
课本P150页第1、2、3 题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 七年级上册
4.5 角的比较与补(余)角(1)
课件说明
1.知道比较角的大小的两种方法;
教学目标
2.掌握角平分线的定义.
教学重点:
角平分线的定义及表示方法.
我们是如何比较线段的长短的?
A
B
C
D
1.度量法
2.叠合法
复习旧知
角的比较
如何比较两角∠ABC与∠EDF的大小呢?
1.度量法:
度数大的角就大,度数小的角就小.
A
B
C
E
D
F
学习新知
角的比较
如何比较两角∠ABC与∠EDF的大小呢?
A
B
C
E
D
F
2.叠合法
“两”重合“一”比较
学习新知
(1) AB在∠EDF的内部
∠ABC < ∠EDF
C
A
B
(F)
(D)
E
角的比较
(2) AB在∠EDF的外部
C
A
B
(F)
(D)
E
∠ABC > ∠EDF
角的比较
(3)AB与ED重合
(F)
C
B
E(A)
(D)
∠ABC = ∠EDF
角的比较
角的比较
如何比较两角∠ABC与∠EDF的大小呢?
2.叠合法
(1)AB在∠EDF的内部
(2)AB在∠EDF的外部
(3)AB与ED重合
∠ABC < ∠EDF
∠ABC > ∠EDF
∠ABC = ∠EDF
A
B
C
E
D
F
角的和、差
如图,∠AOC是∠AOB与∠BOC的和,
O
A
B
C
记作:∠AOC=∠AOB+
反之,∠AOB是∠AOC与 的差,
同理∠COB =∠AOC - .
记作:∠AOB =∠AOC - ,
∠COB
∠AOB
∠COB
∠BOC.
学习新知
例1 如图4-27,求解下列问题:
(1).比较∠AOC与∠BOC,
∠BOD与∠COD的大小;
(2).将∠AOC写成两个角的和
与两个角的差的形式.
O
A
B
C
D
(1) 由图可以看出:
∠AOC ∠BOC
解:
∠BOD ∠COD
(OB在∠AOC的内)
>
(OC在∠BOD的内)
>
例题解析
例1 如图4-27,求解下列问题:
(1).比较∠AOC与∠BOC,
∠BOD与∠COD的大小;
(2).将∠AOC写成两个角的和
与两个角的差的形式.
O
A
B
C
D
解:
(2)∠AOC =
∠AOD -
∠AOC =
∠AOB+
∠BOC
∠DOC
如图所示按要求完成下列填空
(1)∠EBA =∠EBC+ ;
(2)∠CBD =∠EBD- ;
=∠ABC- ;
(3)∠EBD+∠ABC-∠EBA = .
E
C
D
A
B
∠CBA
∠EBC
∠ABD
巩固新知
∠CBD
对折任意一角,(使角的两边互相重合),在角的内部过顶点沿折线画一条射线,这条射线把原来的角分成两个角,这两个角有什么样的数量关系呢?
A
C
O
B
图4-28
学习新知
在角的内部,以角的顶点为端点的一条射线把这个角分成两个相等的角,这条射线叫做这个角的平分线.
角的平分线
∴∠AOC=∠BOC,
∵OC是∠AOB的角平分线,
∠AOB=2∠AOC ,
A
C
O
B
图4-28
∠AOB,
∠AOC=
∠AOB=2∠BOC.
∠BOC=
∠AOB,
1
2
1
2
角的平分线符号语言.
1.如图所示按要求完成下列各题
(1) 若∠CBE=30°,∠ABC=90°,
你能求出哪些角的度数?
(2)在(1)条件下,在添加BD平分∠ABE,
你还能求出哪些角的度数?
E
C
D
A
B
30°
(1)能求出∠EBA度数,
∠EBA=120°.
(2)还能求出∠CBD,∠ABD,∠EBD度数,
∠CBD=∠ABD=45°,∠EBD=75°.
巩固新知
2.已知如图,OB是∠AOC的平分线,OD是
∠COE的平分线.
(1)∠AOB=40°,∠DOE=30°,那么∠BOD是
多少度?
(2)如果∠AOE=140°,∠COD=30°,那么
∠AOB是多少度?
E
B
A
C
D
O
2.已知如图,OB是∠AOC的平分线,OD是
∠COE的平分线.(1)∠AOB=40°∠DOE=30°,
那么∠BOD是多少度?
E
B
A
C
D
O
∵ OB是∠AOC的平分线,
∵ OD是 ∠COE的平分线.
解:(1)
∴∠AOB=∠BOC,
∴∠COD =∠DOE,
∴∠BOD = ∠BOC+∠DOC
∵ ∠AOB=40°,∠DOE=30°,
∴ ∠BOC=40°,∠DOC=30°,
=70°
2.已知如图,OB是∠AOC的平分线,OD是 ∠COE的平分线. (2)如果∠AOE=140°, ∠COD=30°,那么 ∠AOB是多少度?
E
B
A
C
D
O
∵ OB是∠AOC的平分线,
∵ OD是 ∠COE的平分线.
解:(2)
∴∠AOB= ∠AOC
∴∠COE =2∠COD,
∴∠AOC=∠AOE-∠EOC
∵ ∠COD=30°,
∴ ∠COE=60°,
=80°.
∵ ∠AOE=140°,
-
2
1
=40°.
=140°-60°
角的
比较
大小
比较
角的
和差
角平
分线
两重合一比较
>、 = 、 <
在内部、射线
两个相等的角
多个角的和
多个角的差
通过这节课学习,你有什么收获?
课堂小结
1. 在∠AOB的内部,做一条射线OC,则一定
存在( ).
A.∠AOC >∠BOC B.∠AOC <∠BOC
C.∠AOC = ∠BOC D.∠AOB >∠BOC
2. 如图,OC平分∠BOD, OD平分∠AOC,
下列等式不成立的是( ).
A.∠BOC=∠AOD
B.∠COD= ∠AOB
C.∠BOC= ∠AOC
D.∠AOB=3∠COD
A
B
C
D
O
1
2
1
2
巩固新知
D
B
3.如图所示:
∠BOC= + ,
= - ;
∠COD= - ,
= - .
4.将长方形纸条折成如图所示的
形状,BC为折痕,若∠ABD=70°,
则∠ABC的度数是 .
B
D
A
C
70°
A
B
C
D
O
∠BOD
∠COD
∠AOB
∠AOC
∠AOD
∠AOC
∠BOC
∠BOD
55°
今天作业
课本P150页第1、2、3 题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
