4.5 角的比较与补(余)角(2) 课件(共25张PPT)
文档属性
| 名称 | 4.5 角的比较与补(余)角(2) 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 936.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-05 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
沪科版 七年级上册
4.5 角的比较与补(余)角(2)
课件说明
1.理解余角,补角的概念;
掌握余角,补角的性质;
教学目标
2.会利用余角,补角的性质进行简单的运算.
教学重点:
利用余角,补角的性质进行简单的运算.
180°是什么样的角?
请同学们画一个平角∠AOB,
在内部过顶点任画一条射线OM,
你有什么发现?
平角
探究新知
O
A
B
M
总结:
射线OM把∠AOB分成∠AOM和∠BOM, 且∠AOM + ∠BOM =∠ = ° .
请同学们画一个平角∠AOB,在内部过顶点任画一条射线OM,你有什么发现?
AOB
180
如果两个角的和等于一个平角,那么
我们就称这两个角互为补角,简称互补.
2
图4-29
1
如图4-29,∠1+∠2=180°,
∠1叫做∠2的补角,
∠2也叫做∠1的补角,
∠1与∠2互补.
学习新知
90°是什么样的角?
请同学们画一个直角∠EDF,
并在内部过顶点任画一条射线ON.
你有什么发现?
直角
探究新知
E
D
F
N
发现:
射线DN把∠EDF分成 和 ,且 + = = °.
请同学们画一个直角∠EDF,并在内部过顶点任画一条射线ON.你有什么发现?
∠EDN
∠NDF
∠EDN
∠NDF
∠EDF
90
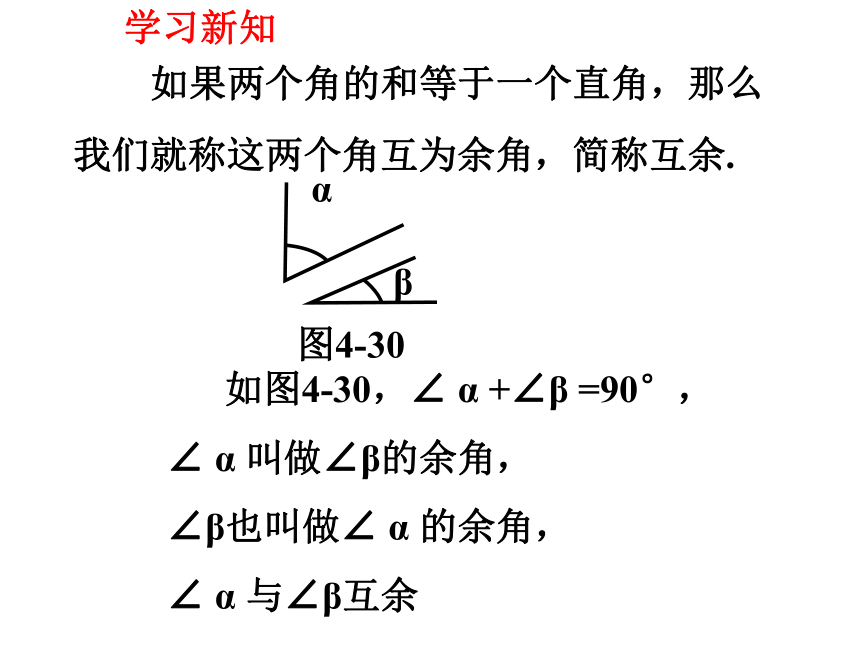
如果两个角的和等于一个直角,那么
我们就称这两个角互为余角,简称互余.
如图4-30,∠ α +∠β =90°,
∠ α 叫做∠β的余角,
∠β也叫做∠ α 的余角,
∠ α 与∠β互余
β
图4-30
α
学习新知
⑶ 也可用减法的形式呈现.
关于互补与互余
⑴ 角是成对出现;
⑵ 只是存在数量关系,与位置无关.
∠1与∠2互补,
∠α =90°-∠β
∠α 与∠β互补
∠1=180°-∠2
1.(1)∠1与∠2互补,则∠1 +∠2= °;
(2)∠1=90°- ∠2,则∠1与∠2 ;
(3) 60°的余角是 ° ,补角是 °;
(4) 若一个锐角的度数是 x,则它的余角是 °,
补角是 °;
(5)30°角的余角的补角是 °.
180
互余
30
120
(90-x)
(180-x)
120
巩固新知
2.已知:如图,点O为直线AB上一点,OC 是
∠AOB的平分线,OD在∠COB内.看图填空:
O
A
B
D
C
∠AOD的补角是 ,
∠COD的余角是 ,
∠BOD的补角是 ,
∠AOC的补角是 .
∠BOD
∠BOD
∠AOD
∠BOC
4.一个角的补角是它的3倍,这个角是 度.
45
3.已知∠ 1=27°43 ′ ,则∠1角的余角是 ;
∠1的补角是 .
62°17 ′
152°17 ′
2
1
3
同角的补角相等
如图,∠1与∠3都是∠2的补角,那么∠1与∠3相等吗?为什么
补角的性质
∴∠1+∠2=180°,
∵∠1 是∠2的补角,
∴ ∠1= 180°-∠ 2 。
∵∠3 是∠2的补角,
∴∠3+∠2=180°,
∴ ∠3= 180°-∠ 2 ,
∴ ∠1=∠3 .
答: ∠1与∠3相等 .
理由如下:
探究新知
2
1
3
4
等角的补角相等
∴∠1+∠2=180°,
∵∠1 与∠2互补,
∴ ∠2= 180°-∠ 1 。
∵∠3 与∠4互补,
∴∠3+∠4=180°,
∴ ∠4= 180°-∠ 3 。
∴ ∠2=∠4 .
∵∠1 =∠3,
答: ∠2与∠4相等 .
理由如下:
1
2
3
C
B
O
A
D
∠2和∠3都是∠1的余角,它们有什么关系?
同角的余角相等
余角的性质
∴∠1+∠2=90°,
∵∠2 是∠1的余角,
∴ ∠2= 90°-∠ 1 ,
∵∠3 是∠1的余角,
∴∠1+∠3=90°,
∴ ∠3= 90°-∠ 1 ,
∴ ∠2=∠3 .
答: ∠2与∠3相等 .
理由如下:
探究新知
1
3
2
4
等角的余角相等
∴∠1+∠2=90°,
∵∠1 与∠2互余,
∴ ∠1= 90°-∠ 2 。
∵∠3 与∠4互余,
∴∠3+∠4=90°,
∴ ∠3= 90°-∠ 4 。
∴ ∠1=∠3 .
∵∠2 =∠4,
答: ∠1与∠3相等 .
理由如下:
补角的性质:同角(等角)的补角相等。
余角的性质:同角(等角)的余角相等。
学习新知
1
2
3
C
B
O
A
D
1
3
2
4
2
1
3
2
1
3
4
1.若∠A+∠B=90°,
∠B+∠C=90°,
则∠A ∠C,
理由是 .
2.已知∠A与∠B互补,且∠A 比∠B大30°,
则∠A的大小是 .
巩固新知
=
同角的余角相等
105°
课堂小结
1.互余、互补是两角之间的数量关系,
只与他们的度数和有关,与位置无关.
2.互余、互补概念中的角是成对出现的.
3.角 α的余角是90° -α ,补角是180° -α
同一个锐角的补角比余角大
4.只有锐角才有余角.
5.同角的余角(补角)相等;
等角的余角(补角)相等。
巩固提高
1.如果∠α既有余角,也有补角,那么
∠α的取值范围是( ).
A. 0°<∠α< 90° B. ∠α=90°
C.90°<∠α<180° D. ∠α=180°
A
2.互为补角的两个角的比是3:2,则这两个角
是( ).
A.108°,72° B.95°,85°
C.100°,80° D.120°,60°
A
3.一个角等于它的补角的5倍,这个角的
补角的余角是( ).
A.30° B.60° C.45° D.150°
B
4.若∠α=57°28′,那么∠α的余角∠β = ,
∠α的补角∠γ = , ∠ γ-∠α= .
32°32′
122°32′
65°4′
5.一个角的补角比这个角余角的3倍小18°,
求这个角的余角的度数.
解:
(180°-x°)=3(90°-x°) - 18°
解得: x = 36
答:这个角的度数是54 °.
余角是(90°-x°) ,
则它的补角是(180°-x°),
根据题意得:
设这个角是 x °,
∴这个角的余角的度数
90°-36°=54°.
今天作业
课本P151页第5、6、7 题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 七年级上册
4.5 角的比较与补(余)角(2)
课件说明
1.理解余角,补角的概念;
掌握余角,补角的性质;
教学目标
2.会利用余角,补角的性质进行简单的运算.
教学重点:
利用余角,补角的性质进行简单的运算.
180°是什么样的角?
请同学们画一个平角∠AOB,
在内部过顶点任画一条射线OM,
你有什么发现?
平角
探究新知
O
A
B
M
总结:
射线OM把∠AOB分成∠AOM和∠BOM, 且∠AOM + ∠BOM =∠ = ° .
请同学们画一个平角∠AOB,在内部过顶点任画一条射线OM,你有什么发现?
AOB
180
如果两个角的和等于一个平角,那么
我们就称这两个角互为补角,简称互补.
2
图4-29
1
如图4-29,∠1+∠2=180°,
∠1叫做∠2的补角,
∠2也叫做∠1的补角,
∠1与∠2互补.
学习新知
90°是什么样的角?
请同学们画一个直角∠EDF,
并在内部过顶点任画一条射线ON.
你有什么发现?
直角
探究新知
E
D
F
N
发现:
射线DN把∠EDF分成 和 ,且 + = = °.
请同学们画一个直角∠EDF,并在内部过顶点任画一条射线ON.你有什么发现?
∠EDN
∠NDF
∠EDN
∠NDF
∠EDF
90
如果两个角的和等于一个直角,那么
我们就称这两个角互为余角,简称互余.
如图4-30,∠ α +∠β =90°,
∠ α 叫做∠β的余角,
∠β也叫做∠ α 的余角,
∠ α 与∠β互余
β
图4-30
α
学习新知
⑶ 也可用减法的形式呈现.
关于互补与互余
⑴ 角是成对出现;
⑵ 只是存在数量关系,与位置无关.
∠1与∠2互补,
∠α =90°-∠β
∠α 与∠β互补
∠1=180°-∠2
1.(1)∠1与∠2互补,则∠1 +∠2= °;
(2)∠1=90°- ∠2,则∠1与∠2 ;
(3) 60°的余角是 ° ,补角是 °;
(4) 若一个锐角的度数是 x,则它的余角是 °,
补角是 °;
(5)30°角的余角的补角是 °.
180
互余
30
120
(90-x)
(180-x)
120
巩固新知
2.已知:如图,点O为直线AB上一点,OC 是
∠AOB的平分线,OD在∠COB内.看图填空:
O
A
B
D
C
∠AOD的补角是 ,
∠COD的余角是 ,
∠BOD的补角是 ,
∠AOC的补角是 .
∠BOD
∠BOD
∠AOD
∠BOC
4.一个角的补角是它的3倍,这个角是 度.
45
3.已知∠ 1=27°43 ′ ,则∠1角的余角是 ;
∠1的补角是 .
62°17 ′
152°17 ′
2
1
3
同角的补角相等
如图,∠1与∠3都是∠2的补角,那么∠1与∠3相等吗?为什么
补角的性质
∴∠1+∠2=180°,
∵∠1 是∠2的补角,
∴ ∠1= 180°-∠ 2 。
∵∠3 是∠2的补角,
∴∠3+∠2=180°,
∴ ∠3= 180°-∠ 2 ,
∴ ∠1=∠3 .
答: ∠1与∠3相等 .
理由如下:
探究新知
2
1
3
4
等角的补角相等
∴∠1+∠2=180°,
∵∠1 与∠2互补,
∴ ∠2= 180°-∠ 1 。
∵∠3 与∠4互补,
∴∠3+∠4=180°,
∴ ∠4= 180°-∠ 3 。
∴ ∠2=∠4 .
∵∠1 =∠3,
答: ∠2与∠4相等 .
理由如下:
1
2
3
C
B
O
A
D
∠2和∠3都是∠1的余角,它们有什么关系?
同角的余角相等
余角的性质
∴∠1+∠2=90°,
∵∠2 是∠1的余角,
∴ ∠2= 90°-∠ 1 ,
∵∠3 是∠1的余角,
∴∠1+∠3=90°,
∴ ∠3= 90°-∠ 1 ,
∴ ∠2=∠3 .
答: ∠2与∠3相等 .
理由如下:
探究新知
1
3
2
4
等角的余角相等
∴∠1+∠2=90°,
∵∠1 与∠2互余,
∴ ∠1= 90°-∠ 2 。
∵∠3 与∠4互余,
∴∠3+∠4=90°,
∴ ∠3= 90°-∠ 4 。
∴ ∠1=∠3 .
∵∠2 =∠4,
答: ∠1与∠3相等 .
理由如下:
补角的性质:同角(等角)的补角相等。
余角的性质:同角(等角)的余角相等。
学习新知
1
2
3
C
B
O
A
D
1
3
2
4
2
1
3
2
1
3
4
1.若∠A+∠B=90°,
∠B+∠C=90°,
则∠A ∠C,
理由是 .
2.已知∠A与∠B互补,且∠A 比∠B大30°,
则∠A的大小是 .
巩固新知
=
同角的余角相等
105°
课堂小结
1.互余、互补是两角之间的数量关系,
只与他们的度数和有关,与位置无关.
2.互余、互补概念中的角是成对出现的.
3.角 α的余角是90° -α ,补角是180° -α
同一个锐角的补角比余角大
4.只有锐角才有余角.
5.同角的余角(补角)相等;
等角的余角(补角)相等。
巩固提高
1.如果∠α既有余角,也有补角,那么
∠α的取值范围是( ).
A. 0°<∠α< 90° B. ∠α=90°
C.90°<∠α<180° D. ∠α=180°
A
2.互为补角的两个角的比是3:2,则这两个角
是( ).
A.108°,72° B.95°,85°
C.100°,80° D.120°,60°
A
3.一个角等于它的补角的5倍,这个角的
补角的余角是( ).
A.30° B.60° C.45° D.150°
B
4.若∠α=57°28′,那么∠α的余角∠β = ,
∠α的补角∠γ = , ∠ γ-∠α= .
32°32′
122°32′
65°4′
5.一个角的补角比这个角余角的3倍小18°,
求这个角的余角的度数.
解:
(180°-x°)=3(90°-x°) - 18°
解得: x = 36
答:这个角的度数是54 °.
余角是(90°-x°) ,
则它的补角是(180°-x°),
根据题意得:
设这个角是 x °,
∴这个角的余角的度数
90°-36°=54°.
今天作业
课本P151页第5、6、7 题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
