人教B版高中数学选择性必修第一册1.2.3 《直线与平面的夹角》名师 课件(共42张PPT)
文档属性
| 名称 | 人教B版高中数学选择性必修第一册1.2.3 《直线与平面的夹角》名师 课件(共42张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-05 00:00:00 | ||
图片预览










文档简介
(共42张PPT)
复习引入
一、平面的法向量
定义:如果是空间中的一个平面,是空间中的一个非零向量,且表示的有向线段所在的直线与平面垂直,则称为平面的一个法向量.此时,也称与平面垂直,记作⊥.
二、三垂线定理及其逆定理
三垂线定理:如果平面内的一条直线与平面的一条斜线在该平面内的射影垂直,则它也和这条斜线垂直
三垂线定理的逆定理:如果平面内的一条直线和这个平面的一条斜线垂直,则它也和这条斜线在该平面内的射影垂直
人教B版同步教材名师课件
直线与平面的夹角
学习目标
学 习 目 标 核心素养
理解直线与平面所成的角的概念 数学抽象
了解最小角定理及其应用 逻辑推理
会用向量方法求直线与平面所成的角 数学运算
学习目标
1.理解斜线和平面所成的角的定义,体会夹角定义的唯一性、合理性.
2.会求直线与平面的夹角.(重点、难点)
探究新知
一、直线与平面的夹角
同学们,我们都掷过铅球,那么是把铅球水平推出还是把它沿一定的角度向上推出时,才能掷得相对较远些呢 我们这里所说的角度,又是指的什么呢
日常生活中,很多场景中都有直线与平面成一定角度的形象.
例如,如图所示,握笔写字时,如果把笔抽象成直线,把纸抽象成平面,则直线与平面成一定角度;
如图所示,地球仪的地轴(即旋转轴)与赤道所在的平面垂直,并且与水平桌面成一定角度.那么,怎样来刻画直线与平面所成的角呢
探究新知
探究新知
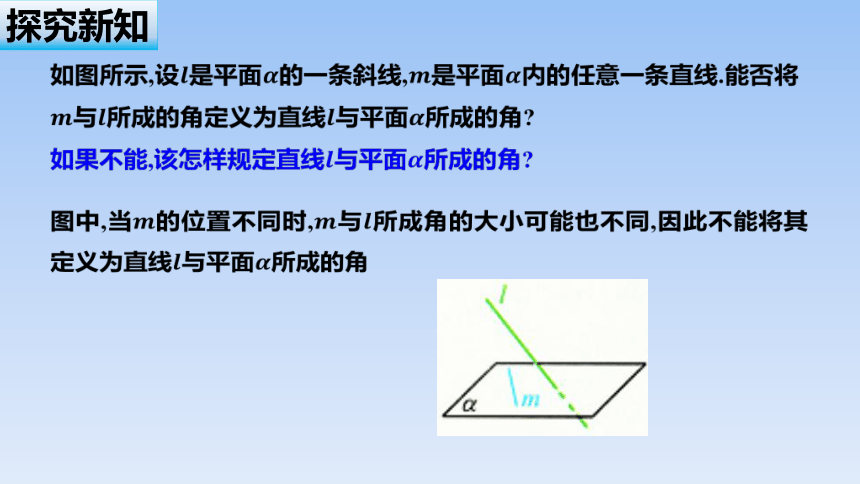
如图所示,设是平面的一条斜线,是平面内的任意一条直线.能否将与所成的角定义为直线与平面所成的角
如果不能,该怎样规定直线与平面所成的角
图中,当的位置不同时,与所成角的大小可能也不同,因此不能将其定义为直线与平面所成的角
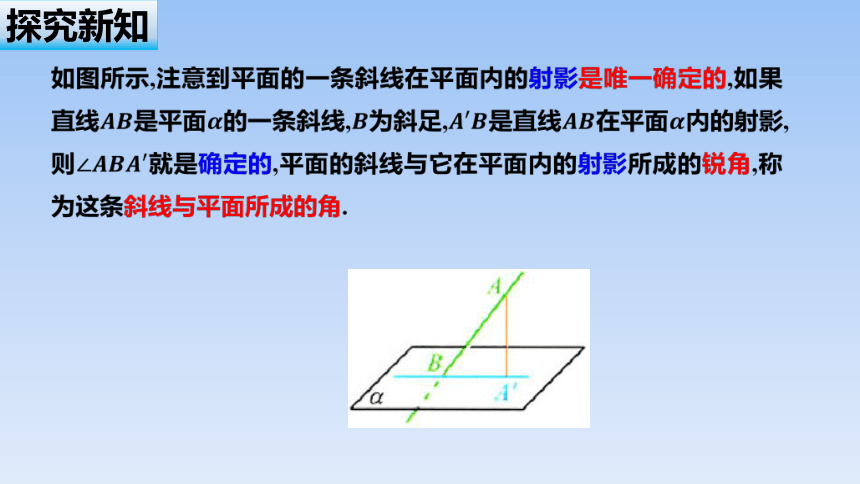
如图所示,注意到平面的一条斜线在平面内的射影是唯一确定的,如果直线是平面的一条斜线,为斜足,是直线在平面内的射影,则就是确定的,平面的斜线与它在平面内的射影所成的锐角,称为这条斜线与平面所成的角.
探究新知
探究新知
(1)范围:
①如果一条直线与一个平面垂直,则称这条直线与这个平面所成的角为;
②如果一条直线与一个平面平行,或直线在平面内,则称这条直线与这个平面所成的角为
(2)平面的斜线与它在平面内的射影所成的锐角,称为这条斜线与平面所成的角.
注意:引进了平面的斜线与平面所成的角后,空间中任意一条直线与任意个平面所成的角的大小都是确定的,直线与平面所成的角也称为它们的夹角.
1.平面的一条斜线和这个平面所成的角的大小的范围是( )
A. B. C. D.
变式训练
解析:由斜线和平面所成的角定义知选D.
2.平面的一条斜线段长是它在平面内射影长的2倍,则斜线与平面所成角的大小为( )
A. B. C. D.
解析:由题意知:设线面角的大小为,所以,所以.答案:
3.已知直线的一个方向向量与平面的一个法向量的夹角为,则直线与平面的夹角大小为( )
A. B. C. D.以上均错
变式训练
解析:因为直线与平面的夹角的范围是,所以直线与平面的夹角为答案:B
探究新知
如图所示,设是平面的一条斜线段,为斜足,为在平面内的射影,而是平面内的一条射线,⊥,记
,,
(1)从直观上判断与的大小关系;
(2)说明⊥是否成立,探究, ,三者之间的等量关系.
性质:
①平面的斜线与平面所成的角,是斜线和这个平面内所有直线所成角中最小的角(最小角定理).
探究新知
证明:
图中,因为⊥,所以,都是直角三角形,而且是在平面内的射影.因此,根据⊥与三垂线定理可知⊥,所以也是直角三角形.
如果设,则在中,= =cos ,
因此在中cos
另一方面,在中,有
因此
因为,所以由上式可知≤ ,因为和都是锐角,所以可得≤.
这就是说,平面的斜线与平面所成的角,是斜线和这个平面内所有直线所成角中最小的角.
探究新知
典例讲解
例1.如图所示,已知在平面内,过该角的顶点引平面的斜线,且使,求证:斜线在平面内的射影平分.
证明:设点在平面内的射影为点,则为在平面内的射影.
根据前面的结论有
,由=可得
.
因此,即平分.
变式训练
4.若在平面内,斜线与平面所成的角为,,⊥平面,垂足为,,那么有( )
A. B.
C. D.
解析:根据最小角定理可知直线和平面内所有直线所成角中最小的角为直线与平面的夹角.答案:
解析:利用公式求解.要明确公式中的,,分别代表哪些角.答案A
5.已知一条直线与平面的夹角大小为,则它和这个平面内所有直线所成角中最小的角大小为( )
A. B. C. D.
变式训练
变式训练
6.已知正四棱锥,在侧面中,,求直线与平面所成角的大小.
解析:如图
∵四棱锥是正四棱锥,
∴顶点在底面正方形的射影是中心,
∴是在平面内的射影,且平分.
由三余弦公式,得.
又∵,,∴
解得,即,
∴直线与平面所成角的大小为.
变式训练
探究新知
过平面外同点作两条斜线
(1)若斜线段长相等,那么两者的射影长有什么关系 两斜线与平面所成的角有什么关系
(2)若射影长相等,那么两斜线段长有什么关系 两斜线与平面所成的角有什么关系
(3)若两斜线与平面所成的角相等,那么两斜线段长有什么关系 两射影长有什么关系
探究新知
如图所示,是平面外一点,在平面内的射影为.过作平面的斜线段,,且, 均为斜足,设, 与平面所成角分别为,.试判断=是=的什么条件 =是=的什么条件
因为,所以与都是直角三角形,
从而
再根据,都是锐角,可知=是=的充要条件;
类似地,因为==,
所以=也是=的充要条件.
经过平面外同一点所作的平面的多条斜线中,斜线段长、射影长及斜线与平面所成的角,只要有一个相等则另外两个也对应相等
探究新知
探究新知
二、用空间向量求直线与平面的夹角
(1)你能根据定义概括一下求直线与平面的夹角的一般步骤吗
(2)通过前面的学习,我们可以借助向量来研究异面直线所成的角,那么你能借助直线的方向向量和平面的法向量来研究直线与平面所成的角吗
如果是直线的一个方向向量,是平面的一个法向量,设直线与平面所成角的大小为,通过作图讨论与的关系.
如图所示,可以看出或θ=
特别地,,
探究新知
典例讲解
例2.已知是正方体,求与平面所成角的大小.
解析:(方法一)如图,以为原点,,,的方向分别为轴、轴、轴正方向,正方体的棱长为单位长度,建立如图所示的空间直角坐标系.
则,,,
所以,, .
设平面的一个法向量为,则
取,可得.又因为
所以,从而可知与平面所成角的大小为.
典例讲解
典例讲解
(方法二)设的中点为,连接,,如图所示.
因为是正方形,所以⊥.
又因为⊥,且面,所以⊥.
再根据可知⊥面.
因此,在面内的射影为,所以就是与平面所成角.
因为正方体中有=,所以在中,,又因为是一个锐角,所以
,即与平面所成角的大小为.
典例讲解
变式训练
7.在正四面体中,为棱中点,连接,求和平面所成角的正弦值.
解析:如图,过,分别作⊥平面,⊥平面,,为垂足
∴⊥2且2,,确定平面.
连接,则为与平面所成的角.
∵,∴.
∵是正三角形,
∴为的中心,并且延长交于,则为的中点.
设正四面体棱长为,可求得,,,
∴,∴.
在中,.
变式训练
变式训练
8.如图,四棱锥中,是正三角形,四边形是菱形,点是的中点.
(1)求证:∥平面
(2)若平面⊥平面,,求直线与平面所成角的正弦值.
解析:
(1)证明:如图,连接交于点,再连接.
因为四边形是菱形,所以点是的中点.
又因为点是的中点,所以是的中位线,所以∥.
又因为平面,平面,所以∥平面.
(2)因为四边形是菱形,,所以.
又,所以为正三角形.取的中点,连接,,则⊥.
因为平面⊥平面,平面∩平面,所以⊥平面.
又因为为正三角形,所以⊥,则可以为坐标原点建立空间直角坐标系,如下图所示
变式训练
变式训练
设(),则,,,
所以.
设平面的一个法向量为,则
取,则, ,所以,
设直线与平面所成角为,
则.
素养提炼
利用定义法求线面角找射影的方法
定义法是指将求斜线与平面的夹角转化为求斜线与其在平面内射影的夹角,此种方法的关键是确定斜线在平面内的射影.
找射影有以下两种方法:
(1)斜线上任一点在平面内的射影,必在斜线在平面内的射影上,故找到斜线上任一点在平面内的射影,连接斜足和垂足即得;
(2)利用已知垂直关系得出线面垂直,连接斜足和垂足即得.
利用向量求直线与平面所成角的基本步骤:
(1)建立空间直角坐标系;
(2)求直线的一个方向向量
(3)求平面的一个法向量;
(4)计算:设线面角为,则.
素养提炼
当堂练习
1.下列三个命题中为真命题的个数是( )
(1)直线与平面的夹角不是锐角就是直角;
(2)斜线和它在平面内的射影所成的角是锐角;
(3)直线与平面的夹角的范围是
A.0 B.1 C.2 D.3
解析:(1)不正确,夹角的度数还可以是零度;其他两个命题均为真命题.答案:C
当堂练习
2.已知向量,分别是直线和平面的方向向量、法向量,若,则直线与平面所成的角为( )
A. B. C. D.
解析:由,得,∴直线与平面所成的角的大小为.答案:A
当堂练习
3.设直线与平面相交,且的一个方向向量为,的一个法向量为,若,则与所成的角为( )
解析:线面角的大小范围是,故与所成的角大小为.
答案:C
当堂练习
4.如图所示,点是所在平面外的一点,若,,与平面所成的角均相等,则点在平面上的射影是的( )
A.内心 B.外心 C.重心 D.垂心
解析:由于,,与平面所成的角均相等,所以这三条由点出发的平面的斜线段相等,故它们在平面内的射影,,也都相等,故点是的外心.答案:B
当堂练习
5.正四棱锥的侧棱长与底面边长都是,则侧棱与底面所成角的大小为__________.
解析:如图,正四棱锥中,点在平面的
射影为正方形的中心,则即为侧棱与
底面所成的角.在中,,,∴,∴侧棱与底面所成的角的大小为.答案:
归纳小结
直线与平面的夹角
直线与平面所成角
最小角定理
直线与平面所成角的求法
概念
范围
定义法
向量法
作 业
教材P46页练习第1,2题
P47页练习第1,2,3题
复习引入
一、平面的法向量
定义:如果是空间中的一个平面,是空间中的一个非零向量,且表示的有向线段所在的直线与平面垂直,则称为平面的一个法向量.此时,也称与平面垂直,记作⊥.
二、三垂线定理及其逆定理
三垂线定理:如果平面内的一条直线与平面的一条斜线在该平面内的射影垂直,则它也和这条斜线垂直
三垂线定理的逆定理:如果平面内的一条直线和这个平面的一条斜线垂直,则它也和这条斜线在该平面内的射影垂直
人教B版同步教材名师课件
直线与平面的夹角
学习目标
学 习 目 标 核心素养
理解直线与平面所成的角的概念 数学抽象
了解最小角定理及其应用 逻辑推理
会用向量方法求直线与平面所成的角 数学运算
学习目标
1.理解斜线和平面所成的角的定义,体会夹角定义的唯一性、合理性.
2.会求直线与平面的夹角.(重点、难点)
探究新知
一、直线与平面的夹角
同学们,我们都掷过铅球,那么是把铅球水平推出还是把它沿一定的角度向上推出时,才能掷得相对较远些呢 我们这里所说的角度,又是指的什么呢
日常生活中,很多场景中都有直线与平面成一定角度的形象.
例如,如图所示,握笔写字时,如果把笔抽象成直线,把纸抽象成平面,则直线与平面成一定角度;
如图所示,地球仪的地轴(即旋转轴)与赤道所在的平面垂直,并且与水平桌面成一定角度.那么,怎样来刻画直线与平面所成的角呢
探究新知
探究新知
如图所示,设是平面的一条斜线,是平面内的任意一条直线.能否将与所成的角定义为直线与平面所成的角
如果不能,该怎样规定直线与平面所成的角
图中,当的位置不同时,与所成角的大小可能也不同,因此不能将其定义为直线与平面所成的角
如图所示,注意到平面的一条斜线在平面内的射影是唯一确定的,如果直线是平面的一条斜线,为斜足,是直线在平面内的射影,则就是确定的,平面的斜线与它在平面内的射影所成的锐角,称为这条斜线与平面所成的角.
探究新知
探究新知
(1)范围:
①如果一条直线与一个平面垂直,则称这条直线与这个平面所成的角为;
②如果一条直线与一个平面平行,或直线在平面内,则称这条直线与这个平面所成的角为
(2)平面的斜线与它在平面内的射影所成的锐角,称为这条斜线与平面所成的角.
注意:引进了平面的斜线与平面所成的角后,空间中任意一条直线与任意个平面所成的角的大小都是确定的,直线与平面所成的角也称为它们的夹角.
1.平面的一条斜线和这个平面所成的角的大小的范围是( )
A. B. C. D.
变式训练
解析:由斜线和平面所成的角定义知选D.
2.平面的一条斜线段长是它在平面内射影长的2倍,则斜线与平面所成角的大小为( )
A. B. C. D.
解析:由题意知:设线面角的大小为,所以,所以.答案:
3.已知直线的一个方向向量与平面的一个法向量的夹角为,则直线与平面的夹角大小为( )
A. B. C. D.以上均错
变式训练
解析:因为直线与平面的夹角的范围是,所以直线与平面的夹角为答案:B
探究新知
如图所示,设是平面的一条斜线段,为斜足,为在平面内的射影,而是平面内的一条射线,⊥,记
,,
(1)从直观上判断与的大小关系;
(2)说明⊥是否成立,探究, ,三者之间的等量关系.
性质:
①平面的斜线与平面所成的角,是斜线和这个平面内所有直线所成角中最小的角(最小角定理).
探究新知
证明:
图中,因为⊥,所以,都是直角三角形,而且是在平面内的射影.因此,根据⊥与三垂线定理可知⊥,所以也是直角三角形.
如果设,则在中,= =cos ,
因此在中cos
另一方面,在中,有
因此
因为,所以由上式可知≤ ,因为和都是锐角,所以可得≤.
这就是说,平面的斜线与平面所成的角,是斜线和这个平面内所有直线所成角中最小的角.
探究新知
典例讲解
例1.如图所示,已知在平面内,过该角的顶点引平面的斜线,且使,求证:斜线在平面内的射影平分.
证明:设点在平面内的射影为点,则为在平面内的射影.
根据前面的结论有
,由=可得
.
因此,即平分.
变式训练
4.若在平面内,斜线与平面所成的角为,,⊥平面,垂足为,,那么有( )
A. B.
C. D.
解析:根据最小角定理可知直线和平面内所有直线所成角中最小的角为直线与平面的夹角.答案:
解析:利用公式求解.要明确公式中的,,分别代表哪些角.答案A
5.已知一条直线与平面的夹角大小为,则它和这个平面内所有直线所成角中最小的角大小为( )
A. B. C. D.
变式训练
变式训练
6.已知正四棱锥,在侧面中,,求直线与平面所成角的大小.
解析:如图
∵四棱锥是正四棱锥,
∴顶点在底面正方形的射影是中心,
∴是在平面内的射影,且平分.
由三余弦公式,得.
又∵,,∴
解得,即,
∴直线与平面所成角的大小为.
变式训练
探究新知
过平面外同点作两条斜线
(1)若斜线段长相等,那么两者的射影长有什么关系 两斜线与平面所成的角有什么关系
(2)若射影长相等,那么两斜线段长有什么关系 两斜线与平面所成的角有什么关系
(3)若两斜线与平面所成的角相等,那么两斜线段长有什么关系 两射影长有什么关系
探究新知
如图所示,是平面外一点,在平面内的射影为.过作平面的斜线段,,且, 均为斜足,设, 与平面所成角分别为,.试判断=是=的什么条件 =是=的什么条件
因为,所以与都是直角三角形,
从而
再根据,都是锐角,可知=是=的充要条件;
类似地,因为==,
所以=也是=的充要条件.
经过平面外同一点所作的平面的多条斜线中,斜线段长、射影长及斜线与平面所成的角,只要有一个相等则另外两个也对应相等
探究新知
探究新知
二、用空间向量求直线与平面的夹角
(1)你能根据定义概括一下求直线与平面的夹角的一般步骤吗
(2)通过前面的学习,我们可以借助向量来研究异面直线所成的角,那么你能借助直线的方向向量和平面的法向量来研究直线与平面所成的角吗
如果是直线的一个方向向量,是平面的一个法向量,设直线与平面所成角的大小为,通过作图讨论与的关系.
如图所示,可以看出或θ=
特别地,,
探究新知
典例讲解
例2.已知是正方体,求与平面所成角的大小.
解析:(方法一)如图,以为原点,,,的方向分别为轴、轴、轴正方向,正方体的棱长为单位长度,建立如图所示的空间直角坐标系.
则,,,
所以,, .
设平面的一个法向量为,则
取,可得.又因为
所以,从而可知与平面所成角的大小为.
典例讲解
典例讲解
(方法二)设的中点为,连接,,如图所示.
因为是正方形,所以⊥.
又因为⊥,且面,所以⊥.
再根据可知⊥面.
因此,在面内的射影为,所以就是与平面所成角.
因为正方体中有=,所以在中,,又因为是一个锐角,所以
,即与平面所成角的大小为.
典例讲解
变式训练
7.在正四面体中,为棱中点,连接,求和平面所成角的正弦值.
解析:如图,过,分别作⊥平面,⊥平面,,为垂足
∴⊥2且2,,确定平面.
连接,则为与平面所成的角.
∵,∴.
∵是正三角形,
∴为的中心,并且延长交于,则为的中点.
设正四面体棱长为,可求得,,,
∴,∴.
在中,.
变式训练
变式训练
8.如图,四棱锥中,是正三角形,四边形是菱形,点是的中点.
(1)求证:∥平面
(2)若平面⊥平面,,求直线与平面所成角的正弦值.
解析:
(1)证明:如图,连接交于点,再连接.
因为四边形是菱形,所以点是的中点.
又因为点是的中点,所以是的中位线,所以∥.
又因为平面,平面,所以∥平面.
(2)因为四边形是菱形,,所以.
又,所以为正三角形.取的中点,连接,,则⊥.
因为平面⊥平面,平面∩平面,所以⊥平面.
又因为为正三角形,所以⊥,则可以为坐标原点建立空间直角坐标系,如下图所示
变式训练
变式训练
设(),则,,,
所以.
设平面的一个法向量为,则
取,则, ,所以,
设直线与平面所成角为,
则.
素养提炼
利用定义法求线面角找射影的方法
定义法是指将求斜线与平面的夹角转化为求斜线与其在平面内射影的夹角,此种方法的关键是确定斜线在平面内的射影.
找射影有以下两种方法:
(1)斜线上任一点在平面内的射影,必在斜线在平面内的射影上,故找到斜线上任一点在平面内的射影,连接斜足和垂足即得;
(2)利用已知垂直关系得出线面垂直,连接斜足和垂足即得.
利用向量求直线与平面所成角的基本步骤:
(1)建立空间直角坐标系;
(2)求直线的一个方向向量
(3)求平面的一个法向量;
(4)计算:设线面角为,则.
素养提炼
当堂练习
1.下列三个命题中为真命题的个数是( )
(1)直线与平面的夹角不是锐角就是直角;
(2)斜线和它在平面内的射影所成的角是锐角;
(3)直线与平面的夹角的范围是
A.0 B.1 C.2 D.3
解析:(1)不正确,夹角的度数还可以是零度;其他两个命题均为真命题.答案:C
当堂练习
2.已知向量,分别是直线和平面的方向向量、法向量,若,则直线与平面所成的角为( )
A. B. C. D.
解析:由,得,∴直线与平面所成的角的大小为.答案:A
当堂练习
3.设直线与平面相交,且的一个方向向量为,的一个法向量为,若,则与所成的角为( )
解析:线面角的大小范围是,故与所成的角大小为.
答案:C
当堂练习
4.如图所示,点是所在平面外的一点,若,,与平面所成的角均相等,则点在平面上的射影是的( )
A.内心 B.外心 C.重心 D.垂心
解析:由于,,与平面所成的角均相等,所以这三条由点出发的平面的斜线段相等,故它们在平面内的射影,,也都相等,故点是的外心.答案:B
当堂练习
5.正四棱锥的侧棱长与底面边长都是,则侧棱与底面所成角的大小为__________.
解析:如图,正四棱锥中,点在平面的
射影为正方形的中心,则即为侧棱与
底面所成的角.在中,,,∴,∴侧棱与底面所成的角的大小为.答案:
归纳小结
直线与平面的夹角
直线与平面所成角
最小角定理
直线与平面所成角的求法
概念
范围
定义法
向量法
作 业
教材P46页练习第1,2题
P47页练习第1,2,3题
