人教B版高中数学选择性必修第一册1.2.4《二面角》名师课件(共45张PPT)
文档属性
| 名称 | 人教B版高中数学选择性必修第一册1.2.4《二面角》名师课件(共45张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-05 10:31:30 | ||
图片预览






文档简介
(共45张PPT)
复习引入
直线与平面的夹角
直线与平面所成角
最小角定理
直线与平面所成角的求法
概念
范围
定义法
向量法
人教B版同步教材名师课件
二面角
学习目标
学 习 目 标 核心素养
理解二面角及其平面角的概念 数学抽象
会利用定义法求二面角的大小 逻辑推理和直观想象
会用向量法求二面角的大小 直观想象和数学运算
学习目标
重点:理解二面角及二面角的平面角的定义,会求二面角的大小.
难点:求二面角大小的基本方法及步骤.
我们知道,地球绕太阳公转的轨道平面称为“黄道面’’.黄道面与地球赤道面交角(二面角的平面角)约为23°26′,它与天球相交的大圆为“黄道’’.
探究新知
黄道及其附近的南北共宽18°以内的区域为黄道带.黄道带内有十二个星座,称 为“黄道十二宫’’,从春分(节气)点起,每30°便是一宫,并冠以星座名,如白羊座、金牛座、双子座等等这便是星座的由来,今天我们研究的问题便是二面角的平面角问题.
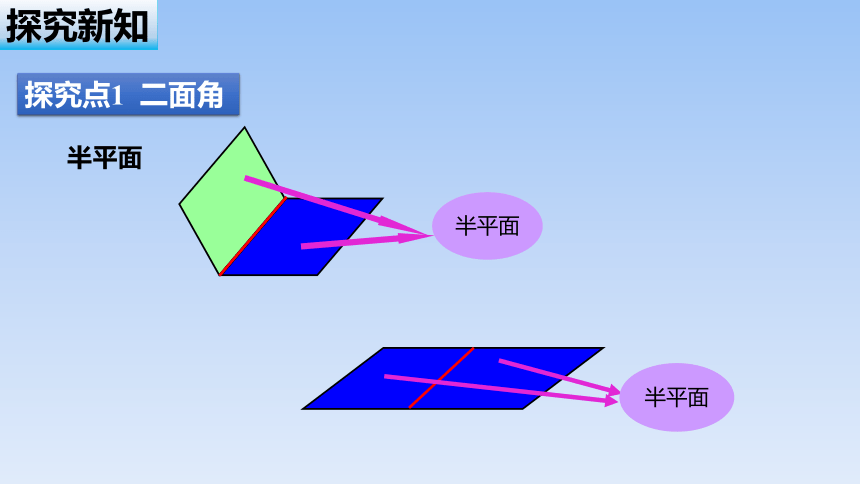
半平面
半平面
半平面
探究点1 二面角
探究新知
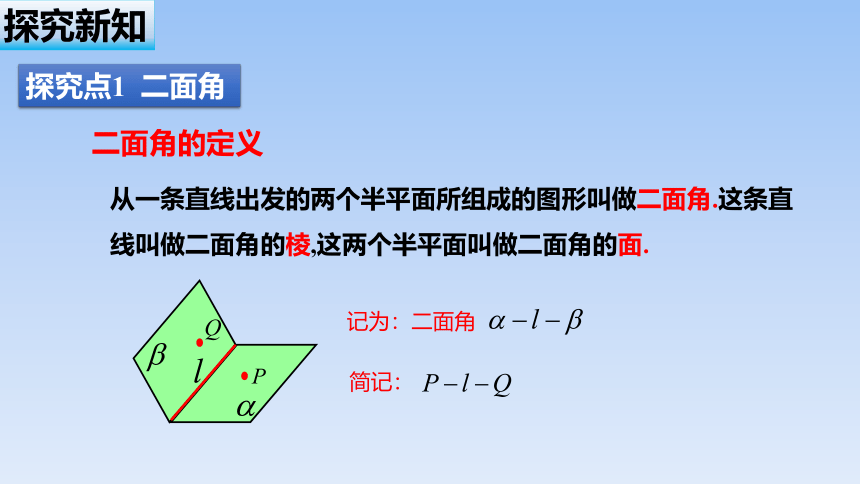
从一条直线出发的两个半平面所组成的图形叫做二面角.这条直线叫做二面角的棱,这两个半平面叫做二面角的面.
记为:二面角
简记:
二面角的定义
探究新知
探究点1 二面角
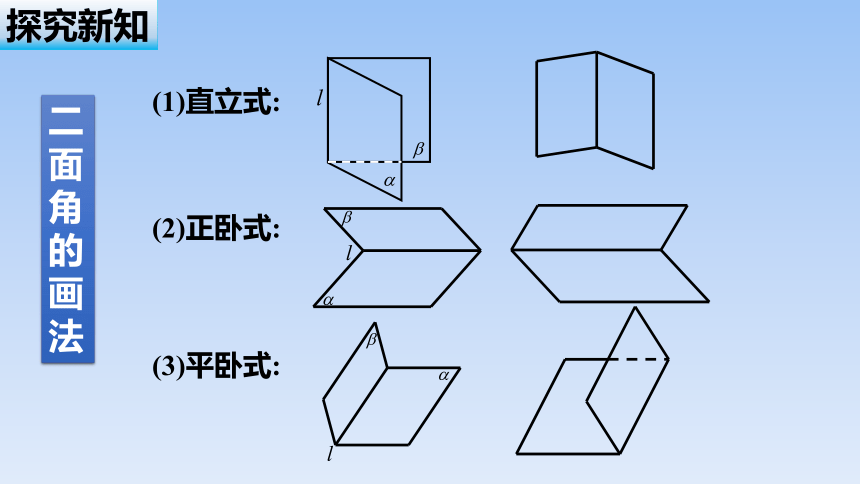
(1)直立式:
(2)正卧式:
(3)平卧式:
二面角的画法
探究新知
β
2.二面角的取值范围:
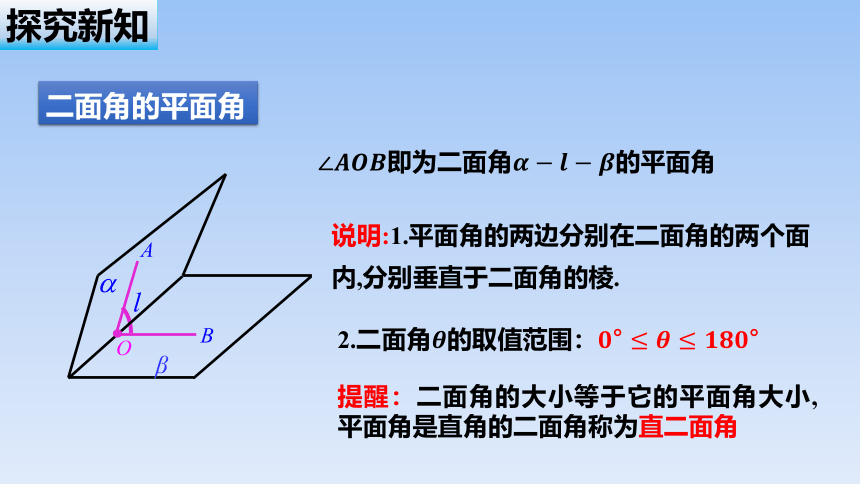
二面角的平面角
说明:1.平面角的两边分别在二面角的两个面内,分别垂直于二面角的棱.
探究新知
即为二面角的平面角
提醒:二面角的大小等于它的平面角大小,平面角是直角的二面角称为直二面角
β
平面角的大小与棱上点的选取无关.
探究新知
∠的大小与点在上的位置有关系吗 为什么
D
端点
中点
寻找二面角的一般规律
探究新知
中点
E
G
F
探究新知
寻找二面角的一般规律
例1.判断正误.
(1)两个相交平面组成的图形叫做二面角 ( )
(2)异面直线分别和一个二面角的两个半平面垂直,则所成的角与这个
二面角的平面角相等或互补( )
(3)二面角的平面角是从棱上一点出发,分别在两个半平面内作射线所成角
的最小角( )
(4)二面角的大小与其平面角的顶点在棱上的位置没有关系( )
×
×
√
√
典例讲解
典例讲解
例2.如图所示,在正方体中,求二面角的大小.
解:连接和.
由已知有面
所以,
因此即为二面角的平面角
由于是等腰直角三角形,因此,
所以二面角的大小为45°
方法一:(定义法)在二面角的棱上找一个特殊点,在两个半平面内分别作垂直于棱的射线.如图所示,为二面角的平面角.
方法二:(三垂线定理法)当二面角是一个锐角时,过其中一个半平面内一点,作另一个半平面的垂线段,过(或)作棱的垂线(或),连接(或)即可.如果二面角的大小为, 则.
探究新知
思考:如何找二面角的平面角?
典例讲解
例3.如图所示,已知二面角的棱上有 ,两个点, , , , 若 ,,,求二面角的大小.
解:如图所示,在平面内过作的平行线,且使得,连接.
因为四边形是一个矩形,是二面角的一个平面角,且面,所以面,从而.
典例讲解
例3.如图所示,已知二面角的棱上有 ,两个点, , , , 若 ,,,求二面角的大小.
在中,由余弦定理可知
因此
即所求二面角的大小为.
典例讲解
例4.如图所示三棱锥面中,面面,,且,求二面角的大小.
解: 设别为的中点,连接.如图所示.
因为,所以,又因为面面,
所以面,因此在平面内的射影为.
又因为为的中位线,,所以,
从而由三垂线定理可知,
因此为二面角的一个平面角.
典例讲解
例4.如图所示三棱锥面中,面面,,且,求二面角的大小.
由且可知 ,又因为.
而且,从而可知,
即所求二面角的大小为.
定义法求二面角的一般步骤
方法归纳
简称为“一作二证三求’’
三垂线定理法求二面角的一般步骤
方法归纳
在其中一个面内找一个特殊点作另一个面的垂线
过垂足作棱的垂线(或过这个特殊点作棱的垂线)
连接特殊点与垂足(或两个垂足),根据三垂线定理或其逆定理)得二面角的平面角
变式训练
1.如图,在正方体中,求二面角的正切值
解:取的中点,连接,
由题意知,又,为的中点,
所以,
所以即是二面角的平面角,
因为平面,平面,
所以⊥.
变式训练
1.如图,在正方体中,求二面角的正切值
设正方体的棱长为,则,
在中,.
所以二面角的正切值为.
2.如果二面角α -l- β的平面角是锐角,点P到α、β和棱l的距离分别为2、4和4,求其二面角的大小.
解:①当点P在二面角α- l -β的内部时,如图①.
因为PA⊥α,所以PA⊥l.
因为AC⊥l,所以l⊥平面PAC.同理,l⊥平面PBC,
而平面PAC∩平面PBC=PC,
所以平面PAC与平面PBC应重合.
即A、C、B、P在同一平面内.
所以∠ACB是二面角α- l -β的平面角.
变式训练
2.如果二面角α -l- β的平面角是锐角,点P到α、β和棱l的距离分别为2、4和4,求其二面角的大小.
在Rt△APC中, .所以.
在Rt△BPC中,.所以.
所以.
②当点P在二面角α -l- β的外部时,如图②.
同理可得.
综上,知所求二面角的大小为或.
变式训练
3.如图所示,在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.
(1)证明:AB⊥平面VAD;
(2)求面VAD与面VDB夹角的正切值.
变式训练
解:(1)证明:
∵平面VAD⊥平面ABCD,交线为AD.
AB 平面ABCD,AB⊥AD.
∴AB⊥平面VAD.
(2)如图,取VD的中点E,连接AE,BE.
∵△VAD是正三角形,∴AE⊥VD,.
∵AB⊥平面VAD,∴AB⊥AE.
3.如图所示,在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.
(1)证明:AB⊥平面VAD;
(2)求面VAD与面VDB夹角的正切值.
变式训练
又由三垂线定理知BE⊥VD.
因此,∠AEB是所求二面角的平面角.
于是,
即平面VAD与平面VDB夹角的正切值为.
探究新知
特别注意:
二面角的大小与其两个半平面的法向量的夹角有何关系?
条件
图形
关系
计算
θ=φ
θ=π-φ
cos θ=-cos φ
cos θ=cos φ
平面α,β的法向量分别为u,v,α,β所构成的二面角的大小为θ,〈u,v〉=φ
解:(1)证明:因为△AEF是等边三角形,O为EF的中点,所以AO⊥EF.
又因为平面AEF⊥平面EFCB,AO 平面AEF,
所以AO⊥平面EFCB,所以AO⊥BE.
典例讲解
例5.如图,在四棱锥A EFCB中,△AEF为等边三角形,平面AEF⊥平面EFCB,EF∥BC,BC=4,EF=2a,∠EBC=∠FCB=60°,O为EF的中点.(1)求证:;(2)求二面角的余弦值.
(2)取的中点连接由题设知四边形是等腰梯形,所以.由(1)知平面,又平面,所以
如图建立空间直角坐标系,则
典例讲解
例5.如图,在四棱锥A EFCB中,△AEF为等边三角形,平面AEF⊥平面EFCB,EF∥BC,BC=4,EF=2a,∠EBC=∠FCB=60°,O为EF的中点.(1)求证:;(2)求二面角的余弦值.
设平面AEB的一个法向量=(x,y,z),
取z=1,则x= ,y=-1,所以(,-1,1).
又平面AEF的一个法向量为p=(0,1,0),所以cos= .
由题知二面角F -AE -B为钝角,所以它的余弦值为.
则
向量法求二面角(或其某个三角函数值)的四个步骤
方法归纳
变式训练
4.已知,如图,平面求二面角的余弦值.
解:如图建立空间直角坐标系,则A(0,0,0),B(,1,0),C(0,1,0),P(0,0,1),=(0,0,1), =(,1,0), =(,0,0), =
设平面PAB的法向量为m=(x,y,z),则
解得令x=1,则m=(1, ,0).
设平面PBC的法向量为n=(x′,y′,z′),
变式训练
4.已知,如图,平面求二面角的余弦值.
解得令,则
所以cos==.
故二面角A- PB -C的余弦值为.
则
求二面角的常用方法:
素养提炼
(1)定义法
需要紧扣它的三个条件:这个角的顶点是否在棱上;角的两边是否分别在两个半平面内;这两边是否都与棱垂直.
(2)利用三垂线定理及其逆定理求二面角
用三垂线定理或其逆定理作二面角的平面角是常用的一种方法.作垂线时,确定垂足的位置非常重要,要以利于求解为目的.
求二面角的常用方法:
素养提炼
(3)射影面积法
用公式,其中是射影面积,是原图形的面积
(4)向量法求二面角
①利用向量夹角公式求解
②利用法向量求解
D
1.如图,P是二面角α- l -β的交线l上一定点,PA α,PB β,PA⊥l,PB⊥l,∠BPA=120°,若点C是半平面α上任意一点,则∠BPC的范围为( )
A.(0°,120°) B.(0°,90°)
C.(90°,120°] D.[90°,120°]
当PC与l重合时,,当PC与PA重合时,
.故∠BPC的范围为[,].
当堂练习
解析
2. 四边形是正方形,平面,且.求:
(1)二面角的平面角的度数________;
(2) 二面角的平面角的度数________;
(3)二面角的平面角的度数________.
(1)因为平面,所以.
因为四边形为正方形,所以.
又所以平面.
又平面,所以平面平面.
所以二面角的平面角的度数为.
当堂练习
解析
2. 四边形是正方形,平面,且.求:
(1)二面角的平面角的度数________;
(2) 二面角的平面角的度数________;
(3)二面角的平面角的度数________.
当堂练习
解析
(2)因为平面,所以.
所以为二面角的平面角.
又由题意知
所以二面角的平面角的度数为.
2. 四边形是正方形,平面,且.求:
(1)二面角的平面角的度数________;
(2) 二面角的平面角的度数________;
(3)二面角的平面角的度数________.
当堂练习
解析
(3)因为平面,所以,.
所以为二面角的平面角.
又四边形为正方形,所以
所以二面角的平面角的度数为.
设正四棱锥的高为h,底面边长为a,
3.已知正四棱锥(底面为正方形,各侧面为全等的等腰三角形)的体积为12,底面对角线的长为,求侧面与底面所成的二面角________.
则2a2=()2,所以a2=12.又a2h=12,所以h= =3.
设O为S在底面上的投影,作OE⊥CD于E,连接SE,
可知SE⊥CD,∠SEO为所求二面角的平面角.
,所以∠SEO=60°.
所以侧面与底面所成二面角的大小为60°.
解析
当堂练习
当堂练习
4.三棱锥中,平面ABD与平面BCD的法向量分别为,若,则二面角的大小为( )
A. B. C. 或 D.或
当二面角为锐角时,它等于.
当二面角为钝角时,它应对等于.
解析
当堂练习
5.在正方体中,E为的中点,则平面
与平面所成的锐二面角的余弦值为________.
建系如图,设正方体的棱长为1,则D(0,0,0), (1,0,1),,
设平面的一个法向量为n = ( x , y , z ),
则,且.即
解析
当堂练习
5.在正方体中,E为的中点,则平面
与平面所成的锐二面角的余弦值为________.
令,得.
又平面的一个法向量为.
则.
归纳小结
二面角
二面角及其平面角的概念
二面角的度量
二面角的求法
定义法
向量法
三垂线定理法
射影面积法
作 业
课本P52页练习第1,3题
P52页练习第2,3题
复习引入
直线与平面的夹角
直线与平面所成角
最小角定理
直线与平面所成角的求法
概念
范围
定义法
向量法
人教B版同步教材名师课件
二面角
学习目标
学 习 目 标 核心素养
理解二面角及其平面角的概念 数学抽象
会利用定义法求二面角的大小 逻辑推理和直观想象
会用向量法求二面角的大小 直观想象和数学运算
学习目标
重点:理解二面角及二面角的平面角的定义,会求二面角的大小.
难点:求二面角大小的基本方法及步骤.
我们知道,地球绕太阳公转的轨道平面称为“黄道面’’.黄道面与地球赤道面交角(二面角的平面角)约为23°26′,它与天球相交的大圆为“黄道’’.
探究新知
黄道及其附近的南北共宽18°以内的区域为黄道带.黄道带内有十二个星座,称 为“黄道十二宫’’,从春分(节气)点起,每30°便是一宫,并冠以星座名,如白羊座、金牛座、双子座等等这便是星座的由来,今天我们研究的问题便是二面角的平面角问题.
半平面
半平面
半平面
探究点1 二面角
探究新知
从一条直线出发的两个半平面所组成的图形叫做二面角.这条直线叫做二面角的棱,这两个半平面叫做二面角的面.
记为:二面角
简记:
二面角的定义
探究新知
探究点1 二面角
(1)直立式:
(2)正卧式:
(3)平卧式:
二面角的画法
探究新知
β
2.二面角的取值范围:
二面角的平面角
说明:1.平面角的两边分别在二面角的两个面内,分别垂直于二面角的棱.
探究新知
即为二面角的平面角
提醒:二面角的大小等于它的平面角大小,平面角是直角的二面角称为直二面角
β
平面角的大小与棱上点的选取无关.
探究新知
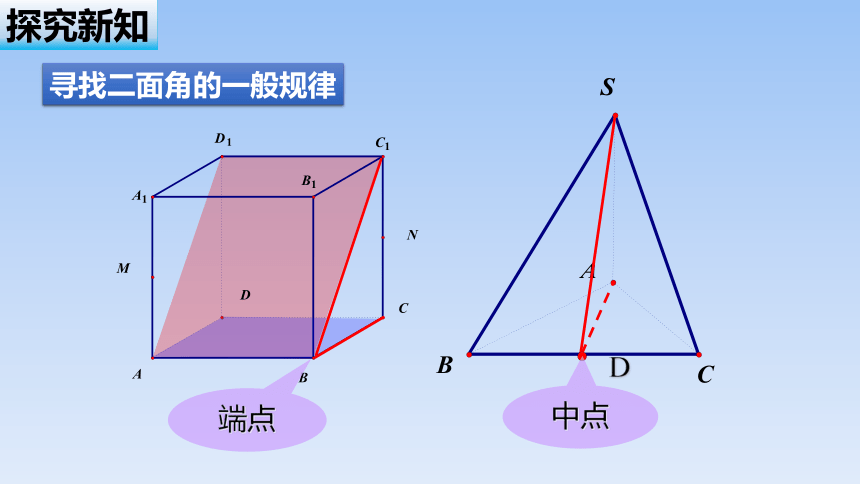
∠的大小与点在上的位置有关系吗 为什么
D
端点
中点
寻找二面角的一般规律
探究新知
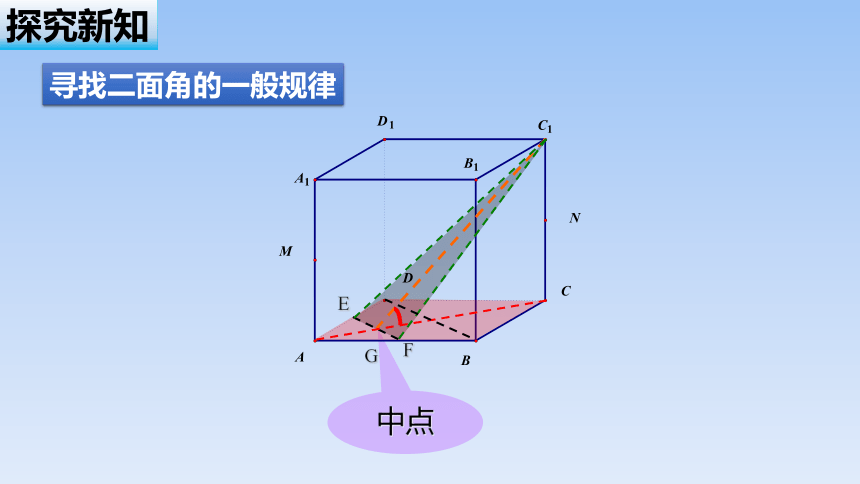
中点
E
G
F
探究新知
寻找二面角的一般规律
例1.判断正误.
(1)两个相交平面组成的图形叫做二面角 ( )
(2)异面直线分别和一个二面角的两个半平面垂直,则所成的角与这个
二面角的平面角相等或互补( )
(3)二面角的平面角是从棱上一点出发,分别在两个半平面内作射线所成角
的最小角( )
(4)二面角的大小与其平面角的顶点在棱上的位置没有关系( )
×
×
√
√
典例讲解
典例讲解
例2.如图所示,在正方体中,求二面角的大小.
解:连接和.
由已知有面
所以,
因此即为二面角的平面角
由于是等腰直角三角形,因此,
所以二面角的大小为45°
方法一:(定义法)在二面角的棱上找一个特殊点,在两个半平面内分别作垂直于棱的射线.如图所示,为二面角的平面角.
方法二:(三垂线定理法)当二面角是一个锐角时,过其中一个半平面内一点,作另一个半平面的垂线段,过(或)作棱的垂线(或),连接(或)即可.如果二面角的大小为, 则.
探究新知
思考:如何找二面角的平面角?
典例讲解
例3.如图所示,已知二面角的棱上有 ,两个点, , , , 若 ,,,求二面角的大小.
解:如图所示,在平面内过作的平行线,且使得,连接.
因为四边形是一个矩形,是二面角的一个平面角,且面,所以面,从而.
典例讲解
例3.如图所示,已知二面角的棱上有 ,两个点, , , , 若 ,,,求二面角的大小.
在中,由余弦定理可知
因此
即所求二面角的大小为.
典例讲解
例4.如图所示三棱锥面中,面面,,且,求二面角的大小.
解: 设别为的中点,连接.如图所示.
因为,所以,又因为面面,
所以面,因此在平面内的射影为.
又因为为的中位线,,所以,
从而由三垂线定理可知,
因此为二面角的一个平面角.
典例讲解
例4.如图所示三棱锥面中,面面,,且,求二面角的大小.
由且可知 ,又因为.
而且,从而可知,
即所求二面角的大小为.
定义法求二面角的一般步骤
方法归纳
简称为“一作二证三求’’
三垂线定理法求二面角的一般步骤
方法归纳
在其中一个面内找一个特殊点作另一个面的垂线
过垂足作棱的垂线(或过这个特殊点作棱的垂线)
连接特殊点与垂足(或两个垂足),根据三垂线定理或其逆定理)得二面角的平面角
变式训练
1.如图,在正方体中,求二面角的正切值
解:取的中点,连接,
由题意知,又,为的中点,
所以,
所以即是二面角的平面角,
因为平面,平面,
所以⊥.
变式训练
1.如图,在正方体中,求二面角的正切值
设正方体的棱长为,则,
在中,.
所以二面角的正切值为.
2.如果二面角α -l- β的平面角是锐角,点P到α、β和棱l的距离分别为2、4和4,求其二面角的大小.
解:①当点P在二面角α- l -β的内部时,如图①.
因为PA⊥α,所以PA⊥l.
因为AC⊥l,所以l⊥平面PAC.同理,l⊥平面PBC,
而平面PAC∩平面PBC=PC,
所以平面PAC与平面PBC应重合.
即A、C、B、P在同一平面内.
所以∠ACB是二面角α- l -β的平面角.
变式训练
2.如果二面角α -l- β的平面角是锐角,点P到α、β和棱l的距离分别为2、4和4,求其二面角的大小.
在Rt△APC中, .所以.
在Rt△BPC中,.所以.
所以.
②当点P在二面角α -l- β的外部时,如图②.
同理可得.
综上,知所求二面角的大小为或.
变式训练
3.如图所示,在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.
(1)证明:AB⊥平面VAD;
(2)求面VAD与面VDB夹角的正切值.
变式训练
解:(1)证明:
∵平面VAD⊥平面ABCD,交线为AD.
AB 平面ABCD,AB⊥AD.
∴AB⊥平面VAD.
(2)如图,取VD的中点E,连接AE,BE.
∵△VAD是正三角形,∴AE⊥VD,.
∵AB⊥平面VAD,∴AB⊥AE.
3.如图所示,在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.
(1)证明:AB⊥平面VAD;
(2)求面VAD与面VDB夹角的正切值.
变式训练
又由三垂线定理知BE⊥VD.
因此,∠AEB是所求二面角的平面角.
于是,
即平面VAD与平面VDB夹角的正切值为.
探究新知
特别注意:
二面角的大小与其两个半平面的法向量的夹角有何关系?
条件
图形
关系
计算
θ=φ
θ=π-φ
cos θ=-cos φ
cos θ=cos φ
平面α,β的法向量分别为u,v,α,β所构成的二面角的大小为θ,〈u,v〉=φ
解:(1)证明:因为△AEF是等边三角形,O为EF的中点,所以AO⊥EF.
又因为平面AEF⊥平面EFCB,AO 平面AEF,
所以AO⊥平面EFCB,所以AO⊥BE.
典例讲解
例5.如图,在四棱锥A EFCB中,△AEF为等边三角形,平面AEF⊥平面EFCB,EF∥BC,BC=4,EF=2a,∠EBC=∠FCB=60°,O为EF的中点.(1)求证:;(2)求二面角的余弦值.
(2)取的中点连接由题设知四边形是等腰梯形,所以.由(1)知平面,又平面,所以
如图建立空间直角坐标系,则
典例讲解
例5.如图,在四棱锥A EFCB中,△AEF为等边三角形,平面AEF⊥平面EFCB,EF∥BC,BC=4,EF=2a,∠EBC=∠FCB=60°,O为EF的中点.(1)求证:;(2)求二面角的余弦值.
设平面AEB的一个法向量=(x,y,z),
取z=1,则x= ,y=-1,所以(,-1,1).
又平面AEF的一个法向量为p=(0,1,0),所以cos
由题知二面角F -AE -B为钝角,所以它的余弦值为.
则
向量法求二面角(或其某个三角函数值)的四个步骤
方法归纳
变式训练
4.已知,如图,平面求二面角的余弦值.
解:如图建立空间直角坐标系,则A(0,0,0),B(,1,0),C(0,1,0),P(0,0,1),=(0,0,1), =(,1,0), =(,0,0), =
设平面PAB的法向量为m=(x,y,z),则
解得令x=1,则m=(1, ,0).
设平面PBC的法向量为n=(x′,y′,z′),
变式训练
4.已知,如图,平面求二面角的余弦值.
解得令,则
所以cos
故二面角A- PB -C的余弦值为.
则
求二面角的常用方法:
素养提炼
(1)定义法
需要紧扣它的三个条件:这个角的顶点是否在棱上;角的两边是否分别在两个半平面内;这两边是否都与棱垂直.
(2)利用三垂线定理及其逆定理求二面角
用三垂线定理或其逆定理作二面角的平面角是常用的一种方法.作垂线时,确定垂足的位置非常重要,要以利于求解为目的.
求二面角的常用方法:
素养提炼
(3)射影面积法
用公式,其中是射影面积,是原图形的面积
(4)向量法求二面角
①利用向量夹角公式求解
②利用法向量求解
D
1.如图,P是二面角α- l -β的交线l上一定点,PA α,PB β,PA⊥l,PB⊥l,∠BPA=120°,若点C是半平面α上任意一点,则∠BPC的范围为( )
A.(0°,120°) B.(0°,90°)
C.(90°,120°] D.[90°,120°]
当PC与l重合时,,当PC与PA重合时,
.故∠BPC的范围为[,].
当堂练习
解析
2. 四边形是正方形,平面,且.求:
(1)二面角的平面角的度数________;
(2) 二面角的平面角的度数________;
(3)二面角的平面角的度数________.
(1)因为平面,所以.
因为四边形为正方形,所以.
又所以平面.
又平面,所以平面平面.
所以二面角的平面角的度数为.
当堂练习
解析
2. 四边形是正方形,平面,且.求:
(1)二面角的平面角的度数________;
(2) 二面角的平面角的度数________;
(3)二面角的平面角的度数________.
当堂练习
解析
(2)因为平面,所以.
所以为二面角的平面角.
又由题意知
所以二面角的平面角的度数为.
2. 四边形是正方形,平面,且.求:
(1)二面角的平面角的度数________;
(2) 二面角的平面角的度数________;
(3)二面角的平面角的度数________.
当堂练习
解析
(3)因为平面,所以,.
所以为二面角的平面角.
又四边形为正方形,所以
所以二面角的平面角的度数为.
设正四棱锥的高为h,底面边长为a,
3.已知正四棱锥(底面为正方形,各侧面为全等的等腰三角形)的体积为12,底面对角线的长为,求侧面与底面所成的二面角________.
则2a2=()2,所以a2=12.又a2h=12,所以h= =3.
设O为S在底面上的投影,作OE⊥CD于E,连接SE,
可知SE⊥CD,∠SEO为所求二面角的平面角.
,所以∠SEO=60°.
所以侧面与底面所成二面角的大小为60°.
解析
当堂练习
当堂练习
4.三棱锥中,平面ABD与平面BCD的法向量分别为,若,则二面角的大小为( )
A. B. C. 或 D.或
当二面角为锐角时,它等于.
当二面角为钝角时,它应对等于.
解析
当堂练习
5.在正方体中,E为的中点,则平面
与平面所成的锐二面角的余弦值为________.
建系如图,设正方体的棱长为1,则D(0,0,0), (1,0,1),,
设平面的一个法向量为n = ( x , y , z ),
则,且.即
解析
当堂练习
5.在正方体中,E为的中点,则平面
与平面所成的锐二面角的余弦值为________.
令,得.
又平面的一个法向量为.
则.
归纳小结
二面角
二面角及其平面角的概念
二面角的度量
二面角的求法
定义法
向量法
三垂线定理法
射影面积法
作 业
课本P52页练习第1,3题
P52页练习第2,3题
