四年级下册数学苏教版5.1 解决问题的策略(一)课件(共19张PPT)
文档属性
| 名称 | 四年级下册数学苏教版5.1 解决问题的策略(一)课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-05 10:26:04 | ||
图片预览






文档简介
(共19张PPT)
五
解决问题的策略(一)
小宁和小春收藏的邮票枚数相同,两人共有72枚。 他们各有邮票多少枚?
72÷2=36(枚)
答:他们各有邮票36枚。
情境导入
3
怎样画图表示题目中的条件和问题呢?试着画一画。
1
和上一题相比,问题中的未知数有什么不同?
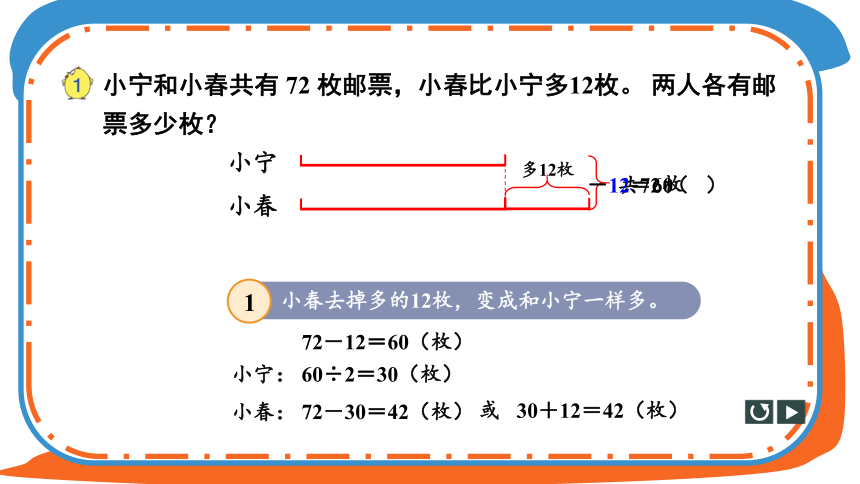
小宁和小春共有 72 枚邮票,小春比小宁多12枚。 两人各有邮票多少枚?
探究新知
2
用什么方法可以整理题目中的条件和问题呢?
探究新知
小宁
小春
多12枚
共72枚
1.文字和图画相比较,哪种更方便我们分析和思考呢?
2.从图上看,可以怎样求出两人各有邮票多少枚呢?
3.请你用喜欢的方法进行解答。
小宁和小春共有 72 枚邮票,小春比小宁多12枚。 两人各有邮票多少枚?
去多法
补少法
小宁和小春共有 72 枚邮票,小春比小宁多12枚。 两人各有邮票多少枚?
小宁
小春
共72
多12枚
-12=60
( )
枚
72-12=60(枚)
60÷2=30(枚)
小宁:
72-30=42(枚)
小春:
小春去掉多的12枚,变成和小宁一样多。
1
或 30+12=42(枚)
小宁和小春共有 72 枚邮票,小春比小宁多12枚。 两人各有邮票多少枚?
小宁
小春
共72
多12枚
+12=84
( )
枚
72+12=84(枚)
84÷2=42(枚)
小春:
72-42=30(枚)
小宁:
给小宁添上12枚,变成和小春一样多。
2
或 42-12=30(枚)
添12枚
小宁和小春共有 72 枚邮票,小春比小宁多12枚。 两人各有邮票多少枚?
比较这两种解法,它们在思路上有什么相同点和不同点呢?
都是先设法使两个人的邮票枚数变得同样多,使两个不相等的数量转化成相等的数量。
(注意:在使两个人邮票枚数变成同样多的过程中,
邮票总枚数会发生相应的变化。)
去多法
补少法
小宁和小春共有 72 枚邮票,小春比小宁多12枚。 两人各有邮票多少枚?
检验:
30+42=72(枚)
42-30=12(枚)
答:小宁有邮票30枚,小春有邮票42枚。
先检验两人邮票总数是不是72,
还要检验小春是不是比小宁多12枚。
去多法
补少法
回顾解决问题的过程,你有什么体会?
画线段图能使数量关系更直观、更清楚。
把得数代入原题检验,要符合所有已知条件。
看线段图分析数量关系,容易找到解题方法。
看图说出已知条件和问题,再解答?
巩固练习
答:科技书有60本,文艺书有45本。
【教材49页练一练】
(105+15)÷2
=120÷2
=60(本)
60-15=45(本)
方法一:
方法二:
(105-15)÷2
=90÷2
=45(本)
45+15=60(本)
检验:
45+60=105(本)
60-45=15(本)
科技书
文艺书
105本
少15本
小宁和小春共有 72 枚邮票,小春比小宁多12枚。 两人各有邮票多少枚?
科技书
文艺书
105本
少15本
看图说出已知条件和问题,再解答?
比较例1和练一练,它们在题型和解题思路上有什么相同点?
题型:
都是已知两个数量的和与差,求这两个数量。(和差问题)
思路:
借助线段图分析数量关系,想办法把两个不相等的数量转化为相等的数量。
归纳:
较大数=(和+差)÷2; 较小数=(和-差)÷2 。
答:第一小队植15棵,第二小队植19棵。
两个小队的少先队员去植树,一共植了34棵。其中第二小队比第一小队多植4棵。两个小队各植树多少棵?(先根据题意把线段图补充完整,再解答)
1.
第一小队
第二小队
4棵
34棵
(34+4)÷2
=38÷2
=19(棵)
19-4=15(棵)
方法一:
(34-4)÷2
=30÷2
=15(棵)
15+4=19(棵)
方法二:
【教材52页第1题】
答:每条短花边长20厘米,长花边长30厘米。
李娟在手工课上剪了4条花边(如下图)。
2.
(90-10)÷4
=80÷4
=20(cm)
20+10=30(cm)
方法一:
(90+10×3)÷4
=120÷4
=30(cm)
30-10=20(cm)
方法二:
想一想,哪种方法更简单一些?
【教材52页第2题】
3. 一个双层书架,上层书架的本数是下层的3倍。如果从上层搬60本到下层,那么两层书的本数正好相等。原来上、下层各有图书多少本?(在图中表示出条件和问题,再解答)
上层:60×3=180(本)
下层:60÷1=60(本)
答:上层图书有180本,下层图书有60本。
上层
下层
60本
?本
?本
(3-1)÷2=1
60+60=120(本)
180-60=120(本)
检验:180÷60=3
【教材52页第3题】
4. 小建和小西买同样的笔记本,小建买了3本,小西买了5本,小建比小西少花12元。笔记本的单价是多少元/本?(先画出线段图,再解答)
12÷(5-3)
=12÷2
=6(元/本)
答:笔记本的单价是6元/本。
小建
12元
小西
【教材52页第4题】
在以前的学习中,我们曾经运用画图的策略解决过哪些问题?
通过画一画、圈一圈,认识了一个数是另一个数的几倍。
蓝花有2朵,黄花有3个2朵,黄花的朵数是蓝花的3倍。
三年级上册
还可以这样比较黄花和蓝花的朵数:
【数学课本第4页例3】
“从条件出发分析和解决实际问题”时,初步学会了画线段图的基本方法,会用直观简练的线段图来描述数学问题了。
根据已知条件提出不同的问题,并说说怎样解答。
三年级上册
【数学课本第75页想想做做第1题】
50个
排球
足球
多15个
多20个
篮球
在以前的学习中,我们曾经运用画图的策略解决过哪些问题?
四年级上册
探索周期排列的规律时,画图表示物体的排列顺序,找出规律。
【数学课本第30页】
3盆一组,每组按“蓝花、黄花、红花”的顺序排列的。
……
蓝,黄,红,蓝,黄,红,蓝,黄,红······
在以前的学习中,我们曾经运用画图的策略解决过哪些问题?
数缺形时少直观,
形少数时难入微,
数形结合百般好,
数形隔离万事休。
——华罗庚
课堂小结
五
解决问题的策略(一)
小宁和小春收藏的邮票枚数相同,两人共有72枚。 他们各有邮票多少枚?
72÷2=36(枚)
答:他们各有邮票36枚。
情境导入
3
怎样画图表示题目中的条件和问题呢?试着画一画。
1
和上一题相比,问题中的未知数有什么不同?
小宁和小春共有 72 枚邮票,小春比小宁多12枚。 两人各有邮票多少枚?
探究新知
2
用什么方法可以整理题目中的条件和问题呢?
探究新知
小宁
小春
多12枚
共72枚
1.文字和图画相比较,哪种更方便我们分析和思考呢?
2.从图上看,可以怎样求出两人各有邮票多少枚呢?
3.请你用喜欢的方法进行解答。
小宁和小春共有 72 枚邮票,小春比小宁多12枚。 两人各有邮票多少枚?
去多法
补少法
小宁和小春共有 72 枚邮票,小春比小宁多12枚。 两人各有邮票多少枚?
小宁
小春
共72
多12枚
-12=60
( )
枚
72-12=60(枚)
60÷2=30(枚)
小宁:
72-30=42(枚)
小春:
小春去掉多的12枚,变成和小宁一样多。
1
或 30+12=42(枚)
小宁和小春共有 72 枚邮票,小春比小宁多12枚。 两人各有邮票多少枚?
小宁
小春
共72
多12枚
+12=84
( )
枚
72+12=84(枚)
84÷2=42(枚)
小春:
72-42=30(枚)
小宁:
给小宁添上12枚,变成和小春一样多。
2
或 42-12=30(枚)
添12枚
小宁和小春共有 72 枚邮票,小春比小宁多12枚。 两人各有邮票多少枚?
比较这两种解法,它们在思路上有什么相同点和不同点呢?
都是先设法使两个人的邮票枚数变得同样多,使两个不相等的数量转化成相等的数量。
(注意:在使两个人邮票枚数变成同样多的过程中,
邮票总枚数会发生相应的变化。)
去多法
补少法
小宁和小春共有 72 枚邮票,小春比小宁多12枚。 两人各有邮票多少枚?
检验:
30+42=72(枚)
42-30=12(枚)
答:小宁有邮票30枚,小春有邮票42枚。
先检验两人邮票总数是不是72,
还要检验小春是不是比小宁多12枚。
去多法
补少法
回顾解决问题的过程,你有什么体会?
画线段图能使数量关系更直观、更清楚。
把得数代入原题检验,要符合所有已知条件。
看线段图分析数量关系,容易找到解题方法。
看图说出已知条件和问题,再解答?
巩固练习
答:科技书有60本,文艺书有45本。
【教材49页练一练】
(105+15)÷2
=120÷2
=60(本)
60-15=45(本)
方法一:
方法二:
(105-15)÷2
=90÷2
=45(本)
45+15=60(本)
检验:
45+60=105(本)
60-45=15(本)
科技书
文艺书
105本
少15本
小宁和小春共有 72 枚邮票,小春比小宁多12枚。 两人各有邮票多少枚?
科技书
文艺书
105本
少15本
看图说出已知条件和问题,再解答?
比较例1和练一练,它们在题型和解题思路上有什么相同点?
题型:
都是已知两个数量的和与差,求这两个数量。(和差问题)
思路:
借助线段图分析数量关系,想办法把两个不相等的数量转化为相等的数量。
归纳:
较大数=(和+差)÷2; 较小数=(和-差)÷2 。
答:第一小队植15棵,第二小队植19棵。
两个小队的少先队员去植树,一共植了34棵。其中第二小队比第一小队多植4棵。两个小队各植树多少棵?(先根据题意把线段图补充完整,再解答)
1.
第一小队
第二小队
4棵
34棵
(34+4)÷2
=38÷2
=19(棵)
19-4=15(棵)
方法一:
(34-4)÷2
=30÷2
=15(棵)
15+4=19(棵)
方法二:
【教材52页第1题】
答:每条短花边长20厘米,长花边长30厘米。
李娟在手工课上剪了4条花边(如下图)。
2.
(90-10)÷4
=80÷4
=20(cm)
20+10=30(cm)
方法一:
(90+10×3)÷4
=120÷4
=30(cm)
30-10=20(cm)
方法二:
想一想,哪种方法更简单一些?
【教材52页第2题】
3. 一个双层书架,上层书架的本数是下层的3倍。如果从上层搬60本到下层,那么两层书的本数正好相等。原来上、下层各有图书多少本?(在图中表示出条件和问题,再解答)
上层:60×3=180(本)
下层:60÷1=60(本)
答:上层图书有180本,下层图书有60本。
上层
下层
60本
?本
?本
(3-1)÷2=1
60+60=120(本)
180-60=120(本)
检验:180÷60=3
【教材52页第3题】
4. 小建和小西买同样的笔记本,小建买了3本,小西买了5本,小建比小西少花12元。笔记本的单价是多少元/本?(先画出线段图,再解答)
12÷(5-3)
=12÷2
=6(元/本)
答:笔记本的单价是6元/本。
小建
12元
小西
【教材52页第4题】
在以前的学习中,我们曾经运用画图的策略解决过哪些问题?
通过画一画、圈一圈,认识了一个数是另一个数的几倍。
蓝花有2朵,黄花有3个2朵,黄花的朵数是蓝花的3倍。
三年级上册
还可以这样比较黄花和蓝花的朵数:
【数学课本第4页例3】
“从条件出发分析和解决实际问题”时,初步学会了画线段图的基本方法,会用直观简练的线段图来描述数学问题了。
根据已知条件提出不同的问题,并说说怎样解答。
三年级上册
【数学课本第75页想想做做第1题】
50个
排球
足球
多15个
多20个
篮球
在以前的学习中,我们曾经运用画图的策略解决过哪些问题?
四年级上册
探索周期排列的规律时,画图表示物体的排列顺序,找出规律。
【数学课本第30页】
3盆一组,每组按“蓝花、黄花、红花”的顺序排列的。
……
蓝,黄,红,蓝,黄,红,蓝,黄,红······
在以前的学习中,我们曾经运用画图的策略解决过哪些问题?
数缺形时少直观,
形少数时难入微,
数形结合百般好,
数形隔离万事休。
——华罗庚
课堂小结
