人教B版高中数学选择性必修第一册课时作业1.2.5空间中的距离(含解析)
文档属性
| 名称 | 人教B版高中数学选择性必修第一册课时作业1.2.5空间中的距离(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 657.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-05 00:00:00 | ||
图片预览



文档简介
课时分层作业(八) 空间中的距离
(建议用时:40分钟)
一、选择题
1.在平面直角坐标系中,A(-2,3),B(3,-2),沿x轴把平面直角坐标系折成120°的二面角,则AB的长为( )
A. B.2 C.3 D.4
2.已知直线l过定点A(2,3,1),且n=(0,1,1)为其一个方向向量,则点P(4,3,2)到直线l的距离为( )
A. B.
C. D.
3.如图所示,在长方体ABCD A1B1C1D1中,AD=AA1=2,AB=4,点E是棱AB的中点,则点E到平面ACD1的距离为( )
A.1 B. C. D.
4.已知正方体ABCD A1B1C1D1的棱长为a,则平面AB1D1与平面BDC1的距离为( )
A.a B.a C.a D.a
5.已知正方体ABCD A1B1C1D1的棱长为a,点E、F分别在A1B、B1D1上,且A1E=A1B,B1F=B1D1,则EF与平面ABC1D1的距离为( )
A.a B.a
C.a D.a
二、填空题
6.已知平行六面体ABCD A1B1C1D1中,以顶点A为端点的三条棱的棱长都等于2,且两两夹角都是60°,则A,C1两点间的距离是________.
7.已知棱长为1的正方体ABCD EFGH,若点P在正方体内部且满足=++,则点P到AB的距离为________.
8.如图,在三棱柱ABC A1B1C1中,所有棱长均为1,且AA1⊥底面ABC,则点B1到平面ABC1的距离为________.
三、解答题
9.在长方体ABCD-A1B1C1D1中,AB=AA1=AD=1,E,F分别是A1D1,BC的中点,P是BD上一点,PF∥平面EC1D.
(1)求BP的长;
(2)求点P到平面EC1D的距离.
10.已知正方形ABCD的边长为4,E,F分别为AD,BC的中点,以EF为棱将正方形ABCD折成如图所示的60°的二面角,点M在线段AB上且不与点A,B重合,直线MF与由A,D,E三点所确定的平面相交,交点为O.
(1)若M为AB的中点,试确定点O的位置,并证明直线OD∥平面EMC;
(2)若CE⊥MF,求AM的长度,并求此时点O到平面CDEF的距离.
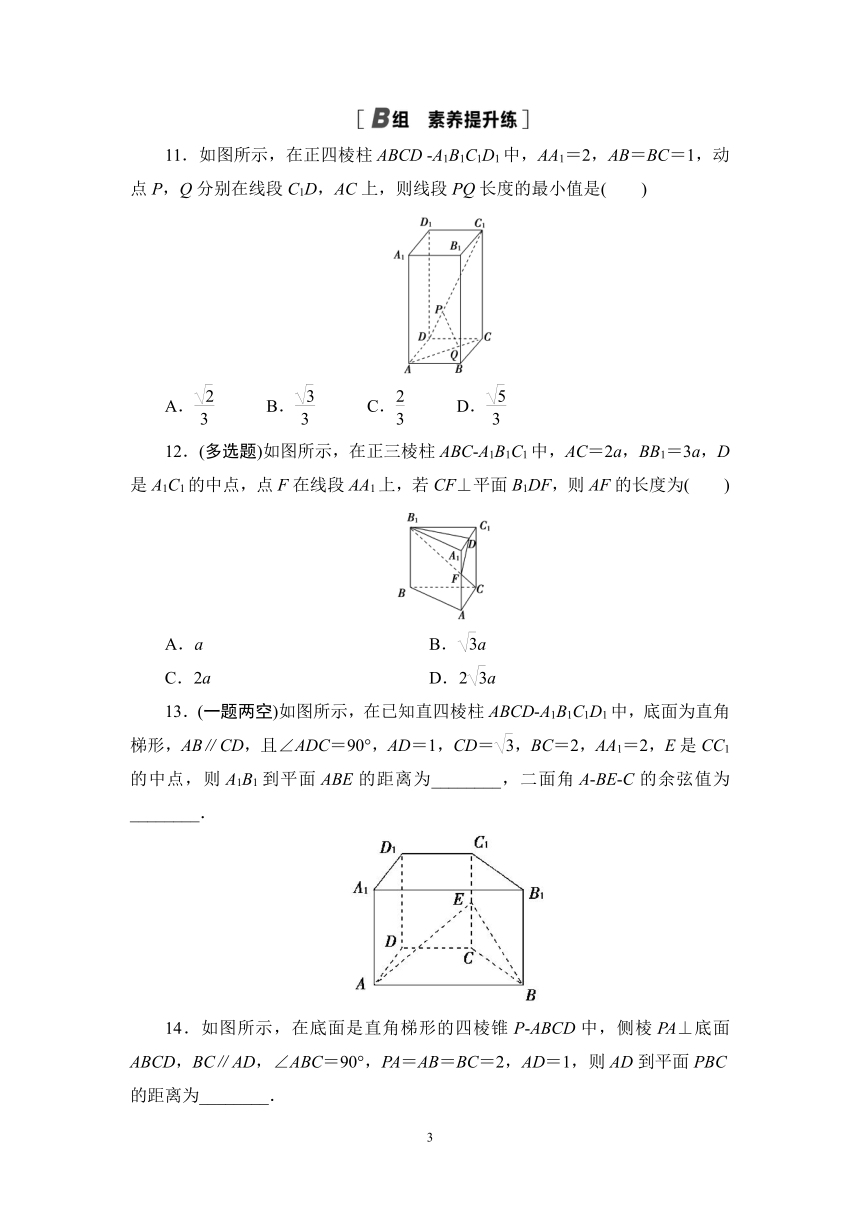
11.如图所示,在正四棱柱ABCD A1B1C1D1中,AA1=2,AB=BC=1,动点P,Q分别在线段C1D,AC上,则线段PQ长度的最小值是( )
A. B. C. D.
12.(多选题)如图所示,在正三棱柱ABC A1B1C1中,AC=2a,BB1=3a,D是A1C1的中点,点F在线段AA1上,若CF⊥平面B1DF,则AF的长度为( )
A.a B.a
C.2a D.2a
13.(一题两空)如图所示,在已知直四棱柱ABCD A1B1C1D1中,底面为直角梯形,AB∥CD,且∠ADC=90°,AD=1,CD=,BC=2,AA1=2,E是CC1的中点,则A1B1到平面ABE的距离为________,二面角A BE C的余弦值为________.
14.如图所示,在底面是直角梯形的四棱锥P ABCD中,侧棱PA⊥底面ABCD,BC∥AD,∠ABC=90°,PA=AB=BC=2,AD=1,则AD到平面PBC的距离为________.
15.如图,直四棱柱ABCD A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.
(1)证明:MN∥平面C1DE;
(2)求点C到平面C1DE的距离.
课时分层作业(八) 空间中的距离答案
(建议用时:40分钟)
一、选择题
1.在平面直角坐标系中,A(-2,3),B(3,-2),沿x轴把平面直角坐标系折成120°的二面角,则AB的长为( )
A. B.2 C.3 D.4
B [过A,B分别作x轴的垂线,垂足分别为A′,B′(图略),则||=3,||=2,||=5.又=++,所以||2=32+52+22+2×3×2×=44,即||=2.]
2.已知直线l过定点A(2,3,1),且n=(0,1,1)为其一个方向向量,则点P(4,3,2)到直线l的距离为( )
A. B.
C. D.
A [=(-2,0,-1),||=,=,则点P到直线l的距离d=eq \r(\o(|\o(PA,\s\up7(→))|2-\b\lc\|\rc\|(\a\vs4\al\co1(\f(\o(PA,\s\up7(→))·n,|n|)))))==.]
3.如图所示,在长方体ABCD A1B1C1D1中,AD=AA1=2,AB=4,点E是棱AB的中点,则点E到平面ACD1的距离为( )
A.1 B. C. D.
B [建立如图所示的坐标系A(2,0,0),D1(0,0,2),C(0,4,0),E(2,2,0),则=(-2,0,2),=(0,-4,2),=(-2,-2,2).
设平面ACD1的法向量为n=(x,y,z),
则∴
令y=1,则z=2,x=2,
∴n=(2,1,2),∴d===.]
4.已知正方体ABCD A1B1C1D1的棱长为a,则平面AB1D1与平面BDC1的距离为( )
A.a B.a C.a D.a
D [由正方体的性质,易得平面AB1D1∥平面BDC1,则两
平面间的距离可转化为点B到平面AB1D1的距离.以D为坐标原点,DA,DC,DD1所在的直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系,则A(a,0,0),B(a,a,0),A1(a,0,a),C(0,a,0),=(a,-a,a),=(0,-a,0),连接A1C,由A1C⊥平面AB1D1,得平面AB1D1的一个法向量为n=(1,-1,1),则两平面间的距离d===a.]
5.已知正方体ABCD A1B1C1D1的棱长为a,点E、F分别在A1B、B1D1上,且A1E=A1B,B1F=B1D1,则EF与平面ABC1D1的距离为( )
A.a B.a
C.a D.a
B [如图所示,建立空间直角坐标系Bxyz,易得
E,
F,
故=,
=(a,0,0),=(0,a,a).
设n=(x,y,z)是平面ABC1D1的一个法向量,
由
令z=1,得n=(0,-1,1).
∵·n=·(0,-1,1)=0,
∴⊥n,故EF∥平面ABC1D1.
又=,
∴·n=·(0,-1,1)=a,
∴d==a.]
二、填空题
6.已知平行六面体ABCD A1B1C1D1中,以顶点A为端点的三条棱的棱长都等于2,且两两夹角都是60°,则A,C1两点间的距离是________.
2 [设=a,=b,=c,易得=a+b+c,则||2=·=(a+b+c)·(a+b+c)=a2+2a·b+2a·c+2b·c+b2+c2=4+4+4+4+4+4=24,所以||=2.]
7.已知棱长为1的正方体ABCD EFGH,若点P在正方体内部且满足=++,则点P到AB的距离为________.
[建立如图所示的空间直角坐标系,则=(1,0,0)+(0,1,0)+(0,0,1)=.
=(1,0,0),·=,
所以P点到AB的距离为d===.]
8.如图,在三棱柱ABC A1B1C1中,所有棱长均为1,且AA1⊥底面ABC,则点B1到平面ABC1的距离为________.
[建立如图所示的空间直角坐标系,
则A,B(0,1,0),B1(0,1,1),C1(0,0,1),则=,=(0,1,0),=(0,1,-1).
设平面ABC1的一个法向量为n=(x,y,1),
则有
解得n=,则所求距离为==.]
三、解答题
9.在长方体ABCD-A1B1C1D1中,AB=AA1=AD=1,E,F分别是A1D1,BC的中点,P是BD上一点,PF∥平面EC1D.
(1)求BP的长;
(2)求点P到平面EC1D的距离.
[解] (1)以A1为原点,A1B1,A1D1,A1A所在直线分别为x,y,z轴,建立空间直角坐标系,
B(1,0,1),D(0,2,1),F(1,1,1),E(0,1,0),C1(1,2,0),
设P(a,b,1),=λ,λ∈[0,1],=(0,1,1),=(1,1,0),=(-1,2,0),
则=(a-1,b,0)=(-λ,2λ,0),
∴P(1-λ,2λ,1),=(λ,1-2λ,0),
设平面DEC1的法向量n=(x,y,z),
则取x=1,得n=(1,-1,1),
∵PF∥平面EC1D,
∴·n=λ-1+2λ=0,
解得λ=,
∴P,
∴BP的长||=eq \r(\b\lc\(\rc\)(\a\vs4\al\co1(\f(2,3)-1))+\b\lc\(\rc\)(\a\vs4\al\co1(\f(2,3)))+1-12)=.
(2)由(1)得平面DEC1的法向量n=(1,-1,1),=,
∴点P到平面EC1D的距离:
d===.
10.已知正方形ABCD的边长为4,E,F分别为AD,BC的中点,以EF为棱将正方形ABCD折成如图所示的60°的二面角,点M在线段AB上且不与点A,B重合,直线MF与由A,D,E三点所确定的平面相交,交点为O.
(1)若M为AB的中点,试确定点O的位置,并证明直线OD∥平面EMC;
(2)若CE⊥MF,求AM的长度,并求此时点O到平面CDEF的距离.
[解] (1)延长FM交EA的延长线于O,
∵M为AB中点,AE∥BF,∴M为OF中点,
又AB∥EF,∴A为OE中点,
连接DF交CE于N,则DO∥MN,
又DO 平面EMC,MN 平面EMC,
∴DO∥平面EMC.
(2)取AE中点H,
由题意可知,EF⊥平面DEA,EF⊥平面CFB,
∴∠DEA=∠CFB=60°,
∴△DEA与△CFB是全等的正三角形,
以H为原点建立空间坐标系如图,
设AM=t,则D(0,0,),M(1,t,0),E(-1,0,0),C(0,4,),F(-1,4,0),
∴=(-1,-4,-),=(-2,4-t,0),
∵CE⊥MF,∴·=2-16+4t=0,
解得t=
∴AM的长度为.
过O作OT⊥DE于T,则由EF⊥平面DEA,得OT⊥平面CDEF,即OT为点O到平面CDEF的距离.
∵=,∴=,
∴OA=14,OE=16,
∴OT=OEsin=16×=8.
∴点O到平面CDEF的距离为8.
11.如图所示,在正四棱柱ABCD A1B1C1D1中,AA1=2,AB=BC=1,动点P,Q分别在线段C1D,AC上,则线段PQ长度的最小值是( )
A. B. C. D.
C [建立如图所示的空间直角坐标系,则A(1,0,0),B(1,1,0),C(0,1,0),C1(0,1,2).
根据题意,可设点P的坐标为(0,λ,2λ),λ∈[0,1],点Q的坐标为(1-μ,μ,0),μ∈[0,1],
则PQ=
=
=eq \r(5\b\lc\(\rc\)(\a\vs4\al\co1(λ-\f(1,5)μ))+\f(9,5)\b\lc\(\rc\)(\a\vs4\al\co1(μ-\f(5,9)))+\f(4,9)),当且仅当λ=,μ=时,线段PQ的长度取得最小值.]
12.(多选题)如图所示,在正三棱柱ABC A1B1C1中,AC=2a,BB1=3a,D是A1C1的中点,点F在线段AA1上,若CF⊥平面B1DF,则AF的长度为( )
A.a B.a
C.2a D.2a
AC [∵CF⊥平面B1DF,∴CF⊥DF.
在矩形ACC1A1中,设AF=m.
CD2=DF2+CF2=CC+DC=10a2,①
CF2=4a2+m2,DF2=(3a-m)2+a2,②
联立①②得m=a或m=2a,则AF的长度为a或2a.]
13.(一题两空)如图所示,在已知直四棱柱ABCD A1B1C1D1中,底面为直角梯形,AB∥CD,且∠ADC=90°,AD=1,CD=,BC=2,AA1=2,E是CC1的中点,则A1B1到平面ABE的距离为________,二面角A BE C的余弦值为________.
[如图,以D为原点,、、分别为x轴、y轴、z轴建立空间直角坐标系,则A1(1,0,2),A(1,0,0),E(0,,1),
过C作AB的垂线交AB于F,易得BF=,∴B(1,2,0),
∴=(0,2,0),=(-1,-,1).
设平面ABE的一个法向量为n=(x,y,z),
则由
得
∴y=0,x=z,不妨取n=(1,0,1).
∵=(0,0,2),
∴AB1到平面ABE的距离d===.
又B1(1,2,2),∴=(0,0,2),=(1,,0).
设平面BCE的一个法向量为n=(x′,y′,z′)易得x′=-y′,z′=0,取n′=(,-1,0),n′与n所成的角为θ,
则cos θ===.]
14.如图所示,在底面是直角梯形的四棱锥P ABCD中,侧棱PA⊥底面ABCD,BC∥AD,∠ABC=90°,PA=AB=BC=2,AD=1,则AD到平面PBC的距离为________.
[由已知,得AB,AD,AP两两垂直.∴以A为坐标原点,AB,AD,AP所在的直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系,
则A(0,0,0),B(2,0,0),C(2,2,0),P(0,0,2),=(2,0,-2),=(0,2,0),设平面PBC的法向量为n=(a,b,c),则
即
∴取n=(1,0,1).
又=(2,0,0),AD∥平面PBC,
∴所求距离为=.]
15.如图,直四棱柱ABCD A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.
(1)证明:MN∥平面C1DE;
(2)求点C到平面C1DE的距离.
[解] 法一:证明:(1)连接B1C,ME,∵M,E分别是BB1,BC的中点,
∴ME∥B1C,且ME=B1C.
又N为A1D的中点,
∴ND=A1D,
由题设知A1B1DC,
∴B1CA1D,∴MEND,
∴四边形MNDE是平行四边形,所以MN∥ED,
又MN 平面C1DE,
∴MN∥平面C1DE.
(2)过C作C1E的垂线,垂足为H,
由已知可得DE⊥BC,DE⊥C1C,
∴DE⊥平面C1CE,故DE⊥CH,
∴CH⊥平面C1DE,故CH的长即为C到平面C1DE的距离,
由已知可得CE=1,CC1=4,
∴C1E=,故CH=,
∴点C到平面C1DE的距离为.
法二:证明:(1)∵直四棱柱ABCD A1B1C1D1的底面是菱形,
AA1=4,AB=2,∠BAD=60°,
E,M,N分别是BC,BB1,A1D的中点.
∴DD1⊥平面ABCD,DE⊥AD,
以D为原点,DA为x轴,DE为y轴,
DD1为z轴,建立空间直角坐标系,
M(1,,2),N(1,0,2),D(0,0,0),E(0,,0),C1(-1,,4),=(0,-,0),=(-1,,4),=(0,,0),
设平面C1DE的法向量n=(x,y,z),
则
取z=1,得n=(4,0,1),
∵·n=0,MN 平面C1DE,
∴MN∥平面C1DE.
(2)C(-1,,0),=(-1,,0),
平面C1DE的法向量n=(4,0,1),
∴点C到平面C1DE的距离
d===.
PAGE
4
(建议用时:40分钟)
一、选择题
1.在平面直角坐标系中,A(-2,3),B(3,-2),沿x轴把平面直角坐标系折成120°的二面角,则AB的长为( )
A. B.2 C.3 D.4
2.已知直线l过定点A(2,3,1),且n=(0,1,1)为其一个方向向量,则点P(4,3,2)到直线l的距离为( )
A. B.
C. D.
3.如图所示,在长方体ABCD A1B1C1D1中,AD=AA1=2,AB=4,点E是棱AB的中点,则点E到平面ACD1的距离为( )
A.1 B. C. D.
4.已知正方体ABCD A1B1C1D1的棱长为a,则平面AB1D1与平面BDC1的距离为( )
A.a B.a C.a D.a
5.已知正方体ABCD A1B1C1D1的棱长为a,点E、F分别在A1B、B1D1上,且A1E=A1B,B1F=B1D1,则EF与平面ABC1D1的距离为( )
A.a B.a
C.a D.a
二、填空题
6.已知平行六面体ABCD A1B1C1D1中,以顶点A为端点的三条棱的棱长都等于2,且两两夹角都是60°,则A,C1两点间的距离是________.
7.已知棱长为1的正方体ABCD EFGH,若点P在正方体内部且满足=++,则点P到AB的距离为________.
8.如图,在三棱柱ABC A1B1C1中,所有棱长均为1,且AA1⊥底面ABC,则点B1到平面ABC1的距离为________.
三、解答题
9.在长方体ABCD-A1B1C1D1中,AB=AA1=AD=1,E,F分别是A1D1,BC的中点,P是BD上一点,PF∥平面EC1D.
(1)求BP的长;
(2)求点P到平面EC1D的距离.
10.已知正方形ABCD的边长为4,E,F分别为AD,BC的中点,以EF为棱将正方形ABCD折成如图所示的60°的二面角,点M在线段AB上且不与点A,B重合,直线MF与由A,D,E三点所确定的平面相交,交点为O.
(1)若M为AB的中点,试确定点O的位置,并证明直线OD∥平面EMC;
(2)若CE⊥MF,求AM的长度,并求此时点O到平面CDEF的距离.
11.如图所示,在正四棱柱ABCD A1B1C1D1中,AA1=2,AB=BC=1,动点P,Q分别在线段C1D,AC上,则线段PQ长度的最小值是( )
A. B. C. D.
12.(多选题)如图所示,在正三棱柱ABC A1B1C1中,AC=2a,BB1=3a,D是A1C1的中点,点F在线段AA1上,若CF⊥平面B1DF,则AF的长度为( )
A.a B.a
C.2a D.2a
13.(一题两空)如图所示,在已知直四棱柱ABCD A1B1C1D1中,底面为直角梯形,AB∥CD,且∠ADC=90°,AD=1,CD=,BC=2,AA1=2,E是CC1的中点,则A1B1到平面ABE的距离为________,二面角A BE C的余弦值为________.
14.如图所示,在底面是直角梯形的四棱锥P ABCD中,侧棱PA⊥底面ABCD,BC∥AD,∠ABC=90°,PA=AB=BC=2,AD=1,则AD到平面PBC的距离为________.
15.如图,直四棱柱ABCD A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.
(1)证明:MN∥平面C1DE;
(2)求点C到平面C1DE的距离.
课时分层作业(八) 空间中的距离答案
(建议用时:40分钟)
一、选择题
1.在平面直角坐标系中,A(-2,3),B(3,-2),沿x轴把平面直角坐标系折成120°的二面角,则AB的长为( )
A. B.2 C.3 D.4
B [过A,B分别作x轴的垂线,垂足分别为A′,B′(图略),则||=3,||=2,||=5.又=++,所以||2=32+52+22+2×3×2×=44,即||=2.]
2.已知直线l过定点A(2,3,1),且n=(0,1,1)为其一个方向向量,则点P(4,3,2)到直线l的距离为( )
A. B.
C. D.
A [=(-2,0,-1),||=,=,则点P到直线l的距离d=eq \r(\o(|\o(PA,\s\up7(→))|2-\b\lc\|\rc\|(\a\vs4\al\co1(\f(\o(PA,\s\up7(→))·n,|n|)))))==.]
3.如图所示,在长方体ABCD A1B1C1D1中,AD=AA1=2,AB=4,点E是棱AB的中点,则点E到平面ACD1的距离为( )
A.1 B. C. D.
B [建立如图所示的坐标系A(2,0,0),D1(0,0,2),C(0,4,0),E(2,2,0),则=(-2,0,2),=(0,-4,2),=(-2,-2,2).
设平面ACD1的法向量为n=(x,y,z),
则∴
令y=1,则z=2,x=2,
∴n=(2,1,2),∴d===.]
4.已知正方体ABCD A1B1C1D1的棱长为a,则平面AB1D1与平面BDC1的距离为( )
A.a B.a C.a D.a
D [由正方体的性质,易得平面AB1D1∥平面BDC1,则两
平面间的距离可转化为点B到平面AB1D1的距离.以D为坐标原点,DA,DC,DD1所在的直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系,则A(a,0,0),B(a,a,0),A1(a,0,a),C(0,a,0),=(a,-a,a),=(0,-a,0),连接A1C,由A1C⊥平面AB1D1,得平面AB1D1的一个法向量为n=(1,-1,1),则两平面间的距离d===a.]
5.已知正方体ABCD A1B1C1D1的棱长为a,点E、F分别在A1B、B1D1上,且A1E=A1B,B1F=B1D1,则EF与平面ABC1D1的距离为( )
A.a B.a
C.a D.a
B [如图所示,建立空间直角坐标系Bxyz,易得
E,
F,
故=,
=(a,0,0),=(0,a,a).
设n=(x,y,z)是平面ABC1D1的一个法向量,
由
令z=1,得n=(0,-1,1).
∵·n=·(0,-1,1)=0,
∴⊥n,故EF∥平面ABC1D1.
又=,
∴·n=·(0,-1,1)=a,
∴d==a.]
二、填空题
6.已知平行六面体ABCD A1B1C1D1中,以顶点A为端点的三条棱的棱长都等于2,且两两夹角都是60°,则A,C1两点间的距离是________.
2 [设=a,=b,=c,易得=a+b+c,则||2=·=(a+b+c)·(a+b+c)=a2+2a·b+2a·c+2b·c+b2+c2=4+4+4+4+4+4=24,所以||=2.]
7.已知棱长为1的正方体ABCD EFGH,若点P在正方体内部且满足=++,则点P到AB的距离为________.
[建立如图所示的空间直角坐标系,则=(1,0,0)+(0,1,0)+(0,0,1)=.
=(1,0,0),·=,
所以P点到AB的距离为d===.]
8.如图,在三棱柱ABC A1B1C1中,所有棱长均为1,且AA1⊥底面ABC,则点B1到平面ABC1的距离为________.
[建立如图所示的空间直角坐标系,
则A,B(0,1,0),B1(0,1,1),C1(0,0,1),则=,=(0,1,0),=(0,1,-1).
设平面ABC1的一个法向量为n=(x,y,1),
则有
解得n=,则所求距离为==.]
三、解答题
9.在长方体ABCD-A1B1C1D1中,AB=AA1=AD=1,E,F分别是A1D1,BC的中点,P是BD上一点,PF∥平面EC1D.
(1)求BP的长;
(2)求点P到平面EC1D的距离.
[解] (1)以A1为原点,A1B1,A1D1,A1A所在直线分别为x,y,z轴,建立空间直角坐标系,
B(1,0,1),D(0,2,1),F(1,1,1),E(0,1,0),C1(1,2,0),
设P(a,b,1),=λ,λ∈[0,1],=(0,1,1),=(1,1,0),=(-1,2,0),
则=(a-1,b,0)=(-λ,2λ,0),
∴P(1-λ,2λ,1),=(λ,1-2λ,0),
设平面DEC1的法向量n=(x,y,z),
则取x=1,得n=(1,-1,1),
∵PF∥平面EC1D,
∴·n=λ-1+2λ=0,
解得λ=,
∴P,
∴BP的长||=eq \r(\b\lc\(\rc\)(\a\vs4\al\co1(\f(2,3)-1))+\b\lc\(\rc\)(\a\vs4\al\co1(\f(2,3)))+1-12)=.
(2)由(1)得平面DEC1的法向量n=(1,-1,1),=,
∴点P到平面EC1D的距离:
d===.
10.已知正方形ABCD的边长为4,E,F分别为AD,BC的中点,以EF为棱将正方形ABCD折成如图所示的60°的二面角,点M在线段AB上且不与点A,B重合,直线MF与由A,D,E三点所确定的平面相交,交点为O.
(1)若M为AB的中点,试确定点O的位置,并证明直线OD∥平面EMC;
(2)若CE⊥MF,求AM的长度,并求此时点O到平面CDEF的距离.
[解] (1)延长FM交EA的延长线于O,
∵M为AB中点,AE∥BF,∴M为OF中点,
又AB∥EF,∴A为OE中点,
连接DF交CE于N,则DO∥MN,
又DO 平面EMC,MN 平面EMC,
∴DO∥平面EMC.
(2)取AE中点H,
由题意可知,EF⊥平面DEA,EF⊥平面CFB,
∴∠DEA=∠CFB=60°,
∴△DEA与△CFB是全等的正三角形,
以H为原点建立空间坐标系如图,
设AM=t,则D(0,0,),M(1,t,0),E(-1,0,0),C(0,4,),F(-1,4,0),
∴=(-1,-4,-),=(-2,4-t,0),
∵CE⊥MF,∴·=2-16+4t=0,
解得t=
∴AM的长度为.
过O作OT⊥DE于T,则由EF⊥平面DEA,得OT⊥平面CDEF,即OT为点O到平面CDEF的距离.
∵=,∴=,
∴OA=14,OE=16,
∴OT=OEsin=16×=8.
∴点O到平面CDEF的距离为8.
11.如图所示,在正四棱柱ABCD A1B1C1D1中,AA1=2,AB=BC=1,动点P,Q分别在线段C1D,AC上,则线段PQ长度的最小值是( )
A. B. C. D.
C [建立如图所示的空间直角坐标系,则A(1,0,0),B(1,1,0),C(0,1,0),C1(0,1,2).
根据题意,可设点P的坐标为(0,λ,2λ),λ∈[0,1],点Q的坐标为(1-μ,μ,0),μ∈[0,1],
则PQ=
=
=eq \r(5\b\lc\(\rc\)(\a\vs4\al\co1(λ-\f(1,5)μ))+\f(9,5)\b\lc\(\rc\)(\a\vs4\al\co1(μ-\f(5,9)))+\f(4,9)),当且仅当λ=,μ=时,线段PQ的长度取得最小值.]
12.(多选题)如图所示,在正三棱柱ABC A1B1C1中,AC=2a,BB1=3a,D是A1C1的中点,点F在线段AA1上,若CF⊥平面B1DF,则AF的长度为( )
A.a B.a
C.2a D.2a
AC [∵CF⊥平面B1DF,∴CF⊥DF.
在矩形ACC1A1中,设AF=m.
CD2=DF2+CF2=CC+DC=10a2,①
CF2=4a2+m2,DF2=(3a-m)2+a2,②
联立①②得m=a或m=2a,则AF的长度为a或2a.]
13.(一题两空)如图所示,在已知直四棱柱ABCD A1B1C1D1中,底面为直角梯形,AB∥CD,且∠ADC=90°,AD=1,CD=,BC=2,AA1=2,E是CC1的中点,则A1B1到平面ABE的距离为________,二面角A BE C的余弦值为________.
[如图,以D为原点,、、分别为x轴、y轴、z轴建立空间直角坐标系,则A1(1,0,2),A(1,0,0),E(0,,1),
过C作AB的垂线交AB于F,易得BF=,∴B(1,2,0),
∴=(0,2,0),=(-1,-,1).
设平面ABE的一个法向量为n=(x,y,z),
则由
得
∴y=0,x=z,不妨取n=(1,0,1).
∵=(0,0,2),
∴AB1到平面ABE的距离d===.
又B1(1,2,2),∴=(0,0,2),=(1,,0).
设平面BCE的一个法向量为n=(x′,y′,z′)易得x′=-y′,z′=0,取n′=(,-1,0),n′与n所成的角为θ,
则cos θ===.]
14.如图所示,在底面是直角梯形的四棱锥P ABCD中,侧棱PA⊥底面ABCD,BC∥AD,∠ABC=90°,PA=AB=BC=2,AD=1,则AD到平面PBC的距离为________.
[由已知,得AB,AD,AP两两垂直.∴以A为坐标原点,AB,AD,AP所在的直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系,
则A(0,0,0),B(2,0,0),C(2,2,0),P(0,0,2),=(2,0,-2),=(0,2,0),设平面PBC的法向量为n=(a,b,c),则
即
∴取n=(1,0,1).
又=(2,0,0),AD∥平面PBC,
∴所求距离为=.]
15.如图,直四棱柱ABCD A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.
(1)证明:MN∥平面C1DE;
(2)求点C到平面C1DE的距离.
[解] 法一:证明:(1)连接B1C,ME,∵M,E分别是BB1,BC的中点,
∴ME∥B1C,且ME=B1C.
又N为A1D的中点,
∴ND=A1D,
由题设知A1B1DC,
∴B1CA1D,∴MEND,
∴四边形MNDE是平行四边形,所以MN∥ED,
又MN 平面C1DE,
∴MN∥平面C1DE.
(2)过C作C1E的垂线,垂足为H,
由已知可得DE⊥BC,DE⊥C1C,
∴DE⊥平面C1CE,故DE⊥CH,
∴CH⊥平面C1DE,故CH的长即为C到平面C1DE的距离,
由已知可得CE=1,CC1=4,
∴C1E=,故CH=,
∴点C到平面C1DE的距离为.
法二:证明:(1)∵直四棱柱ABCD A1B1C1D1的底面是菱形,
AA1=4,AB=2,∠BAD=60°,
E,M,N分别是BC,BB1,A1D的中点.
∴DD1⊥平面ABCD,DE⊥AD,
以D为原点,DA为x轴,DE为y轴,
DD1为z轴,建立空间直角坐标系,
M(1,,2),N(1,0,2),D(0,0,0),E(0,,0),C1(-1,,4),=(0,-,0),=(-1,,4),=(0,,0),
设平面C1DE的法向量n=(x,y,z),
则
取z=1,得n=(4,0,1),
∵·n=0,MN 平面C1DE,
∴MN∥平面C1DE.
(2)C(-1,,0),=(-1,,0),
平面C1DE的法向量n=(4,0,1),
∴点C到平面C1DE的距离
d===.
PAGE
4
