人教B版高中数学必修第一册2.1.2《一元二次方程的解集及根与系数的关系》 课件(共28张PPT)
文档属性
| 名称 | 人教B版高中数学必修第一册2.1.2《一元二次方程的解集及根与系数的关系》 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 835.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-05 00:00:00 | ||
图片预览








文档简介
(共28张PPT)
2.1 等式
2.1.2 一元二次方程新的解集及根与系数的关系
第二章 等式与不等式
学习目标
梳理一元二次方程根与系数的关系,会用根与系数的关系解决一元二次方程问题。
学习目标
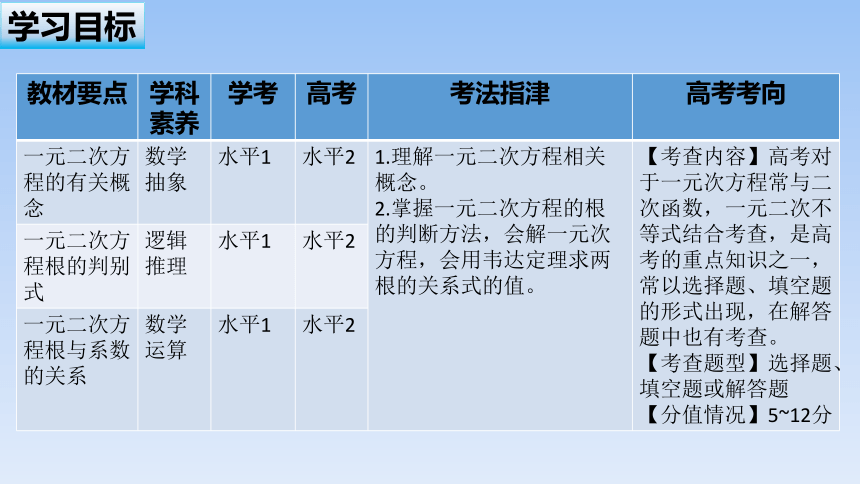
教材要点 学科素养 学考 高考 考法指津 高考考向
一元二次方程的有关概念 数学抽象 水平1 水平2 1.理解一元二次方程相关概念。 2.掌握一元二次方程的根的判断方法,会解一元次方程,会用韦达定理求两根的关系式的值。 【考查内容】高考对于一元次方程常与二次函数,一元二次不等式结合考查,是高考的重点知识之一,常以选择题、填空题的形式出现,在解答题中也有考查。
【考查题型】选择题、填空题或解答题
【分值情况】5~12分
一元二次方 程根的判别式 逻辑推理 水平1 水平2
一元二次方程根与系数的关系 数学运算 水平1 水平2
当一元二次方程ax2+bx+c=0(a≠0)的解集不是空集时,这个方程的解可以记为x1=________________,
x2=________________,且x1+x2=______,x1x2=______.
知识点一 一元二次方程根与系数的关系
(一)教材梳理填空
一、自学教材·注重基础
(二)基本知能小试
一、自学教材·注重基础
1.关于x的方程x2-4x+7=0的根是 ( )
A.x1=2+,x2=2-
B.x1=-2+,x2=-2-
C.无实数根
D.x1=2+,x2=2-
C
知识点一 一元二次方程根与系数的关系
(二)基本知能小试
一、自学教材·注重基础
知识点一 一元二次方程根与系数的关系
2.下列一元二次方程中,有两个不相等的实数根的方程是 ( )
A.x2+1=0 B.x2-2x+1=0
C.x2+2x+4=0 D.x2-x-3=0
D
3.若关于x的一元二次方程x2-2kx+k2-k+2=0没有实数根,则k的取值范围是__________.
(-∞,2)
题型一 用配方法解一元二次方程
例1、用配方法解下列方程:
(1)3x2-6x+2=0;
(2) .
解析
二、提升新知·注重综合
(1)两边同除以3,得x2-2x+=0,
移项, 得x2-2x=,
配方,得x2-2x+(-1)2=- +(-1)2,
即(x-1)2= ,∴x-1=±,
∴x1=1+,x2=1-,
∴方程的解集为.
题型一 用配方法解一元二次方程
例1、用配方法解下列方程:
(1)3x2-6x+2=0;
(2) .
解析
二、提升新知·注重综合
(2)方程两边同除以,
得,
移项,得,
配方,得,
即,
,∴方程的解集为.
方法总结
二、提升新知·注重综合
①“化”:将原方程化为一般形式,并将二次项系数化为1;
②“移”:将常数项移到方程右边;
③“配”:方程两边同时加上一次项系数一半的平方,此时,方程左边为一个完全平方式,右边为一个常数;
④“解”:若右边是非负数,则直接开平方求解;若右边是一个负数,则此方程无实数解.
题型一 用配方法解一元二次方程
用配方法解一元二次方程的步骤
变式训练
二、提升新知·注重综合
题型一 用配方法解一元二次方程
1.用配方法解一元二次方程2x2-6x+1=0时,此方程配方后可化为 ( )
A. B.
C. D.
A
变式训练
二、提升新知·注重综合
题型一 用配方法解一元二次方程
2.用配方法解下列方程:
(1)2x2+3x+1=0;
(2)5x2+3x-1=0.
解析:(1)方程两边同除以2,得,
移项得,
配方得,
即,
,方程的解集为.
变式训练
二、提升新知·注重综合
题型一 用配方法解一元二次方程
2.用配方法解下列方程:
(1)2x2+3x+1=0;
(2)5x2+3x-1=0.
解析:(2)方程两边同除以5,得,
移项得,
配方得,
即,
,方程的解集为.
二、提升新知·注重综合
题型二 利用公式法解一元二次方程
例2、用公式法解下列方法:
(1)x2-4x+10=0;
(2)(x+2)2=2x+1.
解析
(1) ,
,
,
.
方程的解集为.
(2)原方程可化为x2+2x+3=0.
∵a=1,b=2,c=3,
∴b2-4ac=22-4×1×3=-8<0,
∴此方程无实数根.
方法总结
二、提升新知·注重综合
用公式法解一元二次方程一定要先化为一般形式,并准确找出a、b、c的值,计算b2-4ac的值,判断方程根的情况,若方程有实数根,再代入求根公式求出方程的根.
题型二 利用公式法解一元二次方程
变式训练
二、提升新知·注重综合
1.一元二次方程2x2-x+1=0根的情况是 ( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法判断
题型二 利用公式法解一元二次方程
C
2.用公式法解下列方程:
(1)x2-4x+2=0; (2)2x(x-3)=-4x+5; (3)3y2+5(2y+3)=0.
解析:(1)∵b2-4ac=(-4)2-4×1×2=8,
∴,
∴x1=2+,x2=2-,
∴方程的解集为{2+,2-}.
变式训练
二、提升新知·注重综合
题型二 利用公式法解一元二次方程
2.用公式法解下列方程:
(1)x2-4x+2=0; (2)2x(x-3)=-4x+5; (3)3y2+5(2y+3)=0.
解析:(2)整理,得2x2-2x-5=0.
∵b2-4ac=(-2)2-4×2×(-5)=44,
∴,
∴x1= ,x2= ,
∴方程的解集为.
(3)整理,得3y2+10y+15=0,
∵b2-4ac=102-4×3×15=-80<0,∴原方程无实数根.
例3、(1)已知x1,x2是方程x2+6x+3=0的两个实数根,求的值;
(2)已知关于x的一元二次方程x2-(2k-1)x+k2+k-1=0有实数根.
①求k的取值范围;
②若此方程的两实数根x1,x2满足x+x=11,求k的值.
题型三 一元二次方程根与系数的关系
(1)由题知,Δ>0,x1+x2=-6,x1x2=3,
.
解析
二、提升新知·注重综合
例3、(1)已知x1,x2是方程x2+6x+3=0的两个实数根,求的值;
(2)已知关于x的一元二次方程x2-(2k-1)x+k2+k-1=0有实数根.
①求k的取值范围;
②若此方程的两实数根x1,x2满足x+x=11,求k的值.
题型三 一元二次方程根与系数的关系
(2)①∵关于x的一元二次方程x2-(2k-1)x+k2+k-1=0有实数根,
∴Δ≥0,
即[-(2k-1)]2-4×1×(k2+k-1)=-8k+5≥0,
解得k≤,即k的取值范围为.
解析
二、提升新知·注重综合
例3、(1)已知x1,x2是方程x2+6x+3=0的两个实数根,求的值;
(2)已知关于x的一元二次方程x2-(2k-1)x+k2+k-1=0有实数根.
①求k的取值范围;
②若此方程的两实数根x1,x2满足x+x=11,求k的值.
题型三 一元二次方程根与系数的关系
②由题知,x1+x2=2k-1,x1x2=k2+k-1,
=(x1+x2)2-2x1x2=(2k-1)2-2(k2+k-1)=2k2-6k+3.
∵11,∴2k2-6k+3=11,
解得k=4或k=-1,
∵k≤,∴k=-1.
解析
二、提升新知·注重综合
方法总结
二、提升新知·注重综合
在求含有一元二次方程两根的代数式的值时,利用根与系数的关系解题可起到化难为易、化繁为简的作用.在计算时,要先根据原方程求出两根之和与两根之积,再将代数式变形为局部含有两根之和与两根之积的形式,然后代入求值.
[提醒] 利用一元二次方程根与系数的关系求待定字母的值时,务必注意根与系数关系的应用前提条件,即Δ≥0.
题型三 一元二次方程根与系数的关系
变式训练
二、提升新知·注重综合
1.已知关于x的方程x2+3x+a=0有一个根为-2,则另一个根为 ( )
A.5 B.-1 C.2 D.-5
题型三 一元二次方程根与系数的关系
B
解析:设另一个根为x0,则-2+x0=-3,即x0=-1.
变式训练
2.已知关于x的一元二次方程x2+(2m+1)x+m2-2=0.
(1)若该方程有两个实数根,求m的最小整数值;
(2)若方程的两个实数根为x1,x2,且(x1-x2)2+m2=21,求m的值.
二、提升新知·注重综合
题型三 一元二次方程根与系数的关系
解析:(1)根据题意,得
Δ=(2m+1)2-4(m2-2)≥0,
解得m≥-,
∴m的最小整数值为-2.
变式训练
2.已知关于x的一元二次方程x2+(2m+1)x+m2-2=0.
(1)若该方程有两个实数根,求m的最小整数值;
(2)若方程的两个实数根为x1,x2,且(x1-x2)2+m2=21,求m的值.
二、提升新知·注重综合
题型三 一元二次方程根与系数的关系
解析:(2)根据题意,得
x1+x2=-(2m+1),x1x2=m2-2.
∵(x1-x2)2+m2=21,
∴(x1+x2)2-4x1x2+m2=(2m+1)2-4(m2-2)+m2=21.
整理得m2+4m-12=0,
解得m1=2,m2=-6.
∵m≥ -,∴m的值为2.
当堂练习
1.用配方法解方程时,下列配方错误的是 ( )
A.x2+6x-7=0化为(x+3)2=0
B.x2-5x-4=0化为
C.x2+2x-99=0化为(x+1)2=100
D.3x2-4x-2=0化为
一、基础经典题
三、训练素养·注重应用、创新
A
当堂练习
三、训练素养·注重应用、创新
2.一元二次方程(x+1)(x-3)=2x-5根的情况是 ( )
A.无实数根
B.有一个正根,一个负根
C.有两个正根,且都小于3
D.有两个正根,且有一根大于3
解析:整理,得x2-4x+2=0,配方得(x-2)2=2,解得x1=2+>3,x2=2->0.
D
当堂练习
三、训练素养·注重应用、创新
3.若α,β是一元二次方程3x2+2x-9=0的两根,则+的值是 ( )
A. B. C. D.
C
解析:由题知,,
.
4.若一元二次方程4x2+12x-1 147=0的两根为a,b,且a>b,则3a+b的值为______.
解析:配方得(2x+3)2=1 156,
解得或,即,
∴3a+b=28.
28
当堂练习
5.(1)如果-5是方程5x2+bx-10=0的一个根,求方程的另一个根及b的值;
(2)如果2+是方程x2-4x+c=0的一个根,求方程的另一个根及c的值.
解析:(1)设x为方程的另一个根,
则
当b=23时,Δ>0成立,∴
二、创新应用题
三、训练素养·注重应用、创新
当堂练习
5.(1)如果-5是方程5x2+bx-10=0的一个根,求方程的另一个根及b的值;
(2)如果2+是方程x2-4x+c=0的一个根,求方程的另一个根及c的值.
解析:(2)设y为方程的另一个根,则
当c=1时,Δ>0成立,
二、创新应用题
三、训练素养·注重应用、创新
2.1 等式
2.1.2 一元二次方程新的解集及根与系数的关系
第二章 等式与不等式
学习目标
梳理一元二次方程根与系数的关系,会用根与系数的关系解决一元二次方程问题。
学习目标
教材要点 学科素养 学考 高考 考法指津 高考考向
一元二次方程的有关概念 数学抽象 水平1 水平2 1.理解一元二次方程相关概念。 2.掌握一元二次方程的根的判断方法,会解一元次方程,会用韦达定理求两根的关系式的值。 【考查内容】高考对于一元次方程常与二次函数,一元二次不等式结合考查,是高考的重点知识之一,常以选择题、填空题的形式出现,在解答题中也有考查。
【考查题型】选择题、填空题或解答题
【分值情况】5~12分
一元二次方 程根的判别式 逻辑推理 水平1 水平2
一元二次方程根与系数的关系 数学运算 水平1 水平2
当一元二次方程ax2+bx+c=0(a≠0)的解集不是空集时,这个方程的解可以记为x1=________________,
x2=________________,且x1+x2=______,x1x2=______.
知识点一 一元二次方程根与系数的关系
(一)教材梳理填空
一、自学教材·注重基础
(二)基本知能小试
一、自学教材·注重基础
1.关于x的方程x2-4x+7=0的根是 ( )
A.x1=2+,x2=2-
B.x1=-2+,x2=-2-
C.无实数根
D.x1=2+,x2=2-
C
知识点一 一元二次方程根与系数的关系
(二)基本知能小试
一、自学教材·注重基础
知识点一 一元二次方程根与系数的关系
2.下列一元二次方程中,有两个不相等的实数根的方程是 ( )
A.x2+1=0 B.x2-2x+1=0
C.x2+2x+4=0 D.x2-x-3=0
D
3.若关于x的一元二次方程x2-2kx+k2-k+2=0没有实数根,则k的取值范围是__________.
(-∞,2)
题型一 用配方法解一元二次方程
例1、用配方法解下列方程:
(1)3x2-6x+2=0;
(2) .
解析
二、提升新知·注重综合
(1)两边同除以3,得x2-2x+=0,
移项, 得x2-2x=,
配方,得x2-2x+(-1)2=- +(-1)2,
即(x-1)2= ,∴x-1=±,
∴x1=1+,x2=1-,
∴方程的解集为.
题型一 用配方法解一元二次方程
例1、用配方法解下列方程:
(1)3x2-6x+2=0;
(2) .
解析
二、提升新知·注重综合
(2)方程两边同除以,
得,
移项,得,
配方,得,
即,
,∴方程的解集为.
方法总结
二、提升新知·注重综合
①“化”:将原方程化为一般形式,并将二次项系数化为1;
②“移”:将常数项移到方程右边;
③“配”:方程两边同时加上一次项系数一半的平方,此时,方程左边为一个完全平方式,右边为一个常数;
④“解”:若右边是非负数,则直接开平方求解;若右边是一个负数,则此方程无实数解.
题型一 用配方法解一元二次方程
用配方法解一元二次方程的步骤
变式训练
二、提升新知·注重综合
题型一 用配方法解一元二次方程
1.用配方法解一元二次方程2x2-6x+1=0时,此方程配方后可化为 ( )
A. B.
C. D.
A
变式训练
二、提升新知·注重综合
题型一 用配方法解一元二次方程
2.用配方法解下列方程:
(1)2x2+3x+1=0;
(2)5x2+3x-1=0.
解析:(1)方程两边同除以2,得,
移项得,
配方得,
即,
,方程的解集为.
变式训练
二、提升新知·注重综合
题型一 用配方法解一元二次方程
2.用配方法解下列方程:
(1)2x2+3x+1=0;
(2)5x2+3x-1=0.
解析:(2)方程两边同除以5,得,
移项得,
配方得,
即,
,方程的解集为.
二、提升新知·注重综合
题型二 利用公式法解一元二次方程
例2、用公式法解下列方法:
(1)x2-4x+10=0;
(2)(x+2)2=2x+1.
解析
(1) ,
,
,
.
方程的解集为.
(2)原方程可化为x2+2x+3=0.
∵a=1,b=2,c=3,
∴b2-4ac=22-4×1×3=-8<0,
∴此方程无实数根.
方法总结
二、提升新知·注重综合
用公式法解一元二次方程一定要先化为一般形式,并准确找出a、b、c的值,计算b2-4ac的值,判断方程根的情况,若方程有实数根,再代入求根公式求出方程的根.
题型二 利用公式法解一元二次方程
变式训练
二、提升新知·注重综合
1.一元二次方程2x2-x+1=0根的情况是 ( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法判断
题型二 利用公式法解一元二次方程
C
2.用公式法解下列方程:
(1)x2-4x+2=0; (2)2x(x-3)=-4x+5; (3)3y2+5(2y+3)=0.
解析:(1)∵b2-4ac=(-4)2-4×1×2=8,
∴,
∴x1=2+,x2=2-,
∴方程的解集为{2+,2-}.
变式训练
二、提升新知·注重综合
题型二 利用公式法解一元二次方程
2.用公式法解下列方程:
(1)x2-4x+2=0; (2)2x(x-3)=-4x+5; (3)3y2+5(2y+3)=0.
解析:(2)整理,得2x2-2x-5=0.
∵b2-4ac=(-2)2-4×2×(-5)=44,
∴,
∴x1= ,x2= ,
∴方程的解集为.
(3)整理,得3y2+10y+15=0,
∵b2-4ac=102-4×3×15=-80<0,∴原方程无实数根.
例3、(1)已知x1,x2是方程x2+6x+3=0的两个实数根,求的值;
(2)已知关于x的一元二次方程x2-(2k-1)x+k2+k-1=0有实数根.
①求k的取值范围;
②若此方程的两实数根x1,x2满足x+x=11,求k的值.
题型三 一元二次方程根与系数的关系
(1)由题知,Δ>0,x1+x2=-6,x1x2=3,
.
解析
二、提升新知·注重综合
例3、(1)已知x1,x2是方程x2+6x+3=0的两个实数根,求的值;
(2)已知关于x的一元二次方程x2-(2k-1)x+k2+k-1=0有实数根.
①求k的取值范围;
②若此方程的两实数根x1,x2满足x+x=11,求k的值.
题型三 一元二次方程根与系数的关系
(2)①∵关于x的一元二次方程x2-(2k-1)x+k2+k-1=0有实数根,
∴Δ≥0,
即[-(2k-1)]2-4×1×(k2+k-1)=-8k+5≥0,
解得k≤,即k的取值范围为.
解析
二、提升新知·注重综合
例3、(1)已知x1,x2是方程x2+6x+3=0的两个实数根,求的值;
(2)已知关于x的一元二次方程x2-(2k-1)x+k2+k-1=0有实数根.
①求k的取值范围;
②若此方程的两实数根x1,x2满足x+x=11,求k的值.
题型三 一元二次方程根与系数的关系
②由题知,x1+x2=2k-1,x1x2=k2+k-1,
=(x1+x2)2-2x1x2=(2k-1)2-2(k2+k-1)=2k2-6k+3.
∵11,∴2k2-6k+3=11,
解得k=4或k=-1,
∵k≤,∴k=-1.
解析
二、提升新知·注重综合
方法总结
二、提升新知·注重综合
在求含有一元二次方程两根的代数式的值时,利用根与系数的关系解题可起到化难为易、化繁为简的作用.在计算时,要先根据原方程求出两根之和与两根之积,再将代数式变形为局部含有两根之和与两根之积的形式,然后代入求值.
[提醒] 利用一元二次方程根与系数的关系求待定字母的值时,务必注意根与系数关系的应用前提条件,即Δ≥0.
题型三 一元二次方程根与系数的关系
变式训练
二、提升新知·注重综合
1.已知关于x的方程x2+3x+a=0有一个根为-2,则另一个根为 ( )
A.5 B.-1 C.2 D.-5
题型三 一元二次方程根与系数的关系
B
解析:设另一个根为x0,则-2+x0=-3,即x0=-1.
变式训练
2.已知关于x的一元二次方程x2+(2m+1)x+m2-2=0.
(1)若该方程有两个实数根,求m的最小整数值;
(2)若方程的两个实数根为x1,x2,且(x1-x2)2+m2=21,求m的值.
二、提升新知·注重综合
题型三 一元二次方程根与系数的关系
解析:(1)根据题意,得
Δ=(2m+1)2-4(m2-2)≥0,
解得m≥-,
∴m的最小整数值为-2.
变式训练
2.已知关于x的一元二次方程x2+(2m+1)x+m2-2=0.
(1)若该方程有两个实数根,求m的最小整数值;
(2)若方程的两个实数根为x1,x2,且(x1-x2)2+m2=21,求m的值.
二、提升新知·注重综合
题型三 一元二次方程根与系数的关系
解析:(2)根据题意,得
x1+x2=-(2m+1),x1x2=m2-2.
∵(x1-x2)2+m2=21,
∴(x1+x2)2-4x1x2+m2=(2m+1)2-4(m2-2)+m2=21.
整理得m2+4m-12=0,
解得m1=2,m2=-6.
∵m≥ -,∴m的值为2.
当堂练习
1.用配方法解方程时,下列配方错误的是 ( )
A.x2+6x-7=0化为(x+3)2=0
B.x2-5x-4=0化为
C.x2+2x-99=0化为(x+1)2=100
D.3x2-4x-2=0化为
一、基础经典题
三、训练素养·注重应用、创新
A
当堂练习
三、训练素养·注重应用、创新
2.一元二次方程(x+1)(x-3)=2x-5根的情况是 ( )
A.无实数根
B.有一个正根,一个负根
C.有两个正根,且都小于3
D.有两个正根,且有一根大于3
解析:整理,得x2-4x+2=0,配方得(x-2)2=2,解得x1=2+>3,x2=2->0.
D
当堂练习
三、训练素养·注重应用、创新
3.若α,β是一元二次方程3x2+2x-9=0的两根,则+的值是 ( )
A. B. C. D.
C
解析:由题知,,
.
4.若一元二次方程4x2+12x-1 147=0的两根为a,b,且a>b,则3a+b的值为______.
解析:配方得(2x+3)2=1 156,
解得或,即,
∴3a+b=28.
28
当堂练习
5.(1)如果-5是方程5x2+bx-10=0的一个根,求方程的另一个根及b的值;
(2)如果2+是方程x2-4x+c=0的一个根,求方程的另一个根及c的值.
解析:(1)设x为方程的另一个根,
则
当b=23时,Δ>0成立,∴
二、创新应用题
三、训练素养·注重应用、创新
当堂练习
5.(1)如果-5是方程5x2+bx-10=0的一个根,求方程的另一个根及b的值;
(2)如果2+是方程x2-4x+c=0的一个根,求方程的另一个根及c的值.
解析:(2)设y为方程的另一个根,则
当c=1时,Δ>0成立,
二、创新应用题
三、训练素养·注重应用、创新
