3.1 解决问题的策略(1)(课件)--六年级下册数学苏教版(共19张PPT)
文档属性
| 名称 | 3.1 解决问题的策略(1)(课件)--六年级下册数学苏教版(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-05 12:54:21 | ||
图片预览


文档简介
(共19张PPT)
解决问题的
策略(1)
苏教版·六年级下册
三
三年级上册
三年级下册
四年级上册
四年级下册
五年级下册
五年级上册
六年级上册
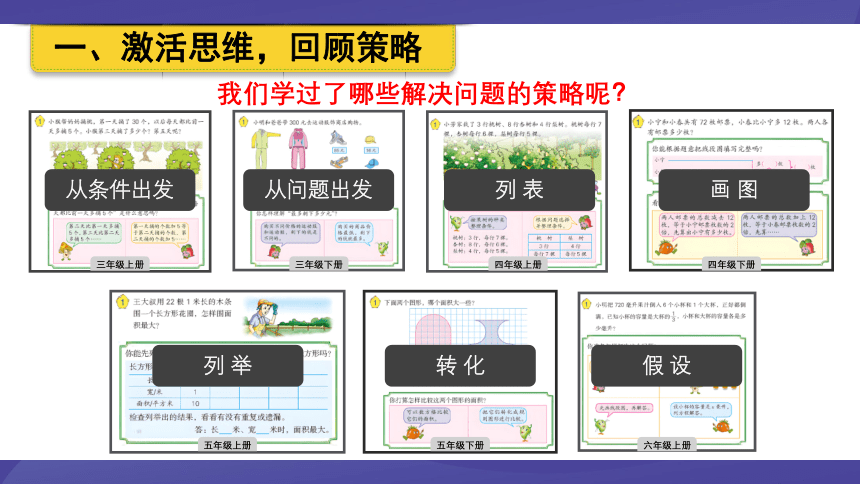
一、激活思维,回顾策略
从条件出发
从问题出发
列 表
画 图
列 举
转 化
假 设
我们学过了哪些解决问题的策略呢?
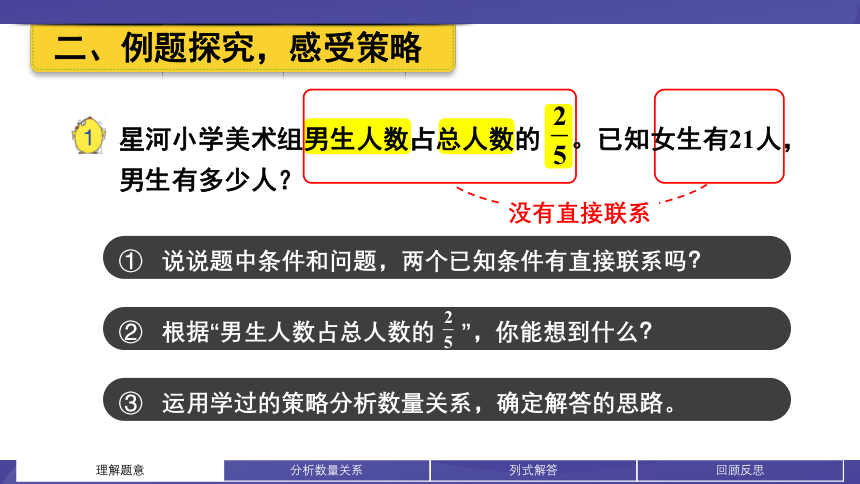
星河小学美术组男生人数占总人数的 。已知女生有21人,男生有多少人?
没有直接联系
理解题意
分析数量关系
列式解答
回顾反思
说说题中条件和问题,两个已知条件有直接联系吗?
运用学过的策略分析数量关系,确定解答的思路。
根据“男生人数占总人数的 ”,你能想到什么?
二、例题探究,感受策略
画 图
转 化
假 设
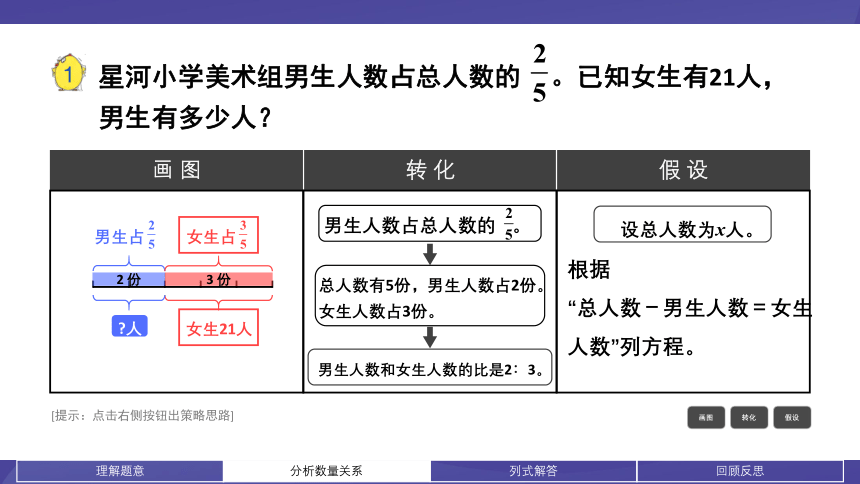
星河小学美术组男生人数占总人数的 。已知女生有21人,男生有多少人?
理解题意
分析数量关系
列式解答
回顾反思
男生占
女生21人
人
女生占
2 份
3 份
男生人数占总人数的 。
总人数有5份,男生人数占2份。
女生人数占3份。
男生人数和女生人数的比是2∶3。
设总人数为x人。
画图
转化
假设
[提示:点击右侧按钮出策略思路]
根据
“总人数-男生人数=女生人数”列方程。
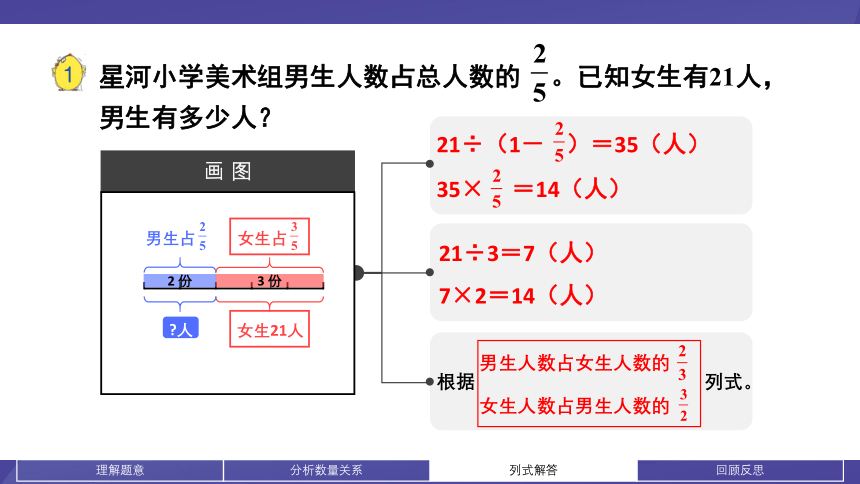
星河小学美术组男生人数占总人数的 。已知女生有21人,男生有多少人?
理解题意
分析数量关系
列式解答
回顾反思
画 图
男生占
女生21人
人
女生占
2 份
3 份
21÷(1- )=35(人)
35× =14(人)
21÷3=7(人)
7×2=14(人)
男生人数占女生人数的
女生人数占男生人数的
根据
列式。
星河小学美术组男生人数占总人数的 。已知女生有21人,男生有多少人?
理解题意
分析数量关系
列式解答
回顾反思
21÷3=7(人)
7×2=14(人)
转 化
总人数有5份,男生人数占2份。
女生人数占3份。
男生人数占总人数的 。
男生人数和女生人数的比是2∶3。
解:设总人数是x人。
x- x=21
=21
x=35
35× =14(人)
假 设
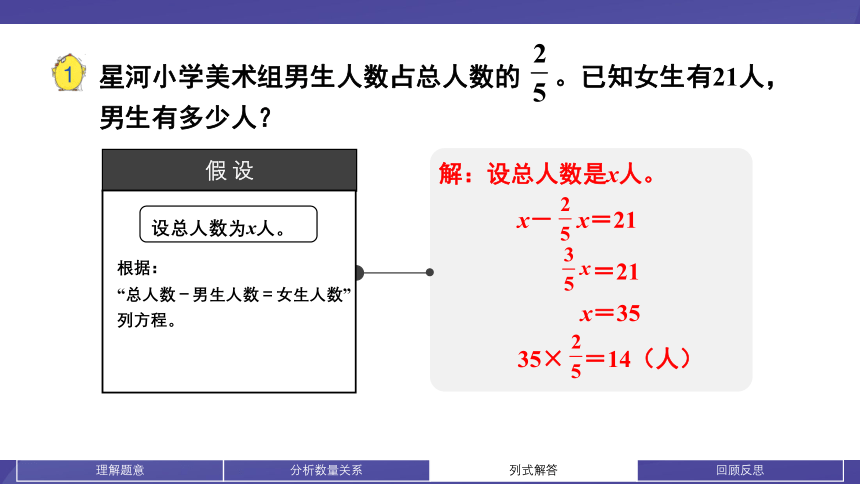
设总人数为x人。
根据:
“总人数-男生人数=女生人数”
列方程。
星河小学美术组男生人数占总人数的 。已知女生有21人,男生有多少人?
理解题意
分析数量关系
列式解答
回顾反思
星河小学美术组男生人数占总人数的 。已知女生有21人,男生有多少人?
怎样检验结果是否正确?
检验:
14+21=35(人)
14÷35=
答:男生有14人。
理解题意
分析数量关系
列式解答
回顾反思
理解题意
分析数量关系
列式解答
回顾反思
画 图
转 化
假 设
男生占
女生21人
人
女生占
2 份
3 份
男生人数占总人数的 。
总人数有5份,男生人数占2份。
男生人数和女生人数的比是2∶3。
设总人数为x人。
根据:
“总人数-男生人数=女生人数”
列方程。
21÷(1- )=35(人)
35× =14(人)
21÷3=7(人)
7×2=14(人)
解:设总人数是x人。
x- x=21
=21
x=35
35× =14(人)
比较这几种思路,说说它们之间有什么样的联系和区别?
画 图
选择画图的策略,能使数量关系更直观,更清楚。
转 化
把分数转化成比或份数,更容易理解数量之间的关系。
假 设
用假设的策略列方程,可以表示出题目中的等量关系。
回顾学习过程,说说怎样选择策略解决问题?
复杂
简单
理解题意
分析数量关系
列式解答
回顾反思
1.看图填空。
(1)一杯果汁,喝了 ,还剩 。
已喝的剩下的果汁的比是( )∶( )。
( )
( )
( )
( )
2
5
3
5
2
3
已喝的与整杯果汁的比是______;
剩下的与整杯果汁的比是______;
2∶5
3∶5
根据上面的分数和比,你还能想到哪些数量关系?
<知识点:分数与比的转化>
【教材P30练习五第1题】
三、自主练习,运用策略
(2)
花彩带与红彩带长度的比是( )∶( )。花彩带比红彩带短 ,红彩带比花彩带长 。
( )
( )
( )
( )
5
7
2
7
2
5
花彩带占总长度的______;
红彩带占总长度的______;
从不同角度对数量关系进行分析,能拓宽解决问题的思路,有助于选择合适的策略解决问题。
2. 赵大娘家养的公鸡与母鸡只数的比是4∶7,公鸡比母鸡少30只。赵大娘家养的公鸡有多少只
【教材P28练一练】
画图
公鸡:
母鸡:
?只
30只
30÷(7-4)×4=40(只)
答:公鸡有40只。
转化
公鸡与母鸡只数比是4∶7。
公鸡比母鸡少 。
30÷ =70(只)
70× =40(只)
假设
母鸡只数-公鸡只数=30只
解:设公鸡 x 只。
x-x=30
=30
x=40
2.先根据题意把线段图补充完整,再解答。
(1)一辆汽车从甲地开往乙地,已经行驶了全程的30%,离乙地还有140千米。这辆汽车行驶了多少千米
【教材P30练习五第2题】
甲地
乙地
30%
140千米
?千米
140÷7×3=60(千米)
检验:60÷(60+140)×100%=30%
答:这辆汽车行驶了60千米。
=3∶10
(2)六年级生物小组养的白兔和黑兔只数的比是5∶3,白兔比黑兔多12只。白兔和黑兔一共有多少只
白兔
黑兔
12只
?只
答:白兔和黑兔一共有48只。
12÷(5-3)
=12÷2
=6(只)
6×(5+3)
=6×8
=48(只)
3.学校举办春季运动会,参加比赛的运动员在170~180人之间,男运动员的人数是女运动员的 。
【教材P30练习五第3题】
男运动员
女运动员
170~180人
3+4=7,运动员的总人数是7的倍数,
且人数在170~180之间。
列举
总人数 170 171 172 173 174 175 176 177 178 179 180
÷7的余数
是否符合
画图
2
3
4
5
6
—
1
2
3
4
5
×
×
×
×
×
√
×
×
×
×
×
在170~180之间只有175是7的倍数,即总人数为175人。
男运动员:175× =75(人)
女运动员:175× =100(人)
答:男运动员75人,女运动员100人。
转化
男运动员
女运动员
3+4=7,运动员的总人数是7的倍数,
且人数在170~180之间。
画图
在170~180之间只有175是7的倍数,所以每份是25人。
男运动员:25×3=75(人)
女运动员:25×4=100(人)
答:男运动员75人,女运动员100人。
假设每份的人数是24人,
7×24=168;
7×25=175;
若是25人,
7×26=182;
若是26人,
假设
调整
170~180人
从接近实际结果的数据开始假设。
回顾本节课解决问题的过程,你有什么体会?
解决同一问题的策略具有多样性;一个问题,可以用不同的策略共同解决,不同的策略之间可以相互补充配合。
2
根据问题的特点灵活选择策略,分析数量关系,寻求解题思路、提高解决问题的能力。
3
画图、转化、假设、列举都是解决问题的有效策略。
1
四、回顾反思,感悟策略
解决问题的
策略(1)
苏教版·六年级下册
三
三年级上册
三年级下册
四年级上册
四年级下册
五年级下册
五年级上册
六年级上册
一、激活思维,回顾策略
从条件出发
从问题出发
列 表
画 图
列 举
转 化
假 设
我们学过了哪些解决问题的策略呢?
星河小学美术组男生人数占总人数的 。已知女生有21人,男生有多少人?
没有直接联系
理解题意
分析数量关系
列式解答
回顾反思
说说题中条件和问题,两个已知条件有直接联系吗?
运用学过的策略分析数量关系,确定解答的思路。
根据“男生人数占总人数的 ”,你能想到什么?
二、例题探究,感受策略
画 图
转 化
假 设
星河小学美术组男生人数占总人数的 。已知女生有21人,男生有多少人?
理解题意
分析数量关系
列式解答
回顾反思
男生占
女生21人
人
女生占
2 份
3 份
男生人数占总人数的 。
总人数有5份,男生人数占2份。
女生人数占3份。
男生人数和女生人数的比是2∶3。
设总人数为x人。
画图
转化
假设
[提示:点击右侧按钮出策略思路]
根据
“总人数-男生人数=女生人数”列方程。
星河小学美术组男生人数占总人数的 。已知女生有21人,男生有多少人?
理解题意
分析数量关系
列式解答
回顾反思
画 图
男生占
女生21人
人
女生占
2 份
3 份
21÷(1- )=35(人)
35× =14(人)
21÷3=7(人)
7×2=14(人)
男生人数占女生人数的
女生人数占男生人数的
根据
列式。
星河小学美术组男生人数占总人数的 。已知女生有21人,男生有多少人?
理解题意
分析数量关系
列式解答
回顾反思
21÷3=7(人)
7×2=14(人)
转 化
总人数有5份,男生人数占2份。
女生人数占3份。
男生人数占总人数的 。
男生人数和女生人数的比是2∶3。
解:设总人数是x人。
x- x=21
=21
x=35
35× =14(人)
假 设
设总人数为x人。
根据:
“总人数-男生人数=女生人数”
列方程。
星河小学美术组男生人数占总人数的 。已知女生有21人,男生有多少人?
理解题意
分析数量关系
列式解答
回顾反思
星河小学美术组男生人数占总人数的 。已知女生有21人,男生有多少人?
怎样检验结果是否正确?
检验:
14+21=35(人)
14÷35=
答:男生有14人。
理解题意
分析数量关系
列式解答
回顾反思
理解题意
分析数量关系
列式解答
回顾反思
画 图
转 化
假 设
男生占
女生21人
人
女生占
2 份
3 份
男生人数占总人数的 。
总人数有5份,男生人数占2份。
男生人数和女生人数的比是2∶3。
设总人数为x人。
根据:
“总人数-男生人数=女生人数”
列方程。
21÷(1- )=35(人)
35× =14(人)
21÷3=7(人)
7×2=14(人)
解:设总人数是x人。
x- x=21
=21
x=35
35× =14(人)
比较这几种思路,说说它们之间有什么样的联系和区别?
画 图
选择画图的策略,能使数量关系更直观,更清楚。
转 化
把分数转化成比或份数,更容易理解数量之间的关系。
假 设
用假设的策略列方程,可以表示出题目中的等量关系。
回顾学习过程,说说怎样选择策略解决问题?
复杂
简单
理解题意
分析数量关系
列式解答
回顾反思
1.看图填空。
(1)一杯果汁,喝了 ,还剩 。
已喝的剩下的果汁的比是( )∶( )。
( )
( )
( )
( )
2
5
3
5
2
3
已喝的与整杯果汁的比是______;
剩下的与整杯果汁的比是______;
2∶5
3∶5
根据上面的分数和比,你还能想到哪些数量关系?
<知识点:分数与比的转化>
【教材P30练习五第1题】
三、自主练习,运用策略
(2)
花彩带与红彩带长度的比是( )∶( )。花彩带比红彩带短 ,红彩带比花彩带长 。
( )
( )
( )
( )
5
7
2
7
2
5
花彩带占总长度的______;
红彩带占总长度的______;
从不同角度对数量关系进行分析,能拓宽解决问题的思路,有助于选择合适的策略解决问题。
2. 赵大娘家养的公鸡与母鸡只数的比是4∶7,公鸡比母鸡少30只。赵大娘家养的公鸡有多少只
【教材P28练一练】
画图
公鸡:
母鸡:
?只
30只
30÷(7-4)×4=40(只)
答:公鸡有40只。
转化
公鸡与母鸡只数比是4∶7。
公鸡比母鸡少 。
30÷ =70(只)
70× =40(只)
假设
母鸡只数-公鸡只数=30只
解:设公鸡 x 只。
x-x=30
=30
x=40
2.先根据题意把线段图补充完整,再解答。
(1)一辆汽车从甲地开往乙地,已经行驶了全程的30%,离乙地还有140千米。这辆汽车行驶了多少千米
【教材P30练习五第2题】
甲地
乙地
30%
140千米
?千米
140÷7×3=60(千米)
检验:60÷(60+140)×100%=30%
答:这辆汽车行驶了60千米。
=3∶10
(2)六年级生物小组养的白兔和黑兔只数的比是5∶3,白兔比黑兔多12只。白兔和黑兔一共有多少只
白兔
黑兔
12只
?只
答:白兔和黑兔一共有48只。
12÷(5-3)
=12÷2
=6(只)
6×(5+3)
=6×8
=48(只)
3.学校举办春季运动会,参加比赛的运动员在170~180人之间,男运动员的人数是女运动员的 。
【教材P30练习五第3题】
男运动员
女运动员
170~180人
3+4=7,运动员的总人数是7的倍数,
且人数在170~180之间。
列举
总人数 170 171 172 173 174 175 176 177 178 179 180
÷7的余数
是否符合
画图
2
3
4
5
6
—
1
2
3
4
5
×
×
×
×
×
√
×
×
×
×
×
在170~180之间只有175是7的倍数,即总人数为175人。
男运动员:175× =75(人)
女运动员:175× =100(人)
答:男运动员75人,女运动员100人。
转化
男运动员
女运动员
3+4=7,运动员的总人数是7的倍数,
且人数在170~180之间。
画图
在170~180之间只有175是7的倍数,所以每份是25人。
男运动员:25×3=75(人)
女运动员:25×4=100(人)
答:男运动员75人,女运动员100人。
假设每份的人数是24人,
7×24=168;
7×25=175;
若是25人,
7×26=182;
若是26人,
假设
调整
170~180人
从接近实际结果的数据开始假设。
回顾本节课解决问题的过程,你有什么体会?
解决同一问题的策略具有多样性;一个问题,可以用不同的策略共同解决,不同的策略之间可以相互补充配合。
2
根据问题的特点灵活选择策略,分析数量关系,寻求解题思路、提高解决问题的能力。
3
画图、转化、假设、列举都是解决问题的有效策略。
1
四、回顾反思,感悟策略
