物理人教版(2019)选择性必修第二册2.1楞次定律(共40张ppt)
文档属性
| 名称 | 物理人教版(2019)选择性必修第二册2.1楞次定律(共40张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-12-05 11:35:06 | ||
图片预览




文档简介
(共40张PPT)
第二章 电磁感应
1 楞次定律
只要使闭合电路的磁通量发生变化,闭合电路中就会有感应电流产生.
(1)电路闭合
(2)磁通量发生变化
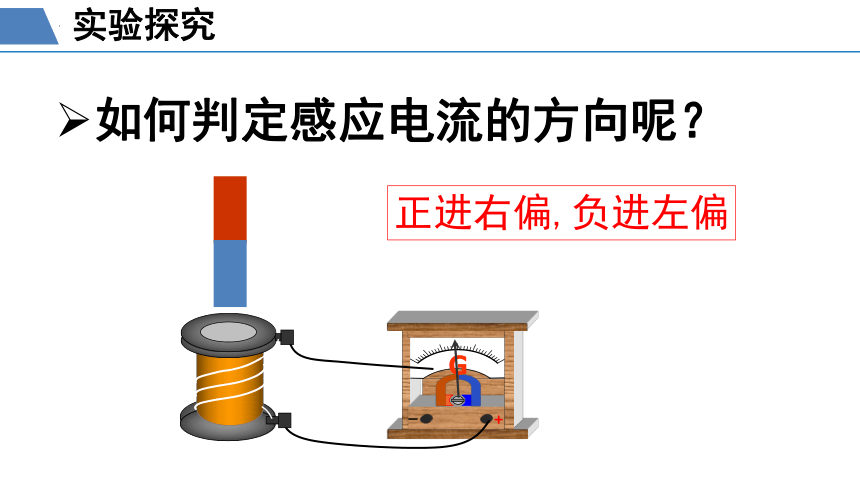
如何判定感应电流的方向呢?
+
G
正进右偏,负进左偏
实验探究
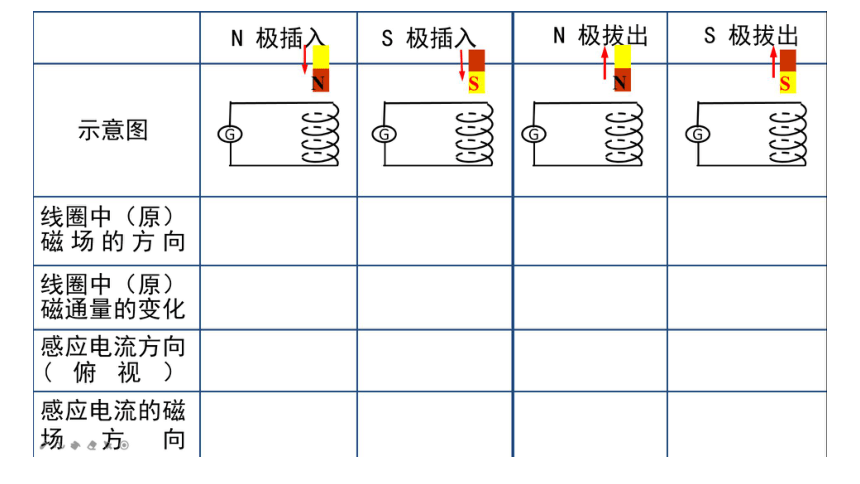
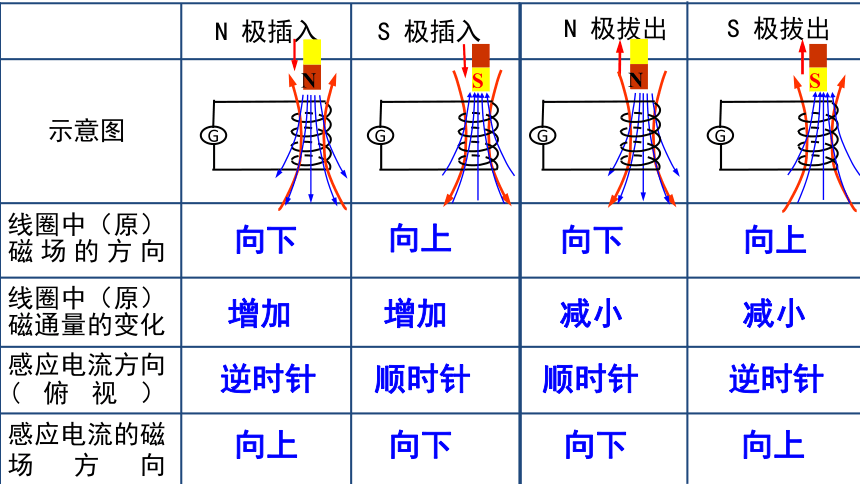
示意图
感应电流的磁场方向
感应电流方向(俯视)
线圈中(原)磁通量的变化
线圈中(原)磁场的方向
S 极拔出
S 极插入
N 极拔出
N 极插入
向下
减小
顺时针
向下
向上
向上
减小
顺时针
逆时针
向下
向上
增加
S
向下
增加
逆时针
向上
N
G
G
N
G
S
G
B感
Φ原
增
减
与
B原
与
B原
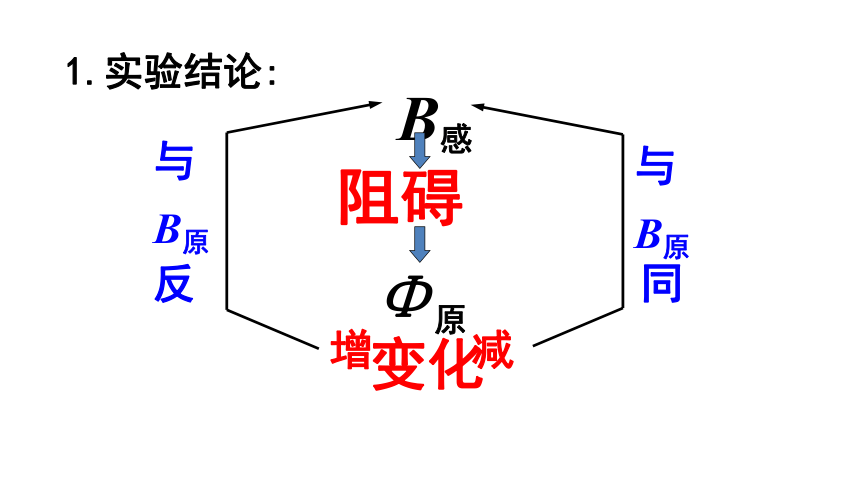
阻碍
变化
反
同
1.实验结论:
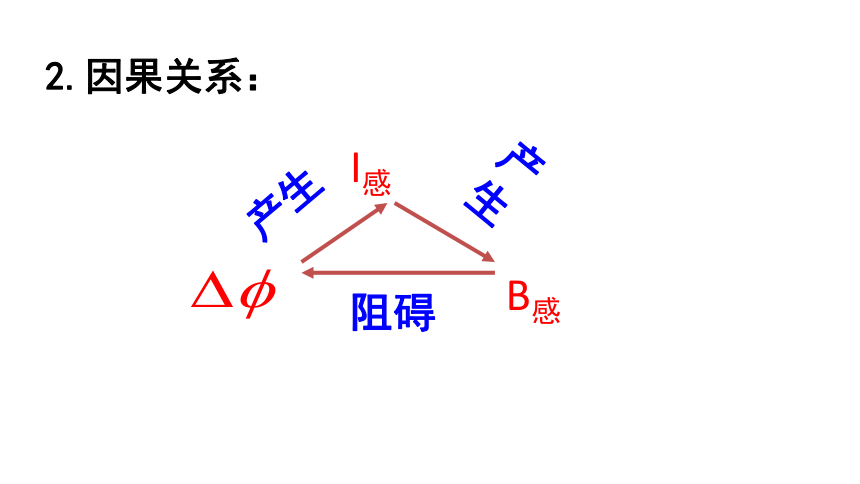
I感
B感
产生
阻碍
产生
2.因果关系:
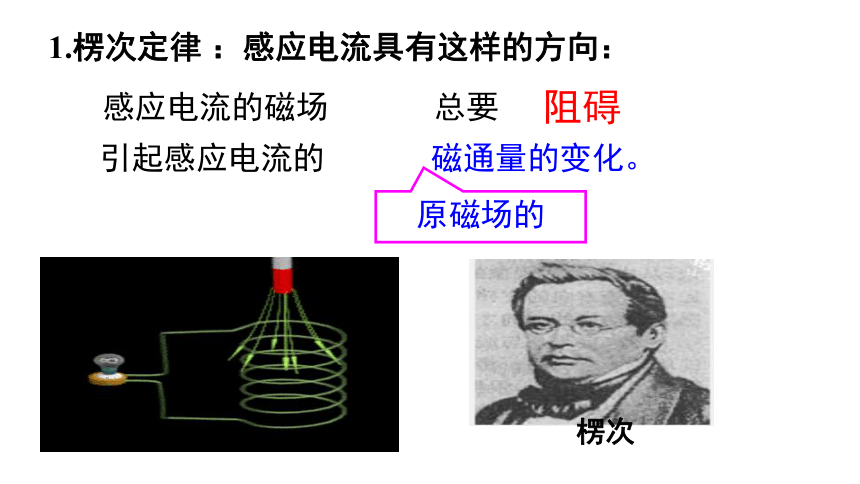
感应电流的磁场
总要
阻碍
引起感应电流的
磁通量的变化。
楞次
原磁场的
1.楞次定律 :感应电流具有这样的方向:
2.理解“阻碍”:
①谁在阻碍
②阻碍什么
③如何阻碍
感应电流的磁场
引起感应电流的原磁场磁通量的变化
“增反减同”
使磁通量的变化变慢
④结果如何
【思考】
(1)“阻碍”是否意味着“相反”.
“阻碍”并不意味着“相反”,当磁通量减少时,“阻碍”意味着“相同”.
(2)“阻碍”与“阻止”的意思相同吗?
不相同,“阻碍”不是“阻止”。阻碍是使事情不能顺利发展,该增加还是增加,该减少还是减少;阻止是使事情停止,不再向原来的方向发展了.
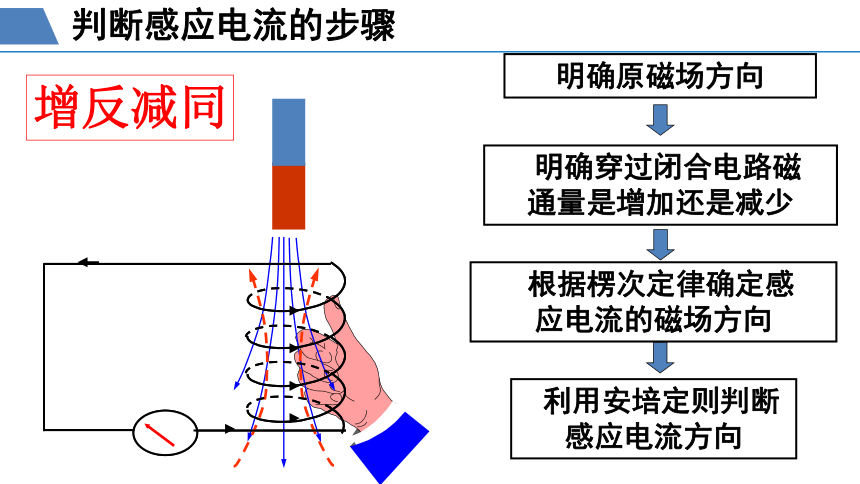
明确原磁场方向
明确穿过闭合电路磁
通量是增加还是减少
根据楞次定律确定感
应电流的磁场方向
利用安培定则判断感应电流方向
判断感应电流的步骤
增反减同
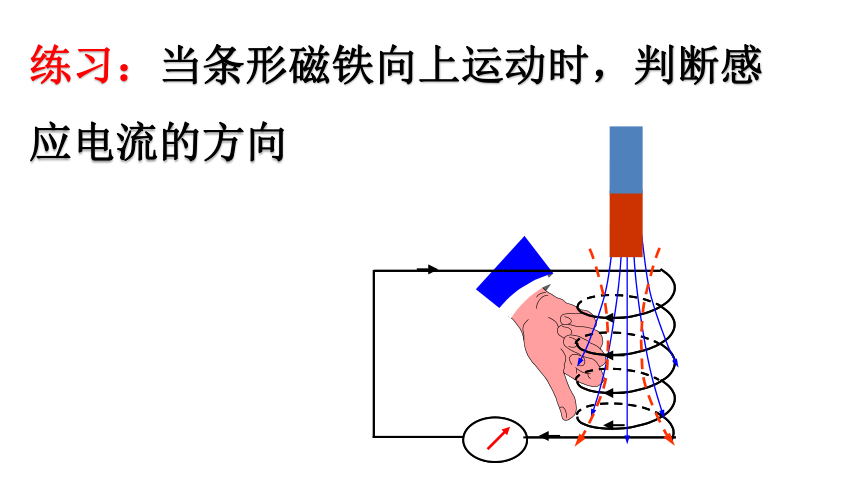
练习:当条形磁铁向上运动时,判断感应电流的方向
练习:如图,导线AB和CD互相平行,在闭合开关S时导线CD中感应电流的方向如何
I
× × × ×
× × × ×
× × × ×
练习:如图,M、N是套在同一铁芯上的两个线圈,M线圈与电池、电键、变阻器相连,N线圈与R’连成一闭合电路.当电键合上后,将图中变阻器R的滑片向左端滑动的过程中,流过电阻R’的感应电流什么方向
B感
B原
I
例:如图所示,一水平放置的矩形闭合线圈abcd在细长磁铁的N极附近竖直下落,保持bc边在纸外,ad边在纸内,由图中位置Ⅰ经过位置Ⅱ到位置Ⅲ,位置Ⅰ和位置Ⅲ都很接近位置Ⅱ,这个过程中线圈的感应电流
A.沿abcda方向
B.沿dcbad方向
C.先沿abcda方向,后沿dcbad方向
D.先沿dcbad方向,后沿abcda方向
√
逆时针
逆时针
当闭合导体的一部分做切割磁感线的运动时,怎样判断感应电流的方向 (假定导体棒AB向右运动)
1、我们研究的是哪个闭合电路
2、穿过这个闭合电路的磁通量是增大还是减小
3、感应电流的磁场应该是沿哪个方向
4、导体棒AB中的感应电流沿哪个方向
ABEF
增大
垂直纸面向外
向上
右手定则
2、适用范围:闭合电路一部分导体切割磁感线产生感应电流.
1、右手定则:伸开右手,使拇指与其余四指垂直,并且都与手掌在同一平面内;让磁感线从掌心进入,拇指指向导体运动的方向,四指所指的方向就是感应电流的方向
切割磁感线的部分导体相当于电源
①楞次定律适用于由磁通量变化引起感应电流的一切情况;右手定则只适用于导体切割磁感线。
“右手定则”是“楞次定律”的特例
②在判断导体切割磁感线产生的感应电流时右手定则比楞次定律更方便快速
3.楞次定律与右手定则:
例、在竖直向下的匀强磁场中,放在水平光滑的导轨上的两平行导线aa′,bb′,其中aa受外力作用而向左运动,试分析导线bb′向哪边运动?
I
I
F
F
a
a′
b
b′
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
发电机
电动机
v
M
楞次定律的重要结论
1.“来拒去留”法
由于磁场与导体的相对运动产生电磁感应现象时,产生的感应电流与磁场间有力的作用,这种力的作用会“阻碍”相对运动.口诀记为“来拒去留”
例 如图所示,当磁铁突然向铜环运动时,铜环的运动情况是
A.向右摆动 B.向左摆动
C.静止 D.无法判定
√
来拒去留
靠近时作用力表现为相互排斥
远离时作用力表现为彼此吸引
2.“增缩减扩”法
就闭合电路的面积而言,收缩或扩张是为了阻碍穿过电路的原磁通量的变化.若穿过闭合电路的磁通量增加,面积有收缩趋势;若穿过闭合电路的磁通量减少,面积有扩张趋势.口诀记为“增缩减扩”.说明:此法只适用于回路中只有一个方向的磁感线的情况
例 如图所示,在载流直导线旁固定有两平行光滑导轨A、B,导轨与直导线平行且在同一水平面内,在导轨上有两个可自由滑动的导体ab和cd.当载流直导线中的电流逐渐增大时,导体ab和cd的运动情况是
A.一起向左运动
B.一起向右运动
C.ab和cd相向运动,相互靠近
D.ab和cd相背运动,相互远离
√
3.“增离减靠”法
当磁场变化且线圈回路可移动时,由于磁场增强使得穿过线圈回路的磁通量增加,线圈将通过远离磁体来阻碍磁通量增加;反之,由于磁场减弱使得穿过线圈回路的磁通量减少,线圈将通过靠近磁体来阻碍磁通量减少.口诀记为“增离减靠”.
例 如图所示,通电螺线管两侧各悬挂一个小铜环,铜环平面与螺线管截面平行,当开关S接通瞬间,两铜环的运动情况为
A.同时向两侧推开
B.同时向螺线管靠拢
C.一个被推开,一个被吸引,但因电源
正负极未知,无法具体判断
D.同时被推开或同时向螺线管靠拢,但因电源正负极未知,无法具体判断
√
针对训练 如图所示,水平桌面上放有一个闭合铝环,在铝环轴线上方有一个条形磁铁.当条形磁铁沿轴线竖直向下迅速移动时,下列判断正确的是
A.铝环有扩张趋势,对桌面压力减小
B.铝环有收缩趋势,对桌面压力减小
C.铝环有收缩趋势,对桌面压力增大
D.铝环有扩张趋势,对桌面压力增大
√
总结提升
以上三种情况“殊途同归”,实质上都是以不同的方式阻碍磁通量的变化.
例 如图所示,有一垂直纸面向里的匀强磁场,磁感应强度为B,磁场有明显的圆形边界,圆心为O,半径为r.现于纸面内先后放上圆形线圈A、B、C,圆心均处于O处,线圈A的半径为r,10匝;线圈B的半径为2r,1匝;线圈C的半径为 ,1匝.
(1)在磁感应强度B减为 的过程中,线圈A和线圈B中的磁通量变化了多少?
(2)在磁场向里转过90°角与转过180°角的过程中,线圈C中的磁通量分别变化了多少?
AB磁通量始终一样
变化量依旧末减初
与匝数无关
BSsin θ
例:如图所示,a、b是两个同平面、同心放置的金属圆环,条形磁铁穿过圆环中心且与两环平面垂直,则穿过两圆环的磁通量Φa、Φb的大小关系为
A.Φa>Φb B.Φa<Φb
C.Φa=Φb D.不能比较
√
条形磁铁磁场的磁感线的分布特点是:
①磁铁内、外磁感线的条数相同
②磁铁内、外磁感线的方向相反
③磁铁外部磁感线的分布是两端密、中间疏
如果把线圈b往上移动一些,它磁通量怎么变化?
例:关于电磁感应,下列说法正确的是
A.闭合金属线圈处在变化的磁场中,一定会产生感应电流
B.闭合金属线圈在磁场中运动,一定会产生感应电流
C.闭合金属线圈中的磁通量发生变化,一定会产生感应电流
D.闭合金属线圈在磁场中转动,一定会产生感应电流
√
若线圈平面与磁场的方向平行
例 (多选)下图中能产生感应电流的是
√
√
没有闭合
闭合+S变大Φ变大
磁通量恒为0
磁通量减小
若换成一个匀强磁场?
若速度V改为向上
“三定则一定律”的综合应用
安培定则、左手定则、右手定则、楞次定律的适用场合及因果关系如下表:
比较项目 安培定则 左手定则 右手定则 楞次定律
适用场合 判断电流周围的磁感线方向 判断通电导线在磁场中所受的安培力方向 判断导体切割磁感线时产生的感应电流方向 判断回路中磁通量变化时产生的感应电流方向
因果关系 因电而生磁(I→B) 因电而受力(I、B→F安) 因动而生电(v、B→I感) 因磁通量变化而生电(ΔΦ→I感)
左力右电 切割模型第一选择用右手定则判断感应电流方向
能量的角度理解楞次定律
感应电流的产生并不是创造了能量.导体做切割磁感线运动时,产生感应电流,感应电流受到安培力作用,导体克服安培力做功从而实现其他形式能向电能的转化,所以楞次定律的“阻碍”符合能量转化和守恒
例:如图所示装置中,cd杆光滑且原来静止.当ab杆做如下哪些运动时,cd杆将向右移动(导体棒切割磁感线速度越大,感应电流越大)( )
A.向右匀速运动 B.向右加速运动
C.向左加速运动 D.向左减速运动
√
√
阻碍磁通量的变化
针对训练:(多选)如图所示,水平放置的两条光滑轨道上有可自由移动的金属棒PQ、MN,当PQ在外力的作用下运动时,MN在磁场力的作用下向右运动,则PQ所做的运动可能是(导体切割磁感线速度越大,感应电流越大)
A.向右加速运动
B.向左加速运动
C.向右减速运动
D.向左减速运动
√
√
易错:
当中间环形电流增大时,外侧线圈会收缩还是扩大
(2017·全国卷Ⅲ)如图所示,在方向垂直于纸面向里的匀强磁场中有一U形金属导轨,导轨平面与磁场垂直.金属杆PQ置于导轨上并与导轨形成闭合回路PQRS,一圆环形金属线框T位于回路围成的区域内,线框与导轨共面.现让金属杆PQ突然向右运动,在运动开始的瞬间,关于感应电流的方向,下列说法正确的是
A.PQRS中沿顺时针方向,T中沿逆时针方向
B.PQRS中沿顺时针方向,T中沿顺时针方向
C.PQRS中沿逆时针方向,T中沿逆时针方向
D.PQRS中沿逆时针方向,T中沿顺时针方向
√
阻碍磁通量的变化
第二章 电磁感应
1 楞次定律
只要使闭合电路的磁通量发生变化,闭合电路中就会有感应电流产生.
(1)电路闭合
(2)磁通量发生变化
如何判定感应电流的方向呢?
+
G
正进右偏,负进左偏
实验探究
示意图
感应电流的磁场方向
感应电流方向(俯视)
线圈中(原)磁通量的变化
线圈中(原)磁场的方向
S 极拔出
S 极插入
N 极拔出
N 极插入
向下
减小
顺时针
向下
向上
向上
减小
顺时针
逆时针
向下
向上
增加
S
向下
增加
逆时针
向上
N
G
G
N
G
S
G
B感
Φ原
增
减
与
B原
与
B原
阻碍
变化
反
同
1.实验结论:
I感
B感
产生
阻碍
产生
2.因果关系:
感应电流的磁场
总要
阻碍
引起感应电流的
磁通量的变化。
楞次
原磁场的
1.楞次定律 :感应电流具有这样的方向:
2.理解“阻碍”:
①谁在阻碍
②阻碍什么
③如何阻碍
感应电流的磁场
引起感应电流的原磁场磁通量的变化
“增反减同”
使磁通量的变化变慢
④结果如何
【思考】
(1)“阻碍”是否意味着“相反”.
“阻碍”并不意味着“相反”,当磁通量减少时,“阻碍”意味着“相同”.
(2)“阻碍”与“阻止”的意思相同吗?
不相同,“阻碍”不是“阻止”。阻碍是使事情不能顺利发展,该增加还是增加,该减少还是减少;阻止是使事情停止,不再向原来的方向发展了.
明确原磁场方向
明确穿过闭合电路磁
通量是增加还是减少
根据楞次定律确定感
应电流的磁场方向
利用安培定则判断感应电流方向
判断感应电流的步骤
增反减同
练习:当条形磁铁向上运动时,判断感应电流的方向
练习:如图,导线AB和CD互相平行,在闭合开关S时导线CD中感应电流的方向如何
I
× × × ×
× × × ×
× × × ×
练习:如图,M、N是套在同一铁芯上的两个线圈,M线圈与电池、电键、变阻器相连,N线圈与R’连成一闭合电路.当电键合上后,将图中变阻器R的滑片向左端滑动的过程中,流过电阻R’的感应电流什么方向
B感
B原
I
例:如图所示,一水平放置的矩形闭合线圈abcd在细长磁铁的N极附近竖直下落,保持bc边在纸外,ad边在纸内,由图中位置Ⅰ经过位置Ⅱ到位置Ⅲ,位置Ⅰ和位置Ⅲ都很接近位置Ⅱ,这个过程中线圈的感应电流
A.沿abcda方向
B.沿dcbad方向
C.先沿abcda方向,后沿dcbad方向
D.先沿dcbad方向,后沿abcda方向
√
逆时针
逆时针
当闭合导体的一部分做切割磁感线的运动时,怎样判断感应电流的方向 (假定导体棒AB向右运动)
1、我们研究的是哪个闭合电路
2、穿过这个闭合电路的磁通量是增大还是减小
3、感应电流的磁场应该是沿哪个方向
4、导体棒AB中的感应电流沿哪个方向
ABEF
增大
垂直纸面向外
向上
右手定则
2、适用范围:闭合电路一部分导体切割磁感线产生感应电流.
1、右手定则:伸开右手,使拇指与其余四指垂直,并且都与手掌在同一平面内;让磁感线从掌心进入,拇指指向导体运动的方向,四指所指的方向就是感应电流的方向
切割磁感线的部分导体相当于电源
①楞次定律适用于由磁通量变化引起感应电流的一切情况;右手定则只适用于导体切割磁感线。
“右手定则”是“楞次定律”的特例
②在判断导体切割磁感线产生的感应电流时右手定则比楞次定律更方便快速
3.楞次定律与右手定则:
例、在竖直向下的匀强磁场中,放在水平光滑的导轨上的两平行导线aa′,bb′,其中aa受外力作用而向左运动,试分析导线bb′向哪边运动?
I
I
F
F
a
a′
b
b′
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
发电机
电动机
v
M
楞次定律的重要结论
1.“来拒去留”法
由于磁场与导体的相对运动产生电磁感应现象时,产生的感应电流与磁场间有力的作用,这种力的作用会“阻碍”相对运动.口诀记为“来拒去留”
例 如图所示,当磁铁突然向铜环运动时,铜环的运动情况是
A.向右摆动 B.向左摆动
C.静止 D.无法判定
√
来拒去留
靠近时作用力表现为相互排斥
远离时作用力表现为彼此吸引
2.“增缩减扩”法
就闭合电路的面积而言,收缩或扩张是为了阻碍穿过电路的原磁通量的变化.若穿过闭合电路的磁通量增加,面积有收缩趋势;若穿过闭合电路的磁通量减少,面积有扩张趋势.口诀记为“增缩减扩”.说明:此法只适用于回路中只有一个方向的磁感线的情况
例 如图所示,在载流直导线旁固定有两平行光滑导轨A、B,导轨与直导线平行且在同一水平面内,在导轨上有两个可自由滑动的导体ab和cd.当载流直导线中的电流逐渐增大时,导体ab和cd的运动情况是
A.一起向左运动
B.一起向右运动
C.ab和cd相向运动,相互靠近
D.ab和cd相背运动,相互远离
√
3.“增离减靠”法
当磁场变化且线圈回路可移动时,由于磁场增强使得穿过线圈回路的磁通量增加,线圈将通过远离磁体来阻碍磁通量增加;反之,由于磁场减弱使得穿过线圈回路的磁通量减少,线圈将通过靠近磁体来阻碍磁通量减少.口诀记为“增离减靠”.
例 如图所示,通电螺线管两侧各悬挂一个小铜环,铜环平面与螺线管截面平行,当开关S接通瞬间,两铜环的运动情况为
A.同时向两侧推开
B.同时向螺线管靠拢
C.一个被推开,一个被吸引,但因电源
正负极未知,无法具体判断
D.同时被推开或同时向螺线管靠拢,但因电源正负极未知,无法具体判断
√
针对训练 如图所示,水平桌面上放有一个闭合铝环,在铝环轴线上方有一个条形磁铁.当条形磁铁沿轴线竖直向下迅速移动时,下列判断正确的是
A.铝环有扩张趋势,对桌面压力减小
B.铝环有收缩趋势,对桌面压力减小
C.铝环有收缩趋势,对桌面压力增大
D.铝环有扩张趋势,对桌面压力增大
√
总结提升
以上三种情况“殊途同归”,实质上都是以不同的方式阻碍磁通量的变化.
例 如图所示,有一垂直纸面向里的匀强磁场,磁感应强度为B,磁场有明显的圆形边界,圆心为O,半径为r.现于纸面内先后放上圆形线圈A、B、C,圆心均处于O处,线圈A的半径为r,10匝;线圈B的半径为2r,1匝;线圈C的半径为 ,1匝.
(1)在磁感应强度B减为 的过程中,线圈A和线圈B中的磁通量变化了多少?
(2)在磁场向里转过90°角与转过180°角的过程中,线圈C中的磁通量分别变化了多少?
AB磁通量始终一样
变化量依旧末减初
与匝数无关
BSsin θ
例:如图所示,a、b是两个同平面、同心放置的金属圆环,条形磁铁穿过圆环中心且与两环平面垂直,则穿过两圆环的磁通量Φa、Φb的大小关系为
A.Φa>Φb B.Φa<Φb
C.Φa=Φb D.不能比较
√
条形磁铁磁场的磁感线的分布特点是:
①磁铁内、外磁感线的条数相同
②磁铁内、外磁感线的方向相反
③磁铁外部磁感线的分布是两端密、中间疏
如果把线圈b往上移动一些,它磁通量怎么变化?
例:关于电磁感应,下列说法正确的是
A.闭合金属线圈处在变化的磁场中,一定会产生感应电流
B.闭合金属线圈在磁场中运动,一定会产生感应电流
C.闭合金属线圈中的磁通量发生变化,一定会产生感应电流
D.闭合金属线圈在磁场中转动,一定会产生感应电流
√
若线圈平面与磁场的方向平行
例 (多选)下图中能产生感应电流的是
√
√
没有闭合
闭合+S变大Φ变大
磁通量恒为0
磁通量减小
若换成一个匀强磁场?
若速度V改为向上
“三定则一定律”的综合应用
安培定则、左手定则、右手定则、楞次定律的适用场合及因果关系如下表:
比较项目 安培定则 左手定则 右手定则 楞次定律
适用场合 判断电流周围的磁感线方向 判断通电导线在磁场中所受的安培力方向 判断导体切割磁感线时产生的感应电流方向 判断回路中磁通量变化时产生的感应电流方向
因果关系 因电而生磁(I→B) 因电而受力(I、B→F安) 因动而生电(v、B→I感) 因磁通量变化而生电(ΔΦ→I感)
左力右电 切割模型第一选择用右手定则判断感应电流方向
能量的角度理解楞次定律
感应电流的产生并不是创造了能量.导体做切割磁感线运动时,产生感应电流,感应电流受到安培力作用,导体克服安培力做功从而实现其他形式能向电能的转化,所以楞次定律的“阻碍”符合能量转化和守恒
例:如图所示装置中,cd杆光滑且原来静止.当ab杆做如下哪些运动时,cd杆将向右移动(导体棒切割磁感线速度越大,感应电流越大)( )
A.向右匀速运动 B.向右加速运动
C.向左加速运动 D.向左减速运动
√
√
阻碍磁通量的变化
针对训练:(多选)如图所示,水平放置的两条光滑轨道上有可自由移动的金属棒PQ、MN,当PQ在外力的作用下运动时,MN在磁场力的作用下向右运动,则PQ所做的运动可能是(导体切割磁感线速度越大,感应电流越大)
A.向右加速运动
B.向左加速运动
C.向右减速运动
D.向左减速运动
√
√
易错:
当中间环形电流增大时,外侧线圈会收缩还是扩大
(2017·全国卷Ⅲ)如图所示,在方向垂直于纸面向里的匀强磁场中有一U形金属导轨,导轨平面与磁场垂直.金属杆PQ置于导轨上并与导轨形成闭合回路PQRS,一圆环形金属线框T位于回路围成的区域内,线框与导轨共面.现让金属杆PQ突然向右运动,在运动开始的瞬间,关于感应电流的方向,下列说法正确的是
A.PQRS中沿顺时针方向,T中沿逆时针方向
B.PQRS中沿顺时针方向,T中沿顺时针方向
C.PQRS中沿逆时针方向,T中沿逆时针方向
D.PQRS中沿逆时针方向,T中沿顺时针方向
√
阻碍磁通量的变化
