沪科版九下27.2等可能情形下的概率(二) 课件
文档属性
| 名称 | 沪科版九下27.2等可能情形下的概率(二) 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 408.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-31 12:39:56 | ||
图片预览






文档简介
课件22张PPT。27.2等可能性事件的概率
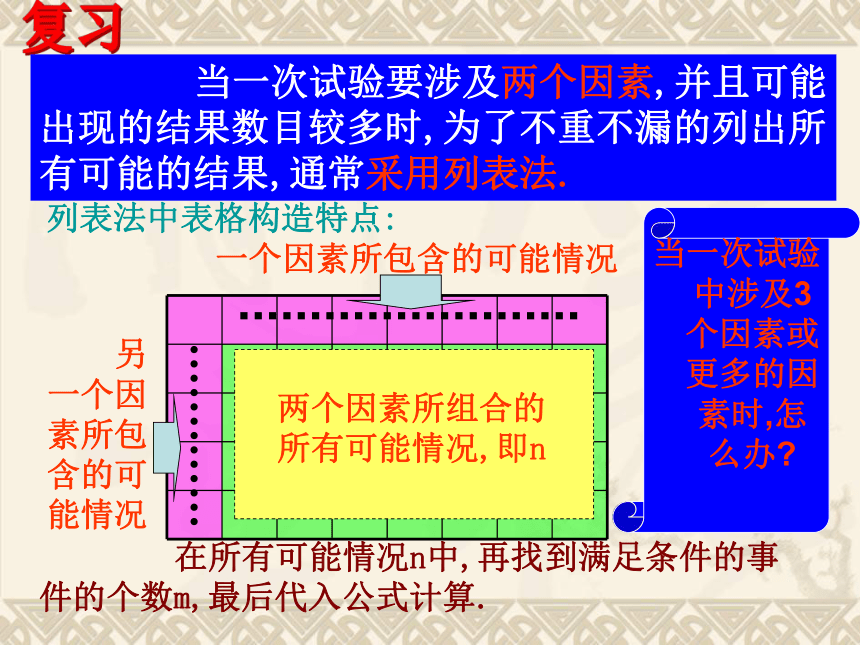
(二)复习 当一次试验要涉及两个因素,并且可能出现的结果数目较多时,为了不重不漏的列出所有可能的结果,通常采用列表法.两个因素所组合的所有可能情况,即n 在所有可能情况n中,再找到满足条件的事件的个数m,最后代入公式计算.一个因素所包含的可能情况 另一个因素所包含的可能情况列表法中表格构造特点:当一次试验中涉及3个因素或更多的因素时,怎么办?
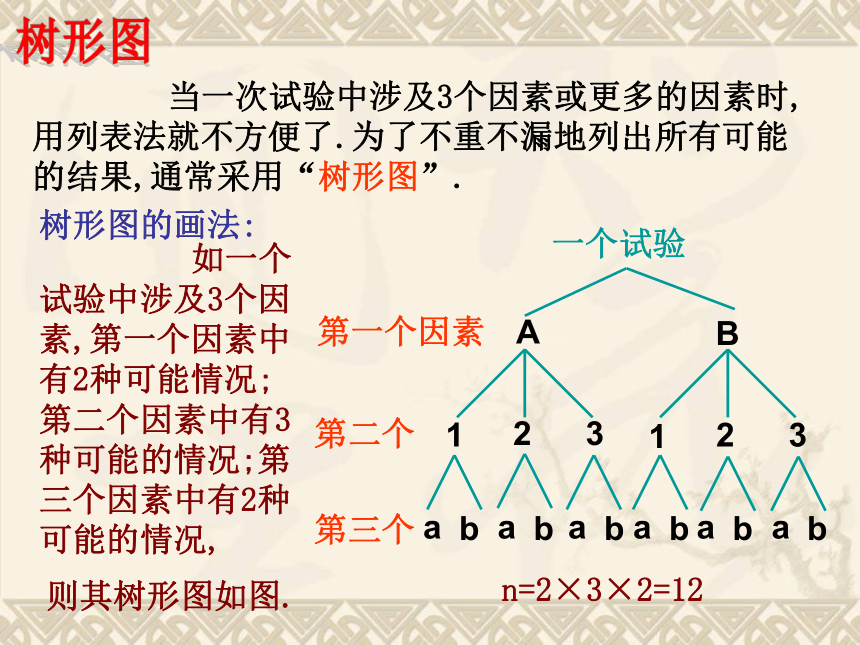
当一次试验中涉及3个因素或更多的因素时,用列表法就不方便了.为了不重不漏地列出所有可能的结果,通常采用“树形图”.树形图树形图的画法:一个试验第一个因素第二个第三个 如一个试验中涉及3个因素,第一个因素中有2种可能情况;第二个因素中有3种可能的情况;第三个因素中有2种可能的情况,AB123123abababababab则其树形图如图.n=2×3×2=12数学病院用下图所示的转盘进行“配紫色”游戏,游戏者获胜的概率是多少?刘华的思考过程如下:随机转动两个转盘,所有可能出现的结果如下:
你认为她的想法对吗,为什么?总共有9种结果,每种结果出现的可能性相同,而能够 配成紫色的结果只有一种: (红,蓝),故游戏者获胜的概率为1∕9 。用树状图或列表法求概率时,各种结果出现的可能性务必相同。 用树状图和列表的方法求概率的前提是: 各种结果出现的可能性务必相同.注意:想一想(1) 列表法和树形图法的优点是什么?
(2)什么时候使用“列表法”方便?什么时候使用“树形图法”方便?利用树形图或表格可以清晰地表示出某个事件发生的所有可能出现的结果;从而较方便地求出某些事件发生的概率.
当试验包含两步时,列表法比较方便,当然,此时也可以用树形图法;
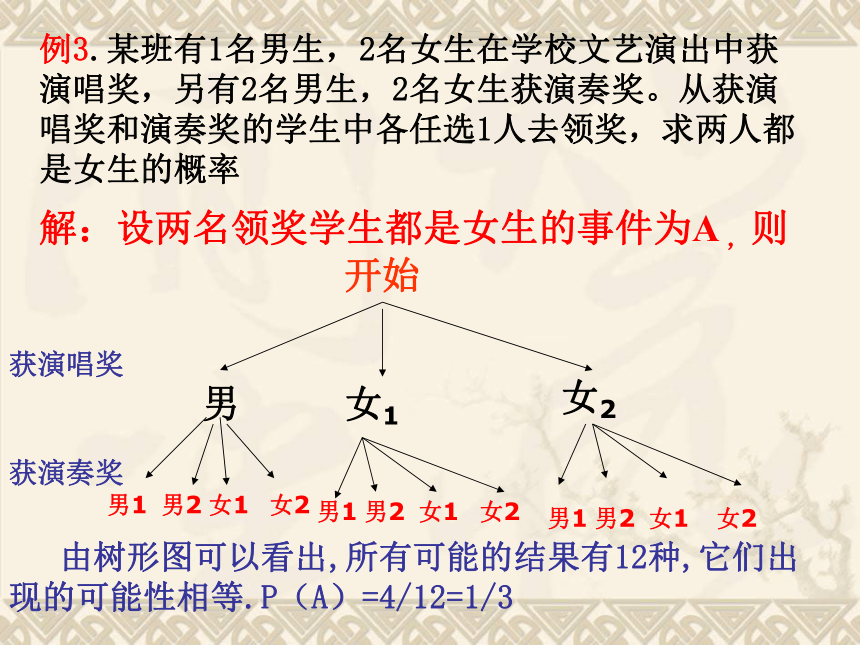
当试验在三步或三步以上时,用树形图法方便.开始男女1女2男1男2女1女2例3.某班有1名男生,2名女生在学校文艺演出中获演唱奖,另有2名男生,2名女生获演奏奖。从获演唱奖和演奏奖的学生中各任选1人去领奖,求两人都是女生的概率男1男2女1女2男1男2女1女2获演唱奖获演奏奖解:设两名领奖学生都是女生的事件为A ,则 由树形图可以看出,所有可能的结果有12种,它们出现的可能性相等.P(A)=4/12=1/3练习 1.用数字1、2、3,组成三位数,求其中恰有2个相同的数字的概率.解: 由树形图可以看出,所有可能的结果有27种,它们出现的可能性相等.其中恰有2个数字相同的结果有18个.∴ P(恰有两个数字相同)=2.经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,如果这三种可能性大小相同,当有三辆汽车经过这个十字路口时,求下列事件的概率:(1)三辆车全部继续直行;(2)两辆车向右转,一辆车向左转;(3)至少有两辆车向左转.练习第
一
辆左右左右左直右第
二
辆第
三
辆直直左右直左右直左直右左直右左直右左直右左直右左直右左直右左直右解:画树形图如下:(1)三辆车全部继续直行(2)两辆车向右转,一辆车向左转(3)至少有两辆车向左转. 3.一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出一个球,记录下颜色后放回袋中并搅匀,再从中任意摸出一个球,两次都摸出红球的概率是多少?12练习结果第一次第二次解:利用表格列出所有可能的结果:红白红1红2白红1红2(白,白)(白,红1)(白,红2)(红1,白)(红1,红1)(红1,红2)(红2,白)(红2,红1)(红2,红2) 3.一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出一个球,记录下颜色后放回袋中并搅匀,再从中任意摸出一个球,两次都摸出红球的概率是多少? 一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出一个球,记录下颜色后不再放回袋中,再从中任意摸出一个球,两次都摸出红球的概率是多少?结果第一次第二次解:利用表格列出所有可能的结果:红变式白红1红2白红1红2(白,红1)(白,红2)(红1,白)(红1,红2)(红2,白)(红2,红1) 例4. 同时抛掷两枚均匀的骰子,骰子各面上的点数朝上的点数分别是1,2,3,4,5,6.分别求出如下随即事件的概率。
(1)抛出的点数之和等于7;
(2)抛出的点数之和等于12甲结果乙123654165432(6,6)12解:利用表格列出所有可能的结果:(5,6)11(4,6)10(3,6)9(2,6)8(1,6)7(6,5)11(5,5)10(3,5)8(2,5)7(1,5)6(6,4)10(5,4)9(3,4)7(2,4)6(1,4)5(6,3)9(5,3)8(3,3)6(2,3)5(1,3)4(6,2)8(5,2)7(3,2)5(2,2)4(1,2)3(6,1)7(5,1)6(3,1)4(2,1)3(1,1)2(4,1)5(4,2)6(4,3)7(4,4)8(4,5)9 在6张卡片上分别写有1-6的整数,随机地抽取一张后放回,再随机地抽取一张,那么第二次取出的数字能够整除第一次取出的数字的概率是多少? 解:由列表得,两次抽取卡片后,可能出现的结果有36个,它们出现的可能性相等.
满足第一次取出的数字能够整除第二次取出的数字(记为事件A)的结果有14个,则
P(A)= =练习 有两双手套,形状、大小,完全相同,只有颜色不同。黑暗中,任意抽出两只配成一双的概率是多少?分析:假设两双手套的颜色分别为红黑,如下分析红1
黑1黑2红2红2红1黑1黑1黑1黑2黑2黑2红1红1红2红2P(配成一双)==练习: 一个盒子里装有4个只有颜色不同的球,其中3个红球,1个白球。从盒子里摸出一个球,记下颜色后放回,并搅匀,再摸出一个球。(3)摸出一个红球,一个白球的概率;(2)摸出2个红球的概率;第1次第2次(1)写出两次摸球的所有可能的结果; 一个盒子里装有4个只有颜色不同的球,其中3个红球,1个白球。从盒子里摸出一个球,记下颜色后 ,并搅匀,再摸出一个球。(3)摸出一个红球,一个白球的概率;(2)摸出2个红球的概率;不放回(1)写出两次摸球的所有可能的结果;变:1.一张圆桌旁有四个座位,A先坐在如图所示的座位上,B、C、D三人随机坐到其他三个座位上。求A与B不相邻而坐的概率为 .练一练2.一个袋中里有4个珠子,其中2个红色,2个蓝色,除颜色外其余特征均相同,若从这个袋中任取2个珠子,都是蓝色珠子的概率为多少?
解:由题意画出树状图:开始由树状图可以看出,所有可能出现的结果共有6个,都是蓝色珠子的结果有1个。故1.用列举法求概率的条件是:
(1)实验的结果是有限个(n)
(2)各种结果的可能性相等.小结:2.用列举法求概率的的公式是:
(二)复习 当一次试验要涉及两个因素,并且可能出现的结果数目较多时,为了不重不漏的列出所有可能的结果,通常采用列表法.两个因素所组合的所有可能情况,即n 在所有可能情况n中,再找到满足条件的事件的个数m,最后代入公式计算.一个因素所包含的可能情况 另一个因素所包含的可能情况列表法中表格构造特点:当一次试验中涉及3个因素或更多的因素时,怎么办?
当一次试验中涉及3个因素或更多的因素时,用列表法就不方便了.为了不重不漏地列出所有可能的结果,通常采用“树形图”.树形图树形图的画法:一个试验第一个因素第二个第三个 如一个试验中涉及3个因素,第一个因素中有2种可能情况;第二个因素中有3种可能的情况;第三个因素中有2种可能的情况,AB123123abababababab则其树形图如图.n=2×3×2=12数学病院用下图所示的转盘进行“配紫色”游戏,游戏者获胜的概率是多少?刘华的思考过程如下:随机转动两个转盘,所有可能出现的结果如下:
你认为她的想法对吗,为什么?总共有9种结果,每种结果出现的可能性相同,而能够 配成紫色的结果只有一种: (红,蓝),故游戏者获胜的概率为1∕9 。用树状图或列表法求概率时,各种结果出现的可能性务必相同。 用树状图和列表的方法求概率的前提是: 各种结果出现的可能性务必相同.注意:想一想(1) 列表法和树形图法的优点是什么?
(2)什么时候使用“列表法”方便?什么时候使用“树形图法”方便?利用树形图或表格可以清晰地表示出某个事件发生的所有可能出现的结果;从而较方便地求出某些事件发生的概率.
当试验包含两步时,列表法比较方便,当然,此时也可以用树形图法;
当试验在三步或三步以上时,用树形图法方便.开始男女1女2男1男2女1女2例3.某班有1名男生,2名女生在学校文艺演出中获演唱奖,另有2名男生,2名女生获演奏奖。从获演唱奖和演奏奖的学生中各任选1人去领奖,求两人都是女生的概率男1男2女1女2男1男2女1女2获演唱奖获演奏奖解:设两名领奖学生都是女生的事件为A ,则 由树形图可以看出,所有可能的结果有12种,它们出现的可能性相等.P(A)=4/12=1/3练习 1.用数字1、2、3,组成三位数,求其中恰有2个相同的数字的概率.解: 由树形图可以看出,所有可能的结果有27种,它们出现的可能性相等.其中恰有2个数字相同的结果有18个.∴ P(恰有两个数字相同)=2.经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,如果这三种可能性大小相同,当有三辆汽车经过这个十字路口时,求下列事件的概率:(1)三辆车全部继续直行;(2)两辆车向右转,一辆车向左转;(3)至少有两辆车向左转.练习第
一
辆左右左右左直右第
二
辆第
三
辆直直左右直左右直左直右左直右左直右左直右左直右左直右左直右左直右解:画树形图如下:(1)三辆车全部继续直行(2)两辆车向右转,一辆车向左转(3)至少有两辆车向左转. 3.一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出一个球,记录下颜色后放回袋中并搅匀,再从中任意摸出一个球,两次都摸出红球的概率是多少?12练习结果第一次第二次解:利用表格列出所有可能的结果:红白红1红2白红1红2(白,白)(白,红1)(白,红2)(红1,白)(红1,红1)(红1,红2)(红2,白)(红2,红1)(红2,红2) 3.一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出一个球,记录下颜色后放回袋中并搅匀,再从中任意摸出一个球,两次都摸出红球的概率是多少? 一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出一个球,记录下颜色后不再放回袋中,再从中任意摸出一个球,两次都摸出红球的概率是多少?结果第一次第二次解:利用表格列出所有可能的结果:红变式白红1红2白红1红2(白,红1)(白,红2)(红1,白)(红1,红2)(红2,白)(红2,红1) 例4. 同时抛掷两枚均匀的骰子,骰子各面上的点数朝上的点数分别是1,2,3,4,5,6.分别求出如下随即事件的概率。
(1)抛出的点数之和等于7;
(2)抛出的点数之和等于12甲结果乙123654165432(6,6)12解:利用表格列出所有可能的结果:(5,6)11(4,6)10(3,6)9(2,6)8(1,6)7(6,5)11(5,5)10(3,5)8(2,5)7(1,5)6(6,4)10(5,4)9(3,4)7(2,4)6(1,4)5(6,3)9(5,3)8(3,3)6(2,3)5(1,3)4(6,2)8(5,2)7(3,2)5(2,2)4(1,2)3(6,1)7(5,1)6(3,1)4(2,1)3(1,1)2(4,1)5(4,2)6(4,3)7(4,4)8(4,5)9 在6张卡片上分别写有1-6的整数,随机地抽取一张后放回,再随机地抽取一张,那么第二次取出的数字能够整除第一次取出的数字的概率是多少? 解:由列表得,两次抽取卡片后,可能出现的结果有36个,它们出现的可能性相等.
满足第一次取出的数字能够整除第二次取出的数字(记为事件A)的结果有14个,则
P(A)= =练习 有两双手套,形状、大小,完全相同,只有颜色不同。黑暗中,任意抽出两只配成一双的概率是多少?分析:假设两双手套的颜色分别为红黑,如下分析红1
黑1黑2红2红2红1黑1黑1黑1黑2黑2黑2红1红1红2红2P(配成一双)==练习: 一个盒子里装有4个只有颜色不同的球,其中3个红球,1个白球。从盒子里摸出一个球,记下颜色后放回,并搅匀,再摸出一个球。(3)摸出一个红球,一个白球的概率;(2)摸出2个红球的概率;第1次第2次(1)写出两次摸球的所有可能的结果; 一个盒子里装有4个只有颜色不同的球,其中3个红球,1个白球。从盒子里摸出一个球,记下颜色后 ,并搅匀,再摸出一个球。(3)摸出一个红球,一个白球的概率;(2)摸出2个红球的概率;不放回(1)写出两次摸球的所有可能的结果;变:1.一张圆桌旁有四个座位,A先坐在如图所示的座位上,B、C、D三人随机坐到其他三个座位上。求A与B不相邻而坐的概率为 .练一练2.一个袋中里有4个珠子,其中2个红色,2个蓝色,除颜色外其余特征均相同,若从这个袋中任取2个珠子,都是蓝色珠子的概率为多少?
解:由题意画出树状图:开始由树状图可以看出,所有可能出现的结果共有6个,都是蓝色珠子的结果有1个。故1.用列举法求概率的条件是:
(1)实验的结果是有限个(n)
(2)各种结果的可能性相等.小结:2.用列举法求概率的的公式是:
