沪科版九下27.2等可能情形下的概率(三) 课件
文档属性
| 名称 | 沪科版九下27.2等可能情形下的概率(三) 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 173.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-31 12:44:48 | ||
图片预览






文档简介
课件21张PPT。27.2等可能性事件的概率
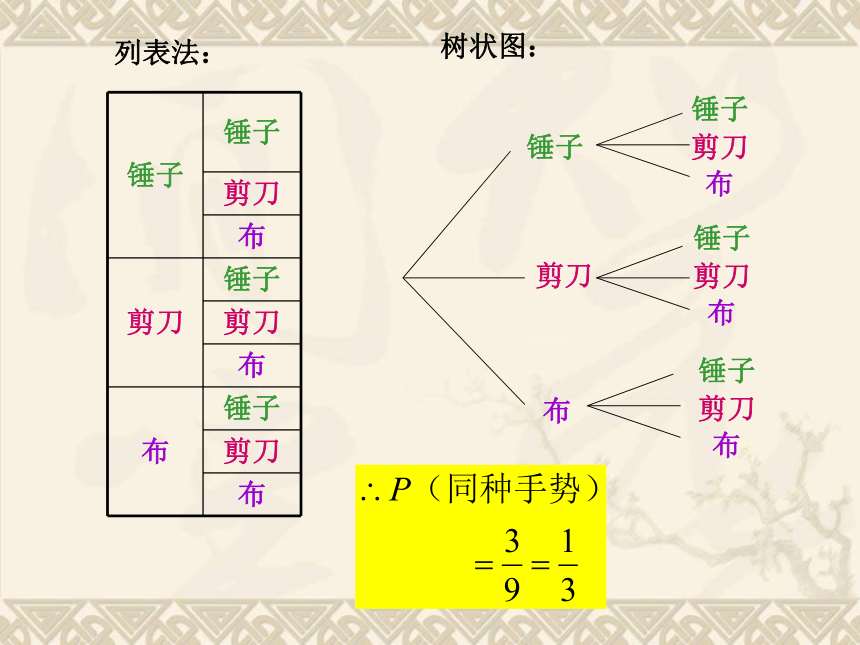
(三)例5: “石头、剪刀、布”是广为流传的游戏,游戏时甲乙双方每次做“石头” “剪刀”“布”三种手势中的一种,规定“石头” 胜“剪刀”, “剪刀”胜“布”, “布”胜“石头”,同种手势不分胜负须继续比赛。假定甲、乙两人每次都是等可能地做这三种手势,那么一次比赛时两人做同种手势(不分胜负)的概率是多少?3列表法:例6:一个密码锁的密码由三个数字组成,每个数字都是0-9这十个数字中的一个,只有当三个数字与所设定的密码相同时,才能将锁打开.粗心的小明忘了其中中间的两个数字,他一次就能打开该锁的概率是多少?解:其概率为1/1000.第一次从0-9这10个数字中抽取1个数字,其概率为1/10;第二次仍从0-9中抽取每二个数字,其概率仍为1/10.第三次仍从0-9中抽取每二个数字,其概率仍为1/10故概率为1/1000.甲:无论如何总是上开来的第一辆车,
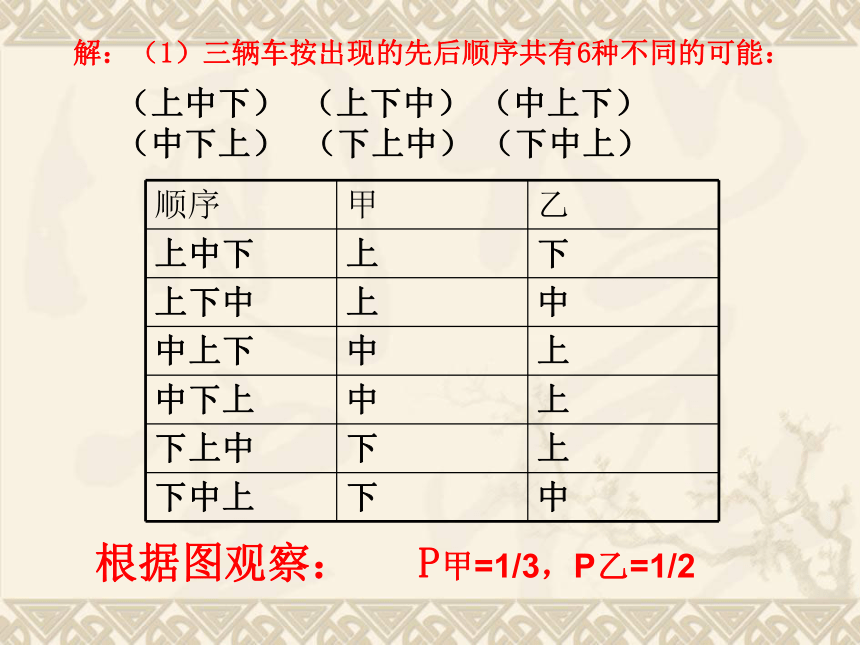
乙:先观察后上车,当第一辆车开来时,他不上车,而是仔细观察车的舒适状况,如果第二辆车的舒适程度比第一辆好,他就上第二辆车;如果第二辆车不比第一辆好,他就上第三辆车。例7:假设每天某一时段开往温州有三辆专车(票价相同),有两人相约来温州游玩,但是他们不知道这些车的舒适程度,也不知道专车开过来的顺序,两人采用了不同的乘车方案: 如果把这三辆车的舒适程度分为上、中、下三等,请尝试着解决下面的问题:(2)你认为甲、乙采用的方案,哪一种方案使自己乘上等车的可能性大?为什么?(1)三辆车按出现的先后顺序共有哪几种不同的可能?解:(1)三辆车按出现的先后顺序共有6种不同的可能:(上中下) (上下中) (中上下)
(中下上) (下上中) (下中上) 根据图观察: P甲=1/3,P乙=1/2
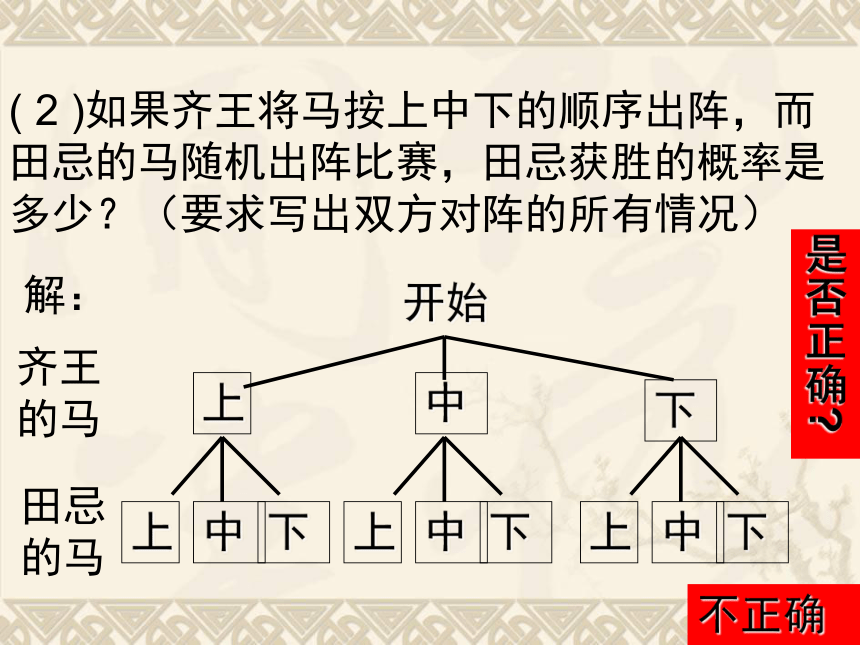
传说战国时期,齐王与田忌各有上、中、下三匹马,同等级的马中,齐王的马比田忌的马强.有一天,齐王要与田忌赛马,双方约定:比赛三局,每局各出一匹,每匹马赛一次,赢得两局者为胜.看样子田忌似乎没有什么胜的希望,但是田忌的谋士了解到主人的上、中等马分别比齐王的中、下等马要强 … … ( 1 )如果齐王将马按上中下的顺序出阵比赛,那么田忌的马如何出阵,田忌才能取胜? 田忌赛马( 2 )如果齐王将马按上中下的顺序出阵,而田忌的马随机出阵比赛,田忌获胜的概率是多少?(要求写出双方对阵的所有情况) 开始齐王
的马田忌
的马解:是否正确?不正确( 2 )如果齐王将马按上中下的顺序出阵,而田忌的马随机出阵比赛,田忌获胜的概率是多少?(要求写出双方对阵的所有情况) 双方的马对战中,只有一种情况田忌能赢,
所以田忌获胜的概率为 .试一试:
1、一个家庭有三个孩子,若一个孩子是男孩还是女孩的可能性相同.
(1)求这个家庭的3个孩子都是男孩的概率;
(2)求这个家庭有2个男孩和1个女孩的概率;
(3)求这个家庭至少有一个男孩的概率.解:(1)这个家庭的3个孩子都是男孩的概率为1/8;(2)这个家庭有2个男孩和1个女孩的概率为3/8;(3)这个家庭至少有一个男孩的概率为7/8.2、学校组织春游,安排九年级三辆车,小明与小慧都可以从这三辆车中任选一辆搭乘,问小明与小慧同车的概率有多大?丙解:记这三辆车分别为甲、乙、丙,小明与小慧乘车的所有可能的结果如下表:“配紫色”游戏小颖为学校联欢会设计了一个“配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分成相等的几个扇形.游戏规则是:游戏者同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,那么他就赢了,因为红色和蓝色在一起配成了紫色.(1)利用树状图或列表的方法表示游戏者所有可能出现的结果.
(2)游戏者获胜的概率是多少?
从上面的树状图可以看出,一次试验可能出现的结果共有6种,而且每种结果出现的可能性相同. 其中结果是(红,蓝)的有一种,所以游戏者获胜的概率是1/6.解:随意转动转盘,所有可能出现的结果如下: 从上面的表格可以看出,一次试验可能出现的结果共有6种,而且每种结果出现的可能性相同. 其中结果是(红,蓝)的有一种,所以游戏者获胜的概率是1/6.黄蓝绿红(红,黄)(红,蓝)(红,绿)白(白,黄)(白,蓝)(白,绿)解:随意转动转盘,所有可能出现的结果如下: 用如图所示的转盘进行“配紫色”游戏. 小颖制作了下图,并据此求出游戏者获胜的 概率是1/2.“配紫色”游戏的变异对此你有什么评论?“配紫色”游戏的变异小亮则先把左边转盘的红色区域等分成2份,分别记作“红色1”,“红色2”,然后制作了下表,据此求出游戏者获胜的概率也是1/2. 你认为谁做的对?说说你的理由.由“配紫色”游戏的变异想到的小颖的做法不正确.因为左边的转盘中红色部分和蓝色部分的面积不相同,因而指针落在这两个区域的可能性不同.
小亮的做法是解决这类问题的一种常用方法.用树状图和列表的方法求概率时应注意些什么? 用树状图和列表的方法求概率时应注意各种结果出现的可能性务必相同. 如图,袋中装有两个完全相同的球,分别标有数字“1”和“2”.小明设计了一个游戏:游戏者每次从袋中随机摸出一个球,并自由转动图中的转盘(转盘被分成相等的三个扇形).游戏规则是:
如果所摸球上的数字与转盘转出的数字之和为2,那么游戏者获胜.求游戏者获胜的概率.用心领“悟”解:每次游戏时,所有可能出现的结果如下: 又表格可知总共有6种结果,每种结果出现的可能性相同,而所摸球上的数字与转盘转出的数字之和为2的结果只有一种:(1,1),因此游戏者获胜的概率为1/6.112(1,1)(1,2)2(2,1)(2,2)3(1,3)(2,3)解:每次游戏时,所有可能出现的结果如下: 由树状图可知总共有6种结果,每种结果出现的可能性相同,而所摸球上的数字与转盘转出的数字之和为2的结果只有一种:(1,1),因此游戏者获胜的概率为1/6.112(1,1)(1,2)2(2,1)(2,2)3(1,3)(2,3)开始123
(三)例5: “石头、剪刀、布”是广为流传的游戏,游戏时甲乙双方每次做“石头” “剪刀”“布”三种手势中的一种,规定“石头” 胜“剪刀”, “剪刀”胜“布”, “布”胜“石头”,同种手势不分胜负须继续比赛。假定甲、乙两人每次都是等可能地做这三种手势,那么一次比赛时两人做同种手势(不分胜负)的概率是多少?3列表法:例6:一个密码锁的密码由三个数字组成,每个数字都是0-9这十个数字中的一个,只有当三个数字与所设定的密码相同时,才能将锁打开.粗心的小明忘了其中中间的两个数字,他一次就能打开该锁的概率是多少?解:其概率为1/1000.第一次从0-9这10个数字中抽取1个数字,其概率为1/10;第二次仍从0-9中抽取每二个数字,其概率仍为1/10.第三次仍从0-9中抽取每二个数字,其概率仍为1/10故概率为1/1000.甲:无论如何总是上开来的第一辆车,
乙:先观察后上车,当第一辆车开来时,他不上车,而是仔细观察车的舒适状况,如果第二辆车的舒适程度比第一辆好,他就上第二辆车;如果第二辆车不比第一辆好,他就上第三辆车。例7:假设每天某一时段开往温州有三辆专车(票价相同),有两人相约来温州游玩,但是他们不知道这些车的舒适程度,也不知道专车开过来的顺序,两人采用了不同的乘车方案: 如果把这三辆车的舒适程度分为上、中、下三等,请尝试着解决下面的问题:(2)你认为甲、乙采用的方案,哪一种方案使自己乘上等车的可能性大?为什么?(1)三辆车按出现的先后顺序共有哪几种不同的可能?解:(1)三辆车按出现的先后顺序共有6种不同的可能:(上中下) (上下中) (中上下)
(中下上) (下上中) (下中上) 根据图观察: P甲=1/3,P乙=1/2
传说战国时期,齐王与田忌各有上、中、下三匹马,同等级的马中,齐王的马比田忌的马强.有一天,齐王要与田忌赛马,双方约定:比赛三局,每局各出一匹,每匹马赛一次,赢得两局者为胜.看样子田忌似乎没有什么胜的希望,但是田忌的谋士了解到主人的上、中等马分别比齐王的中、下等马要强 … … ( 1 )如果齐王将马按上中下的顺序出阵比赛,那么田忌的马如何出阵,田忌才能取胜? 田忌赛马( 2 )如果齐王将马按上中下的顺序出阵,而田忌的马随机出阵比赛,田忌获胜的概率是多少?(要求写出双方对阵的所有情况) 开始齐王
的马田忌
的马解:是否正确?不正确( 2 )如果齐王将马按上中下的顺序出阵,而田忌的马随机出阵比赛,田忌获胜的概率是多少?(要求写出双方对阵的所有情况) 双方的马对战中,只有一种情况田忌能赢,
所以田忌获胜的概率为 .试一试:
1、一个家庭有三个孩子,若一个孩子是男孩还是女孩的可能性相同.
(1)求这个家庭的3个孩子都是男孩的概率;
(2)求这个家庭有2个男孩和1个女孩的概率;
(3)求这个家庭至少有一个男孩的概率.解:(1)这个家庭的3个孩子都是男孩的概率为1/8;(2)这个家庭有2个男孩和1个女孩的概率为3/8;(3)这个家庭至少有一个男孩的概率为7/8.2、学校组织春游,安排九年级三辆车,小明与小慧都可以从这三辆车中任选一辆搭乘,问小明与小慧同车的概率有多大?丙解:记这三辆车分别为甲、乙、丙,小明与小慧乘车的所有可能的结果如下表:“配紫色”游戏小颖为学校联欢会设计了一个“配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分成相等的几个扇形.游戏规则是:游戏者同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,那么他就赢了,因为红色和蓝色在一起配成了紫色.(1)利用树状图或列表的方法表示游戏者所有可能出现的结果.
(2)游戏者获胜的概率是多少?
从上面的树状图可以看出,一次试验可能出现的结果共有6种,而且每种结果出现的可能性相同. 其中结果是(红,蓝)的有一种,所以游戏者获胜的概率是1/6.解:随意转动转盘,所有可能出现的结果如下: 从上面的表格可以看出,一次试验可能出现的结果共有6种,而且每种结果出现的可能性相同. 其中结果是(红,蓝)的有一种,所以游戏者获胜的概率是1/6.黄蓝绿红(红,黄)(红,蓝)(红,绿)白(白,黄)(白,蓝)(白,绿)解:随意转动转盘,所有可能出现的结果如下: 用如图所示的转盘进行“配紫色”游戏. 小颖制作了下图,并据此求出游戏者获胜的 概率是1/2.“配紫色”游戏的变异对此你有什么评论?“配紫色”游戏的变异小亮则先把左边转盘的红色区域等分成2份,分别记作“红色1”,“红色2”,然后制作了下表,据此求出游戏者获胜的概率也是1/2. 你认为谁做的对?说说你的理由.由“配紫色”游戏的变异想到的小颖的做法不正确.因为左边的转盘中红色部分和蓝色部分的面积不相同,因而指针落在这两个区域的可能性不同.
小亮的做法是解决这类问题的一种常用方法.用树状图和列表的方法求概率时应注意些什么? 用树状图和列表的方法求概率时应注意各种结果出现的可能性务必相同. 如图,袋中装有两个完全相同的球,分别标有数字“1”和“2”.小明设计了一个游戏:游戏者每次从袋中随机摸出一个球,并自由转动图中的转盘(转盘被分成相等的三个扇形).游戏规则是:
如果所摸球上的数字与转盘转出的数字之和为2,那么游戏者获胜.求游戏者获胜的概率.用心领“悟”解:每次游戏时,所有可能出现的结果如下: 又表格可知总共有6种结果,每种结果出现的可能性相同,而所摸球上的数字与转盘转出的数字之和为2的结果只有一种:(1,1),因此游戏者获胜的概率为1/6.112(1,1)(1,2)2(2,1)(2,2)3(1,3)(2,3)解:每次游戏时,所有可能出现的结果如下: 由树状图可知总共有6种结果,每种结果出现的可能性相同,而所摸球上的数字与转盘转出的数字之和为2的结果只有一种:(1,1),因此游戏者获胜的概率为1/6.112(1,1)(1,2)2(2,1)(2,2)3(1,3)(2,3)开始123
