沪科版九下27.2等可能情形下的概率(一) 课件
文档属性
| 名称 | 沪科版九下27.2等可能情形下的概率(一) 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 160.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-31 12:42:44 | ||
图片预览








文档简介
课件22张PPT。27.2等可能性事件的概率
(一)
会用画树状图的方法求简单事件的概率.
会用列表的方法求简单事件的概率.学习目标:复习引入 必然事件;
在一定条件下必然发生的事件,
不可能事件;
在一定条件下不可能发生的事件
随机事件;
在一定条件下可能发生也可能不发生的事件,概率的定义 0≤P(A) ≤1.
必然事件的概率是1,不可能事件的概率是0. 一般地,对于一个随机事件A,我们把刻画其发生可能性大小的数值,称为随机事件A的概率,记作P(A)。归纳:求随机事件A的概率的方法: 一般的,如果在一次试验中,有n种可能的结果,并且他们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率P(A)= 这节课我们将学习根据树状图理性和列表法分析预测概率有5张数字卡片,它们的背面完全相同,正面分别标有1,2,2,3,4。现将它们的背面朝上,从中任意摸到一张卡片,则:p (摸到2号卡片)= ;p (摸到奇数号卡片)= ; P(摸到偶数号卡片) = .p (摸到1号卡片)= ;
练习: 如图,由A村去B村的道路有三条,由B村去C村的道路有两条,(1)从A村经B村去C村有多少种不同的走法?(2)某人从中任选一条路线,选中“先经A—B中路,再经B—C南路”的概率是多少?(1)6种;
(2)1/6A村B村C村北南中北南练习: 例1:一只口袋中放着8只红球和16只黑球,这两种球除了颜色以外没有任何区别.袋中的球已经搅匀.蒙上眼睛从口袋中取一只球,取出黑球与红球的概率分别是多少?
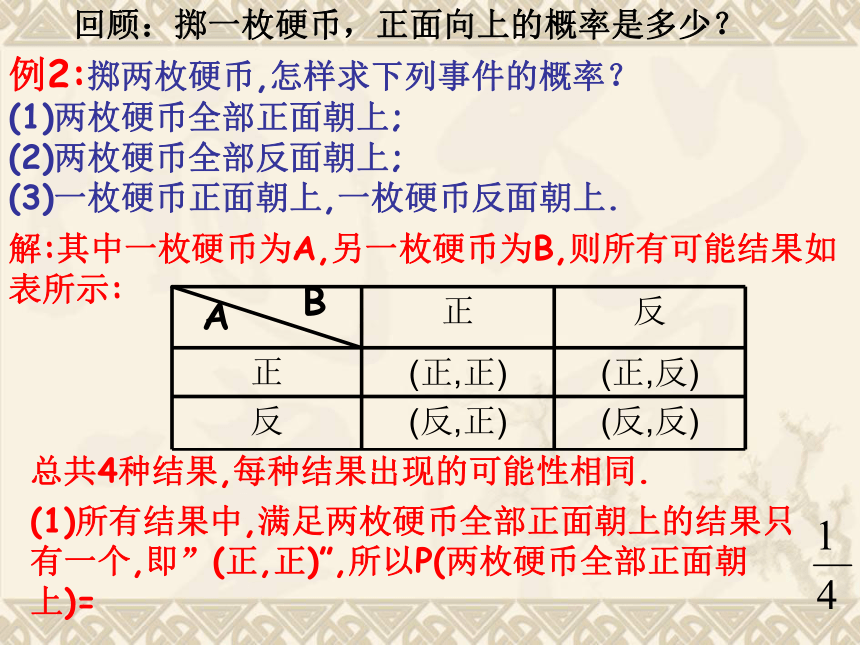
?解:P(取出黑球)= =P(取出红球)= 1-P(取出黑球)=所以取出黑球的概率是 取出红球的概率是 例2:掷两枚硬币,怎样求下列事件的概率?
(1)两枚硬币全部正面朝上;
(2)两枚硬币全部反面朝上;
(3)一枚硬币正面朝上,一枚硬币反面朝上.解:其中一枚硬币为A,另一枚硬币为B,则所有可能结果如表所示:AB总共4种结果,每种结果出现的可能性相同.(1)所有结果中,满足两枚硬币全部正面朝上的结果只有一个,即”(正,正)”,所以P(两枚硬币全部正面朝上)=回顾:掷一枚硬币,正面向上的概率是多少?(2)两枚硬币全部反面朝上;
(3)一枚硬币正面朝上,一枚硬币反面朝上.AB(2)所有结果中,满足两枚硬币全部反面朝上的结果只有一个,即”(反,反)”,所以P(两枚硬币全部反面朝上)=(3)所有结果中,满足一枚硬币正面朝上, 一枚硬币反面朝上的结果有2个,即”(正,反),(反,正)”,所以P(一枚硬币正面朝上,一枚硬币反面朝上)= 总共有4种结果:(正,正),(正,反),(反,正)(反,反)开始正反正反正反(正,正)(正,反)(反,正)(反,反)例2:掷两枚硬币,怎样求下列事件的概率?
(1)两枚硬币全部正面朝上;
(2)两枚硬币全部反面朝上;
(3)一枚硬币正面朝上,一枚硬币反面朝上.(1)P(两枚硬币全部正面朝上)=1/4,(2)P(两枚硬币全部反面朝上)=1/4,(3)P(一枚硬币正面朝上,一枚硬币反面朝上)=2/4
变式:有的同学认为:抛三枚普通硬币,硬币落地后只可能出现4种情况(1)全是正面;(2)两正一反;(3)两反一正;(4)全是反面。因些这四个事件出现的概率相等,你同意这种说法吗?解:画树状图分析如下开始硬币1正反硬币2硬币3正反正反正反正反正反正反1.随机掷一枚均匀的硬币两次,两次正面都朝上的概率是( ).
A. B. C. D.1.
2.从甲地到乙地可坐飞机、火车、汽车,从乙地到丙地可坐飞机、火车、汽车、轮船,某人乘坐以上交通工具,从甲地经乙地到丙地的方法有( )种.
A.4 B.7 C.12 D.81.一 精心选一选3从一个不透明的口袋里,摸出红球的概率为0.2,已知袋中有红球3个,则袋中小球的总个数是( )A.5 B. 8 C. 10 D.15.ACD4.设有12只型号相同的杯子,其中一等品7只,二等品3只,三等品2只.则从中任意取1只,是二等品的概率等于( ).
A. B. C. D.1.
5.一个均匀的正方体的六个面上分别标有数1,2,3,4,5,6.右图是这个正方体表面的展开图.抛掷这个正方体,则“朝上一面上的数恰好等于朝下一面上的数的一半”的概率是( ).
A. B. C. D.
CD6.中央电视台“幸运52”栏目中的“百宝箱”互动环节,是一种竞猜游戏,游戏规则如下:在20个商标中,有5个商标牌的背面注明了一定的奖金额,其余商标的背面是一张苦脸,若翻到它就不得奖。参加这个游戏的观众有三次翻牌的机会。某观众前两次翻牌均得若干奖金,如果翻过的牌不能再翻,那么这位观众第三次翻牌获奖的概率是( ).
A. B. C. D. A1. 有一对酷爱运动的年轻夫妇给他们12个月大的婴儿拼排3块分别写有“20”,“08"和“北京”的字块,如果婴儿能够排成"2008北京”或者“北京2008".则他们就给婴儿奖励,假设婴儿能将字块横着正排,那么这个婴儿能得到奖励的概率是___________.3、先后抛掷三枚均匀的硬币,至少出现一次正面的概率是二 大胆填一填2一个游戏的中奖率是1%,买100张奖券,一定会中奖吗?
1/37/8不一定你能用树状图表示吗?4、有100张卡片(从1号到100号),从中任取1张,取到的卡号是11的倍数的概率为5、某组16名学生,其中男女生各一半,把全组学生分成人数相等的两个小组,则分得每小组里男、女人数相同的概率是6.如图一个由大小相同的黑白小方块相间的长方形,若用一个小球在上面任意滚动,落在黑色方块内的概率是9/1001/47/18解:设两双袜子分别为A1、A2、B1、B2,则所以穿相同一双袜子的概率为1/31.小明是个小马虎,晚上睡觉时将两双不同的袜子放在床头,早上起床没看清随便穿了两只就去上学,问小明正好穿的是相同的一双袜子的概率是多少?练习: 2.甲口袋中装有2个相同的小球,它们分别写有字母A和B;乙口袋中装有3个相同的小球,它们分别写有字母C.D和E;丙口袋中装有2个相同的小球,它们分别写有字母H和I,从3个口袋中各随机地取出1个小球.(2)取出的3个小球上全是辅音字母的概率是多少?(1)取出的3个小球上,恰好有1个,2个和3个元音字母的概率分别是多少?练习:甲乙丙EDCEDC解:根据题意,我们可以画出如下的树形图
A A A A A A B B B B B B
C C D D E E C C D D E E
H I H I H I H I H I H I (1)只有一个元音字母(记为事件A)的结果有5个,所以 P(A)=根据树形图,可以看出,所有可能出现的结果是12个,这些结果出现的可能性相等,(2)只有两个元音字母(记为事件B)的结果有4个,所以 P(B)=(3)有三个元音字母(记为事件C)的结果有1个,所以 P(C)=5/121/31/12 利用树状图或表格可以清晰地表示出某个事件发生的所有可能出现的结果,从而较方便地求出某些事件发生的概率.当试验包含两步时,列表法法比较方便,当然,此时也可以用树状图法,当试验在三步或三步以上时,用树状图法方便.用列表法和树状图法求概率时应注意什么情况? 1.三种事件发生的概率及表示?2.等可能性事件的两个特征:(1)出现的结果有限多个;
(2)各结果发生的可能性相等;如何求等可能性事件的概率------- 树状图列表法课堂小结
(一)
会用画树状图的方法求简单事件的概率.
会用列表的方法求简单事件的概率.学习目标:复习引入 必然事件;
在一定条件下必然发生的事件,
不可能事件;
在一定条件下不可能发生的事件
随机事件;
在一定条件下可能发生也可能不发生的事件,概率的定义 0≤P(A) ≤1.
必然事件的概率是1,不可能事件的概率是0. 一般地,对于一个随机事件A,我们把刻画其发生可能性大小的数值,称为随机事件A的概率,记作P(A)。归纳:求随机事件A的概率的方法: 一般的,如果在一次试验中,有n种可能的结果,并且他们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率P(A)= 这节课我们将学习根据树状图理性和列表法分析预测概率有5张数字卡片,它们的背面完全相同,正面分别标有1,2,2,3,4。现将它们的背面朝上,从中任意摸到一张卡片,则:p (摸到2号卡片)= ;p (摸到奇数号卡片)= ; P(摸到偶数号卡片) = .p (摸到1号卡片)= ;
练习: 如图,由A村去B村的道路有三条,由B村去C村的道路有两条,(1)从A村经B村去C村有多少种不同的走法?(2)某人从中任选一条路线,选中“先经A—B中路,再经B—C南路”的概率是多少?(1)6种;
(2)1/6A村B村C村北南中北南练习: 例1:一只口袋中放着8只红球和16只黑球,这两种球除了颜色以外没有任何区别.袋中的球已经搅匀.蒙上眼睛从口袋中取一只球,取出黑球与红球的概率分别是多少?
?解:P(取出黑球)= =P(取出红球)= 1-P(取出黑球)=所以取出黑球的概率是 取出红球的概率是 例2:掷两枚硬币,怎样求下列事件的概率?
(1)两枚硬币全部正面朝上;
(2)两枚硬币全部反面朝上;
(3)一枚硬币正面朝上,一枚硬币反面朝上.解:其中一枚硬币为A,另一枚硬币为B,则所有可能结果如表所示:AB总共4种结果,每种结果出现的可能性相同.(1)所有结果中,满足两枚硬币全部正面朝上的结果只有一个,即”(正,正)”,所以P(两枚硬币全部正面朝上)=回顾:掷一枚硬币,正面向上的概率是多少?(2)两枚硬币全部反面朝上;
(3)一枚硬币正面朝上,一枚硬币反面朝上.AB(2)所有结果中,满足两枚硬币全部反面朝上的结果只有一个,即”(反,反)”,所以P(两枚硬币全部反面朝上)=(3)所有结果中,满足一枚硬币正面朝上, 一枚硬币反面朝上的结果有2个,即”(正,反),(反,正)”,所以P(一枚硬币正面朝上,一枚硬币反面朝上)= 总共有4种结果:(正,正),(正,反),(反,正)(反,反)开始正反正反正反(正,正)(正,反)(反,正)(反,反)例2:掷两枚硬币,怎样求下列事件的概率?
(1)两枚硬币全部正面朝上;
(2)两枚硬币全部反面朝上;
(3)一枚硬币正面朝上,一枚硬币反面朝上.(1)P(两枚硬币全部正面朝上)=1/4,(2)P(两枚硬币全部反面朝上)=1/4,(3)P(一枚硬币正面朝上,一枚硬币反面朝上)=2/4
变式:有的同学认为:抛三枚普通硬币,硬币落地后只可能出现4种情况(1)全是正面;(2)两正一反;(3)两反一正;(4)全是反面。因些这四个事件出现的概率相等,你同意这种说法吗?解:画树状图分析如下开始硬币1正反硬币2硬币3正反正反正反正反正反正反1.随机掷一枚均匀的硬币两次,两次正面都朝上的概率是( ).
A. B. C. D.1.
2.从甲地到乙地可坐飞机、火车、汽车,从乙地到丙地可坐飞机、火车、汽车、轮船,某人乘坐以上交通工具,从甲地经乙地到丙地的方法有( )种.
A.4 B.7 C.12 D.81.一 精心选一选3从一个不透明的口袋里,摸出红球的概率为0.2,已知袋中有红球3个,则袋中小球的总个数是( )A.5 B. 8 C. 10 D.15.ACD4.设有12只型号相同的杯子,其中一等品7只,二等品3只,三等品2只.则从中任意取1只,是二等品的概率等于( ).
A. B. C. D.1.
5.一个均匀的正方体的六个面上分别标有数1,2,3,4,5,6.右图是这个正方体表面的展开图.抛掷这个正方体,则“朝上一面上的数恰好等于朝下一面上的数的一半”的概率是( ).
A. B. C. D.
CD6.中央电视台“幸运52”栏目中的“百宝箱”互动环节,是一种竞猜游戏,游戏规则如下:在20个商标中,有5个商标牌的背面注明了一定的奖金额,其余商标的背面是一张苦脸,若翻到它就不得奖。参加这个游戏的观众有三次翻牌的机会。某观众前两次翻牌均得若干奖金,如果翻过的牌不能再翻,那么这位观众第三次翻牌获奖的概率是( ).
A. B. C. D. A1. 有一对酷爱运动的年轻夫妇给他们12个月大的婴儿拼排3块分别写有“20”,“08"和“北京”的字块,如果婴儿能够排成"2008北京”或者“北京2008".则他们就给婴儿奖励,假设婴儿能将字块横着正排,那么这个婴儿能得到奖励的概率是___________.3、先后抛掷三枚均匀的硬币,至少出现一次正面的概率是二 大胆填一填2一个游戏的中奖率是1%,买100张奖券,一定会中奖吗?
1/37/8不一定你能用树状图表示吗?4、有100张卡片(从1号到100号),从中任取1张,取到的卡号是11的倍数的概率为5、某组16名学生,其中男女生各一半,把全组学生分成人数相等的两个小组,则分得每小组里男、女人数相同的概率是6.如图一个由大小相同的黑白小方块相间的长方形,若用一个小球在上面任意滚动,落在黑色方块内的概率是9/1001/47/18解:设两双袜子分别为A1、A2、B1、B2,则所以穿相同一双袜子的概率为1/31.小明是个小马虎,晚上睡觉时将两双不同的袜子放在床头,早上起床没看清随便穿了两只就去上学,问小明正好穿的是相同的一双袜子的概率是多少?练习: 2.甲口袋中装有2个相同的小球,它们分别写有字母A和B;乙口袋中装有3个相同的小球,它们分别写有字母C.D和E;丙口袋中装有2个相同的小球,它们分别写有字母H和I,从3个口袋中各随机地取出1个小球.(2)取出的3个小球上全是辅音字母的概率是多少?(1)取出的3个小球上,恰好有1个,2个和3个元音字母的概率分别是多少?练习:甲乙丙EDCEDC解:根据题意,我们可以画出如下的树形图
A A A A A A B B B B B B
C C D D E E C C D D E E
H I H I H I H I H I H I (1)只有一个元音字母(记为事件A)的结果有5个,所以 P(A)=根据树形图,可以看出,所有可能出现的结果是12个,这些结果出现的可能性相等,(2)只有两个元音字母(记为事件B)的结果有4个,所以 P(B)=(3)有三个元音字母(记为事件C)的结果有1个,所以 P(C)=5/121/31/12 利用树状图或表格可以清晰地表示出某个事件发生的所有可能出现的结果,从而较方便地求出某些事件发生的概率.当试验包含两步时,列表法法比较方便,当然,此时也可以用树状图法,当试验在三步或三步以上时,用树状图法方便.用列表法和树状图法求概率时应注意什么情况? 1.三种事件发生的概率及表示?2.等可能性事件的两个特征:(1)出现的结果有限多个;
(2)各结果发生的可能性相等;如何求等可能性事件的概率------- 树状图列表法课堂小结
