沪科版九下27.3用频率估计概率 课件.
文档属性
| 名称 | 沪科版九下27.3用频率估计概率 课件. |

|
|
| 格式 | zip | ||
| 文件大小 | 219.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-31 13:05:47 | ||
图片预览





文档简介
课件24张PPT。27.3用频率估计概率2、用列举法求概率有哪几种?(1)实验的所有结果是有限个(n)
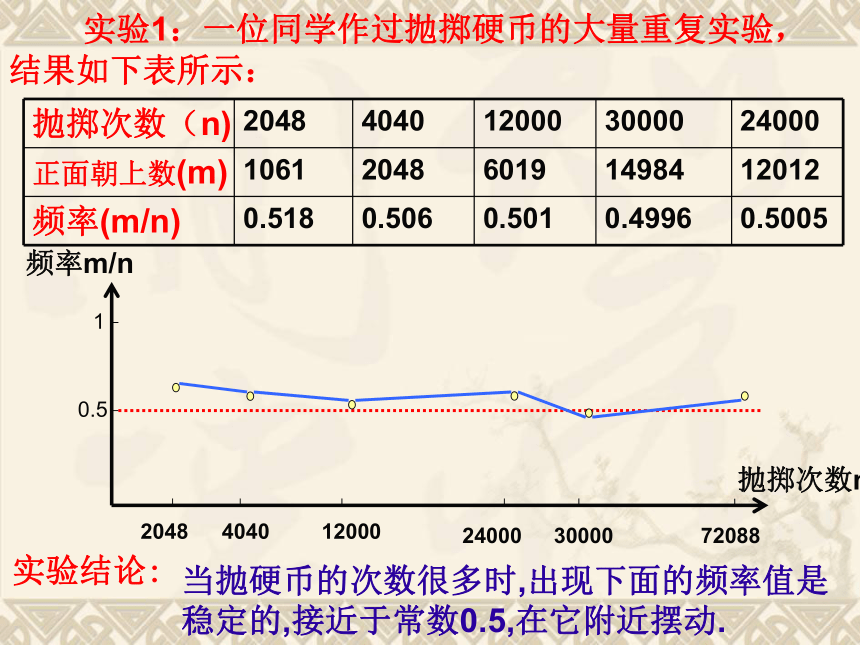
(2)各种结果的可能性相等. 当实验的所有结果不是有限个;或各种可能结果发生的可能性不相等时.又该如何求事件发生的概率呢?复习1、古典概率条件是什么?用什么方法求? 实验1:一位同学作过抛掷硬币的大量重复实验,结果如下表所示:实验结论:当抛硬币的次数很多时,出现下面的频率值是
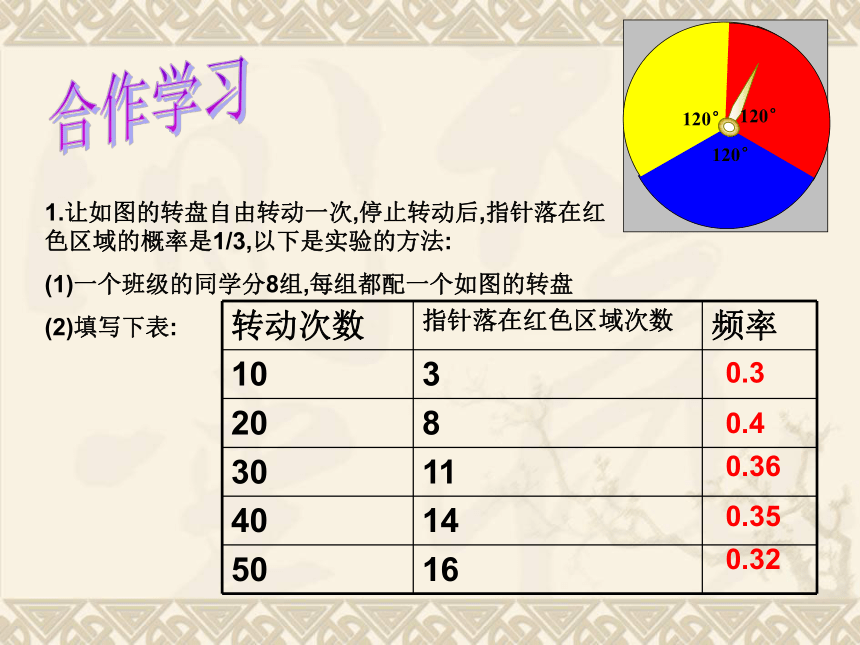
稳定的,接近于常数0.5,在它附近摆动. 我们知道,任意抛一枚均匀的硬币,”正面朝上”的概率是0.5,许多科学家曾做过成千上万次的实验,其中部分结果如下表:观察上表,你获得什么启示?实验次数越多,频率越接近概率实验2:某批乒乓球质量检查结果表实验3:某种油菜籽在相同条件下的发芽试验结果表 当抽查的球数很多时,抽到优等品的频率 接近于常数0.95,在它附近摆动。 很多常数 当试验的油菜籽的粒数很多时,油菜籽发芽的频率 接近于常数0.9,在它附近摆动。很多 常数合作学习1.让如图的转盘自由转动一次,停止转动后,指针落在红色区域的概率是1/3,以下是实验的方法:
(1)一个班级的同学分8组,每组都配一个如图的转盘
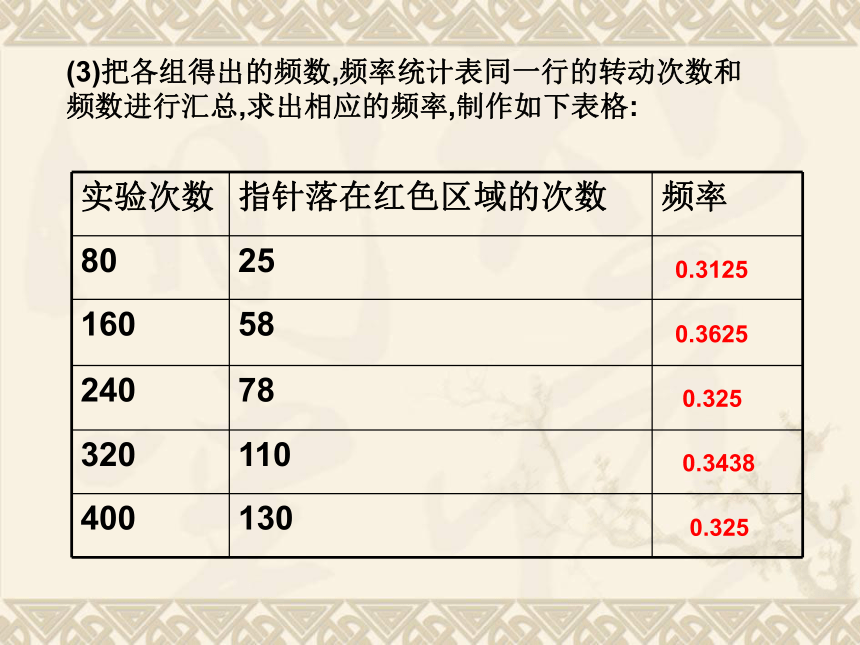
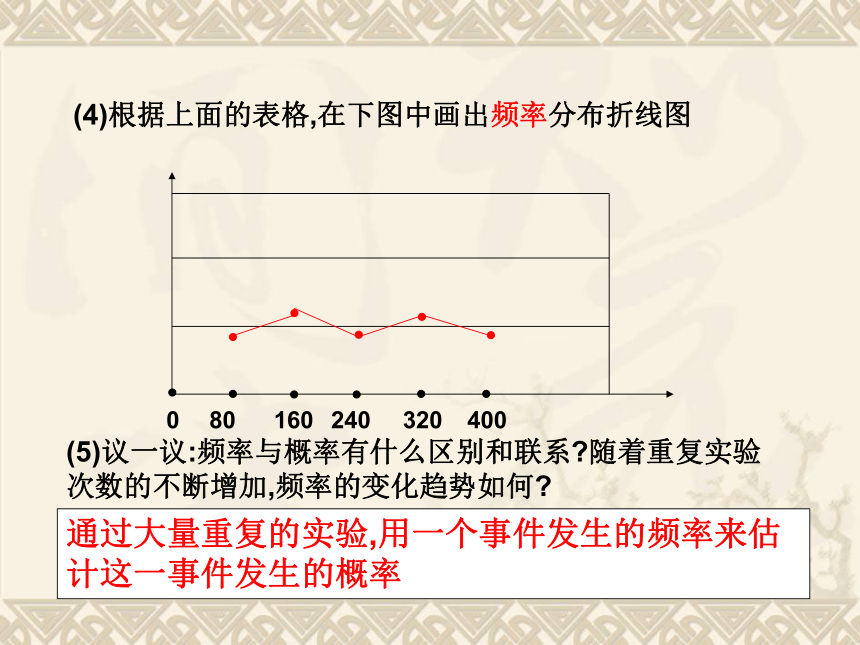
(2)填写下表:0.30.40.360.350.32(3)把各组得出的频数,频率统计表同一行的转动次数和频数进行汇总,求出相应的频率,制作如下表格:0.31250.36250.3250.34380.325(4)根据上面的表格,在下图中画出频率分布折线图(5)议一议:频率与概率有什么区别和联系?随着重复实验次数的不断增加,频率的变化趋势如何?400320240160800通过大量重复的实验,用一个事件发生的频率来估计这一事件发生的概率 2. 张小明承包了一片荒山,他想把这片荒山改造成一个苹果果园,现在有两批幼苗可以选择,它们的成活率如下两个表格所示: A类树苗: B类树苗:0.8
0.94
0.870
0.923
0.883
0.890
0.915
0.905
0.9020.9
0.98
0.85
0.9
0.855
0.850
0.856
0.855
0.851观察图表,回答问题串1、从表中可以发现,A类幼树移植成活的频率在_____左右摆动,并且随着统计数据的增加,这种规律愈加明显,估计A类幼树移植成活的概率为____,估计B类幼树移植成活的概率为___. 2、张小明选择A类树苗,还是B类树苗呢?_____,若他的荒山需要10000株树苗,则他实际需要进树苗________株? 3、如果每株树苗9元,则小明买树苗共需 ________元.0.90.90.85A类11112100008议一议: 从上面的实验可以看出,当重复实验的次数大量增加时,事件发生的频率就稳定在相应的概率附近 瑞士数学家雅各布.伯努利(1654-1705)最早阐明了可以由频率估计概率即: 在相同的条件下,大量的重复实验时,根据一个随机事件发生的频率所逐渐稳定的常数,可以估计这个事件发生的概率 频率与概率有什么区别和联系?随着重复实验次数的不断增加,频率的变化趋势如何? 大量的实验表明:当重复实验的次数大量增加时,事件发生的频数就稳定在相应的概率附近,因此,我们可以通过大量重复实验,用一个事件发生的频率来估计这一事件发生的概率 因此,我们一般把实验次数最多的频率近似作为该事件的概率共同归纳例题分析例1.在同样条件下对某种小麦种子进行发芽实验,统计发芽种子数,获得如下频数分布表:(1)计算表中各个频数.
(2)估计该麦种的发芽概率0.80.950.950.950.9510.9520.940.920.9(3)如果播种该种小麦每公顷所需麦苗数为4181818棵,种子发芽后的成秧率为87%,该麦种的千粒质量为35g,那么播种3公顷该种小麦,估计约需麦种多少kg?解:设需麦种x(kg)则粒数为 由题意得,解得 x≈531(kg)
答:播种3公顷该种小麦,估计约需531kg麦种. 例2:某水果公司以2元/千克的成本新进了10 000千克的柑橘,如果公司希望这些柑橘能够获得利润5 000元,那么在出售柑橘(已去掉损坏的柑橘)时,每千克大约定价为多少元比较合适? 销售人员首先从所有的柑橘中随机地抽取若干柑橘,进行了“柑橘损坏率”统计,并把获得的数据记录在表中,请你帮忙完成此表.并思考如果你是柑橘销售商,在整个销售过程中应注意些什么?
0.1010.0970.1030.1010.0980.0990.1030.097 从表可以看出,柑橘损坏的频率在常数_____左右摆动,并且随统计量的增加这种规律逐渐______,那么可以把柑橘损坏的概率估计为这个常数.如果估计这个概率为0.1,则柑橘完好的概率为_______.0.1稳定0.9根据估计的概率可以知道,在10000千克柑橘中,完好柑橘的质量为10000 X 0.9=9000千克完好柑橘的实际成本为
2 X 100009000≈ 2.22(元/千克)设每千克柑橘的销价为x元,则有( X—2.22 ) X 9000=5000解得 x ≈2.8因此,出售柑橘时每千克大约定价为2.8元可获利润5000元。
课堂小结: 频率不等于概率,但通过大量的重复实验,事件发生的频率值将逐渐稳定在相应的概率附近,此时的频率值可用于估计这一事件发生的概率 概率只表示事件发生的可能性的大小,不能说明某种肯定的结果。 概率是理论性规律的东西,频率是实践性的东西,理论应该联系实际,因此我们可以通过大量重复的实验,用一个事件发生的频率来估计这一事件发生的概率升华提高了解了一种方法-------用多次试验频率去估计概率体会了一种思想:用样本去估计总体
用频率去估计概率弄清了一种关系------频率与概率的关系 当试验次数很多或试验时样本容量足够大时,一件事件发生的频率与相应的概率会非常接近.此时,我们可以用一件事件发生的频率来估计这一事件发生的概率.做一做1.某运动员投篮5次,投中4次,能否说该运动员投一次篮,投中的概率为4/5?为什么?2、抽检1000件衬衣,其中不合格的衬衣有2件,由此估计抽1件衬衣合格的概率是多少?P=499/500P=1/10000000不能,因为只有当重复实验次数大量增加时,事件发生的频率才稳定在概率附近。3、1998年,在美国密歇根州汉诺城市的一个农场里出生了1头白色的小奶牛,据统计,平均出生1千万头牛才会有1头是白色的,由此估计出生一头奶牛为白色的概率为多少?试一试1.一水塘里有鲤鱼、鲫鱼、鲢鱼共1 000尾,一渔民通过多次捕获实验后发现:鲤鱼、鲫鱼出现的频率是31%和42%,则这个水塘里有鲤鱼_______尾,鲢鱼_______尾.310270 2.在有一个10万人的小镇,随机调查了2000人,其中有250人看中央电视台的早间新闻.在该镇随便问一个人,他看早间新闻的概率大约是多少?该镇看中央电视台早间新闻的大约是多少人?解:
根据概率的意义,可以认为其概率大约等于250/2000=0.125.
该镇约有100000×0.125=12500人看中央电视台的早间新闻. 小红和小明在操场上做游戏,他们先在地上画了半径分别为2m和3m的同心圆(如图),蒙上眼在一定距离外向圈内掷小石子,掷中阴影小红胜,掷中里面小圈小明胜,未掷入大圈内不算,你认为游戏公平吗?为什么?游戏公平吗?知识应用 如图,长方形内有一不规则区域,现在玩投掷游戏,如果随机掷中长方形的300次中,有150次是落在不规则图形内.(1)你能估计出掷中不规则图形的概率吗?(2)若该长方形的面积为150平方米,试估计不规则图形的面积.
(2)各种结果的可能性相等. 当实验的所有结果不是有限个;或各种可能结果发生的可能性不相等时.又该如何求事件发生的概率呢?复习1、古典概率条件是什么?用什么方法求? 实验1:一位同学作过抛掷硬币的大量重复实验,结果如下表所示:实验结论:当抛硬币的次数很多时,出现下面的频率值是
稳定的,接近于常数0.5,在它附近摆动. 我们知道,任意抛一枚均匀的硬币,”正面朝上”的概率是0.5,许多科学家曾做过成千上万次的实验,其中部分结果如下表:观察上表,你获得什么启示?实验次数越多,频率越接近概率实验2:某批乒乓球质量检查结果表实验3:某种油菜籽在相同条件下的发芽试验结果表 当抽查的球数很多时,抽到优等品的频率 接近于常数0.95,在它附近摆动。 很多常数 当试验的油菜籽的粒数很多时,油菜籽发芽的频率 接近于常数0.9,在它附近摆动。很多 常数合作学习1.让如图的转盘自由转动一次,停止转动后,指针落在红色区域的概率是1/3,以下是实验的方法:
(1)一个班级的同学分8组,每组都配一个如图的转盘
(2)填写下表:0.30.40.360.350.32(3)把各组得出的频数,频率统计表同一行的转动次数和频数进行汇总,求出相应的频率,制作如下表格:0.31250.36250.3250.34380.325(4)根据上面的表格,在下图中画出频率分布折线图(5)议一议:频率与概率有什么区别和联系?随着重复实验次数的不断增加,频率的变化趋势如何?400320240160800通过大量重复的实验,用一个事件发生的频率来估计这一事件发生的概率 2. 张小明承包了一片荒山,他想把这片荒山改造成一个苹果果园,现在有两批幼苗可以选择,它们的成活率如下两个表格所示: A类树苗: B类树苗:0.8
0.94
0.870
0.923
0.883
0.890
0.915
0.905
0.9020.9
0.98
0.85
0.9
0.855
0.850
0.856
0.855
0.851观察图表,回答问题串1、从表中可以发现,A类幼树移植成活的频率在_____左右摆动,并且随着统计数据的增加,这种规律愈加明显,估计A类幼树移植成活的概率为____,估计B类幼树移植成活的概率为___. 2、张小明选择A类树苗,还是B类树苗呢?_____,若他的荒山需要10000株树苗,则他实际需要进树苗________株? 3、如果每株树苗9元,则小明买树苗共需 ________元.0.90.90.85A类11112100008议一议: 从上面的实验可以看出,当重复实验的次数大量增加时,事件发生的频率就稳定在相应的概率附近 瑞士数学家雅各布.伯努利(1654-1705)最早阐明了可以由频率估计概率即: 在相同的条件下,大量的重复实验时,根据一个随机事件发生的频率所逐渐稳定的常数,可以估计这个事件发生的概率 频率与概率有什么区别和联系?随着重复实验次数的不断增加,频率的变化趋势如何? 大量的实验表明:当重复实验的次数大量增加时,事件发生的频数就稳定在相应的概率附近,因此,我们可以通过大量重复实验,用一个事件发生的频率来估计这一事件发生的概率 因此,我们一般把实验次数最多的频率近似作为该事件的概率共同归纳例题分析例1.在同样条件下对某种小麦种子进行发芽实验,统计发芽种子数,获得如下频数分布表:(1)计算表中各个频数.
(2)估计该麦种的发芽概率0.80.950.950.950.9510.9520.940.920.9(3)如果播种该种小麦每公顷所需麦苗数为4181818棵,种子发芽后的成秧率为87%,该麦种的千粒质量为35g,那么播种3公顷该种小麦,估计约需麦种多少kg?解:设需麦种x(kg)则粒数为 由题意得,解得 x≈531(kg)
答:播种3公顷该种小麦,估计约需531kg麦种. 例2:某水果公司以2元/千克的成本新进了10 000千克的柑橘,如果公司希望这些柑橘能够获得利润5 000元,那么在出售柑橘(已去掉损坏的柑橘)时,每千克大约定价为多少元比较合适? 销售人员首先从所有的柑橘中随机地抽取若干柑橘,进行了“柑橘损坏率”统计,并把获得的数据记录在表中,请你帮忙完成此表.并思考如果你是柑橘销售商,在整个销售过程中应注意些什么?
0.1010.0970.1030.1010.0980.0990.1030.097 从表可以看出,柑橘损坏的频率在常数_____左右摆动,并且随统计量的增加这种规律逐渐______,那么可以把柑橘损坏的概率估计为这个常数.如果估计这个概率为0.1,则柑橘完好的概率为_______.0.1稳定0.9根据估计的概率可以知道,在10000千克柑橘中,完好柑橘的质量为10000 X 0.9=9000千克完好柑橘的实际成本为
2 X 100009000≈ 2.22(元/千克)设每千克柑橘的销价为x元,则有( X—2.22 ) X 9000=5000解得 x ≈2.8因此,出售柑橘时每千克大约定价为2.8元可获利润5000元。
课堂小结: 频率不等于概率,但通过大量的重复实验,事件发生的频率值将逐渐稳定在相应的概率附近,此时的频率值可用于估计这一事件发生的概率 概率只表示事件发生的可能性的大小,不能说明某种肯定的结果。 概率是理论性规律的东西,频率是实践性的东西,理论应该联系实际,因此我们可以通过大量重复的实验,用一个事件发生的频率来估计这一事件发生的概率升华提高了解了一种方法-------用多次试验频率去估计概率体会了一种思想:用样本去估计总体
用频率去估计概率弄清了一种关系------频率与概率的关系 当试验次数很多或试验时样本容量足够大时,一件事件发生的频率与相应的概率会非常接近.此时,我们可以用一件事件发生的频率来估计这一事件发生的概率.做一做1.某运动员投篮5次,投中4次,能否说该运动员投一次篮,投中的概率为4/5?为什么?2、抽检1000件衬衣,其中不合格的衬衣有2件,由此估计抽1件衬衣合格的概率是多少?P=499/500P=1/10000000不能,因为只有当重复实验次数大量增加时,事件发生的频率才稳定在概率附近。3、1998年,在美国密歇根州汉诺城市的一个农场里出生了1头白色的小奶牛,据统计,平均出生1千万头牛才会有1头是白色的,由此估计出生一头奶牛为白色的概率为多少?试一试1.一水塘里有鲤鱼、鲫鱼、鲢鱼共1 000尾,一渔民通过多次捕获实验后发现:鲤鱼、鲫鱼出现的频率是31%和42%,则这个水塘里有鲤鱼_______尾,鲢鱼_______尾.310270 2.在有一个10万人的小镇,随机调查了2000人,其中有250人看中央电视台的早间新闻.在该镇随便问一个人,他看早间新闻的概率大约是多少?该镇看中央电视台早间新闻的大约是多少人?解:
根据概率的意义,可以认为其概率大约等于250/2000=0.125.
该镇约有100000×0.125=12500人看中央电视台的早间新闻. 小红和小明在操场上做游戏,他们先在地上画了半径分别为2m和3m的同心圆(如图),蒙上眼在一定距离外向圈内掷小石子,掷中阴影小红胜,掷中里面小圈小明胜,未掷入大圈内不算,你认为游戏公平吗?为什么?游戏公平吗?知识应用 如图,长方形内有一不规则区域,现在玩投掷游戏,如果随机掷中长方形的300次中,有150次是落在不规则图形内.(1)你能估计出掷中不规则图形的概率吗?(2)若该长方形的面积为150平方米,试估计不规则图形的面积.
