六年级下册数学苏教版4.4 解比例 课件 (共17张PPT)
文档属性
| 名称 | 六年级下册数学苏教版4.4 解比例 课件 (共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-05 13:34:40 | ||
图片预览






文档简介
(共17张PPT)
比 例
解比例
复习回顾
应用比例的基本性质,判断下面哪几组的两个比可以组成比例,把组成的比例写出来。
(1)14∶21和6∶9 (2)
(3)9∶12和12∶16 (4)1.4∶2和7∶10
21×6=14×9
14∶21=6∶9
12×12=9×16
9∶12=12∶16
2×7=1.4×10
1.4∶2=7∶10
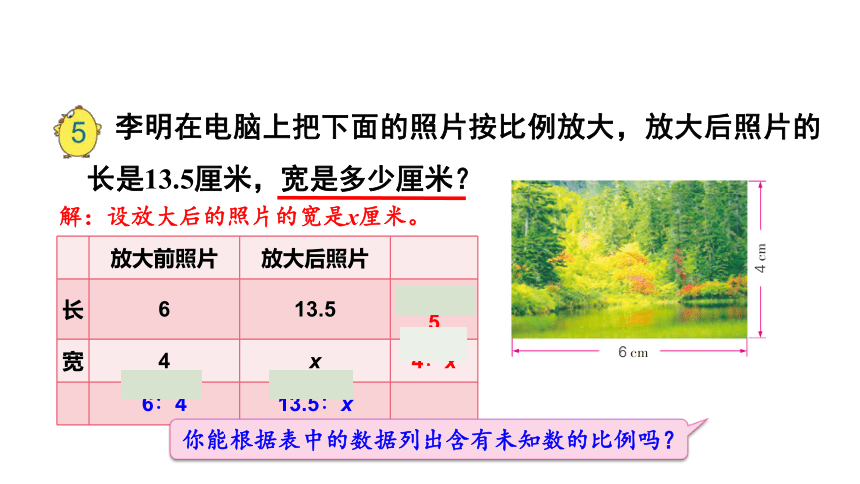
李明在电脑上把下面的照片按比例放大,放大后照片的长是13.5厘米,宽是多少厘米?
你是怎样理解“按比例放大”的?
两张照片长与宽的比能组成比例吗?为什么?
探究新知
李明在电脑上把下面的照片按比例放大,放大后照片的长是13.5厘米,宽是多少厘米?
解:设放大后的照片的宽是x厘米。
放大前照片 放大后照片
长 6 13.5 6∶13.5
宽 4 x 4∶x
6∶4 13.5∶x
你能根据表中的数据列出含有未知数的比例吗?
怎样求比例中的未知项?
放大前照片 放大后照片
长 6 13.5 6∶13.5
宽 4 x 4∶x
6∶4 13.5∶x
解:设放大后的照片的宽是x厘米。
6∶4=13.5∶x
解方程第一步的依据是什么?
6x=4×13.5
(在比例里,两个外项的积等于两个内项的积。)
6x=54
x=9
答:放大后照片的宽是9厘米。
还有其他的解题方法吗?
放大前照片 放大后照片
长 6 13.5 6∶13.5
宽 4 x 4∶x
6∶4 13.5∶x
解:设放大后的照片的宽是x厘米。
6∶13.5=4∶x
6x=4×13.5
(在比例里,两个外项的积等于两个内项的积。)
6x=54
x=9
答:放大后照片的宽是9厘米。
像上面这样求比例中的未知项,叫作解比例。
已知比例中的任意三项,就可以求出另外一项。
解比例的一般步骤:
(1)根据比例的基本性质,把比例转化成两个外项的积和两个内项的积相等的形式;
(2)通过解方程求出未知项的值。
归
纳
解比例
解: 1.2x=75×0.4
1.2x=30
x=25
1.找准比例式的外项和内项。
2.改写时可直接写成x在等式左边的形式。
【选自教材P40 试一试】
课堂练习
解比例。
9∶x=3∶4
解:3x=36
x=12
解:
解:0.1x=100×0.01
0.1x=1
x=10
【选自教材P40 练一练】
1.学校航模组有男生18人,女生15人;美术组有男生24人,女生20人。
(1)航模组男、女生人数的比和美术组男、女生人数的比能组成比例吗?
(2)如果能组成比例,指出比例的内项和外项。
【选自教材P41 练习七 第3题】
航模组 美术组
男生 18 24
女生 15 20
18∶15=24∶20
能组成比例。
外项
内项
8.小丽调制了两杯蜂蜜水,第一杯用了25毫升蜂蜜和200毫升水,第二杯用了30毫升蜂蜜和250毫升水。
(1)分别写出两杯蜂蜜水中蜂蜜与水体积的比,看看它们能否组成比例。
(2)按照第一杯蜂蜜水中蜂蜜与水体积的比计算,300毫升水中应加入蜂蜜多少毫升?
第一杯 第二杯
蜂蜜 25 30
水 200 250
不能
【选自教材P42 练习七 第8题】
第一杯 第三杯
蜂蜜 25 x
水 200 300
解:设300毫升水中应该加入x毫升蜂蜜。
25∶200=x∶300
200x=300×25
200x=7500
x=37.5
答:300毫升水中应该加入37.5毫升蜂蜜。
9.学校合唱组男生与女生的人数比是3∶4,合唱组男生有24人,女生有多少人?(你会用不同的方法解答吗?)
方法一:
24÷3=8(人)
4×8=32(人)
方法二:
设女生有x人。
3∶4=24∶x
3x=24×4
3x=96
x=32
答:女生有32人。
【选自教材P42 练习七 第9题】
如果 (m、n都不等于0),那么:
m∶n=( )∶( ), 。
解比例的一般步骤:
(1)根据比例的基本性质,把比例转化成两个外项的积和两个内项的积相等的形式;
(2)通过解方程求出未知项的值。
课堂小结
比 例
解比例
复习回顾
应用比例的基本性质,判断下面哪几组的两个比可以组成比例,把组成的比例写出来。
(1)14∶21和6∶9 (2)
(3)9∶12和12∶16 (4)1.4∶2和7∶10
21×6=14×9
14∶21=6∶9
12×12=9×16
9∶12=12∶16
2×7=1.4×10
1.4∶2=7∶10
李明在电脑上把下面的照片按比例放大,放大后照片的长是13.5厘米,宽是多少厘米?
你是怎样理解“按比例放大”的?
两张照片长与宽的比能组成比例吗?为什么?
探究新知
李明在电脑上把下面的照片按比例放大,放大后照片的长是13.5厘米,宽是多少厘米?
解:设放大后的照片的宽是x厘米。
放大前照片 放大后照片
长 6 13.5 6∶13.5
宽 4 x 4∶x
6∶4 13.5∶x
你能根据表中的数据列出含有未知数的比例吗?
怎样求比例中的未知项?
放大前照片 放大后照片
长 6 13.5 6∶13.5
宽 4 x 4∶x
6∶4 13.5∶x
解:设放大后的照片的宽是x厘米。
6∶4=13.5∶x
解方程第一步的依据是什么?
6x=4×13.5
(在比例里,两个外项的积等于两个内项的积。)
6x=54
x=9
答:放大后照片的宽是9厘米。
还有其他的解题方法吗?
放大前照片 放大后照片
长 6 13.5 6∶13.5
宽 4 x 4∶x
6∶4 13.5∶x
解:设放大后的照片的宽是x厘米。
6∶13.5=4∶x
6x=4×13.5
(在比例里,两个外项的积等于两个内项的积。)
6x=54
x=9
答:放大后照片的宽是9厘米。
像上面这样求比例中的未知项,叫作解比例。
已知比例中的任意三项,就可以求出另外一项。
解比例的一般步骤:
(1)根据比例的基本性质,把比例转化成两个外项的积和两个内项的积相等的形式;
(2)通过解方程求出未知项的值。
归
纳
解比例
解: 1.2x=75×0.4
1.2x=30
x=25
1.找准比例式的外项和内项。
2.改写时可直接写成x在等式左边的形式。
【选自教材P40 试一试】
课堂练习
解比例。
9∶x=3∶4
解:3x=36
x=12
解:
解:0.1x=100×0.01
0.1x=1
x=10
【选自教材P40 练一练】
1.学校航模组有男生18人,女生15人;美术组有男生24人,女生20人。
(1)航模组男、女生人数的比和美术组男、女生人数的比能组成比例吗?
(2)如果能组成比例,指出比例的内项和外项。
【选自教材P41 练习七 第3题】
航模组 美术组
男生 18 24
女生 15 20
18∶15=24∶20
能组成比例。
外项
内项
8.小丽调制了两杯蜂蜜水,第一杯用了25毫升蜂蜜和200毫升水,第二杯用了30毫升蜂蜜和250毫升水。
(1)分别写出两杯蜂蜜水中蜂蜜与水体积的比,看看它们能否组成比例。
(2)按照第一杯蜂蜜水中蜂蜜与水体积的比计算,300毫升水中应加入蜂蜜多少毫升?
第一杯 第二杯
蜂蜜 25 30
水 200 250
不能
【选自教材P42 练习七 第8题】
第一杯 第三杯
蜂蜜 25 x
水 200 300
解:设300毫升水中应该加入x毫升蜂蜜。
25∶200=x∶300
200x=300×25
200x=7500
x=37.5
答:300毫升水中应该加入37.5毫升蜂蜜。
9.学校合唱组男生与女生的人数比是3∶4,合唱组男生有24人,女生有多少人?(你会用不同的方法解答吗?)
方法一:
24÷3=8(人)
4×8=32(人)
方法二:
设女生有x人。
3∶4=24∶x
3x=24×4
3x=96
x=32
答:女生有32人。
【选自教材P42 练习七 第9题】
如果 (m、n都不等于0),那么:
m∶n=( )∶( ), 。
解比例的一般步骤:
(1)根据比例的基本性质,把比例转化成两个外项的积和两个内项的积相等的形式;
(2)通过解方程求出未知项的值。
课堂小结
