六年级下册数学苏教版4.5 比例尺 课件 (共14张PPT)
文档属性
| 名称 | 六年级下册数学苏教版4.5 比例尺 课件 (共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-05 13:36:13 | ||
图片预览






文档简介
(共14张PPT)
比 例
比例尺
一个数与0.4、3.6和2一起可以组成比例,找出满足要求的数。
复习导入
0.4∶3.6=2∶a
0.4a=7.2
a=18
0.4∶2=a∶3.6
2a=0.4×3.6
a=0.72
0.4∶a=3.6∶2
3.6a=0.4×2
满足要求的数有18、0.72和 .
红光小学有一块长方形草坪,长50米,宽30米。把这块草坪按一定的比例缩小,画出的平面图长5厘米,宽3厘米。
你能分别写出草坪长、宽的图上距离和实际距离的比吗?
图上距离
实际
距离
图上距离 实际距离
长 5厘米 50米
宽 3厘米 30米
怎样写出5厘米和50米的比呢?
探究新知
图上距离 实际距离
长 5厘米 50米
宽 3厘米 30米
50米=5000厘米
图上的长和实际的长的比是:
5∶5000
=1∶1000
30米=3000厘米
图上的宽和实际的宽的比是:
3∶3000
=1∶1000
还有其他的写法吗?
图上距离 实际距离
长 5厘米 50米
宽 3厘米 30米
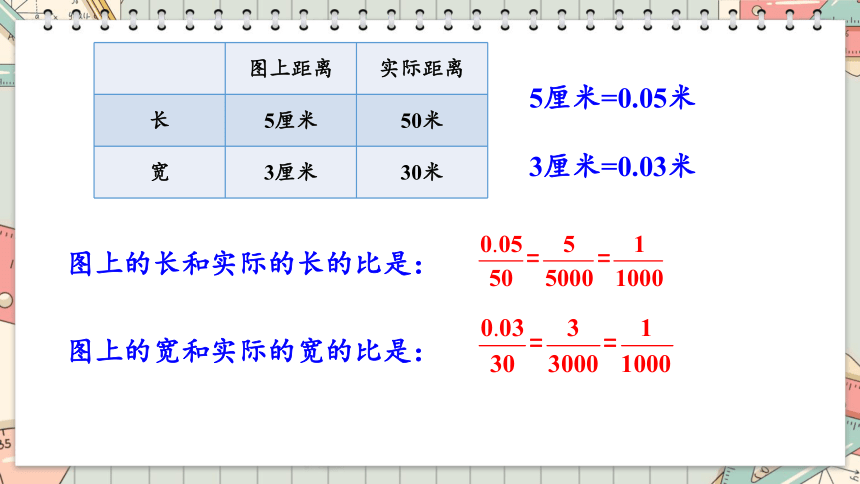
5厘米=0.05米
3厘米=0.03米
图上的长和实际的长的比是:
图上的宽和实际的宽的比是:
图上距离∶实际距离=比例尺
一幅图的图上距离和实际距离的比,叫作这幅图的比例尺。
或
多数情况下,绘制平面图或地图时都是实际距离按比例进行缩小的,为了便于比较,通常要把比例尺写成前项是1的比。
这幅平面图的比例尺是多少?
你能说说这个比例尺的含义吗?
1∶1000或
数值比例尺
1∶1000或
根据比例尺,可以知道图上距离1厘米表示实际距离10米。
比例尺1∶1000,表示实际距离是图上距离的1000倍。
比例尺1∶1000,表示图上距离是实际距离的 。
比例尺1∶1000还可以这样表示:
它表示图上1厘米的距离相当于实际距离10米。
线段比例尺能更直观地反映图上距离与实际距离的关系。
线段比例尺:
同一幅图中只用一个比例尺。
1.说出下面比例尺的实际意义。
图上1厘米表示实际距离22千米。
你能用其他形式表示图中的比例尺吗?
图上1厘米表示实际距离1500米。
【选自教材P44 练一练 第1题】
课堂练习
2.荷花村到杏树村的实际距离是15千米。量出这两个村的图上距离,并算出这幅图的比例尺。
15千米 = 1500000厘米
3∶1500000 = 1∶500000
答:这幅图的比例尺是1∶500000。
3cm
【选自教材P44 练一练 第2题】
3.判断题
(3)图上面积与实际面积的比是1∶160000( )
(1)图上长与实际长的比是400:1( )
把一块长20米,宽10米的长方形地画在图纸上,长画了5厘米,宽画了2.5厘米。
√
(2)图上宽与实际宽的比是1∶400( )
√
×
4.下面是实验小学体育场的平面图。体育场长150米,宽70米。求这幅图的比例尺,并在括号里填上合适的数。
7.5厘米
3.5厘米
150米=15000厘米
7.5∶15000=1∶2000
20
40
60
【选自教材P46 练习八 第2题】
图上距离∶实际距离=比例尺
一幅图的图上距离和实际距离的比,叫作这幅图的比例尺。
或
5∶5000
=1∶1000
课堂小结
比 例
比例尺
一个数与0.4、3.6和2一起可以组成比例,找出满足要求的数。
复习导入
0.4∶3.6=2∶a
0.4a=7.2
a=18
0.4∶2=a∶3.6
2a=0.4×3.6
a=0.72
0.4∶a=3.6∶2
3.6a=0.4×2
满足要求的数有18、0.72和 .
红光小学有一块长方形草坪,长50米,宽30米。把这块草坪按一定的比例缩小,画出的平面图长5厘米,宽3厘米。
你能分别写出草坪长、宽的图上距离和实际距离的比吗?
图上距离
实际
距离
图上距离 实际距离
长 5厘米 50米
宽 3厘米 30米
怎样写出5厘米和50米的比呢?
探究新知
图上距离 实际距离
长 5厘米 50米
宽 3厘米 30米
50米=5000厘米
图上的长和实际的长的比是:
5∶5000
=1∶1000
30米=3000厘米
图上的宽和实际的宽的比是:
3∶3000
=1∶1000
还有其他的写法吗?
图上距离 实际距离
长 5厘米 50米
宽 3厘米 30米
5厘米=0.05米
3厘米=0.03米
图上的长和实际的长的比是:
图上的宽和实际的宽的比是:
图上距离∶实际距离=比例尺
一幅图的图上距离和实际距离的比,叫作这幅图的比例尺。
或
多数情况下,绘制平面图或地图时都是实际距离按比例进行缩小的,为了便于比较,通常要把比例尺写成前项是1的比。
这幅平面图的比例尺是多少?
你能说说这个比例尺的含义吗?
1∶1000或
数值比例尺
1∶1000或
根据比例尺,可以知道图上距离1厘米表示实际距离10米。
比例尺1∶1000,表示实际距离是图上距离的1000倍。
比例尺1∶1000,表示图上距离是实际距离的 。
比例尺1∶1000还可以这样表示:
它表示图上1厘米的距离相当于实际距离10米。
线段比例尺能更直观地反映图上距离与实际距离的关系。
线段比例尺:
同一幅图中只用一个比例尺。
1.说出下面比例尺的实际意义。
图上1厘米表示实际距离22千米。
你能用其他形式表示图中的比例尺吗?
图上1厘米表示实际距离1500米。
【选自教材P44 练一练 第1题】
课堂练习
2.荷花村到杏树村的实际距离是15千米。量出这两个村的图上距离,并算出这幅图的比例尺。
15千米 = 1500000厘米
3∶1500000 = 1∶500000
答:这幅图的比例尺是1∶500000。
3cm
【选自教材P44 练一练 第2题】
3.判断题
(3)图上面积与实际面积的比是1∶160000( )
(1)图上长与实际长的比是400:1( )
把一块长20米,宽10米的长方形地画在图纸上,长画了5厘米,宽画了2.5厘米。
√
(2)图上宽与实际宽的比是1∶400( )
√
×
4.下面是实验小学体育场的平面图。体育场长150米,宽70米。求这幅图的比例尺,并在括号里填上合适的数。
7.5厘米
3.5厘米
150米=15000厘米
7.5∶15000=1∶2000
20
40
60
【选自教材P46 练习八 第2题】
图上距离∶实际距离=比例尺
一幅图的图上距离和实际距离的比,叫作这幅图的比例尺。
或
5∶5000
=1∶1000
课堂小结
