六年级下册数学苏教版6.2 认识正比例图像 课件 (共24张PPT)
文档属性
| 名称 | 六年级下册数学苏教版6.2 认识正比例图像 课件 (共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-05 13:39:35 | ||
图片预览

文档简介
(共24张PPT)
苏教版·六年级下册
认识正比例图像
复习导入
三角形的高一定,三角形的面积和底成正比例吗?为什么?
(一定)
即三角形的面积和底的比值一定,它们成正比例。
探索新知
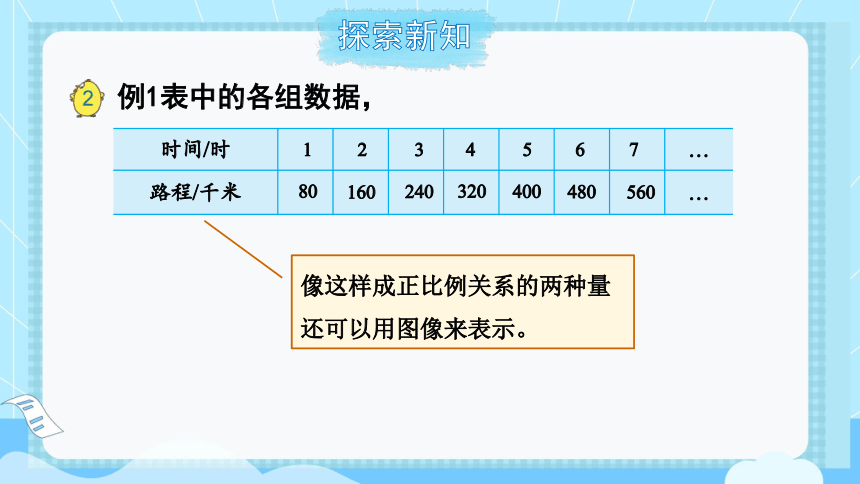
像这样成正比例关系的两种量还可以用图像来表示。
时间/时 …
路程/千米 …
1
80
2
160
240
320
400
480
560
3
4
5
6
7
例1表中的各组数据,
探索新知
时间/时 …
路程/千米 …
1
80
2
160
240
320
400
480
560
3
4
5
6
7
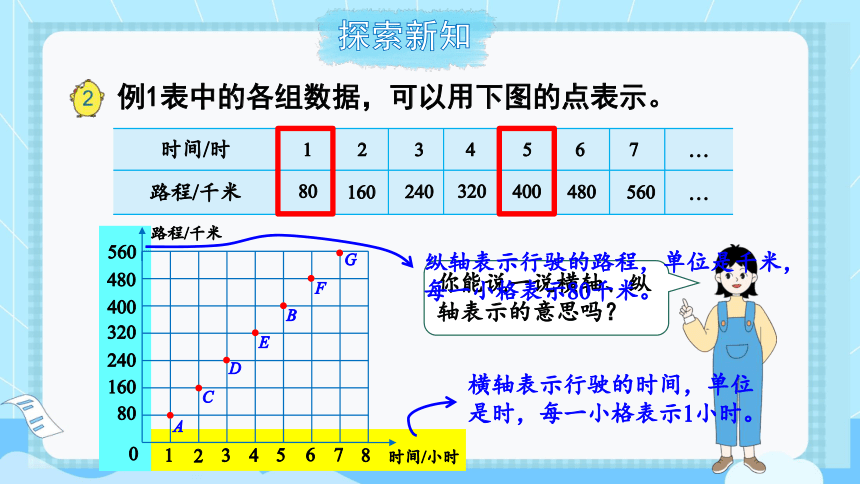
例1表中的各组数据,可以用下图的点表示。
你能说一说横轴、纵轴表示的意思吗?
时间/小时
1
2
3
4
5
6
7
8
0
路程/千米
80
160
240
320
400
480
560
A
C
D
E
B
F
G
横轴表示行驶的时间,单位是时,每一小格表示1小时。
纵轴表示行驶的路程,单位是千米,每一小格表示80千米。
【提示:点击C、D、E、F、G点显示】
探索新知
时间/时 …
路程/千米 …
1
80
2
160
240
320
400
480
560
3
4
5
6
7
时间/小时
1
2
3
4
5
6
7
8
0
路程/千米
80
160
240
320
400
480
560
A
C
D
E
B
F
G
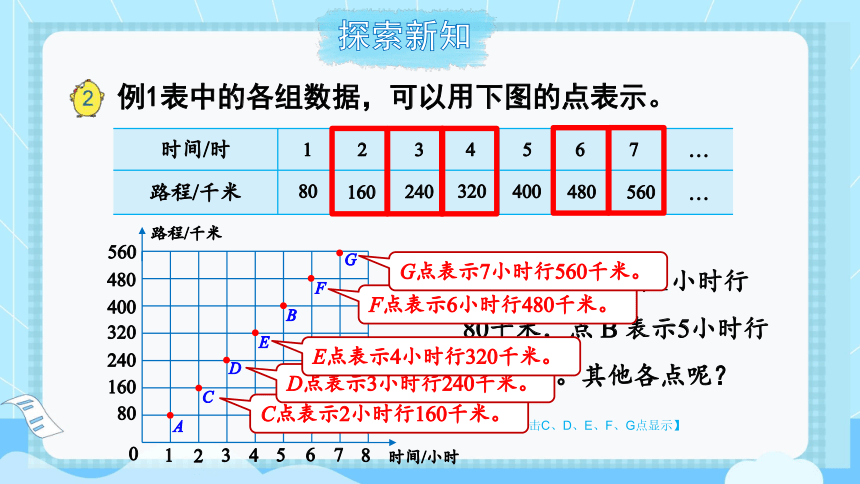
(1)图中的点 A 表示1小时行 80千米,点 B 表示5小时行400千米。其他各点呢?
C点表示2小时行160千米。
D点表示3小时行240千米。
E点表示4小时行320千米。
F点表示6小时行480千米。
G点表示7小时行560千米。
例1表中的各组数据,可以用下图的点表示。
探索新知
时间/时 …
路程/千米 …
1
80
2
160
240
320
400
480
560
3
4
5
6
7
时间/小时
1
2
3
4
5
6
7
8
0
路程/千米
80
160
240
320
400
480
560
A
C
D
E
B
F
G
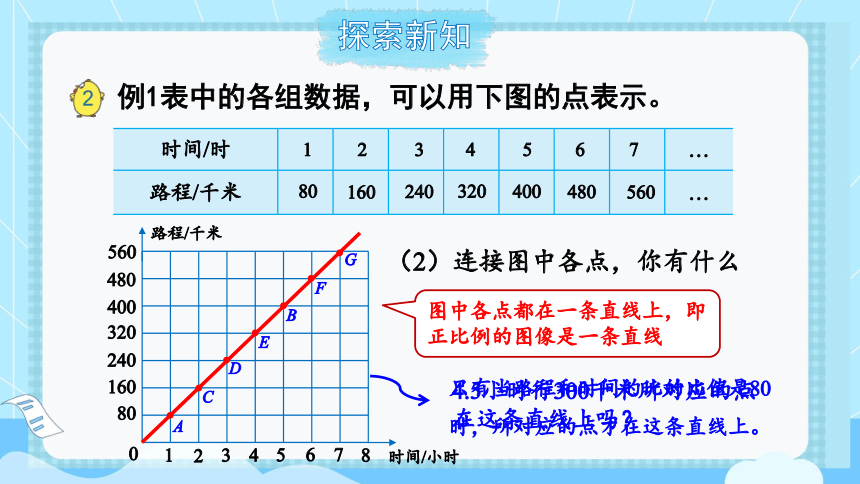
(2)连接图中各点,你有什么发现?
图中各点都在一条直线上,即正比例的图像是一条直线
4.5小时行300千米所对应的点在这条直线上吗?
只有当路程和时间的比的比值是80时,所对应的点才在这条直线上。
例1表中的各组数据,可以用下图的点表示。
探索新知
时间/时 …
路程/千米 …
1
80
2
160
240
320
400
480
560
3
4
5
6
7
时间/小时
1
2
3
4
5
6
7
8
0
路程/千米
80
160
240
320
400
480
560
A
C
D
E
B
F
G
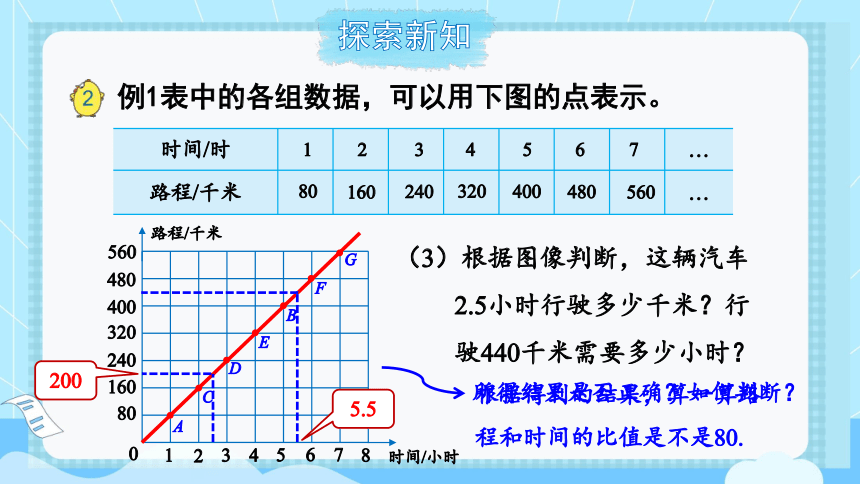
(3)根据图像判断,这辆汽车2.5小时行驶多少千米?行驶440千米需要多少小时?
200
5.5
所得结果是否正确?如何判断?
根据得到的结果,算一算路程和时间的比值是不是80.
例1表中的各组数据,可以用下图的点表示。
小玲用计算机打字的数量和所用的时间如下表:
时间/分 …
数量/个 …
2
100
4
200
300
400
500
600
700
6
8
10
12
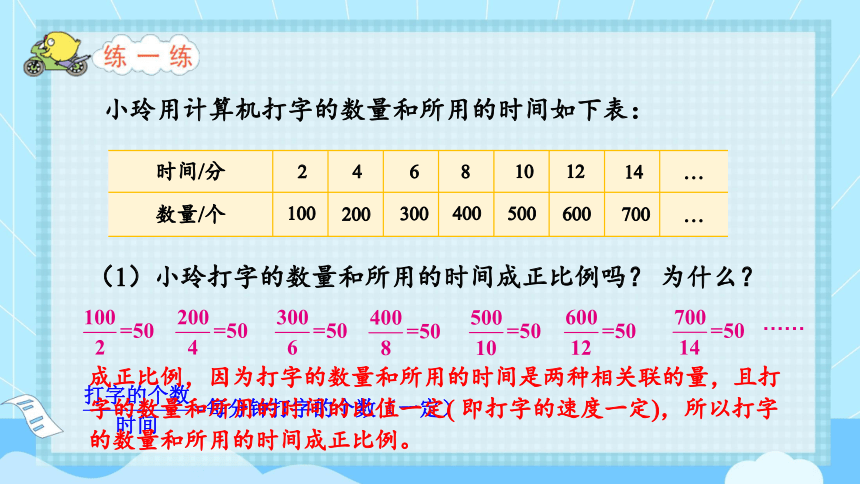
(1)小玲打字的数量和所用的时间成正比例吗? 为什么?
……
成正比例,因为打字的数量和所用的时间是两种相关联的量,且打字的数量和所用的时间的比值一定( 即打字的速度一定),所以打字的数量和所用的时间成正比例。
14
小玲用计算机打字的数量和所用的时间如下表:
时间/分 …
数量/个 …
2
100
4
200
300
400
500
600
700
6
8
10
12
14
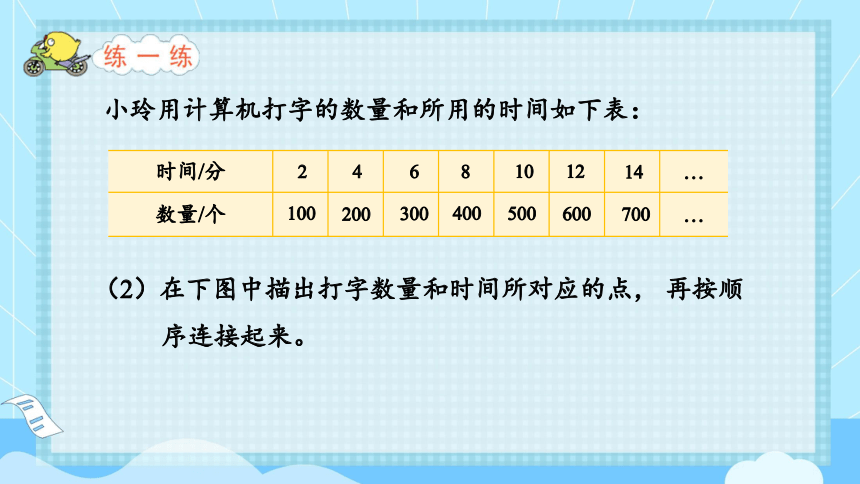
(2)在下图中描出打字数量和时间所对应的点, 再按顺序连接起来。
时间/分 …
数量/个 …
2
100
4
200
300
400
500
600
700
6
8
10
12
14
先描点,后连线。
画出的图象要越过表示14分钟打700个字所对应的点
(3)根据图像判断,小玲5分钟可以打多少个字?打750个字需要多少分钟?
5分钟可
以打250个字
打750个字需要15分钟
观察这两个成正比例关系的图像,你发现了什么?
归
纳
正比例关系的图像是一条经过原点的射线。
从图像中可以直观地看出两种量的变化情况。
借助图像,可以由一个量的值找到对应的另一个量的值。
随堂练习
【选自教材P60 练习十 第4题】
1. 一种彩带每米售价5元,购买2米、3米······各需要多少元?
长度/米
总价/元
1
5
2
(1)把下表填写完整。
10
3
4
5
15
20
25
(2)根据表中的数据,在下图中描出彩带总价和长度所对应的点,再按顺序连接起来。
长度/米
总价/元
1
5
2
10
3
4
5
15
20
25
长度/米
1
2
3
4
5
6
7
8
0
总价/元
5
10
15
20
25
(3)购买彩带的总价和长度成正比例吗?你是根据什么来判断的?
长度/米
1
2
3
4
5
6
7
8
0
总价/元
5
10
15
20
25
长度/米
总价/元
1
5
2
10
3
4
5
15
20
25
利用表格中的数据,发现:
所以彩带的总价和长度成正比例。
通过绘制的图像,发现:这是一条经过原点的直线。
所以彩带的总价和长度成正比例。
长度/米
1
2
3
4
5
6
7
8
0
总价/元
5
10
15
20
25
(4)根据图像判断,购买3.5米彩带需要多少元?
购买3.5米彩带需要17.5元。
2. 一根弹簧挂上物体(质量不超过20千克)后长度会伸长,物体的质量与伸长的长度如下:
物体质量/kg …
弹簧伸长长度/cm …
2
0.5
4
1
1.5
2
2.5
5
6
8
10
20
这是什么意思?
超过20千克,弹簧会变形,无法恢复原状。
2. 一根弹簧挂上物体(质量不超过20千克)后长度会伸长,物体的质量与伸长的长度如下:
(1)在图中描出物体的质量和弹簧伸长的长度所对应的点,再按顺序连接起来。
物体质量/kg …
弹簧伸长长度/cm …
2
0.5
4
1
1.5
2
2.5
5
6
8
10
20
物体质量/kg …
弹簧伸长长度/cm …
2
0.5
4
1
1.5
2
2.5
5
6
8
10
20
(2)物体的质量与弹簧伸长的长度成正比例吗?为什么?
物体质量/kg …
弹簧伸长长度/cm …
2
0.5
4
1
1.5
2
2.5
5
6
8
10
20
弹簧伸长的长度与所挂物体的质量是两种相关联的量且比值一定。
成正比例!
(3)根据图像判断,如果挂上质量是5千克的物体,弹簧应伸长多少厘米?要使弹簧伸长4厘米,应挂上多少千克的物体?
挂上质量是5千克的物体,弹簧应伸长1.25厘米。
要使弹簧伸长4厘米,应挂上16千克的物体。
(3)根据图像判断,如果挂上质量是5千克的物体,弹簧应伸长多少厘米?要使弹簧伸长4厘米,应挂上多少千克的物体?
课堂小结
正比例关系的图像是一条经过原点的直线。
从图像中可以直观地看出两种量的变化情况。
借助图像,可以由一个量的值找到对应的另一个量的值。
苏教版·六年级下册
认识正比例图像
复习导入
三角形的高一定,三角形的面积和底成正比例吗?为什么?
(一定)
即三角形的面积和底的比值一定,它们成正比例。
探索新知
像这样成正比例关系的两种量还可以用图像来表示。
时间/时 …
路程/千米 …
1
80
2
160
240
320
400
480
560
3
4
5
6
7
例1表中的各组数据,
探索新知
时间/时 …
路程/千米 …
1
80
2
160
240
320
400
480
560
3
4
5
6
7
例1表中的各组数据,可以用下图的点表示。
你能说一说横轴、纵轴表示的意思吗?
时间/小时
1
2
3
4
5
6
7
8
0
路程/千米
80
160
240
320
400
480
560
A
C
D
E
B
F
G
横轴表示行驶的时间,单位是时,每一小格表示1小时。
纵轴表示行驶的路程,单位是千米,每一小格表示80千米。
【提示:点击C、D、E、F、G点显示】
探索新知
时间/时 …
路程/千米 …
1
80
2
160
240
320
400
480
560
3
4
5
6
7
时间/小时
1
2
3
4
5
6
7
8
0
路程/千米
80
160
240
320
400
480
560
A
C
D
E
B
F
G
(1)图中的点 A 表示1小时行 80千米,点 B 表示5小时行400千米。其他各点呢?
C点表示2小时行160千米。
D点表示3小时行240千米。
E点表示4小时行320千米。
F点表示6小时行480千米。
G点表示7小时行560千米。
例1表中的各组数据,可以用下图的点表示。
探索新知
时间/时 …
路程/千米 …
1
80
2
160
240
320
400
480
560
3
4
5
6
7
时间/小时
1
2
3
4
5
6
7
8
0
路程/千米
80
160
240
320
400
480
560
A
C
D
E
B
F
G
(2)连接图中各点,你有什么发现?
图中各点都在一条直线上,即正比例的图像是一条直线
4.5小时行300千米所对应的点在这条直线上吗?
只有当路程和时间的比的比值是80时,所对应的点才在这条直线上。
例1表中的各组数据,可以用下图的点表示。
探索新知
时间/时 …
路程/千米 …
1
80
2
160
240
320
400
480
560
3
4
5
6
7
时间/小时
1
2
3
4
5
6
7
8
0
路程/千米
80
160
240
320
400
480
560
A
C
D
E
B
F
G
(3)根据图像判断,这辆汽车2.5小时行驶多少千米?行驶440千米需要多少小时?
200
5.5
所得结果是否正确?如何判断?
根据得到的结果,算一算路程和时间的比值是不是80.
例1表中的各组数据,可以用下图的点表示。
小玲用计算机打字的数量和所用的时间如下表:
时间/分 …
数量/个 …
2
100
4
200
300
400
500
600
700
6
8
10
12
(1)小玲打字的数量和所用的时间成正比例吗? 为什么?
……
成正比例,因为打字的数量和所用的时间是两种相关联的量,且打字的数量和所用的时间的比值一定( 即打字的速度一定),所以打字的数量和所用的时间成正比例。
14
小玲用计算机打字的数量和所用的时间如下表:
时间/分 …
数量/个 …
2
100
4
200
300
400
500
600
700
6
8
10
12
14
(2)在下图中描出打字数量和时间所对应的点, 再按顺序连接起来。
时间/分 …
数量/个 …
2
100
4
200
300
400
500
600
700
6
8
10
12
14
先描点,后连线。
画出的图象要越过表示14分钟打700个字所对应的点
(3)根据图像判断,小玲5分钟可以打多少个字?打750个字需要多少分钟?
5分钟可
以打250个字
打750个字需要15分钟
观察这两个成正比例关系的图像,你发现了什么?
归
纳
正比例关系的图像是一条经过原点的射线。
从图像中可以直观地看出两种量的变化情况。
借助图像,可以由一个量的值找到对应的另一个量的值。
随堂练习
【选自教材P60 练习十 第4题】
1. 一种彩带每米售价5元,购买2米、3米······各需要多少元?
长度/米
总价/元
1
5
2
(1)把下表填写完整。
10
3
4
5
15
20
25
(2)根据表中的数据,在下图中描出彩带总价和长度所对应的点,再按顺序连接起来。
长度/米
总价/元
1
5
2
10
3
4
5
15
20
25
长度/米
1
2
3
4
5
6
7
8
0
总价/元
5
10
15
20
25
(3)购买彩带的总价和长度成正比例吗?你是根据什么来判断的?
长度/米
1
2
3
4
5
6
7
8
0
总价/元
5
10
15
20
25
长度/米
总价/元
1
5
2
10
3
4
5
15
20
25
利用表格中的数据,发现:
所以彩带的总价和长度成正比例。
通过绘制的图像,发现:这是一条经过原点的直线。
所以彩带的总价和长度成正比例。
长度/米
1
2
3
4
5
6
7
8
0
总价/元
5
10
15
20
25
(4)根据图像判断,购买3.5米彩带需要多少元?
购买3.5米彩带需要17.5元。
2. 一根弹簧挂上物体(质量不超过20千克)后长度会伸长,物体的质量与伸长的长度如下:
物体质量/kg …
弹簧伸长长度/cm …
2
0.5
4
1
1.5
2
2.5
5
6
8
10
20
这是什么意思?
超过20千克,弹簧会变形,无法恢复原状。
2. 一根弹簧挂上物体(质量不超过20千克)后长度会伸长,物体的质量与伸长的长度如下:
(1)在图中描出物体的质量和弹簧伸长的长度所对应的点,再按顺序连接起来。
物体质量/kg …
弹簧伸长长度/cm …
2
0.5
4
1
1.5
2
2.5
5
6
8
10
20
物体质量/kg …
弹簧伸长长度/cm …
2
0.5
4
1
1.5
2
2.5
5
6
8
10
20
(2)物体的质量与弹簧伸长的长度成正比例吗?为什么?
物体质量/kg …
弹簧伸长长度/cm …
2
0.5
4
1
1.5
2
2.5
5
6
8
10
20
弹簧伸长的长度与所挂物体的质量是两种相关联的量且比值一定。
成正比例!
(3)根据图像判断,如果挂上质量是5千克的物体,弹簧应伸长多少厘米?要使弹簧伸长4厘米,应挂上多少千克的物体?
挂上质量是5千克的物体,弹簧应伸长1.25厘米。
要使弹簧伸长4厘米,应挂上16千克的物体。
(3)根据图像判断,如果挂上质量是5千克的物体,弹簧应伸长多少厘米?要使弹簧伸长4厘米,应挂上多少千克的物体?
课堂小结
正比例关系的图像是一条经过原点的直线。
从图像中可以直观地看出两种量的变化情况。
借助图像,可以由一个量的值找到对应的另一个量的值。
