4.3.2 角的比较与运算(1) 课件 (共25张PPT)
文档属性
| 名称 | 4.3.2 角的比较与运算(1) 课件 (共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-06 19:38:58 | ||
图片预览



文档简介
(共25张PPT)
人教版 七年级上册
4.3.2角的比较与运算(1)
课件说明
1.知道比较角的大小的两种方法;
教学目标
2.掌握角平分线的定义.
教学重点:
角平分线的定义及表示方法.
填空:
(1)48°35′+17°45′= ;
(3)15°20′×5= ;
66°20′
76°40′
(2)48°18′-17°45′= ;
=30°33′
(4)360°÷24= .
15°
1°的60分之一为1分,记作“1′”,即1°=60′
1′的60分之一为1秒,记作“1″”,即1′=60″.
复习旧知
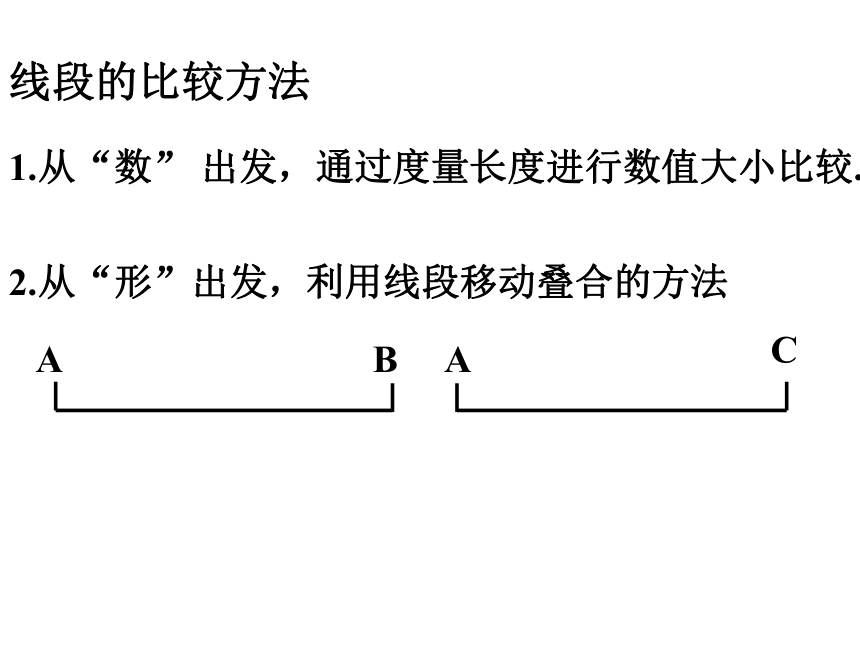
线段的比较方法
2.从“形”出发,利用线段移动叠合的方法
A
B
A
C
1.从“数” 出发,通过度量长度进行数值大小比较.
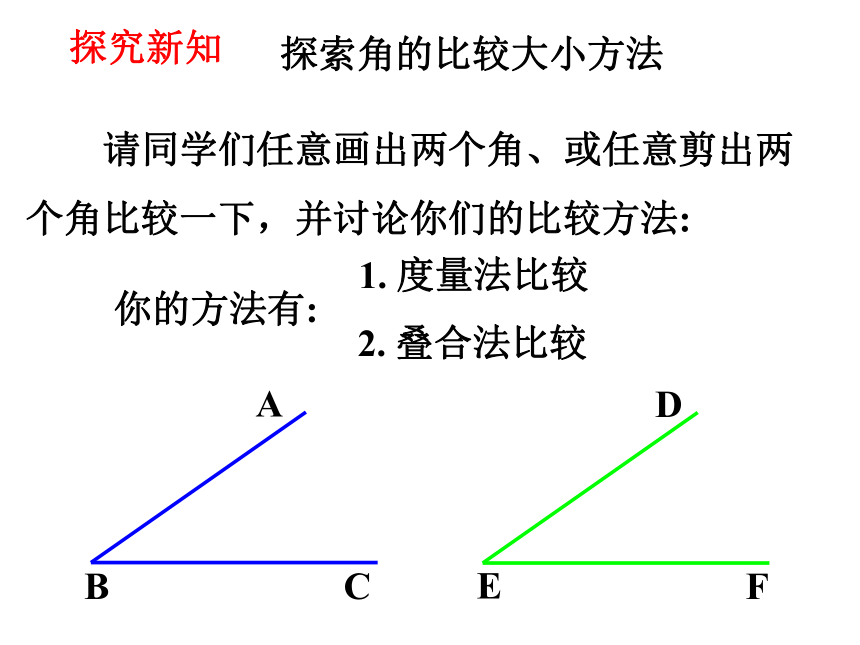
探索角的比较大小方法
请同学们任意画出两个角、或任意剪出两个角比较一下,并讨论你们的比较方法:
B
A
C
E
D
F
你的方法有:
1. 度量法比较
2. 叠合法比较
探究新知
45°
60°
A
O
B
D
E
F
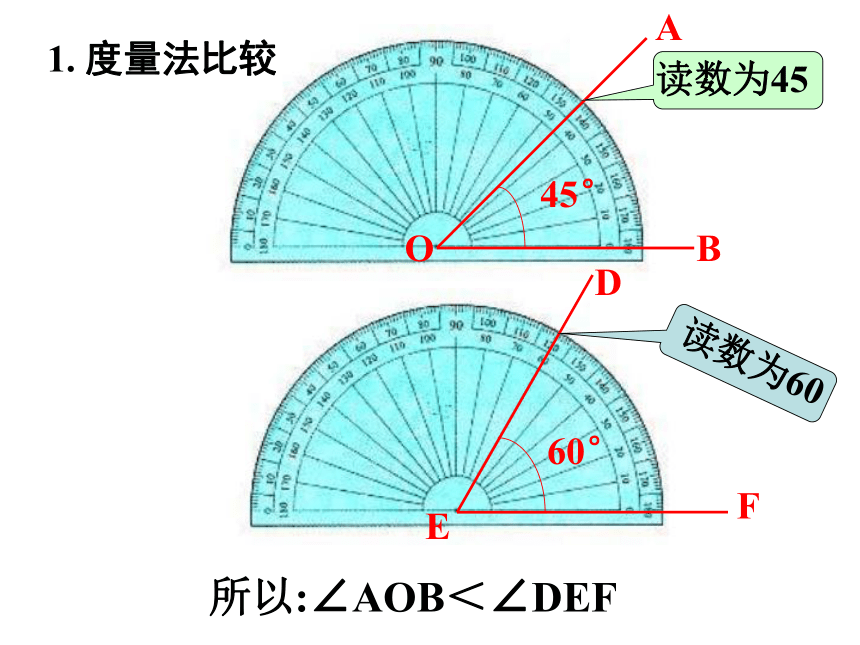
所以:∠AOB<∠DEF
读数为45
读数为60
1. 度量法比较
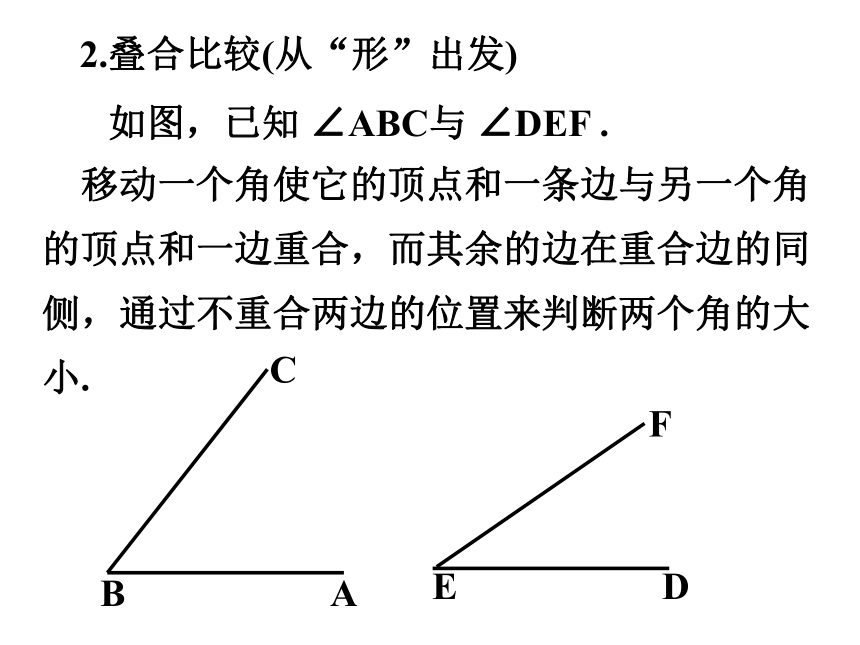
2.叠合比较(从“形”出发)
如图,已知 ∠ABC与 ∠DEF .
D
E
F
A
B
C
移动一个角使它的顶点和一条边与另一个角的顶点和一边重合,而其余的边在重合边的同侧,通过不重合两边的位置来判断两个角的大小.
A
B
C
F
(E)
(D)
A
B
C
(E)
(D)
(F)
A
B
C
F
(E)
(D)
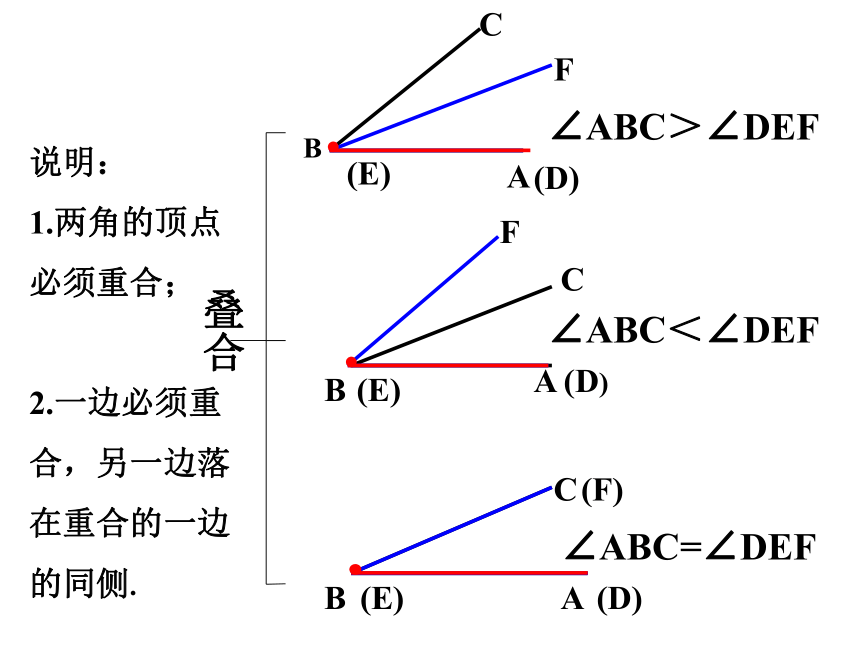
叠合
∠ABC>∠DEF
说明:
1.两角的顶点必须重合;
2.一边必须重合,另一边落在重合的一边的同侧.
∠ABC<∠DEF
∠ABC=∠DEF
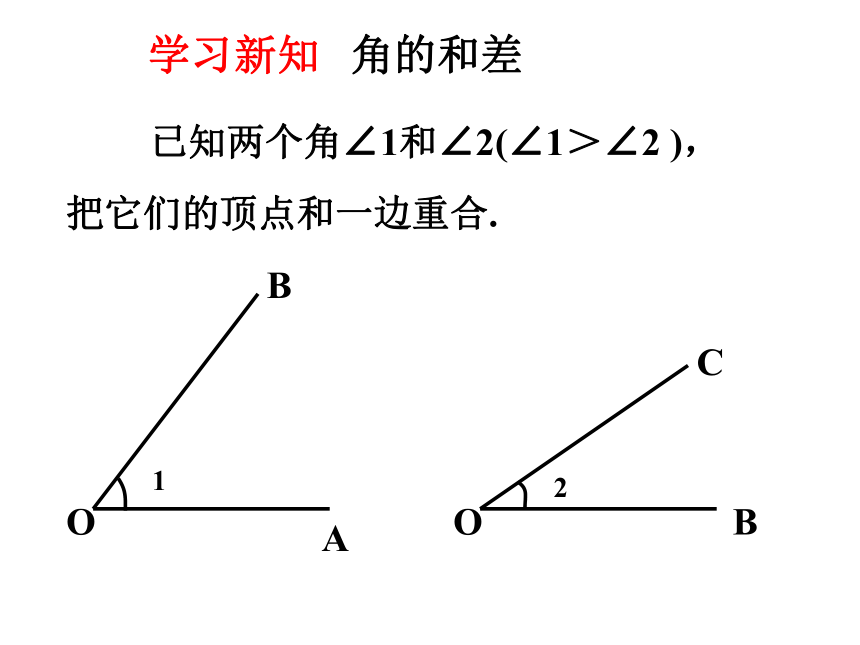
已知两个角∠1和∠2(∠1>∠2 ),
把它们的顶点和一边重合.
1
2
A
O
B
B
O
C
角的和差
学习新知
1
O
A
B
2
C
B
O
A
1
B
O
O
B
C
2
∠AOC为∠1 与∠2 的和
记作 ∠AOC =∠1+∠2
顶点与一边重合
∠AOC为∠1 与∠2 的差
记作 ∠AOC =∠1-∠2
1.请你试用一对三角尺根据刚才学过的角的和差
知识拼出所有的特殊角.
180°
75°
150°
135°
120°
105°
15°
165°
练习巩固
O
A
C
B
2.下图中共有几个角?它们有什么关系?
完成下列问题:
1.图中共有__个角,
它们分别是____________
2.∠AOB=____+_____
3.∠AOC=____-_____
4.∠BOC=____-_____.
3
∠AOB、
∠AOC ∠BOC
∠AOB ∠BOC
∠AOB ∠AOC
∠BOC.
∠AOC 、
3.按图1填空:
4)∠AOB +∠BOC=
5)∠AOC+∠COD=
6)∠BOD-∠COD=
7)∠AOD-
=∠AOB
O
D
C
B
A
图1
∠AOC
∠AOD
∠BOC
∠BOD
1)∠DOB ∠BOC
2)∠COB ∠AOC
3)∠DOC +∠COB ∠BOD
>
<
=
A
B
D
C
(1) ∠DAB = ∠DAC+
(2) ∠ACB =∠DCB -
∠CAB
∠DCA
(3)∠ABC = ∠ABD ∠CBD
(4)∠BDC = ∠ADC ∠BDA
+
-
A
B
D
C
4.看图填空:
B
O
C
A
从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的角平分线.
在一张纸上画出一个角 ∠AOC 并剪下,将这个角对折,使其两边重合,折痕记作OB,它与角两边所成的两个角的大小有什么关系?
学习新知
-
2
1
(或∠AOC=2∠AOB =2∠COB)
∵OB是∠AOB的平分线,
∴∠AOB=∠COB =
∠AOC
从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的角平分线.
O
C
A
B
∠AOB=∠BOC= ∠COD,
则OB 是 的平分线,
∠BOC = ∠AOC,
∠BOC= ∠BOD,
∠BOC = ∠ AOD, ∠BOD = ∠AOD.
A
B
C
D
O
∠AOC
此时OB、OC叫∠ AOD的三等份线.
-
2
1
-
2
1
-
3
1
-
3
2
A
B
C
D
E
∵AD是∠BAC的平分线,
∴∠DAC=∠BAD=
∴∠BAC=2∠BAD=
∵BE是∠ABC的平分线,
∴∠EBC=∠ABE=
∠ABC
41°36′12″.
2×41°36′12″
=82°72′24″
=83°12′24″.
= ×75°12′
1
2
1
2
=37°36′.
解:
如图 , 已知,AD、BE分别是∠BAC和∠ABC
的平分线,且∠BAD=41°35′12″, ∠ABC=75°12′.
求∠ DAC、 ∠ BAC、 ∠ EBC 、∠ ABE的度数.
例题解析
A
B
C
D
O
如图 , 已知,OB、OC是∠AOD的三等分线,∠AOB=30°34′22″,求∠AOC、 ∠ AOD的度数.
∵OB、OC是∠AOD的三等分线,
解:
∴ ∠AOC= 2∠AOB
= 2× 30°34′22″
= 60°68′44″
= 61°8′44″
∠AOD= 3∠AOB
= 3× 30°34′22″
= 90°102′66″
= 91°43′6″
答:∠AOC= 61°8′44″, ∠ AOD= 91°43′6″.
练习巩固
(1)比较角的大小有哪两种方法?
①度量法; ②叠合法.
(2)由角平分线的定义,可以得到哪些相等的关系式?
课堂小结
1.如图 , 射线OB、OC将∠AOD分为三部分,
如果∠AOC>∠BOD,那么∠AOB与∠COD
的大小关系是( ).
A. ∠AOB>∠COD B. ∠AOB与∠COD
C. ∠AOB=∠COD D. 无法判断
D
C
B
A
O
练习巩固
2.已知∠AOB=30°,∠BOC=80°,∠AOC=50°,
则下列说法正确的是( ).
A. 射线OB在∠AOC内, B. 射线OB在∠AOC外
C. 射线OB与射线OA重合 D. 射线OB与射线OC重合
A
B
3.如图 , 已知OC平分∠BOD,∠AOD=110°,
∠COD=35°,则∠AOB= °,∠ AOC= °.
4.如图 , 已知∠COB=2∠AOC,OD平分∠AOB,
∠COD=20°,则∠AOB= °.
A
B
C
D
O
A
B
C
D
O
40
75
120
今天作业
课本P134习题第1、2题
课本P139习题第3题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 七年级上册
4.3.2角的比较与运算(1)
课件说明
1.知道比较角的大小的两种方法;
教学目标
2.掌握角平分线的定义.
教学重点:
角平分线的定义及表示方法.
填空:
(1)48°35′+17°45′= ;
(3)15°20′×5= ;
66°20′
76°40′
(2)48°18′-17°45′= ;
=30°33′
(4)360°÷24= .
15°
1°的60分之一为1分,记作“1′”,即1°=60′
1′的60分之一为1秒,记作“1″”,即1′=60″.
复习旧知
线段的比较方法
2.从“形”出发,利用线段移动叠合的方法
A
B
A
C
1.从“数” 出发,通过度量长度进行数值大小比较.
探索角的比较大小方法
请同学们任意画出两个角、或任意剪出两个角比较一下,并讨论你们的比较方法:
B
A
C
E
D
F
你的方法有:
1. 度量法比较
2. 叠合法比较
探究新知
45°
60°
A
O
B
D
E
F
所以:∠AOB<∠DEF
读数为45
读数为60
1. 度量法比较
2.叠合比较(从“形”出发)
如图,已知 ∠ABC与 ∠DEF .
D
E
F
A
B
C
移动一个角使它的顶点和一条边与另一个角的顶点和一边重合,而其余的边在重合边的同侧,通过不重合两边的位置来判断两个角的大小.
A
B
C
F
(E)
(D)
A
B
C
(E)
(D)
(F)
A
B
C
F
(E)
(D)
叠合
∠ABC>∠DEF
说明:
1.两角的顶点必须重合;
2.一边必须重合,另一边落在重合的一边的同侧.
∠ABC<∠DEF
∠ABC=∠DEF
已知两个角∠1和∠2(∠1>∠2 ),
把它们的顶点和一边重合.
1
2
A
O
B
B
O
C
角的和差
学习新知
1
O
A
B
2
C
B
O
A
1
B
O
O
B
C
2
∠AOC为∠1 与∠2 的和
记作 ∠AOC =∠1+∠2
顶点与一边重合
∠AOC为∠1 与∠2 的差
记作 ∠AOC =∠1-∠2
1.请你试用一对三角尺根据刚才学过的角的和差
知识拼出所有的特殊角.
180°
75°
150°
135°
120°
105°
15°
165°
练习巩固
O
A
C
B
2.下图中共有几个角?它们有什么关系?
完成下列问题:
1.图中共有__个角,
它们分别是____________
2.∠AOB=____+_____
3.∠AOC=____-_____
4.∠BOC=____-_____.
3
∠AOB、
∠AOC ∠BOC
∠AOB ∠BOC
∠AOB ∠AOC
∠BOC.
∠AOC 、
3.按图1填空:
4)∠AOB +∠BOC=
5)∠AOC+∠COD=
6)∠BOD-∠COD=
7)∠AOD-
=∠AOB
O
D
C
B
A
图1
∠AOC
∠AOD
∠BOC
∠BOD
1)∠DOB ∠BOC
2)∠COB ∠AOC
3)∠DOC +∠COB ∠BOD
>
<
=
A
B
D
C
(1) ∠DAB = ∠DAC+
(2) ∠ACB =∠DCB -
∠CAB
∠DCA
(3)∠ABC = ∠ABD ∠CBD
(4)∠BDC = ∠ADC ∠BDA
+
-
A
B
D
C
4.看图填空:
B
O
C
A
从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的角平分线.
在一张纸上画出一个角 ∠AOC 并剪下,将这个角对折,使其两边重合,折痕记作OB,它与角两边所成的两个角的大小有什么关系?
学习新知
-
2
1
(或∠AOC=2∠AOB =2∠COB)
∵OB是∠AOB的平分线,
∴∠AOB=∠COB =
∠AOC
从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的角平分线.
O
C
A
B
∠AOB=∠BOC= ∠COD,
则OB 是 的平分线,
∠BOC = ∠AOC,
∠BOC= ∠BOD,
∠BOC = ∠ AOD, ∠BOD = ∠AOD.
A
B
C
D
O
∠AOC
此时OB、OC叫∠ AOD的三等份线.
-
2
1
-
2
1
-
3
1
-
3
2
A
B
C
D
E
∵AD是∠BAC的平分线,
∴∠DAC=∠BAD=
∴∠BAC=2∠BAD=
∵BE是∠ABC的平分线,
∴∠EBC=∠ABE=
∠ABC
41°36′12″.
2×41°36′12″
=82°72′24″
=83°12′24″.
= ×75°12′
1
2
1
2
=37°36′.
解:
如图 , 已知,AD、BE分别是∠BAC和∠ABC
的平分线,且∠BAD=41°35′12″, ∠ABC=75°12′.
求∠ DAC、 ∠ BAC、 ∠ EBC 、∠ ABE的度数.
例题解析
A
B
C
D
O
如图 , 已知,OB、OC是∠AOD的三等分线,∠AOB=30°34′22″,求∠AOC、 ∠ AOD的度数.
∵OB、OC是∠AOD的三等分线,
解:
∴ ∠AOC= 2∠AOB
= 2× 30°34′22″
= 60°68′44″
= 61°8′44″
∠AOD= 3∠AOB
= 3× 30°34′22″
= 90°102′66″
= 91°43′6″
答:∠AOC= 61°8′44″, ∠ AOD= 91°43′6″.
练习巩固
(1)比较角的大小有哪两种方法?
①度量法; ②叠合法.
(2)由角平分线的定义,可以得到哪些相等的关系式?
课堂小结
1.如图 , 射线OB、OC将∠AOD分为三部分,
如果∠AOC>∠BOD,那么∠AOB与∠COD
的大小关系是( ).
A. ∠AOB>∠COD B. ∠AOB与∠COD
C. ∠AOB=∠COD D. 无法判断
D
C
B
A
O
练习巩固
2.已知∠AOB=30°,∠BOC=80°,∠AOC=50°,
则下列说法正确的是( ).
A. 射线OB在∠AOC内, B. 射线OB在∠AOC外
C. 射线OB与射线OA重合 D. 射线OB与射线OC重合
A
B
3.如图 , 已知OC平分∠BOD,∠AOD=110°,
∠COD=35°,则∠AOB= °,∠ AOC= °.
4.如图 , 已知∠COB=2∠AOC,OD平分∠AOB,
∠COD=20°,则∠AOB= °.
A
B
C
D
O
A
B
C
D
O
40
75
120
今天作业
课本P134习题第1、2题
课本P139习题第3题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
