3.3.1抛物线及其标准方程 课件-2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册(共20张PPT)
文档属性
| 名称 | 3.3.1抛物线及其标准方程 课件-2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-06 09:53:43 | ||
图片预览






文档简介
(共20张PPT)
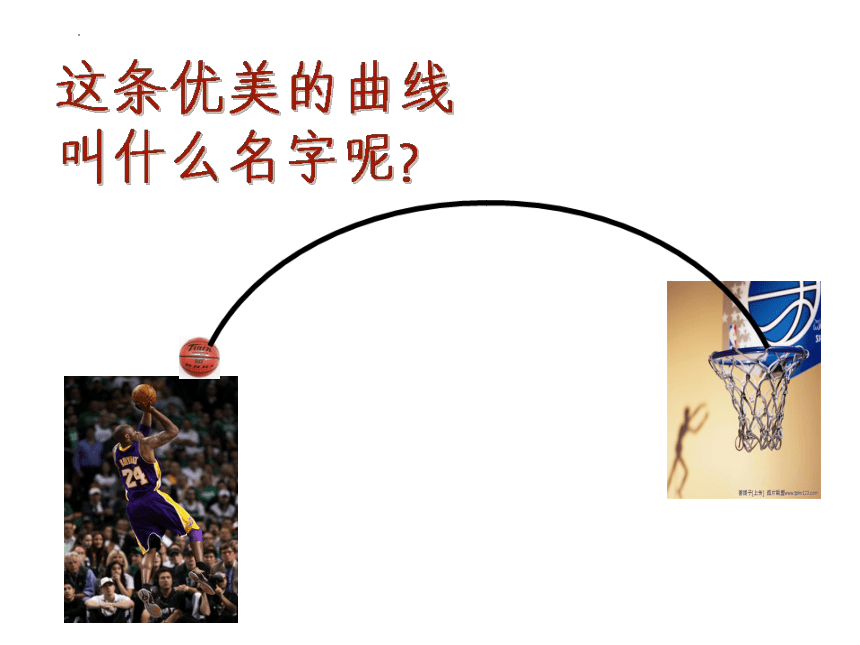
生活中存在着各种形式的抛物线
数学这门学科不仅需要观察,还需要实验。
——欧拉抛物线的形成.gsp
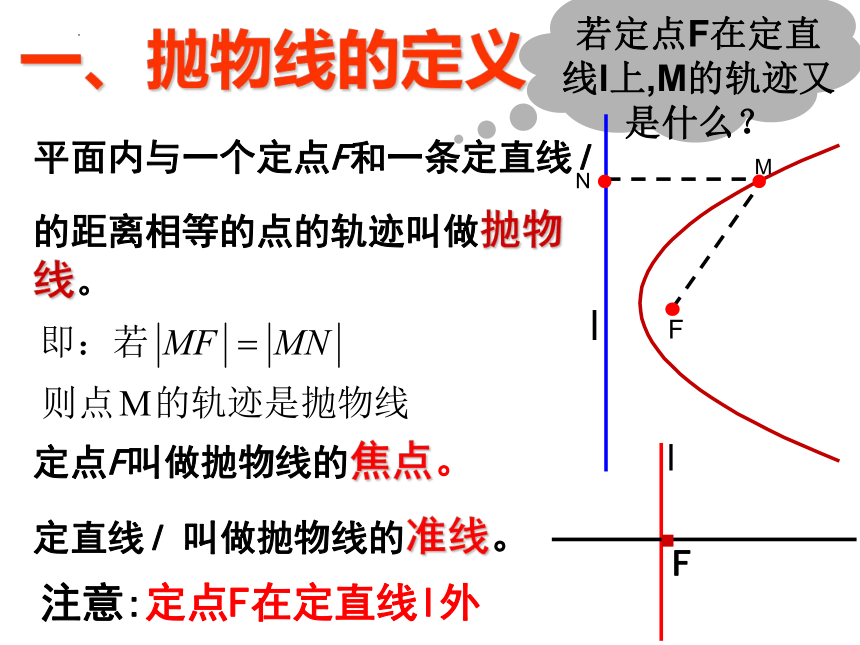
平面内与一个定点F和一条定直线l
的距离相等的点的轨迹叫做抛物线。
一、抛物线的定义
定点F叫做抛物线的焦点。
定直线l 叫做抛物线的准线。
若定点F在定直线l上,M的轨迹又是什么?
F
l
·
l
F
M
N
注意:定点F在定直线l外
仿照求椭圆、双曲线标准方程的方法,如何求抛物线的标准方程?
如何建系呢?
l
解:以过F且垂直于 l 的直线为x轴,垂足为K.以F,K的中点O为坐标原点建立直角坐标系xoy.
两边平方,整理得
x
K
y
o
M(x,y)
F
二、标准方程的推导
把方程 y2 = 2px (p>0)叫做抛物线的标准方程.其中 p 为正常数.
且p 的几何意义是:
焦点坐标是:
准线方程为:
焦点到准线的距离
想一想: 在建立椭圆、双曲线的标准方程时,选择不同的坐标系得到了不同形式的标准方程,那么,抛物线的标准方程有哪些不同的形式?
﹒
y
x
o
(1)
﹒
y
x
o
(2)
﹒
y
x
o
(3)
﹒
y
x
o
(4)
y2=-2px
(p>0)
x2=2py
(p>0)
准线方程
焦点坐标
标准方程
图 形
x
F
O
y
l
x
F
O
y
l
x
F
O
y
l
x
F
O
y
l
y2=2px
(p>0)
x2=-2py
(p>0)
P的意义:抛物线的焦点到准线的距离
方程的特点:
(1)左边是二次项,且系数为1
(2)右边是一次式;决定了焦点的位置和开口方向(看一次项系数的正负)
三.四种抛物线的对比
思考:
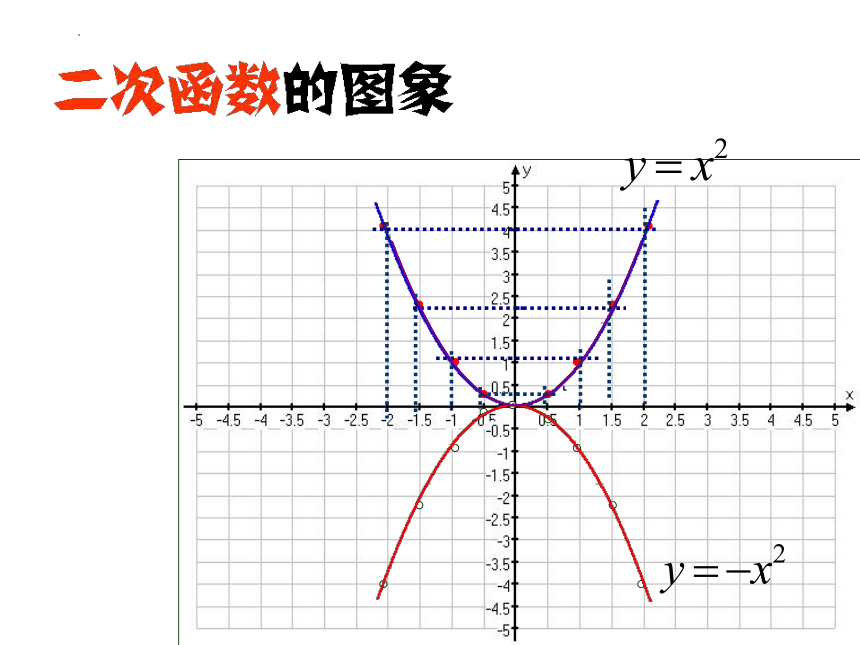
二次函数 的图像为什么是抛物线?它的焦点和准线又是什么?
例1 (1)已知抛物线的标准方程是y2 = 6x,
求它的焦点坐标和准线方程;
解: ∵2P=6,∴P=3
所以抛物线的焦点坐标是( ,0)
准线方程是x=
是一次项系数的
是一次项系数的
的相反数
(2)已知抛物线的焦点坐标是F(0,-2)
求它的标准方程。
解: 因为焦点在y的负半轴上,
所以设所求的标准方程为x2= -2py
由题意得 ,即p=4
∴所求的标准方程为x2= -8y
变式:根据下列条件,写出抛物线的标准方程:
(3)焦点在直线x+3y+15=0上
(1)准线方程 是x =
(2)焦点到准线的距离是2
求下列抛物线的焦点坐标和准线方程:
(1)y2 = 20x (2)y=2x2
(3)2y2 +5x =0 (4)x2 +8y =0
焦点坐标 准线方程
(1)
(2)
(3)
(4)
(5,0)
x= -5
(0,—)
1
8
y= - —
1
8
8
x= —
5
(- —,0)
5
8
(0,-2)
y=2
课堂练面内与一个定点F和一条定直线l(F不在l上)的距离相等的点的轨迹叫做抛物线.
定点 F 叫做抛物线的焦点,
定直线 l 叫做抛物线的准线.
图象 开口方向 标准方程 焦点 准线
向右
向左
向上
向下
﹒
y
x
o
﹒
y
x
o
y
x
o
﹒
y
x
o
﹒
谢谢!
生活中存在着各种形式的抛物线
数学这门学科不仅需要观察,还需要实验。
——欧拉抛物线的形成.gsp
平面内与一个定点F和一条定直线l
的距离相等的点的轨迹叫做抛物线。
一、抛物线的定义
定点F叫做抛物线的焦点。
定直线l 叫做抛物线的准线。
若定点F在定直线l上,M的轨迹又是什么?
F
l
·
l
F
M
N
注意:定点F在定直线l外
仿照求椭圆、双曲线标准方程的方法,如何求抛物线的标准方程?
如何建系呢?
l
解:以过F且垂直于 l 的直线为x轴,垂足为K.以F,K的中点O为坐标原点建立直角坐标系xoy.
两边平方,整理得
x
K
y
o
M(x,y)
F
二、标准方程的推导
把方程 y2 = 2px (p>0)叫做抛物线的标准方程.其中 p 为正常数.
且p 的几何意义是:
焦点坐标是:
准线方程为:
焦点到准线的距离
想一想: 在建立椭圆、双曲线的标准方程时,选择不同的坐标系得到了不同形式的标准方程,那么,抛物线的标准方程有哪些不同的形式?
﹒
y
x
o
(1)
﹒
y
x
o
(2)
﹒
y
x
o
(3)
﹒
y
x
o
(4)
y2=-2px
(p>0)
x2=2py
(p>0)
准线方程
焦点坐标
标准方程
图 形
x
F
O
y
l
x
F
O
y
l
x
F
O
y
l
x
F
O
y
l
y2=2px
(p>0)
x2=-2py
(p>0)
P的意义:抛物线的焦点到准线的距离
方程的特点:
(1)左边是二次项,且系数为1
(2)右边是一次式;决定了焦点的位置和开口方向(看一次项系数的正负)
三.四种抛物线的对比
思考:
二次函数 的图像为什么是抛物线?它的焦点和准线又是什么?
例1 (1)已知抛物线的标准方程是y2 = 6x,
求它的焦点坐标和准线方程;
解: ∵2P=6,∴P=3
所以抛物线的焦点坐标是( ,0)
准线方程是x=
是一次项系数的
是一次项系数的
的相反数
(2)已知抛物线的焦点坐标是F(0,-2)
求它的标准方程。
解: 因为焦点在y的负半轴上,
所以设所求的标准方程为x2= -2py
由题意得 ,即p=4
∴所求的标准方程为x2= -8y
变式:根据下列条件,写出抛物线的标准方程:
(3)焦点在直线x+3y+15=0上
(1)准线方程 是x =
(2)焦点到准线的距离是2
求下列抛物线的焦点坐标和准线方程:
(1)y2 = 20x (2)y=2x2
(3)2y2 +5x =0 (4)x2 +8y =0
焦点坐标 准线方程
(1)
(2)
(3)
(4)
(5,0)
x= -5
(0,—)
1
8
y= - —
1
8
8
x= —
5
(- —,0)
5
8
(0,-2)
y=2
课堂练面内与一个定点F和一条定直线l(F不在l上)的距离相等的点的轨迹叫做抛物线.
定点 F 叫做抛物线的焦点,
定直线 l 叫做抛物线的准线.
图象 开口方向 标准方程 焦点 准线
向右
向左
向上
向下
﹒
y
x
o
﹒
y
x
o
y
x
o
﹒
y
x
o
﹒
谢谢!
