青岛版(五四制)数学五年级上册 7.1 比的意义和基本性质 课件(20张PPT)
文档属性
| 名称 | 青岛版(五四制)数学五年级上册 7.1 比的意义和基本性质 课件(20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版(五四制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-05 20:28:43 | ||
图片预览








文档简介
(共20张PPT)
比
第1课时
解决下面各题。
1.六(1)班有男生25人,女生20人。男生人数是女生人数的几倍?
女生人数是男生人数的几分之几?
2.小明一家去离家160 km的游乐场,2小时到达,开车的速度是多少?
3.妈妈买了10 kg苹果,花了70元钱,每千克苹果多少钱?
从图中,你知道了哪些数学信息?根据这些信息,你能提出什么问题?
分析:
赵凡的头部长和身长有怎样的关系呢?
头部长:25cm
方法一:(相除关系)
身长:160cm
表示头部长是身长的 。
表示身长是头部长的 。
分析:
赵凡的头部长和身长有怎样的关系呢?
头部长:25cm
方法二:(相比关系)
身长:160cm
头部长和身长的比是25比160,
身长和头部长的比是160比25,
记作:
记作:
25 ∶ 160
前项
比号
后项
25
160
前项
比号
后项
“∶”是比号,读作“比”。
比号前面的数叫作比的前项,
比号后面的数叫作比的后项。
分析:
赵凡3分钟走了330米,她的行走速度是多少?
速度=路程÷时间
330米
3分钟
= 330÷3=110(米/分)
路程和时间的关系还可以用比来表示:
赵凡行走的路程和时间的比是 330∶3。
两个数相除又叫作两个数的比。
比的前项除以后项所得的商叫作比值。
比值通常用分数
表示,也可以用
小数或整数表示。
前项
比号
后项
比值
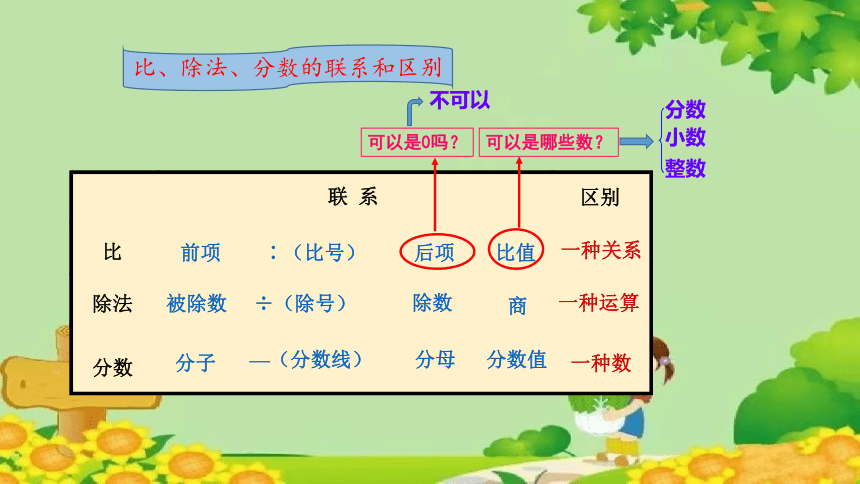
比
除法
分数
联 系
前项
被除数
分子
∶(比号)
÷(除号)
—(分数线)
后项
除数
分母
比值
商
分数值
区别
一种关系
一种运算
一种数
可以是0吗?
可以是哪些数?
分数
小数
整数
比、除法、分数的联系和区别
不可以
分析:
想一想,比有怎样的性质?
根据商不变的性质和分数的基本性质猜想:
比的前项和后项同时乘或除以相同的数,比值应该不变。
举例验证:
3 ∶ 5 =0.6
(3×2)∶(5×2)=0.6
(3×5)∶(5×5)=0.6
18 ∶ 24 =0.75
(18÷2)∶(24÷2)=0.75
(18÷3)∶(24÷3)=0.75
同时乘相同的数
比值
不变
同时除以相同的数
比值
不变
3 ∶ 5 =0.6
(3×2)∶(5×2)=0.6
(3×5)∶(5×5)=0.6
(18÷2)∶(24÷2)=0.75
(18÷3)∶(24÷3)=0.75
同时乘相同的数
比值
不变
同时除以相同的数
比值
不变
18 ∶ 24 =0.75
比的前项和后项同时乘或除以相同的数(0除外),
比值不变。这是比的基本性质。
根据比的基本性质,可以把比化成最简单的整数比。
最简单的整数比的前项和后项都是整数,而且前项和后项只有公因数1
比的相关概念
比、分数和除法的联系与区别
比的基本性质
1.观察下图,写出几个比,并说出它们表示的意义。
7.5∶10
10∶7.5
17.5∶7.5
7.5∶17.5
17.5∶10
10∶7.5
表示手指长与掌心长的关系
表示手指长与手掌长的关系
表示掌心长与手掌长的关系
2.谁快?
规范解答:
马拉松选手:
骑车人:
路程∶时间=40∶2
路程∶时间=45∶3
40∶2
45∶3
速度=路程÷时间
速度为:40÷2=20(千米/时)
20千米/时
速度为:45÷3=15(千米/时)
15千米/时
20>15,所以马拉松选手快。
规范解答:
把 4∶7 的前项增加12,要使比值不变,后项应该增加多少?
前项增加12
前项为:4+12=16
相当于变为原来的:16÷4=4倍
要使比值不变
后项变为原来的4倍
后项为:7×4=28
后项增加:28-7=21
1.填空。
3:2
2:3
20:5
4
单价
5:2
1:9
2.人体每天需要的水分约为2500毫升,其中从食物中摄取的约为1200毫升,直接饮入的约为1300毫升。写出从食物中摄取的和直接饮入的水量的比,并化简。
1200∶1300
=(1200÷100)∶(1300÷100)
答:从食物中摄取的和直接饮入的水量的比是1200∶1300,化简后是12∶13。
= 12∶13
根据比的基本性质可以将
比化成最简单的整数比。
谢 谢 大 家
比
第1课时
解决下面各题。
1.六(1)班有男生25人,女生20人。男生人数是女生人数的几倍?
女生人数是男生人数的几分之几?
2.小明一家去离家160 km的游乐场,2小时到达,开车的速度是多少?
3.妈妈买了10 kg苹果,花了70元钱,每千克苹果多少钱?
从图中,你知道了哪些数学信息?根据这些信息,你能提出什么问题?
分析:
赵凡的头部长和身长有怎样的关系呢?
头部长:25cm
方法一:(相除关系)
身长:160cm
表示头部长是身长的 。
表示身长是头部长的 。
分析:
赵凡的头部长和身长有怎样的关系呢?
头部长:25cm
方法二:(相比关系)
身长:160cm
头部长和身长的比是25比160,
身长和头部长的比是160比25,
记作:
记作:
25 ∶ 160
前项
比号
后项
25
160
前项
比号
后项
“∶”是比号,读作“比”。
比号前面的数叫作比的前项,
比号后面的数叫作比的后项。
分析:
赵凡3分钟走了330米,她的行走速度是多少?
速度=路程÷时间
330米
3分钟
= 330÷3=110(米/分)
路程和时间的关系还可以用比来表示:
赵凡行走的路程和时间的比是 330∶3。
两个数相除又叫作两个数的比。
比的前项除以后项所得的商叫作比值。
比值通常用分数
表示,也可以用
小数或整数表示。
前项
比号
后项
比值
比
除法
分数
联 系
前项
被除数
分子
∶(比号)
÷(除号)
—(分数线)
后项
除数
分母
比值
商
分数值
区别
一种关系
一种运算
一种数
可以是0吗?
可以是哪些数?
分数
小数
整数
比、除法、分数的联系和区别
不可以
分析:
想一想,比有怎样的性质?
根据商不变的性质和分数的基本性质猜想:
比的前项和后项同时乘或除以相同的数,比值应该不变。
举例验证:
3 ∶ 5 =0.6
(3×2)∶(5×2)=0.6
(3×5)∶(5×5)=0.6
18 ∶ 24 =0.75
(18÷2)∶(24÷2)=0.75
(18÷3)∶(24÷3)=0.75
同时乘相同的数
比值
不变
同时除以相同的数
比值
不变
3 ∶ 5 =0.6
(3×2)∶(5×2)=0.6
(3×5)∶(5×5)=0.6
(18÷2)∶(24÷2)=0.75
(18÷3)∶(24÷3)=0.75
同时乘相同的数
比值
不变
同时除以相同的数
比值
不变
18 ∶ 24 =0.75
比的前项和后项同时乘或除以相同的数(0除外),
比值不变。这是比的基本性质。
根据比的基本性质,可以把比化成最简单的整数比。
最简单的整数比的前项和后项都是整数,而且前项和后项只有公因数1
比的相关概念
比、分数和除法的联系与区别
比的基本性质
1.观察下图,写出几个比,并说出它们表示的意义。
7.5∶10
10∶7.5
17.5∶7.5
7.5∶17.5
17.5∶10
10∶7.5
表示手指长与掌心长的关系
表示手指长与手掌长的关系
表示掌心长与手掌长的关系
2.谁快?
规范解答:
马拉松选手:
骑车人:
路程∶时间=40∶2
路程∶时间=45∶3
40∶2
45∶3
速度=路程÷时间
速度为:40÷2=20(千米/时)
20千米/时
速度为:45÷3=15(千米/时)
15千米/时
20>15,所以马拉松选手快。
规范解答:
把 4∶7 的前项增加12,要使比值不变,后项应该增加多少?
前项增加12
前项为:4+12=16
相当于变为原来的:16÷4=4倍
要使比值不变
后项变为原来的4倍
后项为:7×4=28
后项增加:28-7=21
1.填空。
3:2
2:3
20:5
4
单价
5:2
1:9
2.人体每天需要的水分约为2500毫升,其中从食物中摄取的约为1200毫升,直接饮入的约为1300毫升。写出从食物中摄取的和直接饮入的水量的比,并化简。
1200∶1300
=(1200÷100)∶(1300÷100)
答:从食物中摄取的和直接饮入的水量的比是1200∶1300,化简后是12∶13。
= 12∶13
根据比的基本性质可以将
比化成最简单的整数比。
谢 谢 大 家
