双曲线课件
图片预览




文档简介
课件12张PPT。2.3.2双曲线的简单几何性质F1 ( -c, 0) F2 (c, 0) 温故知新一、双曲线的定义二、双曲线的标准方程F1(0, - c) F2(0, c) 我们把平面内与两个定点F1、F2的距离的差的绝对值等于常数(小于|F1F2|)的点的轨迹叫做双曲线.这两个定点叫做双曲线的焦点,两焦点的距离叫做双曲线的焦距类比椭圆的几何性质,你认为研究双曲线的哪些性质呢?活动任务分配:
1、探讨双曲线的范围
2、探讨双曲线的对称性
3、探讨双曲线的顶点
4、探讨双曲线的离心率
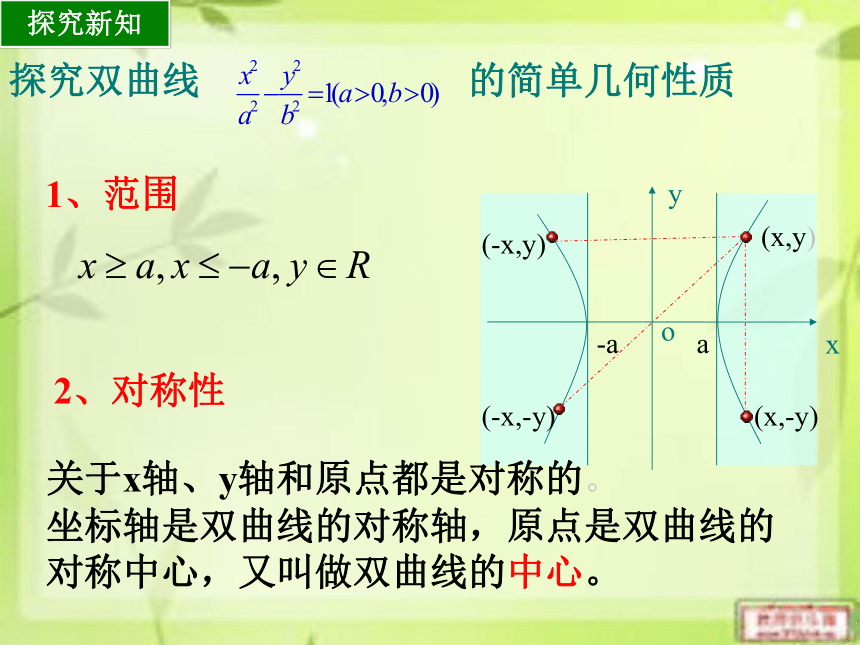
2、对称性 探究双曲线 的简单几何性质1、范围关于x轴、y轴和原点都是对称的。坐标轴是双曲线的对称轴,原点是双曲线的
对称中心,又叫做双曲线的中心。(-x,-y)(-x,y)(x,y)(x,-y)探究新知 3、顶点(1)双曲线与对称轴的交点,叫做双曲线的顶点线段 叫做双曲线的虚轴,它的长为2b,b叫做双曲线的半虚轴长4、离心率离心率。c>a>0e >1(1)定义:(2)e的范围:(3)双曲线中的基本量e是表示双曲线开口大小的一个量,e越大开口越大5、渐近线M的横坐标愈大,点就
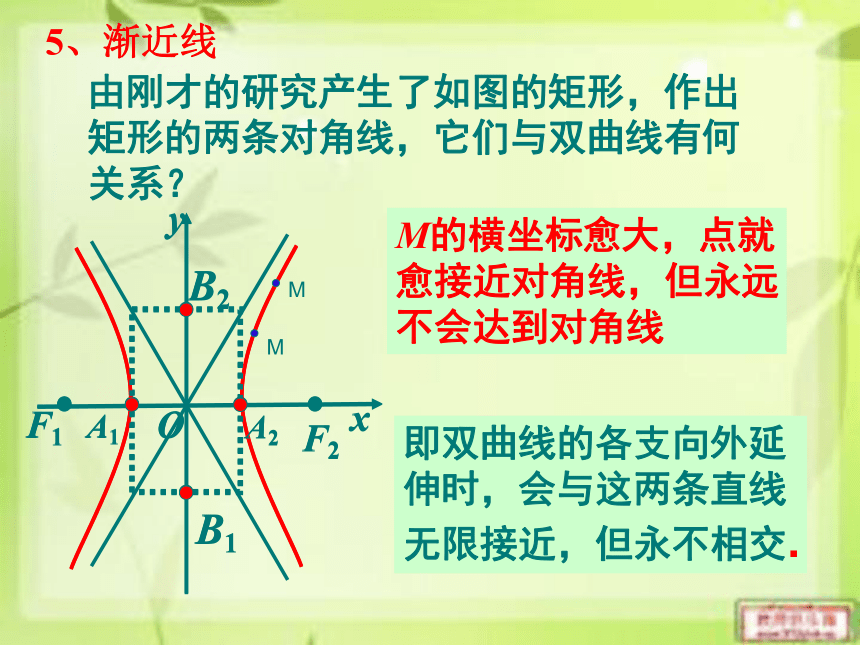
愈接近对角线,但永远
不会达到对角线即双曲线的各支向外延
伸时,会与这两条直线
无限接近,但永不相交.由刚才的研究产生了如图的矩形,作出
矩形的两条对角线,它们与双曲线有何
关系?5、渐近线这两条对角线称为双曲线的渐近线即:双曲线的渐进线方程是:(0,-a) (0, a)
(-a, 0) (a, 0)
x≤-a或x≥a
y≤-a或y≥a关于坐标轴、原点对称探究新知 例1 :求双曲线的实半轴长,虚半轴长,焦点坐标,离心率.渐近线方程。解:把方程化为标准方程可得:实半轴长a=4虚半轴长b=3半焦距c=
焦点坐标是(0,-5),(0,5)离心率:渐近线方程:应用新知下一页双曲线与椭圆简单几何性质的异同关于x轴、y轴、原点对称图形方程范围对称性顶点离心率A1(- a,0),A2(a,0)B1(0,-b),B2(0,b)F1(-c,0) F2(c,0)关于x轴、y轴、原点对称A1(- a,0),A2(a,0)渐进线无总结提升总结1. 通过类比椭圆学习了双曲线的简单几何性质:范围、对称性、顶点、离心率,并且感双曲线与渐近线的关系。2.渐近线是双曲线特有的性质,其发现与给出过程蕴含了重要的数学方法.
3.渗透了类比、数形结合等重要的数学思想.
作业布置1.巩固训练:
课本习题2.3 A组第3、4题.
2.课外拓展:
已知双曲线的焦点在y轴上,焦距为16,__________,求双曲线的标准方程(在横线上填上一个条件,并做出相应解答.)
1、探讨双曲线的范围
2、探讨双曲线的对称性
3、探讨双曲线的顶点
4、探讨双曲线的离心率
2、对称性 探究双曲线 的简单几何性质1、范围关于x轴、y轴和原点都是对称的。坐标轴是双曲线的对称轴,原点是双曲线的
对称中心,又叫做双曲线的中心。(-x,-y)(-x,y)(x,y)(x,-y)探究新知 3、顶点(1)双曲线与对称轴的交点,叫做双曲线的顶点线段 叫做双曲线的虚轴,它的长为2b,b叫做双曲线的半虚轴长4、离心率离心率。c>a>0e >1(1)定义:(2)e的范围:(3)双曲线中的基本量e是表示双曲线开口大小的一个量,e越大开口越大5、渐近线M的横坐标愈大,点就
愈接近对角线,但永远
不会达到对角线即双曲线的各支向外延
伸时,会与这两条直线
无限接近,但永不相交.由刚才的研究产生了如图的矩形,作出
矩形的两条对角线,它们与双曲线有何
关系?5、渐近线这两条对角线称为双曲线的渐近线即:双曲线的渐进线方程是:(0,-a) (0, a)
(-a, 0) (a, 0)
x≤-a或x≥a
y≤-a或y≥a关于坐标轴、原点对称探究新知 例1 :求双曲线的实半轴长,虚半轴长,焦点坐标,离心率.渐近线方程。解:把方程化为标准方程可得:实半轴长a=4虚半轴长b=3半焦距c=
焦点坐标是(0,-5),(0,5)离心率:渐近线方程:应用新知下一页双曲线与椭圆简单几何性质的异同关于x轴、y轴、原点对称图形方程范围对称性顶点离心率A1(- a,0),A2(a,0)B1(0,-b),B2(0,b)F1(-c,0) F2(c,0)关于x轴、y轴、原点对称A1(- a,0),A2(a,0)渐进线无总结提升总结1. 通过类比椭圆学习了双曲线的简单几何性质:范围、对称性、顶点、离心率,并且感双曲线与渐近线的关系。2.渐近线是双曲线特有的性质,其发现与给出过程蕴含了重要的数学方法.
3.渗透了类比、数形结合等重要的数学思想.
作业布置1.巩固训练:
课本习题2.3 A组第3、4题.
2.课外拓展:
已知双曲线的焦点在y轴上,焦距为16,__________,求双曲线的标准方程(在横线上填上一个条件,并做出相应解答.)
